2. 浙江大学 医学院 附属第二医院, 杭州 310019
2. The Second Affiliated Hospital, School of Medicine, Zhejiang University, Hangzhou 310019, China
心电图(ECG)在临床中被用于生理信号的常规监测, 是心脏电活动的图形表示, 产生的信号由多个心跳组成, 每个心跳都包含几个连续的波. 专业人员可对此进行如心肌梗死(MI)、房颤(AF)和心力衰竭(HF)[1]等多类心脏疾病的诊断, 但评估不规则ECG信号通常是耗时且主观的过程[2]. 因此, 在过去的几十年中, 计算机辅助诊断技术已被广泛应用于自动识别心律不齐的分类中[3].
早期的研究主要针对的是传统机器学习方法, 主要分为特征提取和分类器两部分, 特征提取包括均值、主成分分析[4]、傅立叶变换、小波变换[5-7]等, 分类器则主要采用SVM[2, 5]、随机森林[8]、神经网络[9, 10]等. 传统方法具有可解释性的优点, 但相对自学能力较弱, 通常无法学习潜在的抽象模式, 需要足够的人工干预, 在特征提取和特征选择上花费大量时间. 同时面对现实中的噪声和个体差异问题, 其泛化能力较弱.
为了解决以上的这些问题, 近些年, 一些学者提出了基于深度学习的方法. 与传统方法不同, 深度神经网络(DNNs)是由多个处理层组成的计算模型, 在不需要通过大量的数据预处理、特征工程的基础上, 将原始数据通过逐层抽象后得到更高层次的特征表达, 从而极大地提高模型的分类精度. 在足够充分的训练样本的前提下, 克服了传统机器学习算法输入输出相互独立的局限性[11], 同时使模型具备更优秀的泛化性和可移植性. 深度学习的方法使基于计算机的智能决策系统的开发及其在许多领域的实施取得可观的成效, 为进一步提高ECG自动分类的准确性和可扩展性提供了又一个机会. 近年来, 在DNNs方面进行了一些新的尝试, 例如残差块[12], 深度卷积神经网络[13], 深度残差卷积神经网络[14], 具有长短期记忆模块的RNN[15]和深度长短期记忆网络[16]等. 为了有效地选择特征信息并增强模型的可解释性, 注意力机制在心律失常的分类中得到了重视[17, 18]. 但是, 提高临床应用中的分类准确性还有很长的路要走.
本文提出了一种基于多头注意力机制的房颤检测算法, 对正常类(N)、房颤类(A)、其他类(O)和噪声类(~)4个类别进行分类, 模型主要分成全局特征提取, 局部特征提取, 特征强化3部分. 以级联的方式, 利用深度残差网络(ResNet)和双向长短期记忆网络(Bi-LSTM), 对原始心电信号进行特征提取, 随后引入多头注意力机制, 有选择的聚焦于重点信息进行提取, 形成特征向量用于最终分类. 经过实验证明, 该模型在分类性能上有很大的提升.
2 基于多头注意力机制的房颤检测算法本文提出的端到端的模型数据流程如图1所示, 核心部分为局部特征提取、全局特征提取、特征强化3个部分. 局部特征提取部分由深度残差网络构成, 在网络层数增加的同时可以有效解决梯度弥散的问题. 由局部特征提取部分生成的特征图, 通过在全局特征提取部分的双向长短期记忆网络, 有效地融合近邻的位置信息, 并通过多空间的自主学习, 获得全局特征之间的相关性. 最后通过Softmax层进行正常类(N)、房颤类(A)、其他类(O)和噪声类(~)4个类别的分类.
2.1 局部特征提取本文提出的模型的局部特征提取部分由深度残差网络(ResNet)实现. 深层卷积神经网络中的卷积运算可以有效地从原始心电信号中提取形态特征. 当深度神经网络达到饱和状态时, 增加网络层数或神经元数量会导致网络退化, 模型性能降低. 在深层网络中引入残差块, 可以解决梯度消失和梯度爆炸的问题, 使得在训练层数更深的网络时, 具有更高的性能. 残差块的原理如图2所示. 将前面若干层的输出数据跳过多层而引入到后面数据层的输入部分. 用F(x)表示没有跳跃连接的两层网络, 则残差块可以表示为H(x)=F(x)+x, 引入x更为丰富的参考数据. 我们利用叠加的残差卷积模块来学习局部特征, 并将长序列的心电信号压缩成一个更短的局部特征向量序列.
本文根据Hannun等[19]提出的端到端的模型进行优化, 将原始心电信号输入到几个初始层中, 输出特征映射随后由16个残差块依次进行处理. 残差块有两种形式, 都包括两个一维卷积层、一个批处理规范化层、一个激活函数层、一个dropout层和一个最大池化层. 每个卷积层有32×2k卷积核, 长度为16 (k由0开始, 每经过4个残差块递增一次). 区别在于, 第2个至第16个残差块比第1个残差块多了批处理规范化层、激活函数层、dropout层3层. 该残差网络共包括了33个卷积层和16个最大池化层. 当特征图通过池大小为2的最大池化层时, 特征映射的长度将减半, 当池大小为1时, 对特征图没有任何影响, 所以在ResNet这部分中只有8层发挥了作用. 因此最终以28因子对原始输入进行下采样, 经过局部特征提取部分, 输出长度是输入长度的1/256. 每个残差块的参数如表1所示.
2.2 全局特征提取将提取的局部特征向量逐个输入到双向长短期记忆网络层(Bi-LSTM)进行全局特征提取. 经过深度残差网络从原始心电信号中提取的局部特征代表了心脏电活动的时域过程, 通常可以使用递归神经网络以参数共享的方式进行处理. RNN的一个成功实现是LSTM, 由Hochreiter等人[20]提出. 引入一个门控机制, 包括3层: 1)遗忘门, 2)输入门和3)输出门, 该机制通过对前一个时间步中的信息量的记忆, 使得整个网络在其内部状态下更容易学习序列之间的长期依赖关系[21]. 传统的LSTM模型往往忽略了未来阶段的信息, 只处理正向的数据. 与LSTM不同, 双向长短期记忆网络是一个具有输入层、两个隐层和一个输出层的递归神经网络, 正反两个LSTM层的输出合并为一个局部聚焦的全局特征向量. 从理论上讲, 利用Bi-LSTM可以充分考虑输入数据中隐藏的全局信息. Graves和Schmidhuber实验证明, 这种双向网络比单向LSTM体系结构更加有效[22]. Bi-LSTM结构如图3所示. 本文提出模型中的两个LSTM层的单元数都是128, 这意味着每个局部聚焦的全局特征向量的长度都是128.
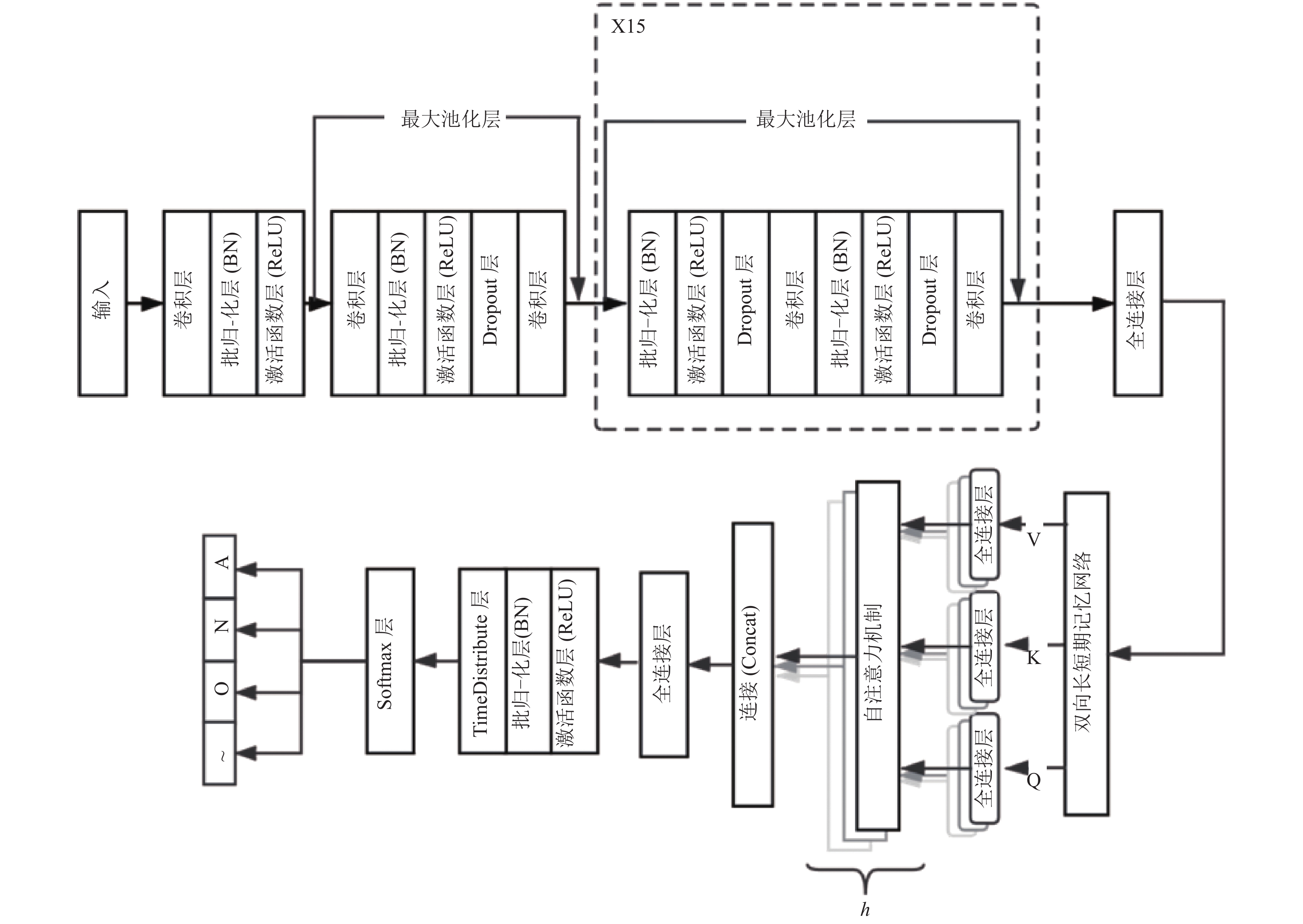
|
图 1 基于多头注意力机制的房颤检测模型 |
2.3 特征加强
注意力机制由Treisman和Gelade提出, 是一种模拟人脑注意力机制的模型. 通过计算注意力的概率分布, 来突出某个关键输入对输出的影响, 进一步捕捉序列中的重要信息, 从而优化模型并作出更为准确的判断. Bahdanau等人[23]最早将该模型应用在机器翻译任务上, 此后注意力机制就被广泛地应用到各种任务中. 注意力机制的思想核心是通过计算权重矩阵使得模型有选择的聚焦于重要信息, 他的本质是一个查询(query)到一系列键值对(key-value)的映射. 自注意力机制(self-attention)仅关注自身并从中抽取相关信息, 而不需要借助其他额外的信息, 即注意力发生在数据源内部元素之间. Q、K、V均为双向长短期记忆网络输出的特征值, 分别输入不同的全连接层获得学习矩阵, 随后将Q映射到一系列K, 即计算Q和K之间的相似度作为权重. 使用Softmax函数对权重进行归一化并最终获得权重与V的加权和. 自注意力如式(1)所示.

|
图 2 残差块结构 |
| 表 1 残差块参数 |

|
图 3 双向长短期记忆网络结构 |
多头自注意力机制的原理是将Q、K、V映射到不同的子空间中, 各个空间各自进行自注意力计算, 互不干扰, 最后将各个子空间的输出拼接在一起, 从而使模型能够捕获序列中更多的上下文信息, 进一步提高特征表达能力. 同时作为一个集成的作用, 可以防止过拟合. 多头自注意力机制如式(2)所示. 每个注意力机制函数只负责最终输出序列中一个子空间, 本文提出的最优模型中为heads-8, 将输入Q, K, V由原来的256维度变成了32维度, 即1/8, 各个子空间之间互相独立, 将多个空间的输出拼接后输入全连接层获得最终特征输出.
每一个头中的自注意力机制被定义为:
| $\begin{split} {{hea}}{{{d}}_{{i}}}& = {{Attention}}\left( {{{QW}}_{{i}}^{{Q}},{{KW}}_{{i}}^{{K}},{{VW}}_{{i}}^{{V}}} \right)\\ & = {{Softmax}}\left[ {\frac{{{{QW}}_{{i}}^{{Q}}{{\left( {{{KW}}_{{i}}^{{K}}} \right)}^{\rm{T}}}}}{{\sqrt {{{{d}}_{{k}}}} }}} \right]{{VW}}_{{i}}^{{V}} \end{split}$ | (1) |
其中,
| $\begin{array}{l} {{MultiHead}}\left( {{{Q}},{{K}},{{V}}} \right)= {{Concat}}\left( {{{hea}}{{{d}}_1},{{hea}}{{{d}}_2}, \cdots ,{{hea}}{{{d}}_{{h}}}} \right){{{W}}^{{o}}} \end{array}$ | (2) |
其中, Q, K, V是输入的心电信号矩阵,
由于Softmax函数的性质, 当输入值极大时, 该函数将落在梯度极小的地方. 因此, 比例因子
我们将PhysioNet 2017挑战赛的公开数据集[24]应用于模型的训练和测试, 该心电信号数据集包含4个心律类别: 正常类(N)、房颤类(A)、其他类(O)和噪声类(~)4类. 2017年PhysioNet挑战赛公开数据集的数据格式如表2所示. 该数据集由8528个单导ECG数据记录组成, 每个记录都以300 Hz的频率采样, 长度约为9~61 s.
3.2 评价标准实验分别将精度(precision), 召回率(recall), F1得分(F1)、准确率(accuracy)作为评估所提出模型的性能的标准.
| $ {{precision}} = \frac{{{{TP}}}}{{{{TP}} + {{FP}}}}$ | (3) |
| $ recall=\frac{TP}{TP+FN} $ | (4) |
| ${{F}}1 = \frac{{2{{*precision*recall}}}}{{{{precision}} + {{recall}}}}$ | (5) |
| $ accuracy=\frac{TP+TN}{TP+TN+FP+FN} $ | (6) |
其中, TP为真阳性, TN为真阴性, FP为假阳性, 而FN为假阴性.
| 表 2 2017年PhysioNet挑战赛公开数据集 |
3.3 实验设置
批量归一化用于确保每个卷积层之前网络的平滑收敛. 同时, 使用ReLU激活函数可以有效地提高网络的学习效率, 并显著的减少深度学习网络中收敛所需的迭代次数. 交叉熵函数用于评估输出标签和参考标签之间的差异, 如式(7)所示. 交叉熵的值越小, 实际输出和预期输出的分布越紧密. 根据交叉熵, 可以建立模型训练中的停止机制. 当交叉熵值在8个周期内都没有变化时, 模型训练将自动停止. 此外, 实验均在配备Tesla v100-sxm2 GPU的服务器中进行, 统一采用2017年挑战赛公开数据集进行训练和测试. 模型基于Python 3.6和Keras 2.1.6框架进行开发.
| ${{loss}}\left( {{{X}},{{r}}} \right) = - {\rm{log}}\frac{{{\rm{exp}}({{P}}({{X}},{{r}}))}}{{\displaystyle\sum\nolimits_{{{i}} = 0}^{{N}} {\rm{e}} {\rm{xp}}({{P}}({{X}},{{i}}))}}$ | (7) |
其中, r表示标签, 而P(X,i)是模型将标签i分配给输入X的概率.
3.4 实验结果与分析实验中所有模型的参数设置均为最佳值, 并且取结果的最优值进行比较. 为了保证实验的公平性, 所有的实验都将Adam优化器的初始学习率设置为10−2, Dropout设置为0.3. 本文中的所有实验采用2017年PhysioNet挑战赛公开数据集作为数据用于模型的训练和评估, 并将90%训练集, 10%作为测试集. 为了验证本文所提出的模型性能的优越, 进行了如下几个同类别的对比实验: 1) ResNet[19]: 吴恩达提出的34层端到端的深度残差网络模型; 2) ResNet+Bi-LSTM: 在深度残差网络的基础上加入双向长短期记忆网络; 3) CL3[25]: PhysioNet 2017参赛模型, 单层CNN结合多层LSTM模型; 4) QRS-LSTM[26]: PhysioNet 2017参赛模型, Pan-Tompkins R峰检测算法获得QRS数据结合多层LSTM. 由表3结果所示, 本文提出的基于多头注意力机制的分类模型在分类性能上优于同类模型.
| 表 3 不同模型分类结果比较 |
本文模型首先采用深度残差网络提取心电信号的局部特征, 实验ResNet结果表明, 残差块在提升模型性能上具有良好的表现. 但是该特征过于分散, 无法进行最终分类. 因此, 我们将局部特征向量序列输入到一个Bi-LSTM层中提取全局特征. Bi-LSTM善于描述时间行为, 但很难处理很长的序列. 经过局部特征学习后, 心电信号的序列长度得以压缩, 从而提高基于Bi-LSTM学习全局特征的有效性, 这就是在全局特征提取部分前加入局部特征提取部分的原因, 实验ResNet+Bi-LSTM也表明两个模块的结合性能优于单个ResNet模型的性能. Bi-LSTM某一步的输出表现为一组局部聚焦的全局特征, 特征受该步附近输入影响. 为了得到更具代表性的特征向量, 本文将Bi-LSTM层的输出传入多头注意力机制层对特征进行重点提取. 多个模块通过级联的方式将相连接并发挥各自模块的作用, 提升整体模型的性能.
多头注意力机制是在原始注意力机制的基础上, 将学习分散到不同子空间中, 获取更多层面的不同位置特征. 但分类性能并不是随子空间的增加而线性提升, 过多的子空间数量可能会引起过拟合, 反而会对模型的分类精度造成影响. 为此, 本文又做了3个对比实验, 对应的是heads-2, heads-4以及heads-16, 仅仅改变了本文提出模型中特征强化部分的子空间数量. 根据表3的结果显示, heads-4和heads-8指标相近, 明显优于heads-2和heads-16. 根据图4的混淆矩阵显示, heads-8对房颤类别的分类准确率高达0.93, 明显优于对比实验. 同时, 结合所有的对比实验, 可由图5发现, heads-2, heads-4, heads-16, ResNet的准确率呈现波动状, 而heads-8的准确率在所有实验中收敛的更快以及更稳定. 由此可以体现本文提出的模型在收敛性能上也有较好的表现.
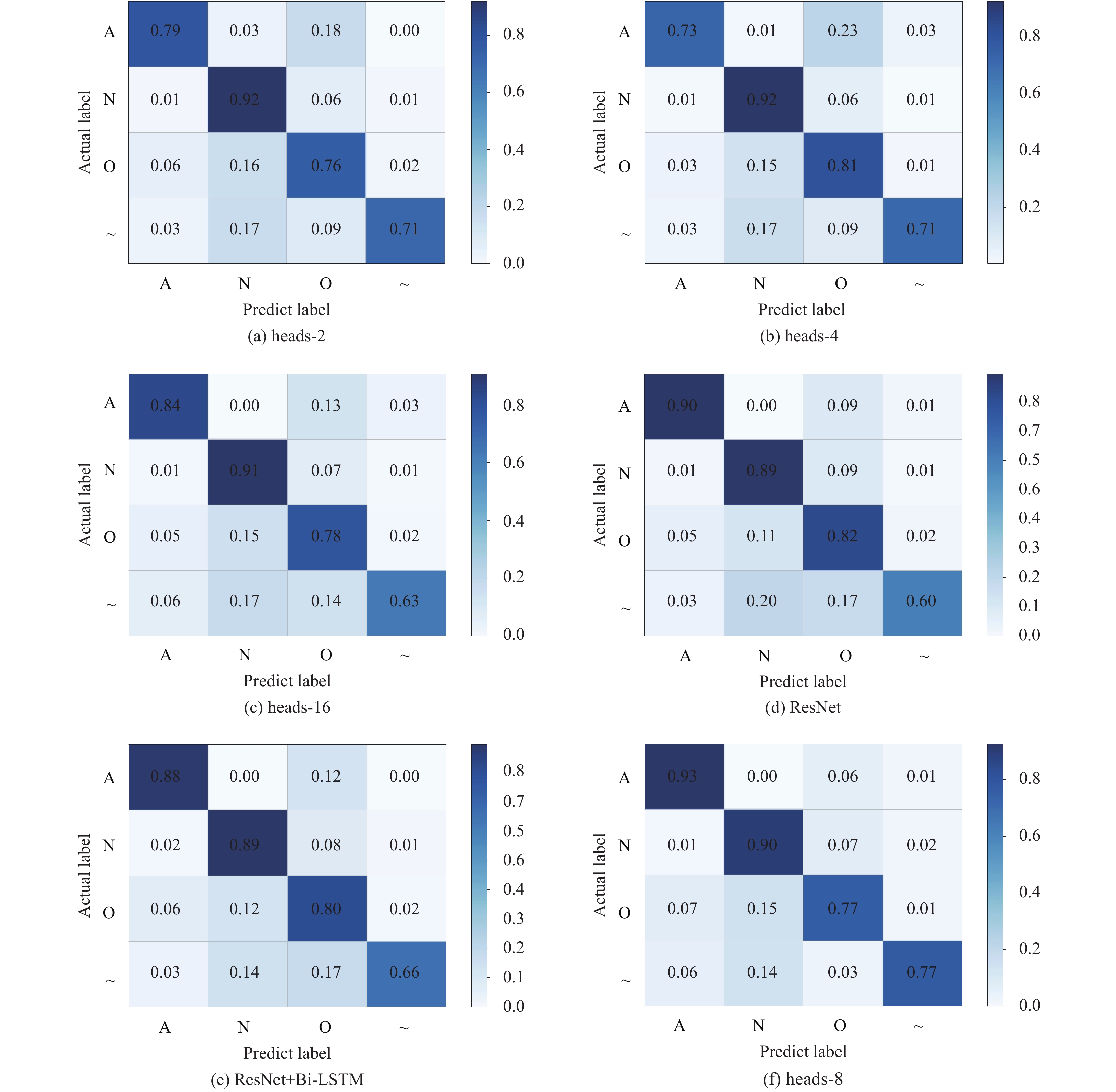
|
图 4 不同实验混淆矩阵 |
4 结论
本文提出了一种基于多头注意力机制的心律失常分类算法, 对房颤、正常、噪声、其他4类进行分类, 并通过多个实验, 验证了该网络模型的可行性. 本文算法的核心之处在于首先采用深度残差网络提取心电信号的局部特征, 然后将特征图传入双向长短期记忆网络层, 最后传入多头注意力机制层对特征进行重点提取. 但是, 这项工作的局限性在于它仅使用2017年PhysioNet挑战赛的公开数据, 并且未在其他公开数据库中进行过培训和测试, 也未应用于医院中实际患者的测量数据. 尽管优化模型为改善房颤的自动分类提供了有效的方法, 但它并不适合实际的临床诊断和实际患者的应用. 同时, 该模型中心血管疾病的分类仅限于房颤、噪声、正常和其他4个类别. 将来, 我们的目标是将模型的自动分类扩展到更广泛的疾病领域中去.

|
图 5 不同实验准确率 |
| [1] |
Turakhia MP. Moving from big data to deep learning—the case of atrial fibrillation. JAMA Cardiology, 2018, 3(5): 371-372. DOI:10.1001/jamacardio.2018.0207 |
| [2] |
Osowski S, Hoai LT, Markiewicz T. Support vector machine-based expert system for reliable heartbeat recognition. IEEE Transactions on Biomedical Engineering, 2004, 51(4): 582-589. DOI:10.1109/TBME.2004.824138 |
| [3] |
Oh SL, Ng EYK, Tan RS, et al. Automated diagnosis of arrhythmia using combination of CNN and LSTM techniques with variable length heart beats. Computers in Biology and Medicine, 2018, 102: 278-287. DOI:10.1016/j.compbiomed.2018.06.002 |
| [4] |
Martis RJ, Acharya UR, Mandana KM, et al. Cardiac decision making using higher order spectra. Biomedical Signal Processing and Control, 2013, 8(2): 193-203. DOI:10.1016/j.bspc.2012.08.004 |
| [5] |
Sahoo S, Kanungo B, Behera S, et al. Multiresolution wavelet transform based feature extraction and ECG classification to detect cardiac abnormalities. Measurement, 2017, 108: 55-66. DOI:10.1016/j.measurement.2017.05.022 |
| [6] |
Thomas M, Das MK, Ari S. Automatic ECG arrhythmia classification using dual tree complex wavelet based features. AEU-International Journal of Electronics and Communications, 2015, 69(4): 715-721. DOI:10.1016/j.aeue.2014.12.013 |
| [7] |
Elhaj FA, Salim N, Harris AR, et al. Arrhythmia recognition and classification using combined linear and nonlinear features of ECG signals. Computer Methods and Programs in Biomedicine, 2016, 127: 52-63. DOI:10.1016/j.cmpb.2015.12.024 |
| [8] |
Li TY, Zhou M. ECG classification using wavelet packet entropy and random forests. Entropy, 2016, 18(8): 285. DOI:10.3390/e18080285 |
| [9] |
Melin P, Amezcua J, Valdez F, et al. A new neural network model based on the LVQ algorithm for multi-class classification of arrhythmias. Information Sciences, 2014, 279: 483-497. DOI:10.1016/j.ins.2014.04.003 |
| [10] |
Martis RJ, Acharya UR, Lim CM, et al. Application of higher order cumulant features for cardiac health diagnosis using ECG signals. International Journal of Neural Systems, 2013, 23(4): 1350014. DOI:10.1142/S0129065713500147 |
| [11] |
Schmidhuber J. Deep learning in neural networks: An overview. Neural Networks, 2015, 61: 85-117. DOI:10.1016/j.neunet.2014.09.003 |
| [12] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV, USA. 2016. 770–778.
|
| [13] |
Wu Q, Sun YF, Yan H, et al. ECG signal classification with binarized convolutional neural network. Computers in Biology and Medicine, 2020, 121: 103800. DOI:10.1016/j.compbiomed.2020.103800 |
| [14] |
Li Z, Zhou DS, Wan L, et al. Heartbeat classification using deep residual convolutional neural network from 2-lead electrocardiogram. Journal of Electrocardiology, 2020, 58: 105-112. DOI:10.1016/j.jelectrocard.2019.11.046 |
| [15] |
Faust O, Shenfield A, Kareem M, et al. Automated detection of atrial fibrillation using long short-term memory network with RR interval signals. Computers in Biology and Medicine, 2018, 102: 327-335. DOI:10.1016/j.compbiomed.2018.07.001 |
| [16] |
Yildirim Ö. A novel wavelet sequence based on deep bidirectional LSTM network model for ECG signal classification. Computers in Biology and Medicine, 2018, 96: 189-202. DOI:10.1016/j.compbiomed.2018.03.016 |
| [17] |
Yao QH, Wang RX, Fan XM, et al. Multi-class Arrhythmia detection from 12-lead varied-length ECG using attention-based time-incremental convolutional neural network. Information Fusion, 2020, 53: 174-182. DOI:10.1016/j.inffus.2019.06.024 |
| [18] |
Zhang J, Liu AP, Gao M, et al. ECG-based multi-class arrhythmia detection using spatio-temporal attention-based convolutional recurrent neural network. Artificial Intelligence in Medicine, 2020, 106: 101856. DOI:10.1016/j.artmed.2020.101856 |
| [19] |
Hannun AY, Rajpurkar P, Haghpanahi M, et al. Cardiologist-level arrhythmia detection and classification in ambulatory electrocardiograms using a deep neural network. Nature Medicine, 2019, 25(1): 65-69. DOI:10.1038/s41591-018-0268-3 |
| [20] |
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [21] |
Tan JH, Hagiwara Y, Pang W, et al. Application of stacked convolutional and long short-term memory network for accurate identification of CAD ECG signals. Computers in Biology and Medicine, 2018, 94: 19-26. DOI:10.1016/j.compbiomed.2017.12.023 |
| [22] |
Graves A, Schmidhuber J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Networks, 2005, 18(5–6): 602-610. |
| [23] |
Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translate. arXiv: 1409.0473, 2014.
|
| [24] |
Clifford GD, Liu CY, Moody B, et al. AF classification from a short single lead ECG recording: The PhysioNet/Computing in Cardiology Challenge 2017. Proceedings of 2017 Computing in Cardiology. Rennes, France. 2017. 1–4.
|
| [25] |
Warrick P, Homsi MN. Cardiac arrhythmia detection from ECG combining convolutional and long short-term memory networks. Proceedings of 2017 Computing in Cardiology. Rennes, France. 2017. 1–4.
|
| [26] |
Maknickas V, Maknickas A. Atrial fibrillation classification using QRS complex features and LSTM. Proceedings of 2017 Computing in Cardiology. Rennes, France. 2017. 1–4.
|
 2021, Vol. 30
2021, Vol. 30



