随着“互联网+”的发展, 各种E-learning在线学习系统在教育领域中普遍应用, 海量的网络教学资源在为用户提供了便利的同时, 也出现了“认知过载”和“学习迷航”等问题. 为解决这些问题, 个性化推荐系统应运而生, 根据用户的信息需求、兴趣偏好等, 将匹配度高的资源推荐给用户. 推荐策略主要包括: 基于内容的推荐、协同过滤推荐、混合推荐、基于网络结构的推荐、基于关联规则的推荐、基于知识的推荐等[1-6]. 学习资源的推荐与电影、音乐、旅游等商品推荐的不同之处在于: 除了用户的兴趣偏好之外, 还应考虑用户的认知水平、学习目标等个性化因素, 以及知识点之间的逻辑关系.
2012年谷歌正式提出了“知识图谱”这个术语, 知识图谱旨在描述真实世界中存在的各种实体或概念, 以及他们之间的关联关系[7]. 在知识图谱中, 将每条知识表示为<实体, 实体关系, 实体>或<实体, 属性, 属性值>的三元组, 将所有数据组织成一张有向图[8]. 基于知识图谱的推荐方法大致分为基于本体(Ontology)的推荐生成和基于开放链接数据(LOD)的推荐生成两大类[7], 近年来广泛地应用在旅游推荐、电影/音乐推荐、电子商务和职位推荐等领域.
因此, 本文将知识图谱融入学习资源推荐模型, 构建语义网络, 综合考虑用户的兴趣偏好、学习资源所涵盖知识点的关联度与中心度, 建立多目标优化模型. 使用自适应多目标粒子群(AMOPSO)算法得到Pareto最优解集, 进行个性化学习资源的推荐.
1 学科知识图谱的构建本体这一概念源于哲学领域, 是对某一特定领域中共享概念模型的明确的形式化规范化说明, 包含了“概念模型”、“明确化”、“形式化”和“共享”4层含义[9]. 利用本体进行知识表示有利于呈现目标知识的逻辑关系, 查询以及共享. 在学科资源本体模型中知识点是资源描述的基本单位, 每个知识点对应多个相关的学习资源, 包括文本、图像、音视频等[8]. 将知识点作为知识图谱中的实体, 将知识点的特征作为知识点实体的属性, 以这样的规则关联到知识图谱中展开研究. 本体的构建方法和表示语言有很多种, 适用于不同的学科领域和工程应用. 本文首先抽取知识点并挖掘知识点之间的关联关系和知识点的属性, 然后根据知识点结构构建学科知识图谱.
1.1 实体抽取在学科知识图谱中将知识点作为图谱中的实体, 实体抽取即提取出教学资源中的概念、定义、定理、性质、公式等领域术语. 常用的实体抽取方法有基于规则与词典的方法、基于传统机器学习识别的方法、基于深度学习的抽取方法等[10]. 本文利用网络爬虫从指定的网页上完成对学习资源文本内容数据的抓取和保存, 使用中国科学院计算技术研究所分词工具NLPIR进行数据清洗和预处理后, 通过TF-IDF算法进行知识点的提取. TF-IDF算法采用文本逆频率IDF (Inverse Document Frequency, 逆文本频率指数)对TF (Term Frequency, 词频)值加权取权值大的作为关键词.
| $T{F_i} = \frac{{{n_{ij}}}}{{\displaystyle\sum\limits_k {{n_{kj}}} }}$ | (1) |
| $ID{F_i} = \log \frac{{\left| D \right|}}{{{\rm{1 + }}\left| {\left\{ {j:{t_i} \in {d_i}} \right\}} \right|}}$ | (2) |
| $TF - IDF = \frac{{T{F_i} \cdot \log \left( {\dfrac{{\left| N \right|}}{{1 + \left| {\left\{ {j:{t_i} \in {d_j}} \right\}} \right|}}} \right)}}{{\sqrt {\displaystyle\sum\limits_{j = 1}^n {{{\left( {T{F_i} \cdot \log \left( {\dfrac{{\left| N \right|}}{{1 + \left| {\left\{ {j:{t_i} \in {d_j}} \right\}} \right|}}} \right)} \right)}^2}} } }}$ | (3) |
其中,
关系抽取是为了解决实体间语义链接的问题. Google推出的Word2Vec通过训练将每个词映射成K维实数向量后, 可通过词之间的距离(比如余弦相似度、欧氏距离等)来判断它们之间的语义相似度, 然后在词条间建立其层次关系树. 本文中根据实际需要, 定义以下5种知识点之间的关系: 前驱关系、后继关系、包含关系、并列关系、同义关系. 具体含义如表1所示.
| 表 1 知识点间的关系定义 |
1.3 本体构建
本文以C语言程序设计课程为例, 采用斯坦福大学开发的Protégé工具进行本体的构建. 如图1.

|
图 1 课程本体部分关系示例 |
2 基于知识图谱的多目标学习资源推荐模型的构建 2.1 学习资源数学模型的建立
学习资源特征用向量
将用户特征模型表示为:
本文提出基于知识图谱的多目标学习资源推荐模型. 本模型包两个目标函数: 学习资源包含的知识点与用户知识库的距离(Resource Knowledge Distance, RKD)和用户对学习资源类型的偏好(Resource Type Preferences, RTP), 即
学习资源包含的知识点与用户知识库的距离如下:
| $ RKD(K(R),K(U))={\displaystyle \sum _{{k}_{i}\in K(R){\text{且}}{k}_{i}\notin K(U)}\frac{ShortestPath({k}_{i},K(U))}{Degree\left|{k}_{i}\right|}}$ | (4) |
其中,
如图2示例, 用户知识库
| $RKD(K({R_{\rm{1}}}),K(U)) = \frac{{ShortestPath({k_{\rm{5}}},K(U))}}{{Degree\left| {{k_5}} \right|}}$ | (5) |
| $\begin{split} RKD(K({R_{\rm{2}}}),K(U)) =& \dfrac{{ShortestPath({k_{\rm{4}}},K(U))}}{{Degree\left| {{k_{\rm{4}}}} \right|}} \\ &{\rm{+ }}\dfrac{{ShortestPath({k_{\rm{7}}},K(U))}}{{Degree\left| {{k_7}} \right|}} \end{split} $ | (6) |
| $RKD(K({R_{\rm{3}}}),K(U)) = \frac{{ShortestPath({k_{\rm{4}}},K(U))}}{{Degree\left| {{k_{\rm{4}}}} \right|}}$ | (7) |
计算后得到距离
学习资源类型与用户学习偏好之间的差异如下:
| $RTP(T(R),P(U)) = \sum\limits_{i = 1}^4 {\sqrt {{{({t_i} - {p_i})}^2}} } $ | (8) |
其中,
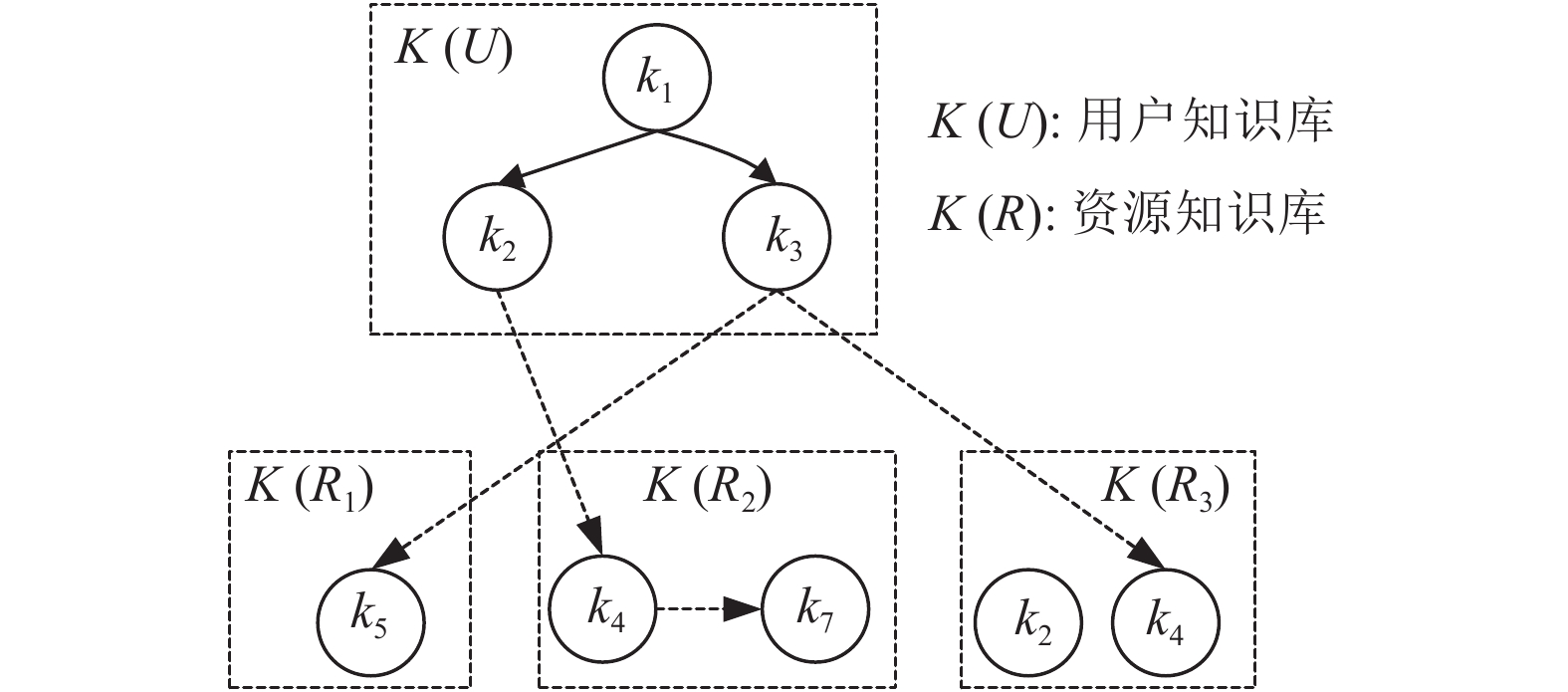
|
图 2 用户知识库与资源知识库的关系示意图 |
3 基于知识图谱的多目标学习资源推荐模型求解
个性化学习资源推荐问题是一个多目标优化问题(MOP), 本文采用自适应多目标粒子群算法(AMOPSO)进行基于Pareto非劣解集下的多目标规划. 粒子群算法(PSO)是一种模拟鸟群觅食的随机搜索算法, 能够在一次迭代过程中产生多个Pareto近似最优解, 在求解多目标优化问题上具有较强的优势. AMOPSO充分利用PSO快速收敛的优点, 兼顾避免陷入局部极值的弱点, 通过进化环境反馈信息来自适应调节粒子运动参数和极值扰动策略, 从而有效平衡开发与开采过程, 保证粒子具有很好的全局搜索能力和较快的收敛速度[12, 13].
3.1 自适应多目标粒子群算法标准多目标粒子群算法(MOPSO)迭代公式为:
| $\begin{split} {v_i}(t + 1) =& {\omega _i} \cdot {v_i}(t) + {c_1}(t){r_1}[{p_i}(t) - {x_i}(t)] \\ & + {c_2}(t){r_2}[{p_g}(t) - {x_i}(t)] \end{split} $ | (9) |
| ${x_i}(t + 1) = {x_i}(t) + {v_i}(t + 1)$ | (10) |
其中,
MOPSO有迭代初期局部搜索能力较弱、迭代后期易陷于局部最优的缺点[14]. 为了平衡MOPSO算法的全局搜索能力和局部更新能力, 自适应多目标粒子群算法(AMOPSO)采用非线性的惯性权重因子公式, 使惯性权重因子
| ${\omega _i} = \left\{ {\begin{array}{*{20}{l}} {\alpha \cdot {\omega _{\max }},{f_i} > {f_{\rm {avg1}}}} \\ {\alpha \cdot \left[{\omega _{\max }}-\dfrac{{({\omega _{\max }}-{\omega _{\min }}) \cdot ({f_{\rm {avg1}}}-{f_i})}}{{{f_{\rm {avg1}}} - {f_{\rm {avg2}}}}}\right],{f_{\rm {avg2}}}\le{f_i}\le{f_{\rm {avg1}}}} \\ {\alpha \cdot {\omega _{\min }},{f_i} < {f_{\rm {avg2}}}} \end{array}} \right.$ | (11) |
其中,
| ${c_1}(t) = {c_{1,{\rm{ini}}}} + \frac{{{c_{1,{\rm {fin}}}} - {c_{1,{\rm {ini}}}}}}{{{t_{\max }}}}*t$ | (12) |
| ${c_{\rm{2}}}(t) = {c_{{\rm{2}},{\rm {ini}}}} + \frac{{{c_{{\rm{2}},{\rm {fin}}}} - {c_{{\rm{2}},{\rm {ini}}}}}}{{{t_{\max }}}}*t$ | (13) |
其中,
以最小值
Step 1. 初始化种群和速度. 计算目标函数值并将非支配解加入外部种群存档
Step 2. 将本次迭代中内部种群中的非支配解复制至
Step 3. 更新全局最优位置.
Step 4. 根据式(11)计算自适应权重系数
Step 5. 判断是否满足终止条件, 如果达到则输出
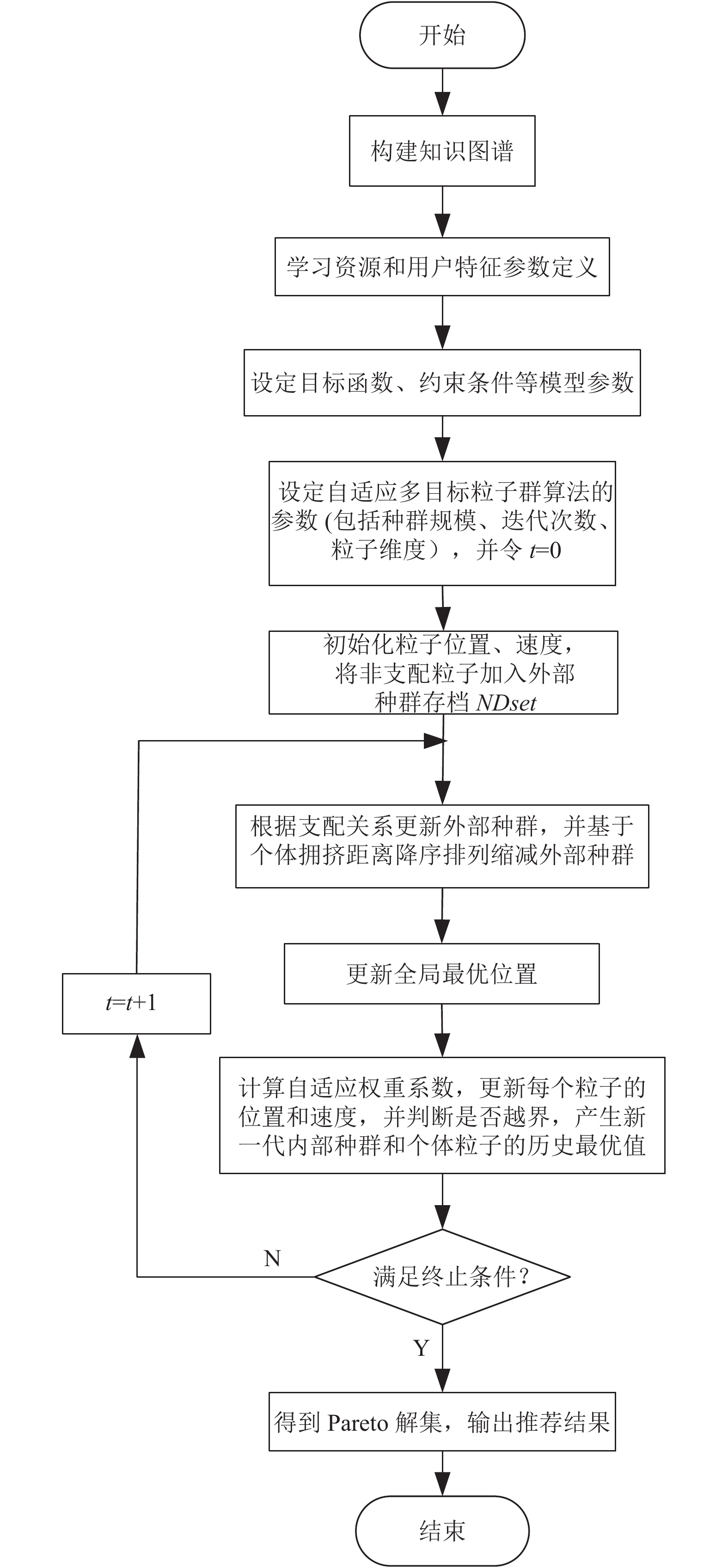
|
图 3 AMOPSO资源推荐流程图 |
4 实验与分析 4.1 实验环境与数据集
本文利用Matlab R2016a实现上述算法, 为了观测算法的有效性和可行性, 以标准MOPSO、AMOPSO做对比实验分析推荐性能的差别. 求解后从Pareto解集中选取Top-10作为推荐的学习资源; 若Pareto解集中的数据小于10条, 则选择所有的候选集作为推荐内容.
从某网络学习平台数据中爬取了部分包含C语言课程知识的文档与在线学习数据信息, 经过数据清洗和分词处理后抽取知识点和关系, 构建课程本体并经过补全形成实验数据集.
4.2 算法参数设置MOPSO和AMOPSO中特征参数的选取如表2所示.
| 表 2 算法参数设置 |
4.3 实验结果分析
为了观察推荐效果, 使用HV (Hyper Volume)值对实验结果进行分析. 由表3和图4可知, AMOPSO的HV指标最好值、均值、最差值均高于MOPSO, 说明AMOPSO的收敛性和多样性优于MOPSO; 同时AMOPSO的HV值分布范围窄于MOPSO, 说明AMOPSO的稳定性更好, 在进行学习资源推荐时的综合性能更好.
| 表 3 实验中HV值的统计结果 |

|
图 4 MOPSO和AMOPSO的HV箱线图 |
如图5所示, 使用MOPSO和AMOPSO算法分别进行资源推荐的计算可以得到两个不同的Pareto前沿面. X轴为目标函数RTP, 表示学习资源类型与用户学习偏好之间的差异; Y轴为目标函数RKD, 表示学习资源包含的知识点与用户知识库的距离. AMOPSO求得的Pareto前沿具有良好的分布特征和较好的多样性, 且收敛效果更好, 表明AMOPSO在Pareto前沿面上的寻找更有优越性, 更适合求解多目标学习资源推荐问题.

|
图 5 MOPSO和AMOPSO的Pareto前沿面 |
传统MOPSO算法采用固定惯性权重因子, AMOPSO中通过式(11)使惯性权重因子
学习因子

|
图 6 AMOPSO算法惯性权重随迭代次数变化曲线图 |
4.4 收敛性能分析
反向世代距离(Inverted Generational Distance, IGD)指标可用于评估多目标优化算法中非支配解集对真实Pareto前沿最优解集的逼近程度. IGD值越小, 表明推荐精度越高, 算法收敛性和分布性能越好[15].
| $IGD(P,Q) = \frac{1}{{\left| P \right|}}\sum\nolimits_{v \in P} {d(v,Q)} $ | (14) |
其中,
由表4可知, AMOPSO的IGD指标均值和方差均比MOPSO小, 表明AMOPSO在收敛性和分布均匀性上均优于标准MOPSO.
| 表 4 实验中IGD指标的统计结果 |
4.5 推荐效用的评价指标
本文采用五折交叉验证, 将数据集随机分为5份, 每次选取其中一份作为测试集, 另外4份作为训练集, 重复5次, 每次选取不同的训练集. 将5次实验的平均值作为推荐效用的评价指标. 对推荐算法结果的分析, 使用3个指标: 查准率(Precision, P), 召回率(Recall, R)以及F1-Score值(F):
| $\left\{ {\begin{array}{*{20}{l}} {P = \dfrac{{TP}}{{TP + FP}}} \\ {R = \dfrac{{TP}}{{TP + FN}}} \\ {F = \dfrac{{2 \times P \times R}}{{P + R}}} \end{array}} \right.$ | (15) |
其中, TP (True Positive)指推荐了且用户会使用的资源, FN (False Negative)指推荐了但用户未使用的资源, FP(False Positive)指用户喜欢但没推荐的资源, TN (True Negative)指用户不喜欢且没推荐的资源. 据上述, P反映了推荐算法的推荐水平; R反映了被推荐算法所推荐的资源占用户真正喜欢的资源的比重; F值是P和R的加权平均, 均匀地反映了推荐效果. 3个指标通常都是越高越好[15, 16].
如图7所示, AMOPSO在P、R、F值上均优于MOPSO, 说明AMOPSO算法在解决本问题时综合性能较高, 推荐效果更好.

|
图 7 评价指标条形图 |
5 结论
本文在进行学习资源推荐时基于知识图谱建立学习资源推荐模型, 综合考虑用户的兴趣偏好、用户原有的知识结构与学习资源所涵盖知识点之间的关联度, 建立多目标优化模型. 对模型求解时使用AMOPSO算法, 个体拥挤距离降序排列进行外部种群规模的缩减和全局最优值的更新, 获得了分布特征良好的两目标Pareto前沿, 输出推荐资源序列. 实验时通过与经典MOPSO算法对比并使用HV、IGD指标对模型进行评价, 验证了其多样性和稳定性, 证明了算法良好的全局寻优和收敛性能. 并采用五折交叉验证, 使用查准率、召回率以及F1-Score值验证了算法的推荐效用. 在后续工作中将进一步完善用户模型和学习资源模型, 优化推荐算法以提升学习资源推荐性能.
| [1] |
李嵩, 李书琴, 刘斌. 改进的协同过滤算法及其并行化实现. 计算机工程与设计, 2018, 39(12): 3853-3859. |
| [2] |
Chughtai MW, Selamat A, Ghani I, et al. Retracted: E-learning recommender systems based on goal-based hybrid filtering. International Journal of Distributed Sensor Networks, 2015, 2015: 252. |
| [3] |
Ng YK, Linn J. CrsRecs: A personalized course recommendation system for college students. Proceedings of the 8th International Conference on Information, Intelligence, Systems & Applications. Larnaca, Cyprus. 2017. 1–6.
|
| [4] |
张俊格. 支持个性化推荐的网络学习平台设计与实现[硕士学位论文]. 西安: 陕西师范大学, 2014.
|
| [5] |
Viktoratos I, Tsadiras A, Bassiliades N. Combining community-based knowledge with association rule mining to alleviate the cold start problem in context-aware recommender systems. Expert Systems with Application, 2018, 101: 78-90. |
| [6] |
Wu DS, Lu J, Zhang GQ. A fuzzy tree matching-based personalized E-learning recommender system. IEEE Transactions on Fuzzy Systems, 2015, 23(6): 2412-2426. DOI:10.1109/TFUZZ.2015.2426201 |
| [7] |
常亮, 张伟涛, 古天龙, 等. 知识图谱的推荐系统综述. 智能系统学报, 2019, 14(2): 207-216. |
| [8] |
黄华升. 基于知识图谱的个性化学习资源推荐研究. 软件工程, 2018, 21(10): 24-26, 23. |
| [9] |
Studer R, Benjamins VR, Fensel D. Knowledge engineering: Principles and methods. Data & Knowledge Engineering, 1998, 25(1–2): 161-197. |
| [10] |
李冬梅, 张扬, 李东远, 等. 实体关系抽取方法研究综述. 计算机研究与发展, 2020, 57(7): 1424-1448. DOI:10.7544/issn1000-1239.2020.20190358 |
| [11] |
张迪. 基于知识图谱的教学资源推荐方法研究[硕士学位论文]. 武汉: 华中师范大学, 2019.
|
| [12] |
蒙璟, 李训聿, 丁霞燕. 基于改进自适应权重多目标粒子群算法的分布式电源优化配置. 电力科学与技术学报, 2020, 35(2): 55-60, 106. |
| [13] |
唐红亮, 吴柏林, 胡旺, 等. 基于粒子群优化的地震应急物资多目标调度算法. 电子与信息学报, 2020, 42(3): 737-745. DOI:10.11999/JEIT190277 |
| [14] |
李浩君, 杨琳, 张鹏威. 基于多目标优化策略的在线学习资源推荐方法. 模式识别与人工智能, 2019, 32(4): 306-316. |
| [15] |
李浩君, 张征, 郭海东, 等. 深度学习视角下的个性化学习资源推荐方法. 现代远程教育研究, 2019, 31(4): 94-103. DOI:10.3969/j.issn.1009-5195.2019.04.011 |
| [16] |
汤伟韬, 余敦辉, 魏世伟. 融合知识图谱与用户评论的商品推荐算法. 计算机工程, 2020, 46(8): 93-100. |
 2021, Vol. 30
2021, Vol. 30



