2. 南京南瑞继保电气有限公司, 南京 211106;
3. 南京航空航天大学, 南京 210016
2. NR Electric Co. Ltd., Nanjing 211106, China;
3. Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
目前, 国内用电需求随着社会的发展而不断增长. 直流输电技术[1,2]正在朝着高电压大容量的技术方向发展, 由于国土辽阔, 对其在长距离输电、跨区域联网及调度灵活等方面有着现实需求. 电网在运行过程中, 保证换流阀等关键设备稳定运行就显得至关重要. 换流阀等关键设备在电网运行过程中会不断产生热量, 当设备的热量不断聚集, 温度就会不断上升时则会影响电网的正常运行. 电网中的换流阀等关键设备出现的故障对电力系统造成的影响也越来越大[3]. 因此, 需要对电网中关键设备检测数据进行预测, 提高工作人员对设备的感知能力, 能对关键设备未来出现的变化趋势做相应的准备. 这对电网的正常运行和提供可靠的供电具有实际意义.
由于人工在处理电网设备时会存在经验不足和误操作等客观因素, 因此对电的安全性, 稳定性和智能化的要求越来越高. 阀冷系统作为电网中冷却系统的关键设备, 以水为传导介质, 水有较高的热导性, 作为“载热体”存在, 将设备的热量传递到水介质并将热能带出, 达到物理降低设备温度的目的. 阀冷系统对高压直流系统的安全运行起着至关重要作用[4]. 阀冷系统分为内冷水系统和外冷水系统两个部分. 内冷水系统是密闭式循环具有水循环、内冷水处理等功能[5]. 内冷水系统在换流阀运行时负责可靠高效通过水带走设备运行产生的热量, 送到外冷水系统中. 外冷水系统是开放式循环, 具有水质软化净化、补水等功能[6]. 冷却塔会对内冷水管道喷淋散热, 并通过风扇对外、内冷水交换将阀内冷水系统的热量排至大气环境中, 两者共同合作完成对换流阀的持续冷却, 可以达到对阀厅整个设备进行散热的目的.
阀冷系统在降低设备温度的过程中, 其涉及的参数为出阀温度, 进阀温度, 出阀压力, 内冷水导电率. 所有参数中最核心和最关键的参数是温度, 包括了出阀温度和进阀温度. 阀冷系统中换流阀的进出阀温度在运行过程中只要维持在合理范围内, 就能够保证换流阀设备的稳定运行从而保证阀冷系统的稳定运行. 由于换流阀的出阀温度和进阀温度具有很强的相关性, 所以我们选取其中进阀温度作为整个设备运行状态的评价指标. 如果设备热量过度聚集导致换流阀的进阀温度过高, 可能会损坏相应设备. 如果这个问题长时间不能够妥善解决, 就会产生严重的安全隐患, 造成难以估计的后果. 进阀温度参数短期内有波动, 但从长期来看, 具有一定的变化趋势, 可以利用时序分析如ARIMA、SVM、GRU以及ARIMA-SVM混合等方法对进阀温度进行预测, 使运行工作人员提前预知进阀温度变化趋势.
2 相关工作时序数据本质上是反应某个或者某些随机变量随时间不断变化的趋势, 分析时序数据的核心是从这些数据里挖掘出某种规律, 并利用规律对未来进行预估[7]. 时序数据分析方法从最早提出到现在经过漫长的发展, 国内外研究学者提出了许多基于时序数据分析方法[8-11]. 时序分析方法主要有3类方法, 从最开始提出的传统的时间序列预测方法, 到将机器学习和时间序列预测结合的方法, 以及要提高预测效率的基于参数模型的在线时间序列预测方法. 无论是传统的时间序列预测方法中还是应用到时序领域的机器学习方法以及基于参数模型的在线时间序列预测方法, 目前, 没有一种单一模型能够统一地对特定的时间序列数据做出最好的预测. 因此混合模型应运而生, 混合模型受益于各个模型的多样性, 减少单一模型使用风险, 很好弥补单个模型的缺陷, 可以提升时间序列预测精度.
经典的时间序列模型包括移动平均模型(Move-Average, MA)、自回归模型(Auto-Regressive, AR)、自回归移动平均模型(Auto Regressive Moving Average, ARMA), 还有其对应的各种衍生出来的模型, 如动态自回归模型和向量化的自回归模型[12]. 而Box和Jenkins[13]提出的“Box-Jenkins方法”非常流行. 该方法有3步, 第1步对给定时间序列, 确定参数模型中适当的p, q, d值, 第2步通过最有效的方法估计出参数模型的具体值, 第3步检测模型的有效性并做出相应调整.
时间序列预测方法归根到底在本质上与基于机器学习分类中的回归分析有着许多相似之处. 机器学习中许多方法都可以应用在时间序列预测方面, 并且取得了不错的效果, 例如经典的支持向量机SVM, 贝叶斯网络BN, GRU神经网络. 随着人工神经网络的不断发展, 以及神经网络在时间序列中趋势性分析有着独特的特性, 所以有人将神经网络应用在时间序列预测上, 取得很好的效果. 进一步深度学习也被看作是实现时间序列预测的有效工具. Kim[14]直接用支持向量机来预测股票价格, 并通过对比试验来验证该方法的可行性, Gestel等提出把贝叶斯证据框架[15,16]应用到最小二乘支持向量机[17,18]应用到金融领域进行时间序列预测. Das和Ghosh将贝叶斯网络(BN)应用到气象时间序列预测, 并在后续时间做了大量的工作. 在2017年, 提出基于语义贝叶斯网络的多元气象时间序列预测网络semBnet[19]. 随着深度学习的流行, 也被看作实现时间序列预测的有效工具. 机器学习本质上是多层神经网络, 主要包括卷积神经网络(Convolutional Neural Networks, CNN)和循环神经网络(Recurrent Neural Networks, RNN)[20], 其中RNN能够解决时间序列的延续性问题. RNN可以处理整个时间序列所包含的信息, 但存在长期依赖问题, 即对长序列进行学习时, RNN会出现梯度消失和梯度爆炸问题, 无法学习到长时间跨度的关系. 为了解决这个问题, Schmidhuber 教授在1997 年提出长短期记忆网络(Long Short-Term Memory, LSTM)能够很好的解决这个问题, 默认就可以记住长期的信息, 实现长程记忆.
随着计算机技术的发展和互联网的普及, 以及数据的急速增长给传统时间序列预测方法和批处理机器学习预测方法带来了极大的挑战. 在面对大数据的时候, 传统的方法的效率低下, 因此利用在线学习方法来对时间序列数据预测成为新的趋势, 而且取得了不错的效果. 和传统批处理学习方法相比, 在线学习方法不需要处理整个数据集, 只需要处理这个新的样本, 大大节约了时间提高效率. Anava等[21]提出了基于参数模型的在线时间序列预测算法ARMA-ONS, 能够将传统的时间序列模型和在线学习有效结合起来.
3 合并单元设备状态研究此章节主要针对阀冷系统的监测数据进行筛选和提取, 并在此基础上对阀冷数据进行简单时序分析.
3.1 数据提取本文工作的数据来源于中国南方电网从2017年到2019年收集的将近两年的真实数据, 包括PWR, 出阀温度, 进阀温度, 进阀压力, 冷却水流量, 冷却水导电率等相关记录. 进一步筛选和内冷水系统有关的数据, 筛选和提取出进阀温度, 出阀温度, 进阀压力, 冷却水导电率相关数据. 因此针对这个4个指标, 从MySQL数据库混乱的原始数据里提取出来, 这就需要一些数据预处理步骤, 最后可以构建出一个适合进行时间序列分析工作的数据集.
中国南方电网的设备众多, 每个阀冷设备都有相应的监测数据, 就需要对每个阀冷设备的监测数据进行分析. 因此需要把数据按照各个设备进行划分, 并按照日期时间排列, 以保证每个设备对应数据的完整性和时序性, 最终构建出一个包含4个监测指标的数据表.
经过上面的数据预处理之后, 获得了可以进行下一步时序分析的数据集.
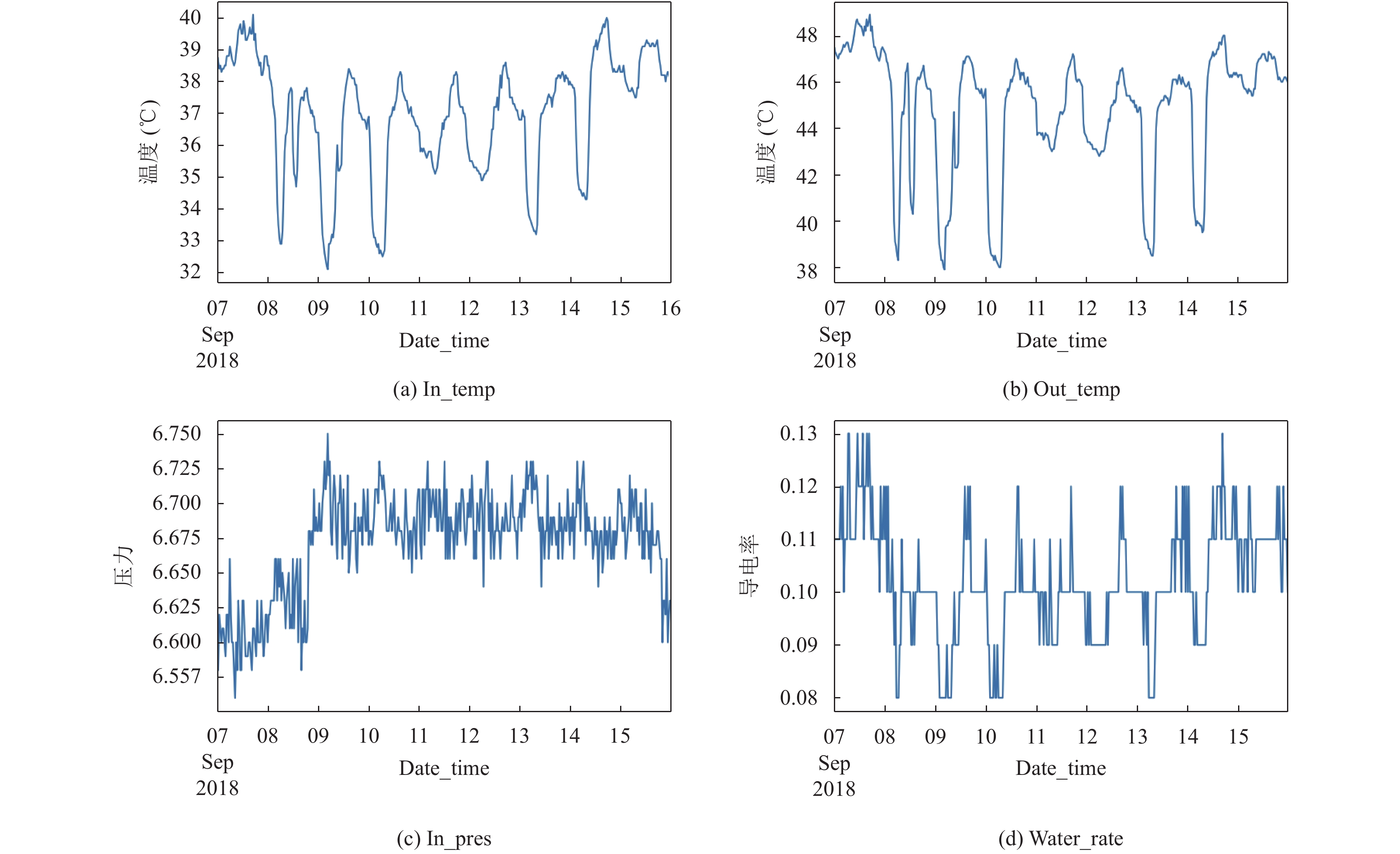
3.2 正常数据趋势分析由于整个数据的采集频率为每半个小时采集一次而且时间跨度长达两年, 导致了整个数据集比较大, 对整个数据进行趋势分析只能从宏观上观察数据变化趋势, 我们对4个指标的数据分别按周、月对数据进行采样, 分析其内在的规律性和数据的趋势变化. 对预处理的后数据集采用随机抽样, 随机选取一周的数据进行分析, 其数据随时间变化如图1所示.
图1包含了4个子图, 分别描绘了进阀温度, 出阀温度, 进阀压力, 冷却水导电率的变化趋势. 进阀温度在32℃到40℃之间变化, 相差8℃, 而出阀温度在38℃到49℃之间变化, 温度提升6℃到9℃. 进阀压力和冷却水导电率, 会随机波动, 值的波动幅度并不是很大, 且进阀压力和冷却水导电率均在正常值范围之内变化. 进阀温度, 出阀温度, 进阀压力和冷却水导电率都在某个均值附近波动, 可以初步判断各个时间序列数据是平稳的, 可以通过计算迪基-福勒检验进行单位根校验, 计算出相对应的p值为远小于0.01, 可以认为阀冷数据是时间平稳序列.
为了进一步发现阀冷变化趋势以及数据的平稳性, 我们对一个月的阀冷数据进行分析. 从图2可以看出, 进阀温度和出阀温度的变化趋势很相似, 但总体的变化范围有些不同, 进阀温度的变化范围在22℃到36℃, 而出阀温度则在24℃到42℃之间波动. 相差了2℃到6℃.
|
图 1 阀冷4个参数的周变化趋势 |

|
图 2 阀冷4个参数的月变化趋势 |
从图1和图2可以发现进阀温度在22℃到36℃的范围内变化, 出阀温度都在24℃到42℃范围内变化并且在各自对应的范围内变化趋势很是接近. 通过相关性分析得到两者关系是正相关, 相关性系数接近于1. 出阀温度和进阀温度的数据波动都在正常范围之内, 但是观察数据出阀温度略高一些, 原因在于阀冷系统的循环水将带走其产生的热量. 通过初步判断各个时间序列数据是平稳的, 再进一步通过计算迪基-福勒检验进行单位根校验, 计算出p值为远小于0.01, 最终判断阀冷数据是时间平稳序列.
4 阀冷系统的分析方法阀冷系统检测到的数据, 其具有多维度、实时性、线性和非线性并存等一些特点. 以往传统的时序分析方法是根据所研究时间序列的基本规律和自身特点, 选取适当的时序模型并先确定时间序列模型的参数, 在此基础上, 利用已求解出参数的模型对未来的时间序列进行预测. 传统时序模型在线性预测方面取得了很好的成果, 但在面对处理复杂数据的时候, 往往显得力不从心, 因此需要和基于机器学习的时间序列预测方法相结合. 与神经网络相比, SVM具有丰富的理论基础, 并且神经网络非常依赖参数,参数的好坏直接影响神经网络的学习效果. SVM可以很好弥补传统时序分析方法的缺点的同时对线性预测效果并不理想. 在对阀冷系统产生的时序数据预测, 单独的ARIMA模型或者SVM模型很难完全把握时序数据的变化规律, 考虑将二者结合起来的混合模型是个更好的解决方法, 并和神经网络GRU进行对比实验, 以验证混合模型的有效性.
在本文工作中, 我们认为阀冷时间序列
| $ {y}_{t}={L}_{t}+{N}_{t} $ | (1) |
线性部分
| $ \begin{split} {L}_{t}=&{a}_{1}{y}_{t-1}+{a}_{2}{y}_{t-2}+\dots +{a}_{p}{y}_{t-p}+{b}_{1}{\varepsilon }_{t-1}\\ &+{b}_{2}{\varepsilon }_{t-2}+\dots+{b}_{q}{\varepsilon }_{t-q}+{\varepsilon }_{q} \end{split}$ | (2) |
传统时序模型ARMA只能处理平稳时间序列, 比AR模型与MA模型有较精确的估计, 但其参数估算也相对比较繁琐. 如果是非平稳时间序列, 则难以求得ARMA模型参数的准确估值. 非平稳时间序列并不能用ARMA直接处理, 需要经过差分处理将非平稳时间序列转化成平稳时间序列. ARIMA模型在ARMA模型的基础上多了一个差分步骤, 如ARIMA(p, d, q)模型中参数d为0就是ARMA模型, 差分用参数d表示. 式(2)里线性部分
| $ AIC=2K-2\ln\left(L\right) $ | (3) |
BIC: 贝叶斯信息准则(Bayesian Information Criterion).
| $ BIC=K\ln\left(n\right)-2\ln\left(L\right) $ | (4) |
AIC准则和BIC准则用于确定ARIMA模型中p, q值. 其中, k为模型参数个数, n为样本数量, L为似然函数. 由于中国南方电网收集的阀冷数据本身就是时间平稳序列, 因此可直接建立ARIMA(p, d, q)模型中将d设为0, ARIMA中d为0其实就是ARMA模型. 首先初步确定适当的p, d, q的值, 从低阶到高阶逐步试探方法来识别模型的参数, 然后结合赤池信息度量(AIC)和贝叶斯信息度量(BIC)有效方法估计出ARIMA模型的具体参数值, 最后验证拟合模型的适当性, 并适当改进改进该模型. AIC和BIC是为了找到ARIMA模型的合适参数, 要在模型的参数个数和模型的拟合精度做出适当的取舍, 能够比较准确预测未来数据. 最终确定ARIMA模型参数p=1, d=0, q=2. ARIMA模型对线性数据具有独特的优势, 但缺点也比较明显只能捕获时间序列中线性关系, 不能捕获非线性关系. ARIMA模型在捕获线性关系过程中, 还获得线性关系之外时间序列的残差信息, 为接下来SVM分析做准备, 可以进一步优化预测值.
残差里会包括非线性关系, 而 ARIMA模型则没有办法捕获非线性的信息而支持向量机(SVM)可以捕获此类信息. 所以残差是提高预测准确性的重要因素, 因此残差分析就至关重要了. 支持向量机(SVM)在非线性预测方面能够取得很好的效果. SVM是以统计学理论为基础的学习方法, 其丰富的理论基础保证了SVM在解决数据高维度和非线性方面具有不可比拟的优势. ARIMA在捕获线性部分之外获得时间序列的残差信息, 残差即非线性部分, 残差
| $ {N}_{t}={y}_{t}-\overline{{L}_{t}} $ | (5) |
ARIMA模型在t时刻得到
| $ {\overline{N}}_{t}=g\left({N}_{t-1},{N}_{t-2},\cdots ,{N}_{t-n}\right)+{\Delta}_{t} $ | (6) |
式中, G为非线性模型, ∆t是非线性部分的随机误差, n为输入的长度. 根据以上的分析可以得到最终的预测值为:
| $ \overline{{y}_{t}}=\left\{\begin{array}{c}\overline{{L}_{t}}+\left|\overline{{N}_{t}}\right|, {N}_{t-1}>0\\ \overline{{L}_{t}}-\left|\overline{{N}_{t}}\right|, {N}_{t-1}\le 0\end{array}\right. $ | (7) |
根据数据分析结果, 我们选取、确定了ARIMA、SVM、GRU和提出的ARIMA-SVM混合时序性分析方法, 尝试建立预测模型, 对阀冷系统时序数据进行预测分析. 根据预测的结果需要评估模型的好坏, 我们采用多个度量指标来评估数据的是否平稳时间序列以及模型的准确性.
均方根误差公式表示如下:
| $ RMSE=\sqrt{\frac{1}{n}{\sum }_{i=1}^{n}({X}_{{\rm {real}},i}-{X}_{{\rm {predict}},i}{)}^{2}} $ | (8) |
均方误差公式表示如下:
| $ MSE=\frac{1}{n}\sum\nolimits_{i=1}^{n}{({x}_{{\rm {real}}, i}-{x}_{{\rm {predict}},i})}^{2} $ | (9) |
平均绝对误差表示如下:
| $ MAE=\frac{1}{n}\sum\nolimits_{j=1}^{1}\left|({x}_{{\rm {real}}, i}-{x}_{{\rm {predict}},i})\right| $ | (10) |
DF检验(Dikey-Fuller test). DF检验是一种常见的用于判断时间序列平稳性的单位根检测方法. 若通过计算不存在单位根, 时间序列就是平稳时间序列, 反之, 需要进行差分处理. 时间序列的平稳性检测是时间序列建模过程中非常重要的一步, 使用DF检测方法可以检验之.
6 实验首先我们选取中国南方电网的一个阀冷系统真实数据, 从2017年12月份到2019年7月份的真实数据中选取连续3个月的数据, 我们选取的2018年1月到3月的数据, 对这3个月的数据量进行实验分析评估, 阀冷数据采集的时间间隔为半个小时, 数据的变化趋势图2所示.
从图2中可以看到阀冷系统在平常正常工作状态中, 进阀温度, 出阀温度, 进阀压力, 冷却水导电率趋于平稳, 会产生随机波动, 但波动都在正常范围之内. 由于进阀温度比较重要, 所以我们预测输入以进阀温度为预测标准.
ARIMA模型. 第1步确定合适的p, d, q值, 在初步确定 ARIMA(p, d, q)由于阀冷数据都是时间平稳序列, 所以ARIMA模型中d=0. 第2步, 通过根据AIC和BIC检测方法确定ARIMA模型中的p和q. 第3步要检验预测数据的准确性, 拟合模型的适当性, 最终不断的适当改进模型达到准确预测数据的目的, 最终ARIMA模型参数为p=1, d=0, q=2.
实线为数据真实值, 虚线为模型在测试集上的预测. 从图3而言, ARIMA模型的进阀温度预测结果和阀冷进阀温度数据很是接近, 但在峰值区域的预测效果有些欠缺.

|
图 3 ARIMA预测图 |
SVM模型. SVM模型可以检测非线性关系, 以VC理论和结构风险最小原理为基础的, 通过选择适当的判别函数, 希望SVM的测试误差较小. 用SVM来单独预测进阀温度数据中的非线性关系.
SVM的预测性能主要和误差惩罚因子C和选取核函数有关. 优化误差惩罚因子C和核函数能够很好提升SVM的性能, 确定惩罚因子C=10, 选用径向基函数(rbf)作为核函数. C惩罚因子是确定数据子空间时调节置信区间范围. 采用遗传算法, 对两个参数优化.
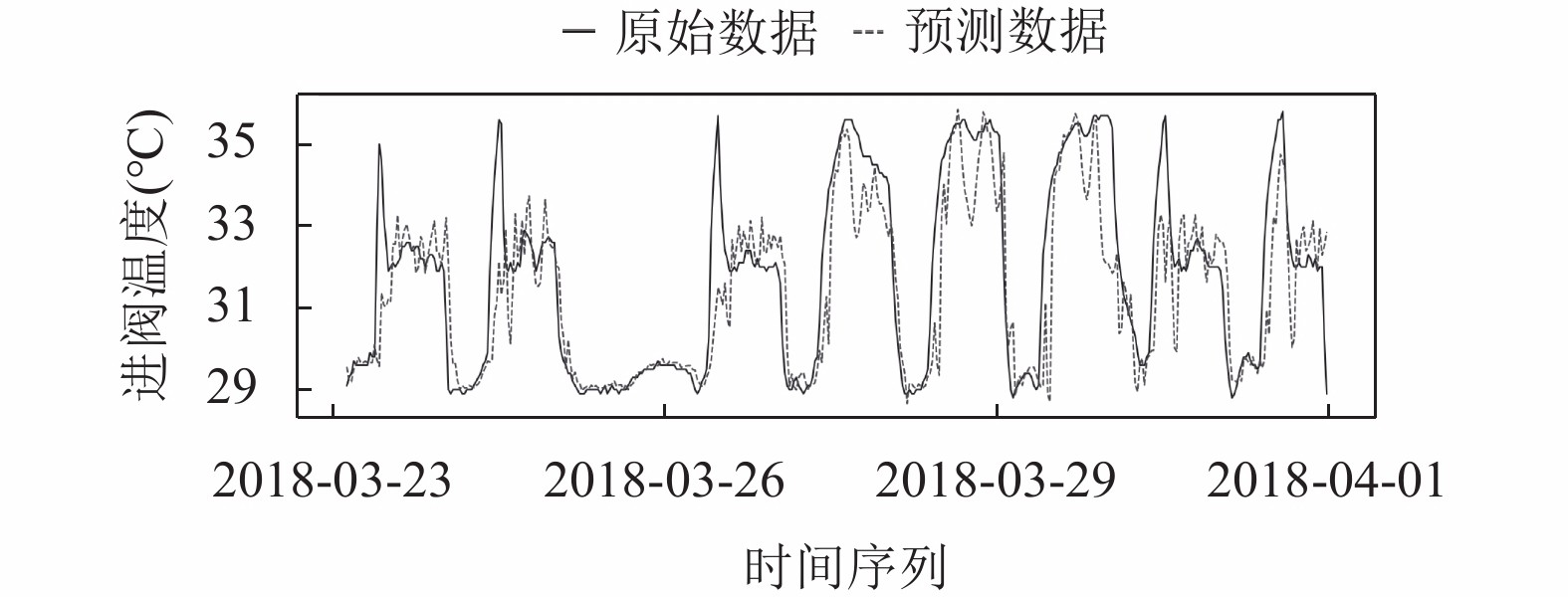
实线为数据真实值, 虚线为模型在测试集上的预测. 从图4而言, SVM模型的进阀温度预测很好拟合了真实阀冷进阀温度的变化趋势, 但是和真实进阀温度的真实值仍有差距.
|
图 4 SVM预测图 |
GRU神经网络模型. 为了进一步说明混合模型能够在单一模型的基础上提高预测精度, 将混合模型和GRU神经网络做对比实验. GRU在循环神经网络的基础上改进的变体, 引入门控机制, 自适应控制信息流动, 可以捕捉时序数据之间的相互依赖关系, 具有一定的优势. GRU神经网络模型在训练时涉及到许多超参数的设定, 神经元数量m, 时间步长T, 批数据大小batchsize, 迭代次数epoch轮. 神经元个数决定了神经网络对时序数据的拟合程度, 时间步长和批数据大小决定了模型训练的结果. 选择ADAM优化器对参数进行优化调整.
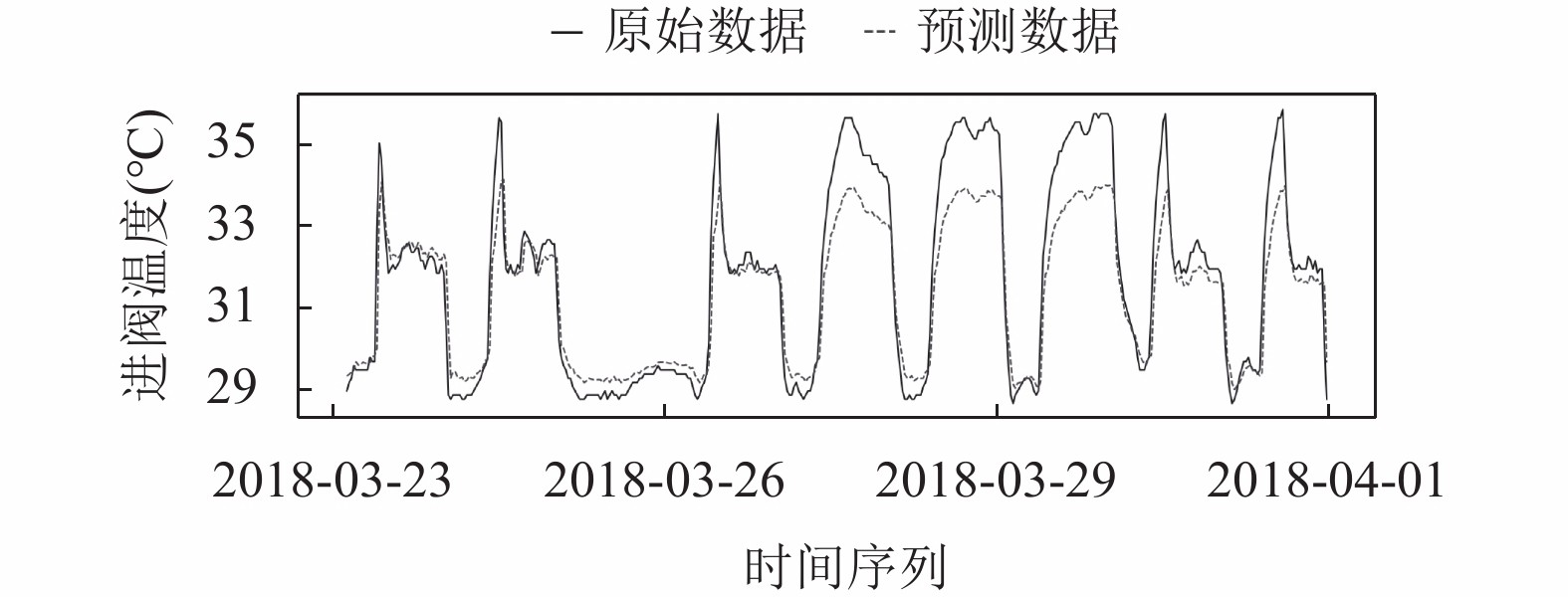
实线为数据真实值, 虚线为模型在测试集上的预测. 从图5而言, GRU模型的进阀温度预测结果比ARIMA模型预测结果更加接近真实的阀冷进阀温度数据, 在3个峰值区域的预测效果有些欠缺.
|
图 5 GRU预测图 |
ARIMA模型可以很好捕获时间序列中线性关系, 但时序数据仍有非线性关系没有捕捉. 利用SVM可以很好捕捉非线性关系, 从ARIMA获得线性关系之外时间序列的残差信息获得非线性关系. 进一步优化预测值. 从而提出ARIMA-SVM混合模型.
ARIMA-SVM混合模型结合两个模型的优点. 首先使用 ARIMA 对进阀温度时间序列进行预测, 捕获进阀温度时间序列的线性变化趋势, 然后利用 SVM 对进阀温度时间序列的非线性, 以提高预测的准确性. 在ARIMA模型预测的同时获得了残差数据, 将获得的残差部分作为SVM的输入, 根据SVM模型的输出进一步调整ARIMA的预测值, 使得预测值更加接近真实值.
实线为数据真实值, 虚线为模型在测试集上的预测. 从图6而言, ARIMA-SVM混合模型的进阀温度预测结果比ARIMA模型预测结果更加接近真实的阀冷进阀温度数据. ARIMA-SVM混合模型结合两个模型的优点. 首先使用 ARIMA 对电网时间序列进行预测, 捕获电网时间序列的线性变化趋势, 然后利用 SVM 对电网时间序列的非线性, 以提高预测的准确性. 在ARIMA模型预测的同时获得了残差数据, 将获得的残差部分作为SVM的输入, 根据SVM模型的输出进一步调整ARIMA的预测值, 使得预测值更加接近真实值.

|
图 6 混合模型预测 |
为了能够从整体评估各个模型的预测能力. 计算出各个模型的均方根误差、均方误差和平均绝对误差进行比较. 结果如表1所示, 根据本文选取的均方根误差、均方误差和平均绝对误差3个评价指标来衡量预测结果的准确性, 3个评价指标可以很好的衡量各个模型预测值和真实值之间的偏差和拟合精度, 值越小说明精度越高, 预测效果也越好. 从表1可以看出ARIMA-SVM混合模型在整体的误差上相比其他3个模型都有一定的优势, 能够更好的预测出进阀温度, 提高预测精度.
| 表 1 各模型的评价指标 |
7 结语
高压直流运行中换流阀会产生热能, 作为换流阀的关键设备和重要降温设备, 阀冷系统以水为介质将换流阀热能带出以达到冷却目的. 换流阀若要安全稳定地运行, 将设备运行时的温度维持在合理范围内至关重要. 进阀温度和出阀温度是阀冷系统最为关键的两个参数. 本文通过构建ARIMA模型、SVM模型、GRU神经网络模型以及ARIMA-SVM的混合模型对阀冷数据进行时序分析, 针对进阀温度这一关键参数进行预测. 实验结果表明, 虽然某些地方有些许偏差, ARIMA模型大体上能够较好地预测进阀温度但偏差比较大. SVM模型可以预测数据的变化趋势. GRU神经网络模型和ARIMA模型相比预测值更加接近进阀温度的真实值, 但在3个评价指标上稍劣于ARIMA-SVM混合模型. 通过在ARIMA模型分析线性数据的基础上结合SVM模型, 进而提高进阀温度预测准确性. 在ARIMA模型预测结果的基础上利用捕获的残差信息做进一步优化, 实验结果表明将传统时序模型与机器学习结合提出ARIMA-SVM的混合模型可以达到一个优化的结果.
| [1] |
徐德明, 徐健, 姚晓玲. 智能电网的关键技术与功能实现. 电工电气, 2011(11): 1-5, 41. DOI:10.3969/j.issn.1007-3175.2011.11.001 |
| [2] |
孙玉娇, 周勤勇, 申洪. 未来中国输电网发展模式的分析与展望. 电网技术, 2013, 37(7): 1929-1935. |
| [3] |
崔宗清, 孙仁龙, 邹荣盛. 换流站接地极在线监测系统电源的设计. 集成电路应用, 2019, 36(10): 46-48. |
| [4] |
张望平, 李家羊, 谌毅, 等. 高压直流阀冷却系统喷淋水净化工艺. 广东电力, 2018, 31(5): 107-114. |
| [5] |
罗永金, 杨垒, 马根坡, 等. 复合式换流阀冷却系统的设计与试验. 自动化仪表, 2018, 39(7): 11-15. |
| [6] |
崔鹏飞, 王海军, 国建宝. 直流输电工程阀冷系统在线仪表可靠控制策略. 广东化工, 2011, 38(12): 112-113. DOI:10.3969/j.issn.1007-1865.2011.12.057 |
| [7] |
原继东, 王志海. 时间序列的表示与分类算法综述. 计算机科学, 2015, 42(3): 1-7. DOI:10.11896/j.issn.1002-137X.2015.03.001 |
| [8] |
张美英, 何杰. 时间序列预测模型研究综述. 数学的实践与认识, 2011, 41(18): 189-195. |
| [9] |
吴志华, 韩燮, 张永梅, 等. 基于知识发现的时序数据分析方法. 测试技术学报, 2002, 16(S1): 571-575. |
| [10] |
杨海民, 潘志松, 白玮. 时间序列预测方法综述. 计算机科学, 2019, 46(1): 21-28. DOI:10.11896/j.issn.1002-137X.2019.01.004 |
| [11] |
王丽娜, 肖冬荣. 基于ARMA模型的经济非平稳时间序列的预测分析. 武汉理工大学学报(交通科学与工程版), 2004, 28(1): 133-136. |
| [12] |
何永沛. 时间序列数据挖掘在股市预测分析中的应用研究[硕士学位论文]. 重庆: 重庆大学, 2008.
|
| [13] |
Box GEP, Jenkins GM. Time Series Analysis: Forecasting and Control. San Francisco: Holden-Day, 1990.
|
| [14] |
Kim KJ. Financial time series forecasting using support vector machines. Neurocomputing, 2003, 55(1–2): 307-319. |
| [15] |
MacKay DJC. Bayesian interpolation. Neural Computation, 1992, 4(3): 415-447. |
| [16] |
MacKay DJC. Probable networks and plausible predictions–a review of practical Bayesian methods for supervised neural networks. Network: Computation in Neural Systems, 1995, 6(3): 469-505. |
| [17] |
Suykens JAK, Vandewalle J. Least squares support vector machine classifiers. Neural Processing Letters, 1999, 9(3): 293-300. |
| [18] |
Suykens JAK. Least squares support vector machines for classification and nonlinear modelling. Neural Network World, 2000, 10(1): 29-48. |
| [19] |
Das M, Ghosh SK. semBnet: A semantic Bayesian network for multivariate prediction of meteorological time series data. Pattern Recognition Letters, 2017, 93: 192-201. |
| [20] |
张敏. 跨语言文本情感分类技术研究[硕士学位论文]. 厦门: 华侨大学, 2017.
|
| [21] |
Anava O, Hazan E, Mannor S, et al. Online learning for time series prediction. Journal of Machine Learning Research, 2013, 30: 172-184. |
 2021, Vol. 30
2021, Vol. 30


