正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)是一种多载波调制技术. 因其具有高带宽效率、多径衰落鲁棒性的特点, 使得它在无线通信领域得以广泛地应用^[1]. 但目前OFDM系统仍具有一定缺陷, 其中最主要的缺陷就是其峰均比过高. 高的峰均比会增大OFDM系统对功率放大器(High Power Amplifier, HPA)的线性放大要求, 会使HPA工作效率以及ADC/DAC的量化噪声比受到一定影响.

针对OFDM系统高峰均比的问题, 专家学者们已经提出了一系列的解决方案, 包括限幅滤波(CF)、压扩变换(Companding)、部分传输序列(PTS)、选择性映射(SLM)、星座图扩展(ACE)等. 其中PTS与SLM属于加扰类技术, 它们因不会引起信号畸变且有良好的PAPR性能在工程中被广泛应用. 该类技术主要思想是首先对OFDM输入数据进行加扰后, 从中选出PAPR最小的一路信号进行传输, 从而降低高PAPR信号出现的概率^[2]. 但由于此类技术需要进行最佳相位因子的全遍历搜索, 所以使得整个系统有很高的计算复杂度, 这成为PTS技术应用于实际系统的巨大阻碍, 同时也成为本文研究的重点内容.

为了降低传统PTS技术的计算复杂度, 文献[3]提出一种迭代翻转算法IPTS, 在保证PAPR性能的同时, 大幅度降低了计算复杂度. 近些年来, 为了克服PTS技术的不足, 遗传算法^[4,5]、粒子群算法^[6-9]等智能算法也被广泛应用到PTS的最佳相位因子搜索中来, 本文主要针对PSO-PTS算法进行研究, 文献[10]提出DPSO-PTS算法, 该算法有效地降低计算复杂度且拥有较好的PAPR性能, 但DPSO-PTS算法有种群单一, 易陷入局部最优缺陷. 针对这一问题, 文献[11]中提出基于种群分类与动态学习因子的DPSO-PTS改进算法, 首先对粒子的适应度进行分类, 再依据适应度的好坏调整学习因子. 文献[12]提出用惯性权重线性递减策略达到全局搜索与局部搜索的平衡, 并用汉明距离对速度更新公式进行改进. 文献[13]用划分主子群与辅助子群的方式来增加种群多样性. 文献[14]提出一种基于动态离散粒子群优化的PTS相位系数搜索算法. 这些算法较DPSO-PTS算法相比, PAPR性能都有或多或少的改善.

本文针对DPSO-PTS的缺陷提出了新的解决方案, 首先定义一种新的惯性权重策略来平衡粒子的局部搜索和全局搜索的能力, 然后又通过引入对未知空间搜索的变异算子, 改进速度更新公式, 增大粒子寻优范围, 增强算法的种群多样性, 避免算法早熟而影响最优相位加权因子的搜索, 力求得到更优的PAPR抑制性能.

1 系统模型 1.1 OFDM系统模型及其PAPR的定义

假设OFDM系统包含N个子载波, 用 ${X_k} = \left\{ {{X_0},{X_1},} \right.$ $\left. {{X_2}, \cdot \cdot \cdot ,{X_{N - 1}}} \right\}$ 表示OFDM输入频域信号, 那OFDM时域信号序列 $x(n)$ 可以表示成:

${x_n} = \frac{1}{{\sqrt N }}\sum\limits_{k = 0}^{N - 1} {{X_K} \cdot {{\rm e}^{j2\pi kn/N}}} ,n = 0,1,2, \cdot \cdot \cdot ,N - 1$

(1)

那么OFDM信号PAPR定义为:

$r_{\rm {PAPR}}({x_n}) = 10\lg \frac{{\max \left\{ {|{x_n}{|^2}} \right\}}}{{E\left\{ {|{x_n}{|^2}} \right\}}}\;\;{\rm {}}$

(2)

其中, ${\max \left\{ {|{x_n}{|^2}} \right\}}$ 表示信号功率的最大值, ${E\left\{ {|{x_n}{|^2}} \right\}}$ 表示信号功率的平均值, PAPR的单位为dB.

一般情况下, 用互补累积分布函(Complementary Cumulative Distribution Function, CCDF)来描述PAPR的分布情况, CCDF表示的是峰均比大于某一门限值z的概率, 其数学表达式为:

$P(r_{\rm {PAPR}} > {\textit{z}}) = 1 - P\left( {r_{\rm {PAPR}} \le {\textit{z}}} \right) = 1 - {\left( {1 - {{\rm {e}}^{ - {{\textit{z}}^2}}}} \right)^N}$

(3)

1.2 部分传输序列(PTS)数学模型

图1为部分传输序列(PTS)技术实现框图. PTS技术的主要思想是将N个符号的输入数据块按一定的规则分割成V个大小相同、连续分布且互不相交的子块, 分割后的数据块可以表示成: $X = [{X^1},{X^2}, \cdots, {X^N}]$ , 然后让每个分割后的子块都乘以一个相应的相位因子 ${b^v} = {{\rm e}^{j\varphi v}}$ , $v = 1,2, \cdots, V$ , 随后将处理过的时域子块序列进行组合, 再经过IFFT变换可以得到候选序列 $x$ :

$x = {\rm {IFFT}}\left\{ {\sum\limits_{v = 1}^V {{b^v}{X^v}} } \right\} = \sum\limits_{v = 1}^V {{b^v}} \cdot {\rm {IFFT}}\left\{ {{X^v}} \right\} = \sum\limits_{v = 1}^V {{b^v}{x^v}} $

(4)

其中, $\left\{ {{x^v}} \right\}$ 为PTS. 选择使得PAPR最小的候选序列进行传输:

$\left[ {{{\tilde b}^1}, \cdots ,{{\tilde b}^V}} \right] = \mathop {\arg \min }\limits_{\left[ {{{\tilde b}^1}, \cdots ,{{\tilde b}^V}} \right]} \left( {\mathop {\max }\limits_{n = 0,1, \cdots ,N - 1} \left| {\sum\limits_{v = 1}^V {{b^v}{x^v}\left[ n \right]} } \right|} \right)$

(5)

这样, 最小PAPR向量的时域信号就可以表示成:

$\tilde x = \sum\limits_{v = 1}^V {{{\tilde b}^v}{x^v}} $

(6)

2 离散粒子群(DPSO)算法

粒子群算法是种群智能优化算法的一种, 它是通过模拟鸟群觅食过程中迁徙和群聚行为而提出的. 在PSO算法中, 粒子群中的每个粒子都有对应的位置、速度以及适应度, 每个粒子位置都代表所求问题的一个备选解, 其速度决定了粒子在搜索空间的飞行方向和距离, 而由具体优化目标函数确定的适应度决定着粒子的优劣程度.

粒子群算法首先随机初始化一群粒子, 然后迭代找到最优解. 在每次迭代中, 粒子都是通过跟踪两个极值来更新自己, 它们分别是粒子本身搜索到的个体最优解和整个种群的最优解. 若假设在D维的搜索空间里随机产生具有N个粒子的群体, 其中在第 $k$ 次迭代中, 第 $i$ 个粒子在第 $d$ 维的位置为 $x_{id}^k$ , 速度为 $v_{id}^k$ , 个体最优解为 $P_{id}^k$ , 全局最优解为 ${G^k}$ , 则粒子寻优遵循的速度和位置更新公式为:

$v_{id}^{k + 1} = wv_{id}^k + {c_1}{r_1}\left( {p_{id}^k - x_{id}^k} \right) + {c_2}{r_2}\left( {{G^k} - x_{id}^k} \right)$

(7)

$x_{id}^{k + 1} = x_{id}^k + v_{id}^k$

(8)

其中, $i = 1,2, \cdots ,N$ , $d = 1,2, \cdots ,D$ . $w$ 为惯性权重, ${c_1}$ 和 ${c_2}$ 被称为学习因子, 一般取 ${c_1} = {c_2} = 2$ , ${r_1}$ 和 ${r_2}$ 是(0,1)之间的伪随机数.

由于粒子群算法主要是针对连续问题提出的, 为了将粒子群算法用于求解离散空间极值问题, 有人在此基础上提出了一种二进制离散粒子群算法(Discrete Particle Swarm Optimization, DPSO). DPSO算法流程图如图2所示.

DPSO算法的粒子速度更新保持式(7)不变, 而粒子位置更新公式变为:

$x_{id}^{k + 1} = \left\{ {\begin{array}{*{20}{c}} 1,&{{\rm {random}} < {\rm {S{{ig}}moid}}\left( {v_{id}^{k + 1}} \right)} \\ 0,&{\rm {else}} \end{array}} \right.$

(9)

${\rm {Sigmoid}}\left( {v_{id}^{k + 1}} \right) = \frac{1}{{1 + \exp \left( { - v_{id}^{k + 1}} \right)}}$

(10)

其中, Sigmoid函数能将粒子的速度 $v_{id}^{k + 1}$ 取值控制在[0,1]之间, 而此时粒子速度 $v_{id}^{k + 1}$ 表示的是粒子的位置 $x_{id}^{k + 1}$ 取1的概率.

3 改进算法

虽然DPSO算法已具有良好的寻优性能, 但DPSO算法有易于早熟, 往往不能得到全局最优解缺陷. 对此本文在传统DPSO的基础上进行了改进, 首先由于惯性权重是决定DPSO算法搜索能力好坏的一个重要参数, 它可以调整算法全局搜索能力和局部搜索能力之间的平衡.

有人曾提出用基于线性递减策略的离散粒子群(LDPSO)算法来进行部分传输序列的最佳相位因子的搜索. 典型线性递减策略计算公式为:

$w_{\rm {lin}}^k = {w_{\max }} - \frac{{{w_{\max }} - {w_{\min }}}}{T}*k$

(11)

其中, $k$ 表示当前迭代次数, T为最大的迭代次数, ${w_{\max }}$ 为 $w$ 最大值, ${w_{\rm {m{{in}}}}}$ 为 $w$ 最小值. 此算法在搜索前期, $w$ 值较大, 侧重全局搜索能力, 有助于跳出局部极小值. 随着迭代次数增加, $w$ 不断减小, 算法局部搜索能力增强, 利于算法的收敛.

虽然LDPSO算法中 $w$ 的变化符合粒子的总体运行方向, 但算法也要考虑到粒子的实际运行情况. 因此, 这里提出基于进化速度-聚集度策略的动态离散粒子群(DDPSO)算法, DDPSO算法 $w$ 的变化是根据粒子进化速度和粒子的聚集程度实时进行调整的.

首先粒子进化速度会在一定程度上影响粒子搜索能力, 若粒子的进化速度较快, 应增大 $w$ 的值, 保持粒子的大范围搜索能力. 相反的若粒子进化速度较慢, 应减小 $w$ 的值, 增强粒子的局部搜索能力. 若设 $F\left( {{G^k}} \right)$ 为第 $k$ 次迭代的全局最佳解 ${G^k}$ 的适应度, 则粒子进化速度 ${k_v}$ 可以定义为:

${k_v} = \frac{{\min \left( {F\left( {{G^k}} \right),F\left( {{G^{k - 1}}} \right)} \right)}}{{\max \left( {F\left( {{G^k}} \right),F\left( {{G^{k - 1}}} \right)} \right)}}$

(12)

其次粒子聚集度反映了粒子的集中程度, 若粒子比较集中, 易陷入局部最优, 应增大 $w$ 的值, 若粒子比较分散, 应减小 $w$ 的值, 应适当减小粒子搜索空间. 这里设 ${\bar F^k}$ 为当前所有粒子适应度的平均值, 则粒子聚集度 ${k_a}$ 可以定义为:

${k_a} = \frac{{\min \left( {F\left( {{G^k}} \right),{{\bar F}^k}} \right)}}{{\max \left( {F\left( {{G^k}} \right),{{\bar F}^k}} \right)}}$

(13)

基于以上考虑, 基于动态变化惯性权重策略的离散粒子群算法 $w$ 的计算公式可表示为:

$w_{\rm {nolin}}^k = {w_{\rm {ini}}} - {k_v}{w_{{k_v}}} + {k_a}{w_{{k_a}}}$

(14)

其中, ${w_{\rm {ini}}}$ 为初始值, ${w_{{k_v}}}$ 和 ${w_{{k_a}}}$ 是用来调节进化速度 ${k_v}$ 和粒子聚集度 ${k_a}$ 的参数.

为了更好控制DPSO算法的整体搜索能力, 避免算法脱离实际运行和粒子低能或失效的问题. 本文结合LDPSO和DDPSO算法的优点, 并引入权重参数 ${\lambda _1}$ 和 ${\lambda _2}$ , 将两者进行结合来确定 $w$ 的值, 计算公式如下:

${w^k} = {\lambda _1}w_{\rm {lin}}^k + {\lambda _2}w_{\rm {nolin}}^k$

(15)

其中, ${\lambda _1},{\lambda _2} \in \left[ {0,1} \right]$ , 且 ${\lambda _1} + {\lambda _2} = 1$ , 通过调整 ${\lambda _1}$ 和 ${\lambda _2}$ 的值来控制LDPSO算法和DDPSO算法对惯性权重 $w$ 值的影响程度, 所以 ${\lambda _1}$ 和 ${\lambda _2}$ 的取值将直接影响到算法的收敛效率, ${\lambda _1}$ 的取值过大会使算法的惯性权重策略退化成线性惯性权重策略, 取值过小则退化成动态变化惯性权重策略.

为了增强种群的多样性, 避免出现早熟收敛现象, 本文又借鉴遗传算法变异的思想, 结合文献[15]将变异算法融入进来,使得粒子寻优范围得以扩大. 因此将式(7)速度更新公式替换成:

$v_{id}^{k + 1} = wv_{id}^k + {c_1}{r_1}\left( {p_{id}^k - x_{id}^k} \right) + {c_2}{r_2}\left( {{G^k} - x_{id}^k} \right) + \rho {r_3}\left( {R - x_{id}^k} \right)$

(16)

其中, R为解空间随机位置, $ {r}_{3}\in (0,1)$ 伪随机数, $\;\rho $ 为对未知世界的好奇系数, 一般设置 $\;\rho = 2$ .

传统PTS算法中对最优相位因子的搜索采取的是遍历搜索的方式, 其计算复杂度非常高, 这对实时性要求高的系统会产生偌大的影响. 而离散粒子群可避开遍历搜索, 可以有效地降低计算复杂度, 本文提出的改进算法还解决了传统离散粒子群算法易于早熟收敛, 往往不能收敛到全局最优的缺陷. 在本文提出的改进DPSO-PTS算法中, 相位因子集合{1, −1}分别映射为{1,0}, 粒子适应度函数为:

$f = \max \left( {\sum\limits_{v = 1}^V {{b^v}{x^v}} } \right)$

(17)

算法具体实现步骤为:

① 参数初始化. 设置粒子个数N、惯性权重w、学习因子 ${c_1},{c_2}$ 等参数; 随机初始化粒子群位置 $x_{id}^1$ , $i = $ $ 1,2, \cdots ,N$ , $d = 1,2, \cdots ,D$ 和速度 $v_{id}^1$ , $i = 1,2, \cdots ,N$ , $d = 1, $ $ 2, \cdots ,D$ ;

② 计算并比较每个粒子适应度f, 得到初始个体极值 $p_i^1$ 和全局极值 ${G^1}$ ;

③ 根据式(15)计算w, 根据式(16)和式(9)分别更新粒子速度和位置;

④ 更新个体极值和全局极值;

⑤ 若当前迭代次数小于预设迭代次数T, 重复③和④, 否则退出循环并执行⑥;

⑥ 将迭代得到的全局极值作为PTS算法的相位因子, 通过式(6)得到具有最小PAPR的OFDM信号进行传输, 算法结束.

4 仿真结果

为了验证本文算法用于降低PAPR的有效性, 本节进行了相应的仿真实验. 仿真参数如下: 采用 16-QAM调制, 子载波数 $N = 256$ , 过采样因子 $L = 4$ , 随机-交织分割, 相位因子 $W = \left\{ {1, - 1} \right\}$ , 粒子个数 $P = 10$ , 一般取学习因子 ${c_1} = {c_2} = 2.0$ . 在线性递减惯性权重策略中, 为了使实验结果更具说服力, 取 ${w_{\max }} = 1.2$ , ${w_{\min }} = 0.2$ , 与MDPSO-PTS算法初始化参数保持一致. 而对于动态惯性权重策略而言, 根据文献[16]仿真结果显示, 取 ${w_{\rm {ini}}} = 1.0$ , ${w_{{k_v}}} \in (0.4,0.6)$ , ${w_{{k_a}}} \in (0.05,0.2)$ , 算法性能最优, 因此这里令 ${w_{{k_v}}} = 0.5$ , ${w_{{k_a}}} = 0.2$ . 本文算法以线性惯性权重策略为主, 动态变换惯性策略为辅, 文中取 ${\lambda _1} = 0.6$ .

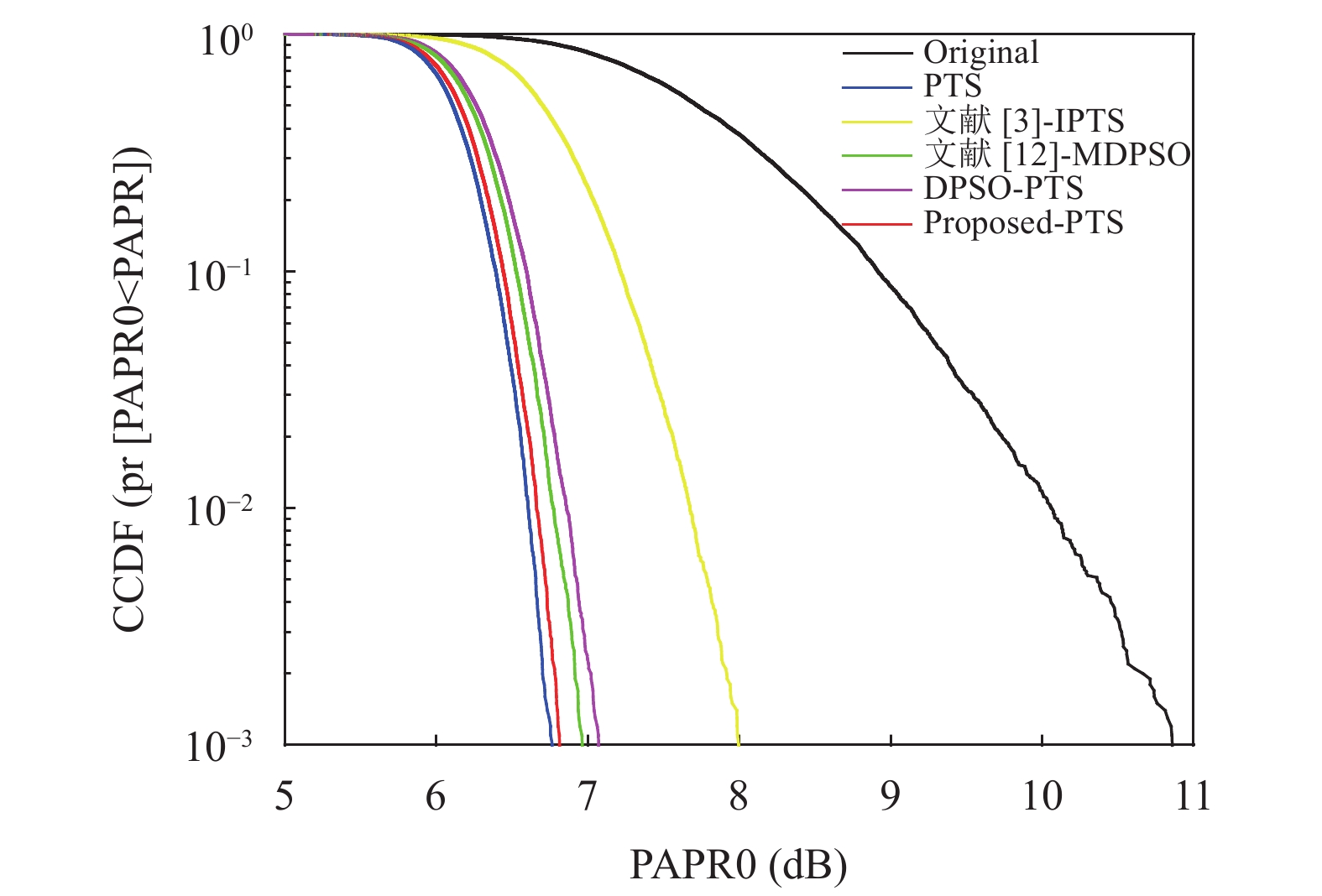
图3为本文算法与其他几种不同算法的CCDF性能曲线对比图. 当 $CCDF = {10^{ - 3}}$ 且迭代次数为20时, 原始信号的PAPR值为10.82 dB, 次优IPTS算法的PAPR值为8.05 dB, DPSO-PTS算法的PAPR值为7.06 dB, 文献[12]提出的MDPSO-PTS算法的PAPR值为6.96 dB, 本文所提算法的PAPR值为6.8 dB, 传统PTS算法的PAPR值6.77 dB, 本文所提算法较原始信号、次优IPTS、DPSO-PTS、文献[12]的MDPSO-PTS相比, 分别优化了4.02 dB、1.25 dB、0.26 dB、0.16 dB, 较传统PTS算法相比差了0.03 dB, 但传统PTS算法计算复杂度比本文算法计算复杂度要高出许多.

图4为本文算法、传统PTS算法以及DPSO-PTS算法在不同迭代次数下的CCDF性能曲线. 从仿真结果可以看出, 本文所提算法能很好地改善系统的PAPR. 在 $CCDF = {10^{ - 3}}$ 处, 在相同的迭代次数下, 本文算法PAPR性能优于DPSO-PTS算法, 稍差于传统PTS算法.

由表1具体数据可以看出本文算法PAPR性能随着迭代次数的增加而有所提升, 在迭代次数为5、10、20、30时, 本文算法较DPSO-PTS算法相比, 分别优化了0 dB、0.1 dB、0.26 dB、0.28 dB. 同时也可以看出DPSO-PTS算法经过10次迭代后就收敛了, 而本文算法在30次迭代时才基本收敛, 说明本文算法在一定程度上有效解决了DPSO-PTS算法易陷于局部最优解的问题. 但在实际系统中, 建议算法迭代次数为20次最佳, 牺牲极小部分的PAPR性能, 可以避免多余的计算量.

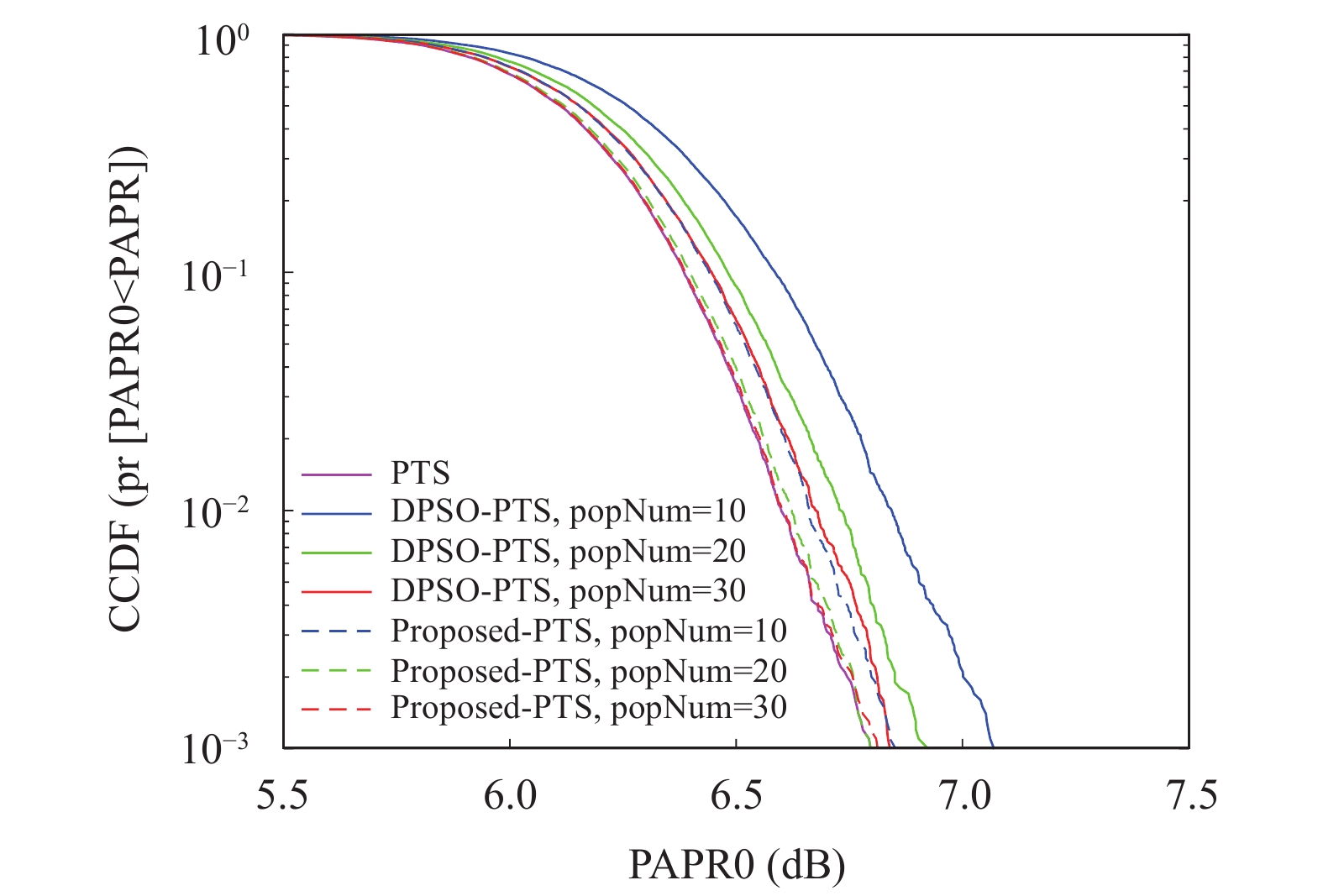
图5为本文算法、传统PTS算法以及DPSO-PTS算法在不同粒子数下的CCDF性能曲线. 从仿真结果可以看出算法的PAPR抑制性能会受到粒子数的影响. 在 $CCDF = {10^{ - 3}}$ 处, 当迭代次数为20且粒子数popNum=[10, 20, 30]时, 本文算法较DPSO-PTS算法相比, 分别优化了0.23 dB、0.12 dB、0.05 dB. 也可以看出本文算法随着粒子数的增加PAPR性能改善不太明显, 而粒子数会增加复杂度, 因此算法粒子数为10最为合适.

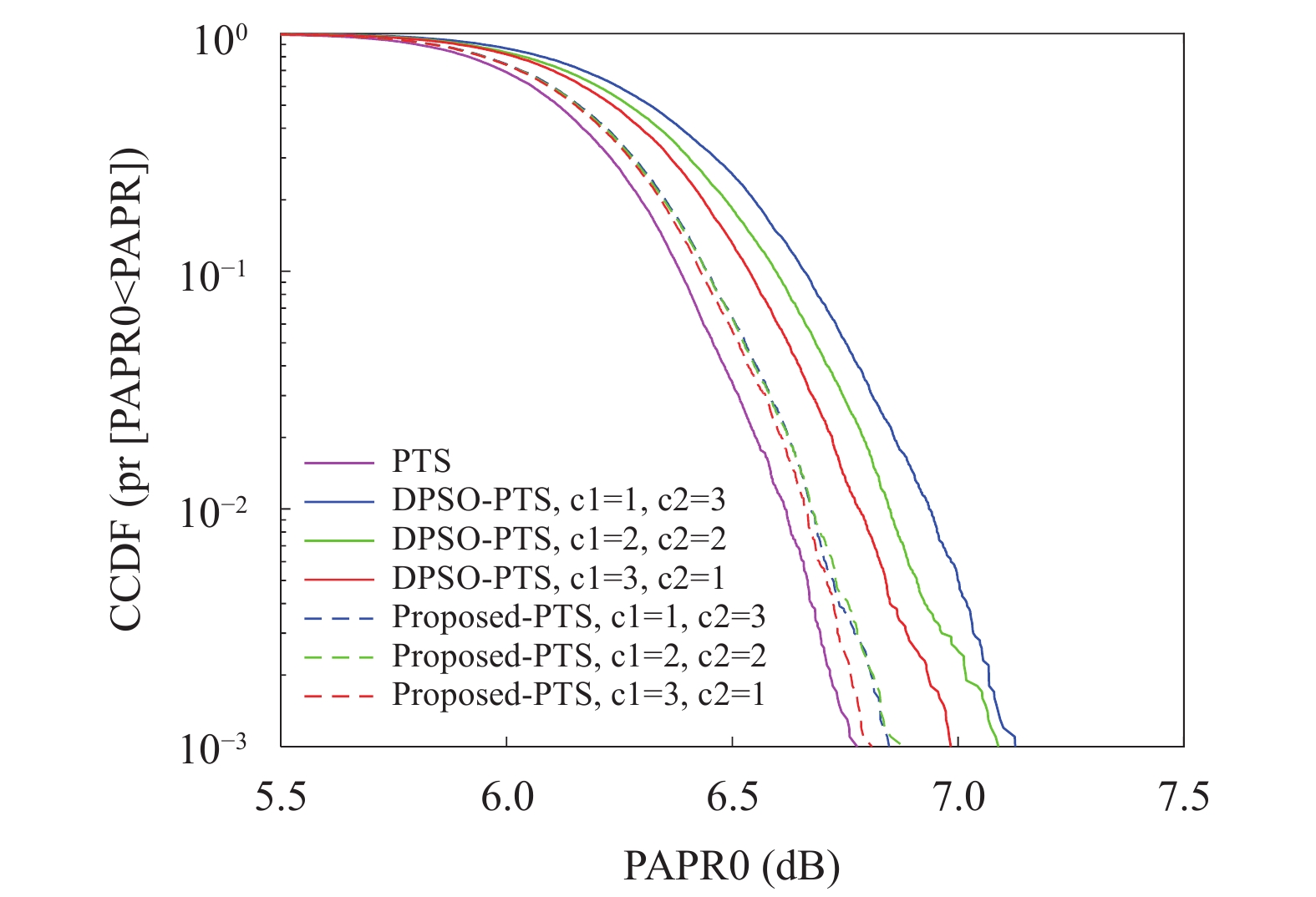
图6为本文算法、传统PTS算法以及DPSO-PTS算法在不同学习因子下的CCDF性能曲线对比图. 由图可看出, 在不同学习因子下, 本文算法的PAPR抑制性能都优于DPSO-PTS算法, DPSO-PTS算法受学习因子的影响较大, 本文算法受其影响较小, 考虑是惯性权重和学习因子双重作用的缘故.

图7为本文算法在不同权重参数下的CCDF性能曲线. 由图中可以看出, 本文算法在 ${\lambda _1} = 0.6$ 情况下表现出更加优秀的PAPR抑制性能, 也解释了本文算法以线性递减惯性权重策略为主, 以动态惯性权重策略为辅的原因.

图8为本文算法在不同分割方式下的CCDF性能曲线. 由仿真结果可以看出随机分割的PAPR性能最佳, 但随机分割的计算复杂度很高, 随机-交织分割方式与随机分割方式相比, PAPR性能虽差了0.1 dB, 但是计算复杂度要低很多, 所以本文前面采用的随机-交织分割方式进行仿真.

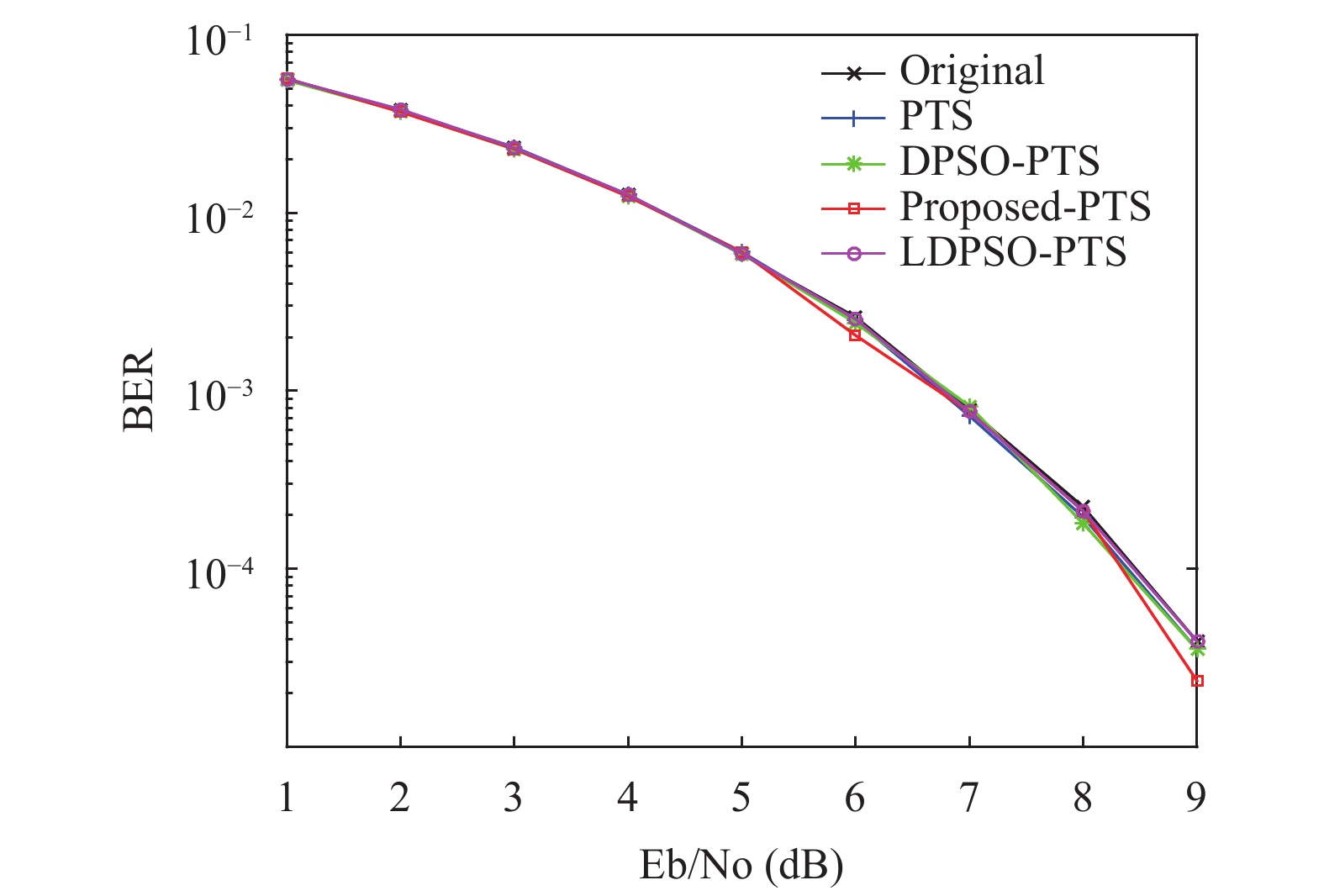
图9为所提算法与其他几种算法的误码率性能比较图. 由图可知, 本文所提算法与原始信号、传统PTS、传统DPSO-PTS这几种算法相比, 误码率性能几乎相同, 说明本文算法不会产生多余的信号失真.

5 结论与展望

针对传统 PTS 算法计算复杂度高的问题, 本文提出一种基于新的惯性权重策略和变异算子的改进DPSO算法, 此算法w值的确定同时考虑了粒子的总体运行方向和粒子的实际运行情况, 在此基础上还引入变异算子增强算法种群多样性. 其可以快速且准确地找出最优的相位因子, 得到具有较小的PAPR的OFDM信号. 仿真结果表明, 在误码率基本不变的情况下, 本文算法与IPTS、传统DPSO-PTS等算法相比, 拥有更好的PAPR性能, 与传统 PTS算法相比, PAPR性能略微下降,但其计算复杂度会有明显改善, 且相位因子集合W和分块数V越大改善效果会更加明显.