学习者特征指对学习者从事学习产生影响的心理、生理和社会的特点, 包括认知的、情感的和社会的特征; 其中, 属于认知方面的特征被称作学习者认知特征, 它作用于学习的信息加工过程[1]. 当代教育心理学认为学习者的认知能力水平是学习者的认知特征的重要组成部分, 认知语言学认为词汇学习就是一种信息加工过程, 可见, 学习者的认知特征(认知能力和认知风格)会影响词汇学习的过程.
近年来, 多媒体学习的相关研究进一步表明学习者的认知能力水平是影响第二语言词汇学习绩效的一个主要因素. 在多媒体材料呈现方式对ESL (English as a Second Language)词汇学习绩效的效应研究中, Chun以非英语专业大学生为被试群体, 研究结果表明, “文字+图片”比“文字+视频”更有效[2], 而Alseghayer以英语专业大学生为被试群体, 他的研究却得出相反的结论[3], Toylor 的研究结论是将词汇学习绩效的差异归因于学习者的认知能力水平的不同[4].
学习者认知风格对多媒体英语词汇学习绩效的主效应同样显著. Riding等将认知风格定义为: 个体在认知过程中所表现出来的习惯化的行为模式[5]. 可见, 学习者认知风格的差异不但会导致出现选择不同学习内容的行为, 而且会影响学习者在多媒体词汇学习时的学习绩效. Reid指出, 个体学习者的认知风格决定了他们选择何种学习策略, 从而影响他们的词汇学习绩效[6]. Oxford对语言学习成绩的各项研究也揭示出学习者认知风格倾向的重要性[7]. 至此可以得出, 学习者认知特征和学习内容确实存在适应性关系. 设计一种能测量出这种适应性关系、随后为学习者推送相合适的学习内容的工具就显得尤为必要.
国内外近年来有一些关于自适应学习模型构建的研究. 如在国内, 陈品德较早地利用Web平台制作适应性学习系统[8]; 菅保霞等深入大数据背景, 建立基于元分析视角的自适应学习个性特征模型[9]. 而在国外, 大量的自适应学习平台已应用在实践当中, 自适应技术逐渐变成一套为学习者提供更广泛的个性化学习服务的教育技术工具. 哥伦比亚大学开发的Alchemy学习平台, 意图为学生应对即时和具体的大规模在线学习的挑战; 目前它仍处于beta版, 但Alchemy有能力适应不同的班级规模, 并支持灵活的学习, 以及潜在的个性化的大规模在线学习体验[10]. 佛罗里达大学则重新设计了具有适应性学习的初级西班牙语课程, 以回答学生在这些课程中遇到的无数问题; 收集到的初步数据表明, 学生掌握程度明显提高了, 学生对教学调查的看法愈发积极[10]. Alchemy平台尚处于试用阶段, 而佛罗里达大学的适应性课程没有英语课程, 分析当前研究现状可知, 有关英语学习的适应性学习软件的研发仍需完善. 此外, 已有的自适应学习模型、系统和平台, 鲜有把机器学习的概念、方法运用到多媒体学习认知领域的实践当中. 针对以上不足, 本研究试图通过改进、优化AdaBoost算法, 并将该算法与基于IRT (项目反应理论)的计算机自适应测验相整合, 以此构建一个融入了机器学习算法的新型英语词汇自适应学习模型. 该项研究具有一定的理论价值和现实价值.
1 模型的理论依据 1.1 自适应学习技术自适应学习技术是指根据学习者独特的个性特征, 通过呈现适当的信息、教学材料, 反馈和建议来提供一个符合学习者需要的智能调整环境[11]. 自适应学习系统通过将学习者的个体差异和学习情境纳入其中, 从而提高学习效果, 需要付出较少的努力, 减少所需的时间, 并产生更高的学习者满意度. 本模型是一个典型的自适应学习模型, 它遵循自适应学习系统两个必要步骤: 第一步涉及学习者静态建模和动态建模, 静态建模是一种学生模型或情境模型只设置一次的方法, 指学习者第一次访问系统时(系统初始化); 相反, 动态建模方法会持续监控学习者及其所处的情境, 并经常更新“学生/情境”模型的信息(系统参数更新). 第二步, 确定学习者特征及其当前情况(学习者某个认知特征, 学习者对某种学习内容的自我选择情况), 可以用来给学习者提供个性化的学习体验(自适应学习内容呈现). 因而, 本模型的参数信息(条件概率)被用来提供自适应性, 为学习者供应自适应性功效的适应性学习引擎(系统)是模型的最终产品.
1.2 机器学习、条件概率、AdaBoost算法机器学习是当前人工智能领域最受欢迎的课题, 取得了丰硕成果. 本模型也是将机器学习的概念、方法借鉴到多媒体学习认知研究领域的一次尝试. 机器学习的核心是参数, 训练是学习训练集数据的过程, 也是寻找最优参数的过程, 依照已被严格推导出的数学算法, 来达到参数优化的目的[12]. 给予本模型的启发是引入训练的思想, 可以让模型自动地调整参数(条件概率)以拟合真实的适应性关系, 使其成为动态建模学习工具.
具有不同认知特征的学习者对学习内容的适应性程度称为适应度, 即适应度用于表示具有某个认知特征的学习者对某种学习内容的适应性程度, 用条件概率P(Aj|Bi)表示[13], 意为在事件Bi发生的条件下, 事件Aj可能发生的概率; Bi表示学习者具有第i类认知特征, Aj表示学习者对第j种学习内容的选择.
AdaBoost算法全称为Adative Boost, 即自适应的增强算法, 旨在将多个“弱学习器”通过适应地调整概率, 组合成为一个“强学习器” [14]. 站在本模型的角度, AdaBoost算法如下: 输入训练数据集T={(x1, y1), (x2, y2), …, (xN, yN))}, 其中xi∈Rn, yi∈y={−1, +1}; 弱学习器. 输出: 最终强学习器G(x).
(1)初始化弱学习器的概率P1
| $ {P_1} = ({p_{11}}, \cdots ,{p_{1i}}, \cdots ,{p_{1N}}),{p_{1i}} = \dfrac{{\rm{1}}}{N},i = 1,2, \cdots ,N $ | (1) |
(2)对迭代次数m. 有m=1, 2, ···, M
(a)使用训练数据集学习, 得到弱学习器的线性组合Gm(x)
| $ {G_m}\left( x \right):x \to \left\{ { - 1, + 1} \right\} $ | (2) |
(b)计算Gm(x)在训练数据集上的误差率em
| $ {e_m} = \sum\limits_{i = 1}^N {p_{mi}I(G_m(x_i) \ne y_i)} $ | (3) |
(c)计算Gm(x)的系数am
| $ {a_m} = \frac {1}{2}\log \frac{{{\rm{1 - }}e_m}}{{e_m}} $ | (4) |
(d)更新弱学习器的概率Pm+1
| $ {P_{m + 1}} = \left( {{p_{m + 1}},1, \cdots ,{p_{m + 1}},I, \cdots ,{p_{m + 1}},N} \right) $ | (5) |
| $ \begin{array}{l} {p_{m + 1,i}} = \dfrac{{{p_{mi}}}}{{{Z_m}}} \exp ( - {a_m}{y_i}{G_m}({x_i})),i = 1,2, \cdots ,N \end{array} $ | (6) |
| $ {Z_m} = \sum\limits_{i = 1}^N {{p_{mi}}\exp ( - {a_m}{y_i}{G_m}({x_i}))} $ | (7) |
这里Zm是规范化因子, 它使Pm+1成为一个概率
(3)构建弱学习器的线性组合, 得到最终强学习器G(x)
| $ G\left( x \right) = \sin \left( {\frac{M}{{m = 1}}{a_m}{G_m}(x)} \right) $ | (8) |
AdaBoost算法步骤是: 先假设每个弱学习器作用相同,也就是说弱学习器有着均匀的概率, 然后反复学习, 作出m=1, 2, ···, M次迭代, 每次迭代步骤为: 使用当前弱学习器概率、计算误差率、计算弱学习器系数、更新弱学习器概率、线性组合弱学习器. 由此看出, AdaBoost算法所解决的问题, 尤其是适应地更新概率, 与模型面临的最中心问题—根据学习者对每个单词的学习内容的选择情况, 适应度如何自动地变化, 两者基本一致, 这正是模型公式参考AdaBoost算法公式的理由. 针对问题, 模型也对AdaBoost算法进行了简化和改进: (1)对于每个单词, 模型只有一次训练, 也只需要一次适应度更新, 同一单词不需要多次迭代, 因而置m=1; (2)学习者对每个单词只能选取一种学习内容, 对第i种学习内容xi, 若被选择则yi=+1,否则yi=−1,根据AdaBoost算法的阙值化器计算得em=1/N,
基于IRT项目反应理论的自适应测验常利用计算机实施, 又称为计算机自适应测验(Computerized Adaptive Testing, CAT), 作为一种新式的测验方式广泛应用于教育测量与评价中. 基于项目反应理论的自适应测验是这样进行的: 从测试项目的应答结果对被测试者的能力水平进行估计(或估计值的修正). 按照估计的能力水平, 从项目数据库中检索出与之匹配、适宜的测试项目[15].
为得到稳定的适应度, 模型的求解过程参照了基于项目反应理论的自适应测验, 既有相似, 又有区别. 相似之处是, 都可以根据用户的反应模式进行参数更新, 且参数的更新时机都在学习者每完成一个项目的学习后立刻重新计算, 操作流程类似. 区别之处有两点: (1)模型所使用的运算公式是AdaBoost算法的公式; (2)模型的结束判定使用最近3次每个适应度的标准差(均小于某个精度值).
2 模型的构建本模型属于动态模型, 其构建主要分为两个步骤: (1)建立问题的数学模型: 模型的数学公式, 是承待解决问题的抽象描绘; (2)数学模型求解: 模型的算法, 是解决问题的具体流程. 第(1)步包括模型的问题描述与公式, 第(2)步包括模型的算法流程设计和算法伪代码实现, 之后加入模型的讨论.
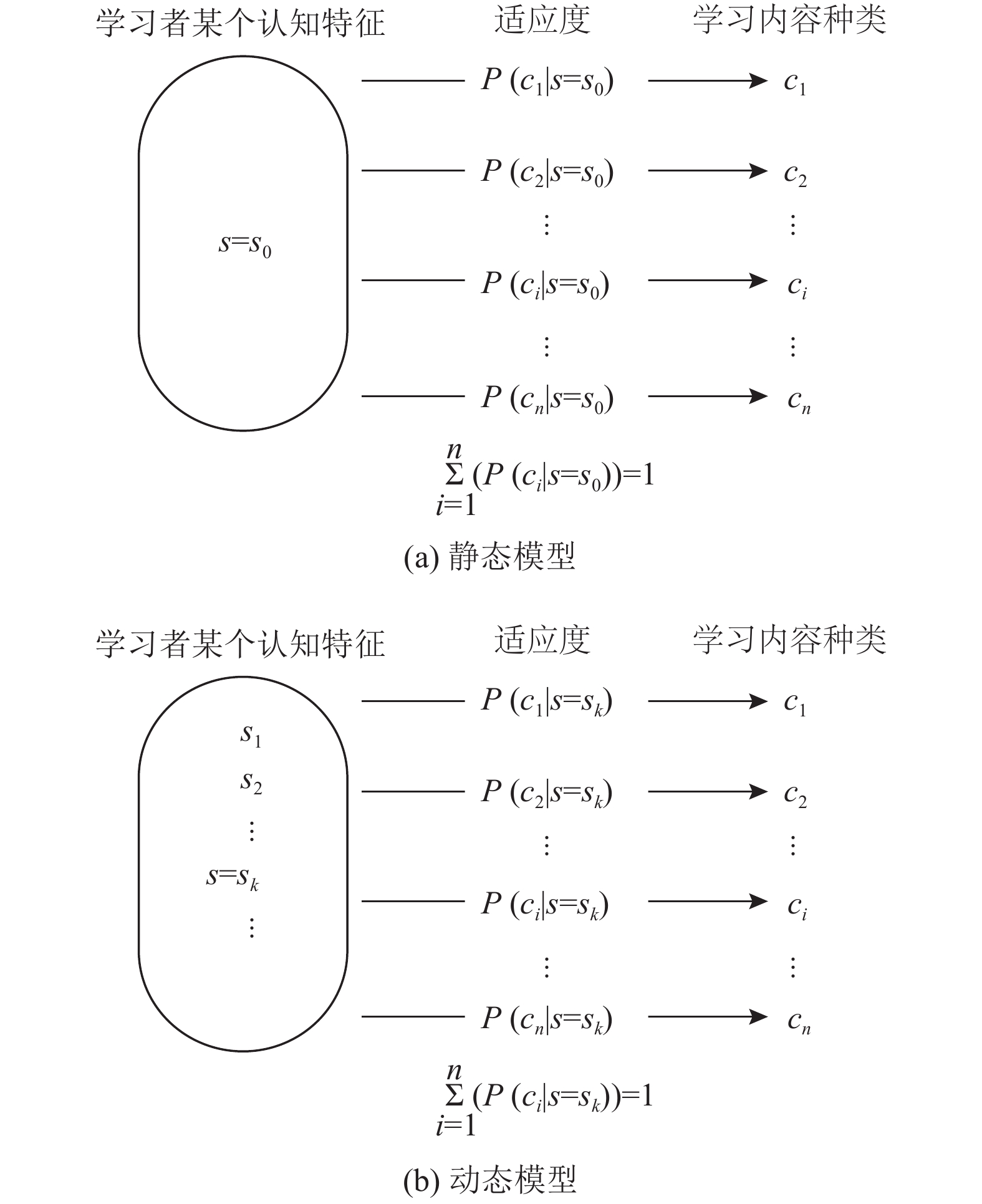
2.1 模型的问题模型要解决的问题是, 测得学习者某个认知特征对某种学习内容的适应性关系, 根据该认知特征在学习过程中是否会发生改变, 应分为两种情况: (1)该认知特征在学习过程中几乎不会改变(如认知风格), 此时模型是静态模型, 如图1(a)所示. 适应度P(ci|s=s0)(其中i=1, 2, ···, n)表示, 在学习者某个认知特征取值为s=s0的条件下(s0是一个常量值), 学习者对第i种学习内容选择的概率; (2)认知特征在学习过程中很可能会改变(如认知能力), 此时模型是动态模型, 如图1(b)所示. 适应度P(ci|s=sk) (其中i=1, 2, ···, n)表示, 在学习者某个认知特征取值为s=sk的条件下(sk是一个变量值), 学习者对第i种学习内容选择的概率. 无论何种情况, 每种学习内容都对应着1个适应度, 适应度会随着训练次数增加而不断更新, 且所有适应度总和恒为1. 总的来说, 模型被视为一个动态模型.
|
图 1 学习者某个认知特征对某种学习内容的适应性关系图 |
2.2 模型的公式
模型旨在解决学习者在学习一个单词后, 适应度的动态更新. 模型的公式参考了AdaBoost算法公式, 并对其简化. 公式具体表述如下:
输入: 将学习者对一个单词的选择情况数据集, 作为一次训练的训练数据集, 记
将第2.1节中
输出: 更新后的适应度
(1)计算误差率e
| $ e = \frac{{\rm{1}}}{n} $ | (9) |
(2)计算系数alpha
| $ alpha = \frac {1}{2}\log \frac{{{\rm{1 - }}e}}{e} $ | (10) |
(3)得到更新后的
| $ {P_i} = {\rm{ }}{P_i}*\exp ( - alpha*{y_i}*( - 1)) $ | (11) |
| $ Z = \sum\limits_{i = 1}^n {Pi} $ | (12) |
| $ {{{\hat P}_i} = \frac{{{P_i}}}{Z}} $ | (13) |
(4)得到更新后的适应度
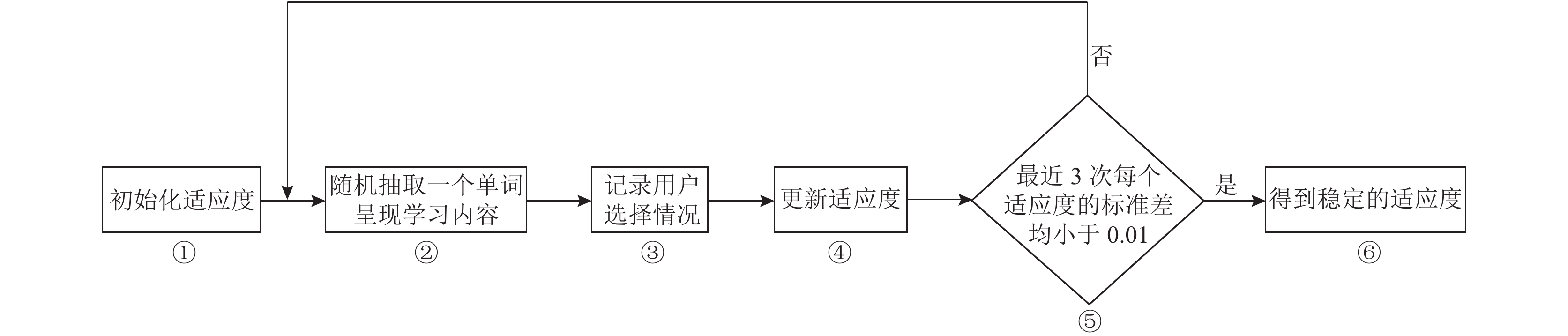
模型的算法流程参照了基于项目反应理论的自适应测验流程, 如图2所示, 对图中每个步骤进一步解释如下.
|
图 2 模型的算法流程设计图 |
(1)模型初始化(开始)
① 假定每种学习内容被选择的概率相同, 使用均值初始化适应度.
(2)模型一次训练(继续)
② 从词库内随机抽取一个未学习过的单词, 呈现不同种类的学习内容.
③ 记录用户选择了何种学习内容.
④ 重新计算每个适应度.
(3)模型结束判定(结束)
⑤ 判断每个适应度, 最近3次训练的标准差是否小于0.01, 若不满足回到第②步, 否则进入第⑥步.
⑥ 每个适应度的波动范围均较小, 得到稳定的适应度.
2.4 模型的算法伪代码实现模型的中心任务是适应度更新的实现, 下面以第i种学习内容为例, Python伪代码编程如算法1.
算法1. 求第i种学习内容更新后的适应度
输入:
输出:
1. If initflag: #如果是初始化
2. Pi=1/n #适应度为平均值, n为学习内容的种类数
3. Else:
4. Pi=ReadDB(i) #从数据库里读取上一次计算得到的第i种学习内容对应的适应度
5. e = 1/n #误差率
6. alpha = 0.5*Log((1−e)/e) #系数
7. Pi = Pi * Exp(−alpha*Yi*(−1)) #Pi更新开始, 若第i种学习内容被学习者选择, 则Yi = 1, 否则Yi = −1
8. z = Sum(Pi) #规范化因子
9. Pi = Pi/z # Pi更新完成
10. If Std(Pi, LastPi, LastLastPi) < 0.01 #如果最近3次适应度的标准差小于0.01
11. If OthersStd() < 0.01 #如果最近3次每个适应度的标准差均小于0.01
12. Finish() #系统结束运行
13. Else:
14. Continue() #系统继续运行
15. Else:
16. Continue() #系统继续运行
2.5 模型的讨论需要讨论的是, 模型中学习内容种类n数值的确定. 以研究材料呈现方式对英语词汇学习绩效的影响为例, 应先用文献法、专家评价法筛选词汇材料的有意义组合呈现方式. 所谓有意义组合呈现方式, 是指词汇呈现材料的组合是不违背多媒体学习认知理论的基本原理的, 符合人们外语词汇学习习惯, 或者已经证明这样的组合对词汇学习有促进作用[16]. 已有研究表明, 有意义组合呈现方式大概有8至12种, 所以当模型被实际运用到该项研究时, n数值取值范围尽量为8至12.
2.6 模型的验证为进一步佐证模型的有效性, 提升其现实应用价值, 遂根据模型开发出原型系统, 并实施试测. 原型系统由服务端和客户端两部分组成, 服务端负责使用模型的算法, 以更新被试的适应度; 客户端负责呈现不同种类的学习内容, 供被试选择. 服务端是一个基于Flask框架编写的Web程序, 实验环境为Windows 10+Python3.7.2+Flask 1.1.1, 服务端数据库使用flask_sqlalchemy; 客户端是一个移动APP, 实验环境为Windows 10+Android Studio 3.3.2+Android SDK 28+安卓模拟器; 客户端APP运行在安卓模拟器, 服务端Web程序运行于本地计算机, 安卓模拟器与本地计算机通过WLAN无线网卡桥接, 用于建立客户端和服务端的网络连接. 客户端request数据提交方式为Post, 服务端处理由客户端发来的request数据.
实验中, 学习内容种类有5种, 分别为词形变化、词根词缀、图片、短语、例句; 被试选取自大一非英语专业的女生; 测试词汇库里的词汇, 均借助《牛津词典》选用那些被试不认识, 且难度相近的单词. 系统初始化时, 设置参数n (学习内容种类)数值为5, 参数e (误差率)数值为0.2. 以其中一名被试的实验结果为例, 如图3所示, 系统在训练时, 处于快速收敛的状态, 数值变化也比较合理, 经过9次训练后, 计算出稳定的适应度, 即(0.000243, 0.994658, 0.003885, 0.000243,0.000971). 可以看出, 该名被试更加适合词根词缀型学习内容, 这与早前的问卷调查结果相一致.
实验结果表明, 该系统符合自适应学习系统的要求, 其自适应性体现于: 根据被试反应, 不断更新被试适应度参数, 最终对被试适应度作出估计; 同时, 伴随着测验过程的发生, 系统会为被试呈现出, 当前适应度最大的、所对应的某种学习内容, 即系统适应了该名被试. 这一点, 相似于基于IRT(项目反应理论)的计算机自适应测验中的能力参数估计的情况.
再者, 以往类似研究所使用的测量工具大多局限于量表(如学习风格量表), 它们的量化能力明显有限, 很难测得同一变量的每个水平之间的准确差异值, 而用本模型作为替代性测量工具, 可提高相关评估实证研究的量化水平.

|
图 3 某名被试的系统试测结果 |
3 总结
综上所述, 研发了一个基于适应度的英语词汇自适应学习模型, 将该模型现实构建, 就获取了一个适应性学习引擎(系统), 它能够侦测学习者某个认知特征对某种学习内容的适应性关系, 并调整学习内容的推送, 最终使得学习内容与特定学习者相匹配. 本模型希望应用于英语词汇学习的相关研究, 但也能方便地迁移到其他学习研究上, 具有良好的可靠性和鲁棒性. 此模型的不足之处在于两点, 一是模型尚未侦测学习者某个认知特征的具体取值, 而将此看作预设. 二是尚未引入学习绩效, 学习者根据自我喜好而选择的学习内容, 无法肯定使用这些学习内容就可以获得高的学习绩效, 同时也不能通过学习绩效分析出学习损失. 以上功能是进一步增强适应性学习引擎(系统)对学习者的自适应性能力的要点所在. 这也是要展开的后续工作.
| [1] |
陈琦, 刘儒德. 教育心理学. 2版. 北京: 高等教育出版社, 2011: 29–46.
|
| [2] |
Chun DM, Plass JL. Effects of multimedia annotations on vocabulary acquisition. The Modern Language Journal, 1996, 80(2): 183-198. DOI:10.1111/j.1540-4781.1996.tb01159.x |
| [3] |
Al-seghayer K. The effect of multimedia annotation modes on l2 vocabulary acquisition: A comparative study. Language Learning & Technology, 2001, 5(1): 202-232. |
| [4] |
Taylor A. The effects of CALL versus traditional L1 glosses on L2 reading comprehension. Calico Journal, 2006, 23(2): 309-318. |
| [5] |
Riding R, Cheema I. Cognitive Styles—an overview and integration. Educational Psychology, 1991, 11(3–4): 193-215. |
| [6] |
Reid JM. The learning style preferences of ESL students. Tesol Quarterly, 1987, 21(1): 87-111. DOI:10.2307/3586356 |
| [7] |
Oxford RL. Language learning styles and strategies: Concepts and relationships. International Review of Applied Linguistics in Language Teaching, 2003, 41(4): 1613-4141. |
| [8] |
陈品德. 基于Web的适应性学习支持系统研究[博士学位论文]. 广州: 华南师范大学, 2003: 1–132.
|
| [9] |
菅保霞, 姜强, 赵蔚, 等. 大数据背景下自适应学习个性特征模型研究−基于元分析视角. 远程教育杂志, 2017, 35(4): 87-96. |
| [10] |
Brown M, McCormack M, Reeves J, et al. 2020 educause horizon reportTM teaching and learning edition. Louisville, CO: EDUCAUSE, 2020.
|
| [11] |
MichaelSpector J, DavidMerrill M, Elen J, 等. 教育传播与技术研究手册(下册). 任友群, 焦建利, 刘美凤, 等, 译. 4版. 上海: 华东师范大学出版社, 2015: 966–977.
|
| [12] |
斋藤康毅. 深度学习入门: 基于Python的理论与实现. 陆宇杰, 译. 北京: 人民邮电出版社, 2018: 82.
|
| [13] |
Tan PN, Steinbach M, Kumar V. 数据挖掘导论. 范明, 范宏建, 等, 译. 2版. 北京: 人民邮电出版社, 2011: 141.
|
| [14] |
李航. 统计学习方法. 2版. 北京: 清华大学出版社, 2019: 157–159.
|
| [15] |
傅德荣, 章慧敏. 教育信息处理. 北京: 北京师范大学出版社, 2001: 120–133.
|
| [16] |
李怀龙, 张家年, 高玉兰. 中国学习者英语词汇刻意学习的研究设计——多媒体学习理论视角. 现代教育技术, 2014, 24(8): 62-69. DOI:10.3969/j.issn.1009-8097.2014.08.009 |
 2021, Vol. 30
2021, Vol. 30



