1 引 言

随着移动互联网的发展, 数据规模也以前所未有的速度不断增长, 数据属性之间的相互关系变得复杂多样, 高维数据已是一种常见的数据发布类型. 随着数据挖掘和分析技术的发展, 高维数据的发布具有更高的信息价值, 但高维数据中通常包含大量隐私信息, 如果使用不当将造成隐私泄露^{[1, 2]}. 为了保证高维数据发布过程中不会泄露隐私信息, 在发布之前使用差分隐私^{[3, 4]}保护技术进行处理. 如果直接对高维数据进行差分隐私处理, 存在添加噪音过多, 数据可用性差等问题. 其中差分隐私预算的分配方式直接影响数据的可用性与安全性关系, 而不同数据机构对于发布数据集安全性和可用性之间的关系需求各不相同, 数据保护级别更高的数据机构更注重数据的安全性; 而主要提供数据进行应用的数据机构则更倾向于数据的可用性.

目前已有的面向高维数据发布的差分隐私算法有概率图模型^[5-7]、阈值过滤技术^[8]以及投影技术^[9], 这些技术通过维度转换达到降维效果, 减少噪音添加对数据可用性的影响. 降维效果的好坏直接影响数据的可用性, 而阈值过滤技术和投影技术忽略了高维属性之间普遍存在依赖关系, 采用直接截断的降维方法, 大大降低了数据的可用性. 文献[5-7]利用指数机制^{[3, 10]}挑选属性关系对, 受候选空间大小和隐私预算分配方式的影响, 空间越大挑选的属性关系对越不准确. 同时, 单一的隐私预算分配方式为敏感性不同的属性数据分配相同的隐私预算, 导致隐私预算无法根据数据可用性与安全性的个性化需求合理分配, 存在隐私浪费的问题.

基于在高维数据发布过程中, 数据安全性与可用性受降维算法效果和隐私预算分配方式的影响, 为满足发布数据集安全性与可用性的个性化需求, 本文提出个性化隐私预算分配(Personnalized Privacy Budget Allocation, PPBA)算法, 主要内容如下.

(1)对基于概率图模型的贝叶斯网络算法进行优化, 引入最大支撑树和最大权重值, 减少指数机制挑选属性关系对的搜索空间, 避免敌手进行多次查询对比分析, 泄露隐私信息. 提高数据可用性和安全性.

(2)依据动态权重值确定贝叶斯网络中低维属性集合敏感性由大到小的排序. 受文献[11-13]启发, 根据不同用户数据可用性与安全性需要, 个性化设置隐私预算分配比值常数 $q$ ,为不同敏感性的属性集合合理分配差分隐私(Laplace^[10])噪声.

(3)理论证明所提出的PPBA算法满足 $\varepsilon $ -差分隐私, 并在真实数据集上进行性能评估. 实验结果表明能够满足数据可用性与安全性个性化需求, 同时降低了时间复杂度.

2 相关工作

数据独立发布算法和数据相关发布算法是主要的2类面向高维数据发布的差分隐私算法. 独立发布算法的典型代表是PriVew^[14],该算法假设所有属性都是相互独立的,这在真实数据集中是不存在的, 且缺少正式的推理机制. 而PrivBayes算法^[5]、加权贝叶斯网络算法^[6]、联合树算法^[7]是典型的数据相关发布算法.

PrivBayes算法利用指数机制挑选属性关系对形成贝叶斯网络, 对联合分布概率进行推理, 存在候选空间较大, 数据可用性和安全性得不到保障的问题. 文献[6]对贝叶斯网络进行优化, 利用最大权重值提高贝叶斯网络推理的准确性, 但仍然存在挑选属性关系对候选空间较大的问题. 文献[7]通过指数机制构造Markov网, 引入高通滤波技术缩减指数机制搜索空间. 并结合相应的后置技术对Markov网分割来获得完全团图, 生成满足差分隐私的联合树, 利用联合树中各个团后置处理之后的联合分布表合成最终的高维数据. 文献[5-7]在高维数据相关发布得到广泛的应用, 但在面对不同数据机构对于数据安全性与可用性的个性化需求, 缺少个性化的隐私预算分配策略.

针对不同数据类型关于隐私预算分配问题, 为了兼顾数据安全性与可用性的效率, 文献[11]以差分隐私保护结合主流决策树分类方法, 提出等差分配隐私预算的方式, 改善决策树的分类准确率. 文献[12]针对树索引结构提出等差数列分配和等比数列分配两种方式. 避免对树的某一层分配过小, 数据可用性过低; 分配过大, 不能对这层数据提供足够安全保障的问题.

3 基础知识

本节内容主要对面向高维数据发布的个性化差分隐私算法所使用的贝叶斯网络、差分隐私概念进行说明.

3.1 贝叶斯网络

文章在论述过程中涉及较多数学符号, 为了更好地对下文相关内容进行解释, 给出相关符号定义, 如表1所示.

定义1. 贝叶斯网络. 贝叶斯网络 $N$ 为一个有向无环图, $N$ 中每一个节点代表高维数据集D中一个字段属性, 如果 $N$ 中两个属性节点之间存在着直接依赖关系, 则两个属性字段节点之间用一条弧(或有向边)直接相连. 贝叶斯网络 $N$ 使用(属性字段节点, 属性字段节点的父节点集合)对来表示.

通过挑选属性间的依赖关系, 实现高维数据的维度转换, 构建贝叶斯网络进行联合分布的推理. 通过例子解释说明, 高维数据集属性集合为 $A{{{r}}_1}$ , 有A、B、C、D共4个属性, 未进行维度转换形成贝叶斯网络时, 其联合分布的计算如下式所示:

$\begin{split} \Pr [Ar_1] =& \Pr [A] * \Pr [B|A] * \Pr [C|A,B]\\ & * \Pr [D|A,B,C] \end{split}$

(1)

若在属性依赖关系的挑选中使用最大父节点个数值即度值为2的贝叶斯网络算法对该数据集进行处理, 形成如图1所示4个属性字段节点构成的2度贝叶斯网络图.

则该贝叶斯网络用4个相对独立的低维属性集合 $(A,\emptyset )$ , $(B,\{ A\} )$ , $(C,\{ A,B\} )$ , $(D,\{ A,C\} )$ , 来表示, 其中联合分布 ${\Pr _N}[A{r_1}]$ 的计算如式(2)所示.

$\begin{split} {{{\Pr }_N}[A{r_1}]} = &\Pr [A]*\Pr [B|A]*\Pr [C|A,B]\\ &{*\Pr [D|A,C]} \end{split}$

(2)

未进行维度转化处理之前该数据集属性之间存在6种属性关系, 当使用2度贝叶斯网络算法之后降低到5种属性关系. ${\Pr _N}[A{r_1}]$ 相比 $\Pr [A{r_1}]$ 在数据量较多的情况下具有更低的计算复杂度, 为多个相对独立的低维属性集合加入更少的噪声.

3.2 差分隐私

差分隐私保护技术通过向原始数据集添加满足差分隐私的噪音生成邻近数据集, 使得原始数据集与邻近数据集在查询输出中具有概率不可区分性.

定义2. $\varepsilon $ -差分隐私^[10]. 对于任意两个相邻数据集 ${D_1}$ 和 ${D_2}$ , 它们之间相差最多为一条记录, 若一个随机函数A满足 $\varepsilon $ -差分隐私保护, $R{{ange}}(A)$ 表示随机函数 $A$ 的取值范围, 则对于所有的 $S \subseteq R{{ange}}(A)$ 有:

${\rm{Pr}}[A\left( {{D_1}} \right) \in S] \le {e^\varepsilon }{\rm{Pr}}[A({D_2}) \in S]$

(3)

其中, $\Pr [E]$ 表示事件E的披露风险, $\varepsilon $ 为隐私预算参数, 代表了差分隐私保护水平, 其值越小, 不可区分性越大, 隐私保护级别越高.

定义3. 敏感度^[10]. 敏感度是由函数本身决定的, 不同函数具有不同的敏感度, 敏感度过低会使发布数据集的安全性得不到保障, 敏感度过高则使发布数据集的发布结果实用性降低.

给定F是将一个数据集映射到一个固定大小实数向量的函数, 那么函数F的敏感度为:

$S(F) = \max {\left\| {F({D_1}) - F({D_2})} \right\|_1}$

(4)

其中, ${D_1}$ 和 ${D_2}$ 为任意两个邻近数据集, 二者仅相差一个数据元组.

为了在给定的隐私预算内, 将全部隐私预算合理分配到多个相对独立的低维属性集合中, 使整个数据发布过程中满足差分隐私, 可以利用差分隐私的序列组合性质.

性质1. 差分隐私序列组合性^[11]. 给定数据集 $D$ ,相互独立的差分隐私随机算法 ${A_1},{A_2},\cdots,{A_i}$ 分别满足 ${\varepsilon _i}$ -差分隐私, 其中 $1 \le i \le d$ , 则序列组合 $\{ {A_1},{A_2},\cdots,{A_i}\} $ 满足 $\varepsilon $ -差分隐私, 其中 $\varepsilon =\displaystyle \sum\limits_{i = 1}^d {{\varepsilon _i}} $ .

定义4. 互信息函数. 1948年香农提出信息熵^[14]的概念, 属性之间互信息I的大小代表属性之间的关联程度. 高维数据集D属性节点X与Y之间的互信息I如式(5)所示.

$\begin{split} I(X:Y) =& \sum\limits_{x \in dom(X)} {\sum\limits_{y \in dom(Y)} {P(X = x,Y = y)} } \\ & * \log \frac{{P(X = x,Y = y)}}{{P(X = x)P(Y = y)}} \end{split}$

(5)

其中, 满足差分隐私的噪音机制主要有指数机制、Laplace机制.

命题1. 基于互信息函数的指数机制. 指数机制^[10]主要用于处理输出结果为非数值型结果. 在维度转换过程中, 属性节点的关联程度作为指数机制挑选属性关系对的依据, 打分函数为属性间的互信息函数I, 其中 $\Delta I(X:Y)$ 为互信息函数I的敏感度, 以正比于 $\exp $ $ \left( {\dfrac{{\varepsilon I(X:Y)}}{{2\Delta I(X:Y)}}} \right)$ 的概率挑选出具有最大依赖关系的维度属性, 组成多个满足 $\varepsilon $ 差分隐私的相对独立的低维属性集合. 其中文献[5]中给出了维度转换过程中互信息敏感度的计算方法, 见式(6); 由于在指数机制挑选过程中, 除挑选属性关系对外无其它隐私消耗, 由差分隐私组合性质^[11], 该过程满足对应 $\varepsilon $ -差分隐私.

$\Delta (I(X:Y)) = \frac{2}{n}\log \frac{{n + 1}}{2} + \frac{{n - 1}}{n}\log \frac{{n + 1}}{{n - 1}}$

(6)

命题2. 基于联合分布的拉普拉斯机制. 拉普拉斯机制^[11]通过Laplace分布产生噪声扰动真实值达到差分隐私保护. 在贝叶斯网络中对多个相对独立的低维属性集合, 计算其联合分布 $P$ . $P^* = P + Z$ 为向其联合分布概率中添加拉普拉斯噪音 $Z$ , 其中 $\Delta f$ 为联合分布函数敏感度, ${\rm{Z}} \sim Lap(\Delta f/\varepsilon )$ 为服从尺度参数 $\Delta f/\varepsilon $ , 方差为 $2\Delta {f^2}/{\varepsilon ^2}$ 的Laplace分布. 由于在该过程中除为联合分布添加拉普拉斯噪音外无其它隐私消耗, 由差分隐私组合性质^[11]满足对应 $\varepsilon $ 值的差分隐私.

4 PPBA算法 4.1 最大支撑树

本节对最大支撑树的定义和构建过程进行解释说明, 通过最大支撑树限制指数机制挑选属性关系对的候选空间.

命题3. 最大支撑树. 利用高维数据属性之间的互信息得到的一种树状网络结构, 通过依次计算两两属性间的互信息, 只保留与该属性具有最大互信息的属性之间的无向边, 完成最大支撑树的建立. 根据最大支撑树减少挑选属性关系对的候选空间, 确定贝叶斯网络度值 $K$ .

算法1. 最大支撑树

输入: Data D

输出: $\scriptstyle VT$

1. Initialize: $\scriptstyle T = \emptyset $ , $\scriptstyle VT = \emptyset $ ;

2. ①for $\scriptstyle i$ =1 to $\scriptstyle d$

for $\scriptstyle j$ = 1 to $\scriptstyle d$ and $\scriptstyle j \ne i$

Compute $\scriptstyle I({X_i},{X_j})$ , add $\scriptstyle I({X_i},{X_j})$ to $\scriptstyle T$

②Select Max $\scriptstyle I({X_i},{X_j})$ , add $\scriptstyle ({X_i},{X_j})$ to $\scriptstyle VT$ ;

3. Return $\scriptstyle VT$ ;

根据算法1输出的 $V_T$ 集合, 其中 $VT$ 集合用于存储最大支撑树的无向边 $({X_i},{X_j})$ , 以图1为例将图中有向边转化为无向边, 由连接关系可知A、B、C、D四个属性节点无向边个数分别为3、3、2、2其中最大值为3, 则选取K值为3.

4.2 个性化比例分配

本节内容主要对个性化比例分配方法所涉及的敏感性排序和比例分配的计算过程进行解释.

(1)依据动态权重值对低维属性集合进行敏感性排序

在文献[6]中分别给出了 $CM$ 、 $WV$ 、 $DWV$ 值的计算方法, 根据文献[6]中对属性节点动态权重值的定义, 动态权重值可以很好地代表属性节点在贝叶斯网络中的重要性, 重要性越高, 对于贝叶斯网络精确度和数据集的可用性影响越大, 该属性值隐私泄露对数据集的安全性影响越大. 故选取动态权重值作为敏感性的衡量依据.

假设图1中各属性 $CM$ 值如表2中所示, 则由文献[6]的计算方法, 对图1中4个属性权重值计算结果如表2所示.

根据动态权重值大小进行排序, 则属性节点的敏感性排序为A、C、B、D.

(2) 个性化比例分配计算

高维数据集经贝叶斯网络处理之后, 将数据集划分为 $d$ 个相对独立的低维属性集合, 依据属性节点的动态权重值对低维属性集合进行敏感性由大到小排序, 根据隐私预算分配策略将总的隐私预算合理分配到每个低维属性集合. 通过个性化设置分配比值常数 $q(q > 1)$ , 从敏感性最高的低维属性集合起, 使该节点低维属性集合与前一个敏感性更高的低维属性集合分配的隐私预算大小比值为常数 $q\;(q > 1)$ , 从而将隐私预算 $\varepsilon $ 划分为 ${\varepsilon _1},{\varepsilon _2},\cdots,{\varepsilon _d}$ 分别分配至 $d$ 个低维属性集合.

由图1中属性节点的低维属性集合敏感性由大到小的排序为A、C、B、D. 总隐私预算 $\varepsilon $ 大小, 根据需要设置的比值常数为 $q\;(q \ge 1)$ .

由等比数列性质式(7)、式(8):

$\varepsilon = \sum\limits_{i = 1}^d {{\varepsilon _i}} = \frac{{{\varepsilon _1}\left( {1 - {q^d}} \right)}}{{1 - q}};q > 1$

(7)

$\varepsilon = \sum\limits_{i = 1}^d {{\varepsilon _1}} d;q = 1$

(8)

得:

${\varepsilon _1} = \frac{{\varepsilon (1 - q)}}{{1 - {q^d}}};q > 1$

(9)

${\varepsilon _1} = \frac{\varepsilon }{d};q = 1$

(10)

${\varepsilon _i} = {\varepsilon _1}{q^{d - 1}};q \ge 1$

(11)

取 $\varepsilon $ =0.5时, 分别设 $q$ 值为1、1.1、1.3, 则A、B、C、D各属性节点分配的 $\varepsilon $ 值由式(9), 式(10)计算结果如表3所示.

由以上分析和表3可知, 当给定总的隐私预算和低维属性集合按敏感性由高到低的排序, 用户只需调整 $q$ 值, 就可以改变隐私预算的分配方式. 当 $q = 1$ 时, 每个低维属性集合分配的隐私预算相同, 即均匀分配隐私预算. 当 $q > 1$ 时, 按低维属性集合排序, 每个集合分配的隐私预算以 $q$ 倍增加, 随着 $q$ 值的增加, 越重要的低维属性集合分配的隐私预算越小, 对应的保护强度越高, 数据的可用性则相应降低. 不难理解只要稍微改变 $q$ 值, 就可以改变隐私预算分配方式.

4.3 PPBA算法实现

本节描述PPBA算法的具体实现细节如算法2.

算法2. PPBA 算法

输入: $\scriptstyle D$ 、 $\scriptstyle K$ 、 $\scriptstyle q$ 、 $\scriptstyle\varepsilon $

输出: $\scriptstyle N$ 、 $\scriptstyle D^*$

1. Initialize: $\scriptstyle N$ = $\scriptstyle\emptyset $ , $\scriptstyle V$ = $\scriptstyle \emptyset $ ;

2. Select $\scriptstyle{X_1}$ ; add $\scriptstyle{X_1}$ to $\scriptstyle V$ ;add ( $\scriptstyle{X_1}$ , $\scriptstyle\emptyset $ ) to $\scriptstyle N$ ;

3. ① for $\scriptstyle i$ =2 to $\scriptstyle d$

② Initialize $\scriptstyle\Omega $ = $\scriptstyle\emptyset $ ;

③ for 每一个属性字段 $\scriptstyle X \in A{\rm{r}}/V$ , 并且

④ add $\scriptstyle (X,M)$ to $\scriptstyle\Omega $

⑤ end for

⑥ 从 $\scriptstyle\Omega $ 中选择使 $\scriptstyle\exp (\frac{{{\varepsilon _i}I({X_i},{M_i})}}{{2\Delta I({X_i},{M_i})}})$ 最大的 $\scriptstyle({X_i},{M_i})$ ; add $\scriptstyle({X_i},{M_i})$ to $\scriptstyle N$ ;add $\scriptstyle {X_i}$ to $\scriptstyle V$ ;

⑦ end for

4. Return $\scriptstyle N$ ;

5. 依据 $\scriptstyle N$ , 计算低维属性集合属性节点的 $\scriptstyle DWV$ 值;

6. 根据 $\scriptstyle DWV$ 值, 将低维属性集合敏感性由大到小排序, 计算为每个集合分配的 $\scriptstyle{\varepsilon _i}$ 值

7. ① for $\scriptstyle i$ =1 to $\scriptstyle d$ do

② Add $\scriptstyle{\lambda _i}{\rm{ = }}\frac{{\Delta f}}{{{\varepsilon _i}}}$ to $\scriptstyle P({X_i}|{M_i})$ ;

③ return $\scriptstyle P*({X_i},{M_i})$ ;

④ end for

8. Return $\scriptstyle D^*$

PPBA算法主要分为两个部分, 1–4步为算法第一部分, 实现满足 $\varepsilon /2$ -差分隐私的贝叶斯网络. 由最大支撑树确定贝叶斯网络的度值 $K$ , 第2步选择具有最大权重值的属性节点作为贝叶斯网络的首节点. 第3步以互信息函数为满足 $\varepsilon /2$ -差分隐私指数机制的打分函数, 从属性字段集合中选择d–1个低维属性集合对加入贝叶斯网络 $N$ , 其中 $V$ 用于存储属性节点, $\left( \begin{gathered} {{V}} \\ {{K}} \\ \end{gathered} \right)$ 表示 $V$ 的所有子集元素个数为 $\min (K,|V|)$ . 第4步返回满足差分隐私的贝叶斯网络 $N$ .

算法第2部分, 合成满足 $\varepsilon $ -差分隐私的发布数据集. 5–7步根据数据可用性和安全性需求设置 $q$ 值, 为每个属性集合分配满足 $\varepsilon /2$ -差分隐私Laplace机制的隐私预算. 为属性节点 ${X_i}$ 的条件分布 $P({X_i}|{M_i})$ 加入服从Laplace分布的噪音, 得到 $P*({X_i}|{M_i})$ . 第8步根据 $P*({X_i}|{M_i})$ 形成原始数据集的近似联合分布, 抽样合成满足 $\varepsilon $ -差分隐私的合成发布数据集 $D^*$ .

4.4 满足差分隐私证明

证明. 在PPBA算法中, 根据命题1和命题2在指数机制挑选属性关系对和对条件分布添加拉普拉斯噪音的过程中由差分隐私序列组合性质^[11]分别满足 $\varepsilon /2$ -差分隐私保护, 其它行为不会产生额外的隐私预算. 根据差分隐私组合性质中的序列组合性^[11], 证得PPBA算法满足 $\varepsilon $ -差分隐私.

5 实验与分析

根据实验测试结果, 对比分析PPBA算法、加权PrivBayes算法、PrivBayes算法的数据可用性、数据安全性与可用性之间个性化平衡需求的实验以及算法时间性能3个方面.

5.1 实验环境

实验中, 采用美国UCI (University of California,Irvine)所提供的机器学习库中的成人数据集, 该数据集由美国人口普查数据组成, 共计32561个元组. 在该数据集中一共选取了10个属性字段: Age, Workclass, Educatio, Maritalstatus, Race, Occupation, Relationship, Sex, Native, Country, Income. 在实验之前将数据集划分为测试数据集和训练数据集, 并对数据集做删除缺省值, 属性离散化等数据预处理操作.

实验中所使用的软硬件参数如下:

(1)操作系统: Windows10;

(2)硬件参数: IntelCoreTM I5, 2.4 GHz CPU, 8 GB DDR 内存;

(3)编译环境及工具: Python3.6, Pycharm.

5.2 贝叶斯网络精确度分析

贝叶斯网络与原始数据的拟合度直接影响发布数据的可用性. 在贝叶斯网络结构学习中使用K2^[15]算法中的评分函数确定网络结构的好坏, 本实验选择K2Score函数分别对3个算法生成的贝叶斯网络进行评分, 评分越高, 贝叶斯网络与原始数据拟合度越高. 其中由于K2函数公式特性计算网络评分值均为负值. 实验分别选取1000、5000、10000、15000、20000、25000、30000大小数据集对比3个算法生成的贝叶斯网络的精确度, 结果如图2所示.

从图2可以看出随着数据集不断增大, PPBA算法生成的贝叶斯网络的精确性高于PrivBayes算法, 原因是随着数据集不断增大, 属性维度之间的依赖关系越来越复杂, 相较于加权PrivBayes算法和PrivBayes算法, PPBA算法利用最大支撑树, 将指数机制属性关系对的挑选空间控制在较优的范围, 提高贝叶斯网络的精确度, 在数据集不断增大, 属性关系越来越复杂的情况下, 优势更为明显.

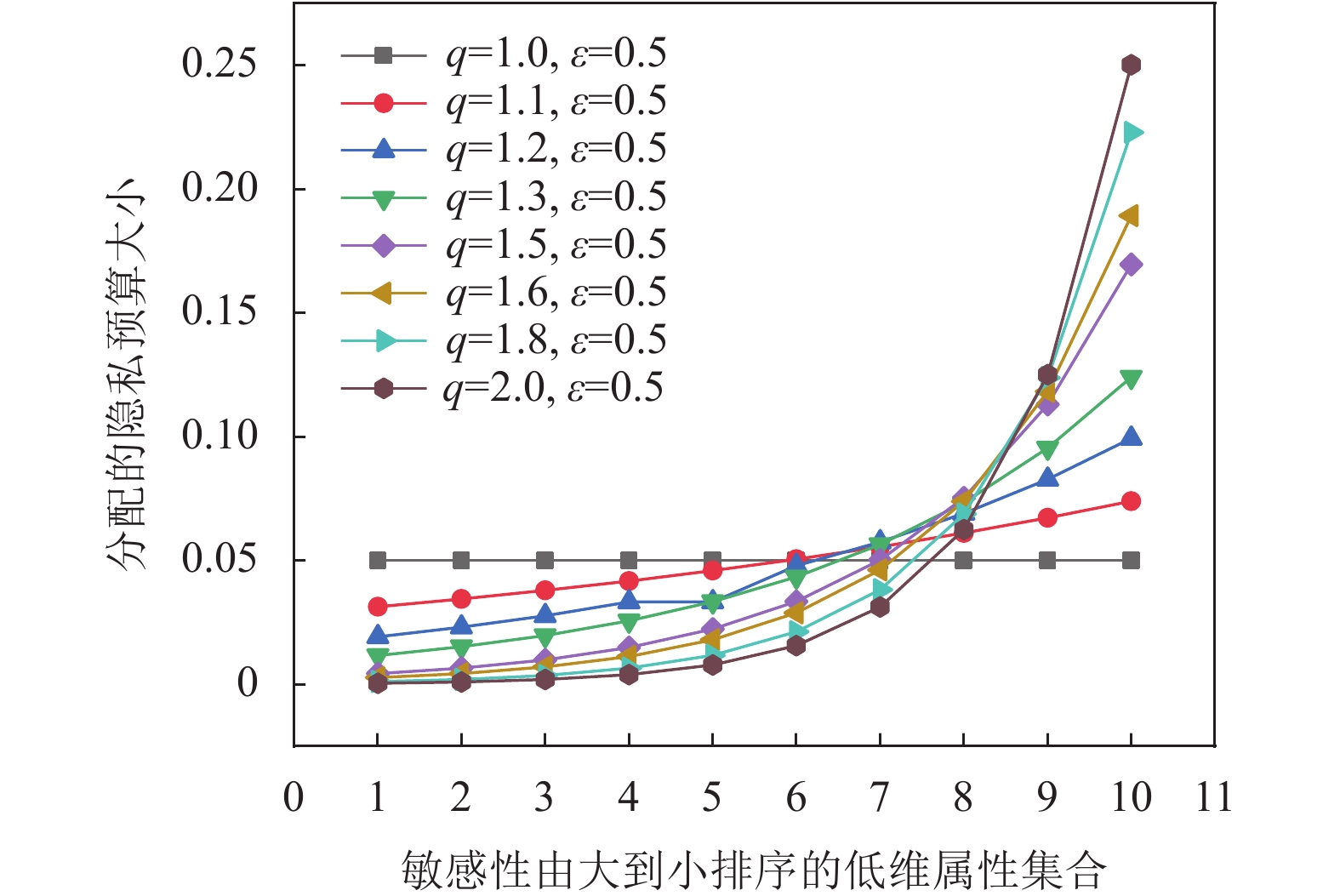
5.3 个性化分配隐私预算下数据可用性与数据安全性分析

PPBA算法将实验数据集低维属性集合按敏感性由大到小排序, 取q值大小分别为1.0、1.2、1.3、1.5、1.6、1.8、2.0. 观察取不同q值下, 将 $\varepsilon = 0.5$ 的隐私预算分配给低维属性集合, 结果如图3所示. 图3横坐标为按敏感性由大到小进行排序的低维属性集合的属性节点, 1为敏感性最高的低维属性集合的节点, 以此类推. 从图3看出, 在q值为1.0时各属性集合分配均等的隐私预算. 随着q值不断增大, 越敏感的属性集合分配的隐私预算越小, 对其隐私保护强度越大, 反之, 敏感性越小属性分配的隐私预算越大, 隐私保护强度越小. 从而实现隐私预算合理分配.

发布数据集所需的可用性与安全性之间的个性化平衡是衡量隐私预算分配优劣极重要指标. 选取训练数据集大小分别为1000、5000、10000、15000、20000、25000、30000的数据, 使用加权PrivBayes ( $\varepsilon {\rm{ = 1}}{\rm{.0}}$ )算法, PrivBayes ( $\varepsilon {\rm{ = 1}}{\rm{.0}}$ )算法, 以及 $q$ 取值1.0、1.1、1.2、1.3、1.5下的PPBA ( $\varepsilon {\rm{ = 1}}{\rm{.0}}$ )算法生成满足 $\varepsilon $ -差分隐私的合成发布数据集. 使用以上算法生成的合成发布数据集训练SVM分类模型, 利用SVM分类模型^[16]对测试数据集进行测试. 选取训练得到的SVM模型分类器对测试数据集中“Sex”属性进行分类. SVM分类的结果以及 $q$ 值分别选取1.0、1.1、1.3、1.5时通过Laplace方差计算隐私损失所得的隐私保护强度结果分别如图4、图5所示. 从图4看出 $q$ 值逐渐增大, 在数据集不大的情况下, 会出现PPBA算法SVM准确率低于加权PrivBayes算法和PrivBayes算法的现象, 但随着数据集的不断增大, PPBA算法的分类准确率均高于加权PrivBayes算法和PrivBayes算法, 更进一步的说明PPBA算法更适用于高维数据集的情况下. 从图5看出 $q$ 值越大, 隐私保护强度越高. 结合图4、图5, 根据用户对发布数据集安全性与可用性的需求, 当用户数据集元组大于15000的情况下, 对SVM分类准确率要求为80%与82%之间, 但同时要求隐私保护强度不低于0.001%与0.002%之间, 根据图4, $q$ 取值1.2可以达到数据可用性与安全性的最优平衡需求. 当用户对隐私要求保护强度为0.007%与0.008%之间, 数据可用性需求为79%到80%之间, 结合图4, 图5, 可个性化设置 $q$ 取值为1.5. 从而证明PPBA算法可以根据用户需要满足数据可用性与隐私保护强度之间个性化选择的平衡.

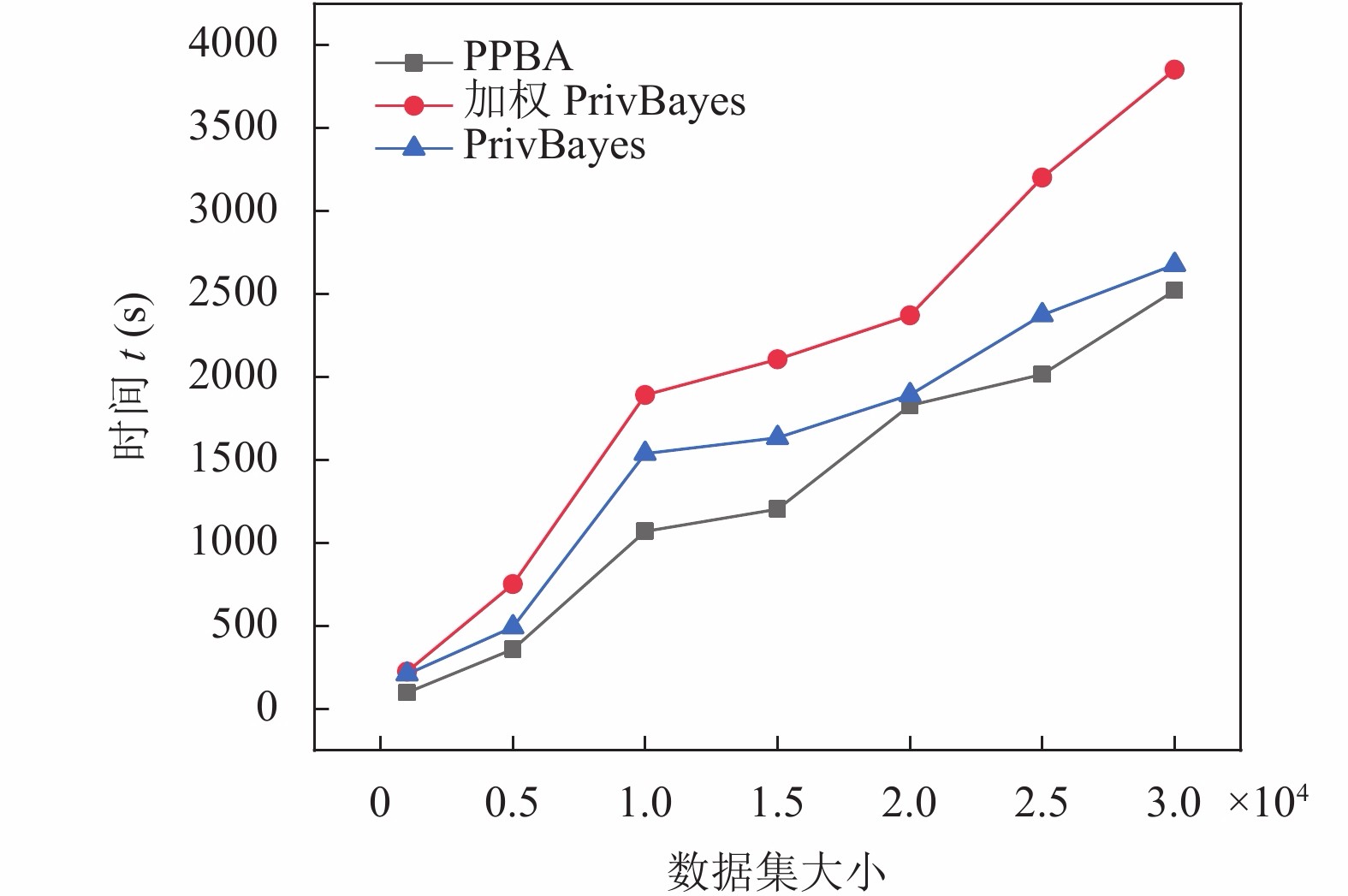
5.4 时间性能对比分析

在实验中, 将PPBA隐私保护算法( $\varepsilon {\rm{ = 1}}{\rm{.0}}$ , $q$ =1.0)、加权PrivBayes隐私保护算法( $\varepsilon {\rm{ = 1}}{\rm{.0}}$ )和PrivBayes隐私保护算法( $\varepsilon {\rm{ = 1}}{\rm{.0}}$ )在合成发布数据集过程中, 按照训练数据集由小到大进行运行时间对比分析. 由于加权PrivBayes隐私保护算法、PrivBayes隐私保护算法随机生成贝叶斯网络, 运行时间具有不确定性, 实验选择每个数据集下运行10次取平均值的方式衡量时间性能. 对比分析结果如图6所示, PPBA算法运行时间相对PrivBayes算法、加权PrivBayes算法时间更短, 究其原因PPBA算法利用属性节点权重值确定首节点, 最大支撑树确定最大父节点个数K值, 减少属性关系候选空间, 避免K值过大, 内存资源的浪费, 具有更优的时间性能. 但由于实验计算机性能有限, 数据预处理工作量大等问题, 整体耗时较长, 实验结果有待改进.

6 总结与展望

面向高维数据隐私发布, 不同数据发布用户对于数据安全性和可用性的个性化需求, 本文提出个性化差分隐私预算分配算法(PPBA), 通过最大权重值和最大支撑树, 降低属性关系对的挑选空间, 构建更优的贝叶斯网络, 按照高维数据隐私保护强度和数据可用性间的平衡需要, 个性化设置比例常数 $q$ 值,依据集合的敏感性排序, 为低维属性集合分配合理的隐私预算, 合成发布满足差分隐私数据集. 通过实验验证PPBA算法形成的贝叶斯网络更优, 具有更低的时间复杂度, 且满足根据用户需求, 个性化实现隐私预算分配. 接下来的研究工作会围绕整个算法过程中差分隐私预算分配策略再利用, 延长隐私预算使用周期, 提高发布数据的可用性等问题进行研究.