近些年来, 深度学习已经在计算机视觉和自然语言处理等领域取得了重要的进展. 然而随着研究的深入, 模型越来越复杂, 往往需要耗费大量的训练时间和计算成本. 因此, 采用有效的训练方法是十分有必要的. 以随机梯度下降(SGD)为代表的一阶优化方法是当前深度学习中最常用的方法. 近些年来, 一系列SGD的改进算法被提出并也被广泛于应用深度学习中, 比如, 动量SGD (SGDM[1]), Adagrad[2], Adam[3]. 这些一阶优化方法具有更新速度快, 计算成本低等优点, 但是也具有收敛速度慢, 需要进行复杂调参等缺点.
通过曲率矩阵修正一阶梯度, 二阶优化方法可以得到更为有效的下降方向, 使得收敛速度大大加快, 减少了迭代次数和训练时间. 对于有着上百万甚至更多参数的深度神经网络而言, 其曲率矩阵的规模是十分巨大的, 这样大规模的矩阵的计算, 存储和求逆在实际计算中是难以实现的. 因此, 对曲率矩阵的近似引起了广泛的研究. 其中最基本的方法是对角近似, 其在实际计算中取得了较好的效果, 但是在近似过程中丢失了很多曲率矩阵的信息, 而且忽略了参数之间的相关性. 在对角近似的基础上, 一些更为精确的算法也被提出, 这些算法不再局限于曲率矩阵的对角元素, 同时也考虑了非对角元素的影响. 这些方法对曲率矩阵的研究都取得的一定了进展[4-8]. 但是如何在深度学习中更加有效地利用曲率矩阵得到更有效的算法, 仍然是应用二阶优化方法面临的重要挑战.
自然梯度下降可以被视为一种二阶优化方法, 其中自然梯度定义为梯度与模型的Fisher信息矩阵的乘积. 该方法最初在文献[9]中被提出, 其在深度学习中有着重要的应用. 文献[10]中提出了一种近似全连接神经网络中自然梯度的有效方法, 称之为K-FAC. K-FAC算法首先通过假设神经网络各层之间的数据是独立的, 将Fisher信息矩阵近似为块对角矩阵; 将每个块矩阵近似为两个更小规模矩阵的克罗内克乘积, 通过克罗内克乘积的性质可以有效计算近似后的Fisher信息矩阵及其逆矩阵. K-FAC有效地减少了自然梯度下降的计算量并取得了很好的实验效果. 这一方法也被应用到其他的神经网络中, 包括卷积神经网络[11-13], 循环神经网络[14], 变分贝叶斯神经网络[15, 16]. 通过设计K-FAC的并行计算框架, 其在大规模问题中的有效性也得到了验证[17, 18].
K-FAC算法在众多问题中都有着很好的表现, 在保持K-FAC算法有效性的前提下, 进一步降低计算成本和减少计算时间是非常值得研究的问题. 在本文中, 我们基于K-FAC算法的近似思想, 结合拟牛顿法的思想, 提出了一种校正Fisher信息矩阵的有效方法. 该方法的主要思想是先用K-FAC方法进行若干次迭代, 保存逆矩阵的信息; 在后续迭代中利用该逆矩阵以及新的迭代中产生的信息, 结合Sherman-Morrison公式进行求逆计算, 大大减少了迭代时间. 实验中, 改进的K-FAC算法比K-FAC算法有相同甚至更好的训练效果, 同时大大减少了计算时间.
1 K-FAC算法神经网络的训练目标是获得合适的参数
| ${\mathbb{E}}[ - \log p(y|x,\theta )]$ |
其中,
| $F = {\mathbb{E}}\left[ {{\nabla _\theta }\log p(y|x,\theta ){({\nabla _\theta }\log p(y|x,\theta ))^ {\rm T} }} \right]$ | (1) |
文献[10]中给出了自然梯度的定义:
考虑一个有L层的神经网络,
| $ \left\{ {\begin{array}{l} {\theta _l} = {\rm{vec}}\left( {{W_l}} \right)\\ {\cal{D}}\theta = - {\nabla _{\bf{\theta }}}{\rm{log }}p\left( {y|x,\theta } \right)\\ {g_l} = {{\cal{D}}_{{s_l}}} = - {\nabla _{{s_l}}}{\rm{log }}p(y|x,\theta ) \end{array}} \right. $ |
那么Fisher信息矩阵可以被表示为:
| $F = {\mathbb{E}}\left[ {{\cal{D}}\theta {\cal{D}}{\theta ^ {\rm T} }} \right]$ |
即为:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathbb{E}}[{\rm{vec}}\left( {{\cal{D}}{\theta _1}} \right){\rm{vec}}\left( {{\cal{D}}{\theta _1}{)^ {\rm T} }} \right]}&\cdots&{{\mathbb{E}}[{\rm{vec}}\left( {{\cal{D}}{\theta _1}} \right){\rm{vec}}\left( {{\cal{D}}{\theta _L}{)^ {\rm T}}} \right]}\\ \vdots &\ddots& \vdots\\ {{\mathbb{E}}[{\rm{vec}}\left( {{\cal{D}}{\theta _L}} \right){\rm{vec}}\left( {{\cal{D}}{\theta _1}{)^ {\rm T} }} \right]}&\cdots&{{\mathbb{E}}[{\rm{vec}}\left( {{\cal{D}}{\theta _L}} \right){\rm{vec}}\left( {{\cal{D}}{\theta _L}{)^ {\rm T} }} \right]}\end{array}} \right] $ |
因此F可以被看作一个
| $F = {\rm{diag}}\left( {{F_{11}},{F_{22}}, \cdots, {F_{LL}}} \right)$ |
然而由于每个块矩阵
| $\begin{split} {F_{ll}} =& {\mathbb{E}}\left[ {{\rm{vec}}({\cal{D}}{\theta _l}){\rm{vec}}{{({\cal{D}}{\theta _l})}^ {\rm T}}} \right] \\ =& {\mathbb{E}}\left[ {({a_{l - 1}} \otimes {g_l}){{({a_{l - 1}} \otimes {g_l})}^ {\rm T} }} \right] \\ =& {\mathbb{E}}\left[ {\left( {{a_{l - 1}}a_{l - 1}^ {\rm T} } \right) \otimes \left( {{g_l}g_l^ {\rm T} } \right)} \right] \\ \approx &{\mathbb{E}}\left[ {{a_{l - 1}}a_{l - 1}^ {\rm T} } \right] \otimes {\mathbb{E}}\left[ {{g_l}g_l^ {\rm T} } \right] \end{split} $ | (2) |
其中,
| ${({A_{l - 1,l - 1}} \otimes {G_{ll}})^{ - 1}} = A_{l - 1,\;l - 1}^{ - 1} \otimes G_{ll}^{ - 1}$ |
因此Fisher信息矩阵的逆矩阵可以被近似为:
| $\begin{split} {F^{ - 1}} =& {\rm {diag}}\left( {F_{11}^{ - 1},F_{22}^{ - 1}, \cdots ,F_{LL}^{ - 1}} \right) \\ =& {\rm {diag}}\left( {A_{00}^{ - 1} \otimes G_{11}^{ - 1},A_{11}^{ - 1} \otimes G_{22}^{ - 1}, \cdots ,A_{L - 1,\;L - 1}^{ - 1} \otimes G_{LL}^{ - 1}} \right) \end{split} $ | (3) |
为了保持训练的稳定性, 需要对克罗内克因子
| ${A_{l - 1,\;l - 1}} + {\pi _l}\sqrt \lambda I,{G_{ll}} + \frac{{\sqrt \lambda }}{{{\pi _l}}}I$ | (4) |
其中,
| ${\pi _l} = \sqrt {\frac{{{\rm{tr}}\left( {{A_{l - 1,\;l - 1}}} \right)/\left( {{d_{l - 1}} + 1} \right)}}{{{\rm{tr}}\left( {{D_{ll}}} \right)/{d_l}}}} $ |
其中,
| $\theta _l^{\left( {m + 1} \right)}\leftarrow\theta _l^{\left( m \right)}-\eta \left( {{\left( {A_{l-1,l-1}^{\left( m \right)}+{\pi _l}\sqrt \lambda I} \right)^{ - 1}}\otimes{\left( {G_{ll}^{(m)}+\frac{{\sqrt \lambda }}{{{\pi _l}}}I} \right)^{ - 1}}} \right){\nabla _{\bf{\theta }}}{h^{(m)}}$ | (5) |
其中,
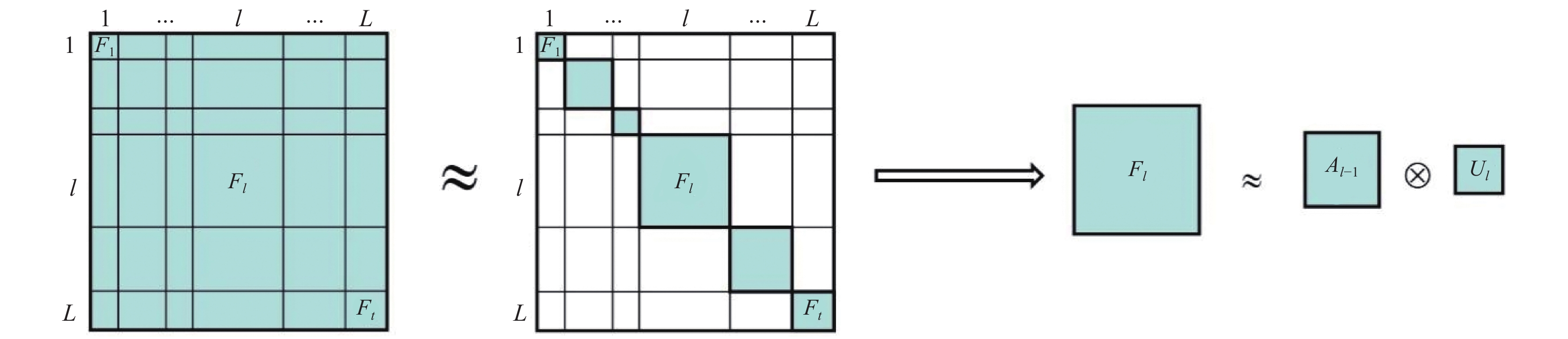
图1是K-FAC算法近似过程示意.
|
图 1 K-FAC算法近似过程示意 |
2 算法改进
在实际计算中, Fisher信息矩阵F的主对角线上的每个块矩阵的规模仍然很大, 直接对矩阵
Sherman-Morriso公式: 假设
| ${\left( {X + p{q^ {\rm T} }} \right)^{ - 1}} = {X^{ - 1}} - \frac{{{X^{ - 1}}p{q^{\rm T} }{X^{ - 1}}}}{{1 + {q^ {\rm T} }{X^{ - 1}}p}}$ | (6) |
由上述公式可以看出, 如果矩阵X的逆已知(或者很容易求), 那么利用Sherman-Morrison公式可以将矩阵的求逆运算转化为矩阵向量乘积, 从而可以减少大量的计算时间. 因此我们根据Sherman-Morrison公式, 结合拟牛顿的算法思想, 提出了一种K-FAC算法的改进算法. 在实际计算中, 每次迭代均更新逆矩阵需要很高的计算成本, 因此实验中一般设置若干次迭代更新一次逆矩阵. 在下文中, 我们用k表示逆矩阵更新的次数. 我们提出的算法主要是对K-FAC算法的求逆运算进行了进一步的改进. 其主要思想是用K-FAC 算法先进行k次求逆运算, 保存第k次求逆得到的逆矩阵信息; 后续迭代中利用该逆矩阵的信息以及在新的迭代中产生的信息, 结合Sherman-Morrison 公式进行求逆运算. 下面我们以矩阵
(1)首先, 按照K-FAC算法进行k次求逆运算, 在求出逆矩阵
(2)其次, 矩阵
| $ \left\{ {\begin{array}{l} {({u^{(k + 1)}})_i} = \sqrt {{{({A^{(k + 1)}})}_{ii}}} \\ {({v^{(k + 1)}})_i} = \sqrt {{{({G^{(k + 1)}})}_{ii}}} \end{array}} \right.$ |
那么
(3)最后, 利用Sherman-Morrison公式可以得到:
| $\begin{split} \;{{\left( {{A^{\left( {k + 1} \right)}}} \right)}^{ - 1}} \approx &\left( { {{A^{\left( k \right)}} + \alpha {u^{\left( {k + 1} \right)}}{{\left( {{u^{\left( {k + 1} \right)}}} \right)}^ {{\rm T}} }} } \right) ^{-1}\\ =& {{\left( {{A^{\left( k \right)}}} \right)}^{ - 1}} - \frac{{{{\left( {{A^{\left( k \right)}}} \right)}^{ - 1}}{u^{\left( {k + 1} \right)}}{{\left( {{u^{\left( {k + 1} \right)}}} \right)}^ {\rm T} }{{\left( {{A^{\left( k \right)}}} \right)}^{ - 1}}}}{{\alpha ^{-1} + {{\left( {{u^{\left( {k + 1} \right)}}} \right)}^ {\rm T} }{{\left( {{A^{\left( k \right)}}} \right)}^{ - 1}}{u^{\left( {k + 1} \right)}}}}\; \end{split}$ | (7) |
| $\begin{split} {{\left( {{G^{\left( {k + 1} \right)}}} \right)}^{ - 1}} \approx & \left( { {{G^{\left( k \right)}} + \beta {v^{\left( {k + 1} \right)}}{{\left( {{v^{\left( {k + 1} \right)}}} \right)}^ {\rm T} }}} \right) ^{-1}\\ = &{{\left( {{G^{(k)}}} \right)}^{ - 1}} - \frac{{{{\left( {{G^{(k)}}} \right)}^{ - 1}}{v^{(k + 1)}}{{\left( {{v^{(k + 1)}}} \right)}^ {\rm T} }{{\left( {{G^{(k)}}} \right)}^{ - 1}}}}{{\beta ^{-1} + {{\left( {{v^{(k + 1)}}} \right)}^ {\rm T} }{{\left( {{G^{(k)}}} \right)}^{ - 1}}{v^{(k + 1)}}}} \end{split}$ | (8) |
其中,
在改进的K-FAC算法中, 主要是结合Sherman-Morriso公式对Fisher信息矩阵进行了近似, 因此改进的算法在计算矩阵
| 表 1 K-FAC和改进的K-FAC算法的求逆计算复杂度对比 |
对于改进的K-FAC算法, 前
算法1. 改进的K-FAC算法
输入: 训练集T, 学习率
输出: 模型参数
初始化参数
While未达到终止条件do
if
if
根据式(2)计算因子
if
if
根据式(4)计算逆矩阵
else
计算向量
end if
end if
根据式(5)更新参数
end While
3 实验为了说明改进的K-FAC算法的有效性, 我们在常用的图像分类数据集上进行了实验. 实验中, 数据集选取的是CIFAR-10和CIFAR-100数据集[19]. 这两个数据集都是由60000张分辨率为
实验中我们采用的深度学习框架是TensorFlow, 训练的硬件环境为单卡 NVIDIA RTX 2080Ti GPU. 实验中批量大小(batch-size)设置为128, 动量为0.9, 最大迭代次数为39100, 初始学习率SGDM设置为0.03, K-FAC算法和改进的K-FAC算法设置为0.001, 学习率每16000次迭代衰减为原来的0.1. 对于K-FAC算法和改进的K-FAC算法, Fisher信息矩阵及其逆矩阵的更新频率分别为
在表2中, 我们给出了在CIFAR-10数据集上SGDM, K-AFC算法和改进的K-FAC算法的训练精度及时间比较, 其中, K-FAC算法给出了每次迭代均更新逆矩阵(1:1)和100次迭代更新逆矩阵(100:100)的实验结果. 表中第一行给出了各种算法的训练精度比较, 其余各行别给出了各种方法每次迭代的平均训练时间以及测试精度首次达到89%, 90%, 91%, 92%, 93%的训练时间, 表中最后一列给出了改进的K-FAC算法(100:100)比K-FAC算法(100:100)减少的训练时间. 因为CIFAR-100数据集和CIFAR-10数据集图像数量和分辨率相同, 这两个数据集上每次迭代的训练时间几乎相同, 所以我们仅给出了在CIFAR-10数据集上的结果, 在CIFAR-100数据集也有类似的结果.
| 表 2 SGDM, K-FAC和改进的K-FAC算法的训练精度及时间比较 |
从表2可以看出, K-FAC在不同的逆矩阵更新频率下((1:1)和(100:100))的测试精度相差不大, 但每次迭代均更新逆矩阵耗费了大量的计算时间(每次迭代平均增加了2.07 s). 结合之前的相关工作, 在本文中我们更多关注若干次迭代更新逆矩阵的实验结果. 因此, 在后文中, 我们主要基于K-FAC算法(100:100)的实验结果进行讨论.
从测试精度看, 改进的K-FAC算法与K-FAC算法相差不大. 在CIFAR-10数据集上, 改进的K-FAC算法的测试精度略低于K-FAC算法, 但在CIFAR-100数据集上, 改进的K-FAC算法的测试精度高于K-FAC算法. 从训练时间看, SGDM从89%到90%, K-FAC算法从91%到92%以及改进的K-FAC算法从从91%到92%的训练时间差距较大, 这是因为在学习率衰减之前, 测试精度在较多的迭代中变化不大, 衰减后才达到了相应的测试精度. 改进的K-FAC算法每个迭代的平均训练时间与SGDM相比, 仅增加了0.006 s, 比K-FAC减少了0.023 s. 从到达各个测试精度的时间看, 改进的K-FAC算法均比K-FAC算法减少了大量的训练时间. 比如在测试精度达到91%时, K-FAC算法比SGDM多花费了8 s, 而我们改进的K-FAC算法比SGDM减少了356 s. 从表格最后一行看, SGDM最终的测试精度达不到93%, K-FAC算法和改进的K-FAC算法都可以达到93%, 而且改进的K-FAC算法减少了237 s. 从这些结果可以看出, 我们改进的K-FAC算法可以达到与K-FAC算法相近的训练精度, 同时减少了大量的训练时间, 而且与一阶优化方法相比在速度与精度上都具有一定的优势.
图2给出了在CIFAR-10数据集上的实验结果, 分别给出了SGDM, K-FAC算法(100:100)和改进的K-FAC算法(100:100)的训练损失, 训练精度和测试精度随迭代的变化曲线. 在图中可以看出二阶优化方法(K-FAC算法和改进的K-FAC算法)收敛速度明显快于SGDM, 改进的K-FAC算法与K-FAC收敛速度相近. 从训练损失看, 所有的方法都可以达到较低的训练损失, SGDM的训练损失略高; 从精度看, 所有的方法都可以达到很高的测试精度, 我们改进的K-FAC算法在前期表现好于K-FAC.
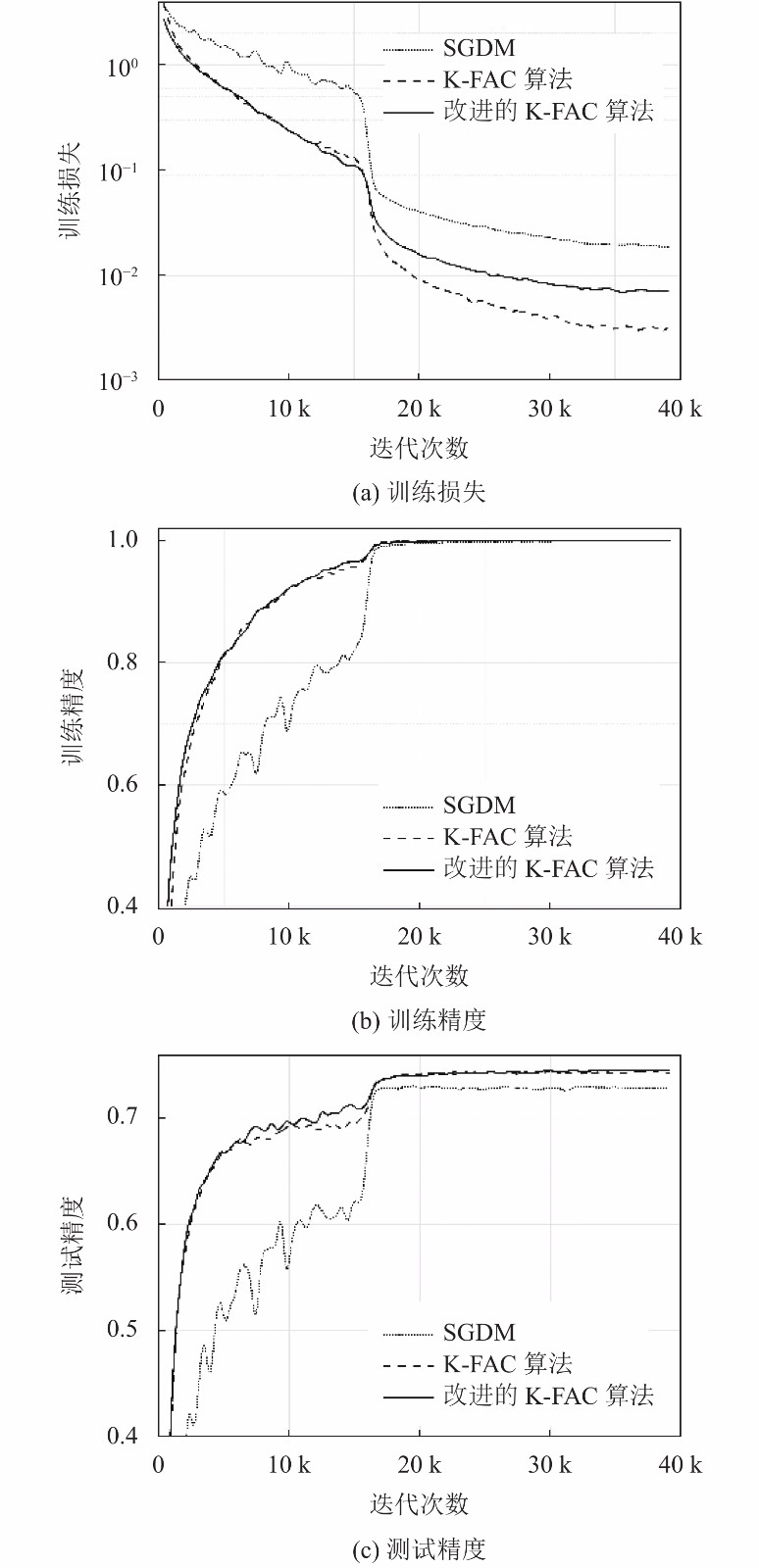
图3分别给出了SGDM, K-FAC算法和改进的K-FAC算法在CIFAR-100数据集上的训练损失, 训练精度和测试精度随迭代的变化曲线. 从图中可以看出, CIFAR-100数据集和CIFAR-10数据集有着相似的实验结果. 但从测试精度看, 改进的K-FAC算法好于K-FAC. 从这些结果我们可以看出, 我们改进的K-FAC算法与K-FAC算法相比, 有着相似甚至更好的实验效果, 说明我们提出的Fisher信息矩阵的逆矩阵进一步近似的方法是有效的.

|
图 2 CIFAR-10数据集上的实验结果 |
4 结论
在深度学习中应用二阶优化问题面临的一个重要挑战是计算曲率矩阵的逆矩阵, 由于深度神经网络拥有海量的参数导致其曲率矩阵的规模巨大而难以求逆. 在本文中, 我们基于K-FAC算法对Fisher信息矩阵的近似方法, 结合拟牛顿方法的思想, 在前期少量迭代中利用原方法训练, 后续迭代利用新计算的矩阵信息构造秩–1矩阵进行近似. 利用Sherman-Morrison公式大大降低了计算复杂度. 实验结果表明, 我们改进的K-FAC算法与K-FAC算法有着相似甚至更好的实验效果. 从训练时间看, 我们的方法比原方法减少了大量的计算时间, 与一阶优化方法相比我们改进的方法仍具有一定的优势. 但如何在深度学习中更加有效地利用曲率矩阵的信息, 得到更有效更实用的算法, 仍然是在深度学习中应用二阶优化方法面临的重要挑战.
|
图 3 CIFAR-100数据集上的实验结果 |
| [1] |
Qian N. On the momentum term in gradient descent learning algorithms. Neural Networks, 1999, 12(1): 145-151. DOI:10.1016/S0893-6080(98)00116-6 |
| [2] |
Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research, 2011, 12: 2121-2159. |
| [3] |
Kingma DP, Ba J. Adam: A method for stochastic optimization. Proceedings of the 3rd International Conference for Learning Representations. San Diego, CA, USA. 2015.
|
| [4] |
Liu DC, Nocedal J. On the limited memory BFGS method for large scale optimization. Mathematical Programming, 1989, 45(1–3): 503-528. |
| [5] |
Ollivier Y. Riemannian metrics for neural networks I: Feedforward networks. Information and Inference, 2015, 4(2): 108-153. DOI:10.1093/imaiai/iav006 |
| [6] |
Keskar NS, Berahas AS. adaQN: An adaptive quasi-Newton algorithm for training RNNs. Proceedings of 2016 European Conference on Machine Learning and Knowledge Discovery in Databases. Riva del Garda, Italy. 2016. 1–16.
|
| [7] |
Setiono R, Hui LCK. Use of a quasi-Newton method in a feedforward neural network construction algorithm. IEEE Transactions on Neural Networks, 1995, 6(1): 273-277. DOI:10.1109/72.363426 |
| [8] |
Xu DP, Dong J, Zhang CD. Convergence of quasi-Newton method for fully complex-valued neural networks. Neural Processing Letters, 2017, 46(3): 961-968. DOI:10.1007/s11063-017-9621-7 |
| [9] |
Amari SI. Natural gradient works efficiently in learning. Neural Computation, 1998, 10(2): 251-276. DOI:10.1162/089976698300017746 |
| [10] |
Martens J, Grosse R. Optimizing neural networks with kronecker-factored approximate curvature. arXiv: 1503.05671, 2015.
|
| [11] |
Grosse R, Martens J. A kronecker-factored approximate fisher matrix for convolution layers. Proceedings of the 33rd International Conference on International Conference on Machine Learning. New York City, NY, USA. 2016. 573–582.
|
| [12] |
Laurent C, George T, Bouthillier X, et al. An evaluation of fisher approximations beyond kronecker factorization. Proceedings of the 6th International Conference on Learning Representations. Vancouver, BC, Canada. 2018. 1–4.
|
| [13] |
George T, Laurent C, Bouthillier X, et al. Fast approximate natural gradient descent in a kronecker factored eigenbasis. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montreal, QC, Canada. 2018. 9573–9583.
|
| [14] |
Martens J, Ba J, Johnson M. Kronecker-factored curvature approximations for recurrent neural networks. Proceedings of the 6th International Conference on Learning Representations. Vancouver, BC, Canada. 2018. 1–25.
|
| [15] |
Zhang GD, Sun SY, Duvenaud D, et al. Noisy natural gradient as variational inference. Proceedings of the 35th International Conference on Machine Learning. Stockholm, Sweden. 2018. 5847–5856.
|
| [16] |
Bae J, Zhang GD, Grosse RB. Eigenvalue corrected noisy natural gradient. arXiv: 1811.12565, 2018.
|
| [17] |
Ba J, Grosse RB, Martens J. Distributed second-order optimization using kronecker-factored approximations. Proceedings of the 5th International Conference on Learning Representations. Toulon, France. 2017. 1–17.
|
| [18] |
Osawa K, Tsuji Y, Ueno Y, et al. Large-scale distributed second-order optimization using kronecker-factored approximate curvature for deep convolutional neural networks. Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, CA, USA. 2019. 12351–12359.
|
| [19] |
Krizhevsky A. Learning multiple layers of features from tiny images. Toronto: University of Toronto, 2009.
|
| [20] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV, USA. 2016. 770–778.
|
 2021, Vol. 30
2021, Vol. 30


