近年来, 我国普通高校数量和高校在校学生数量急剧上升, 使得高校教学质量不过关的情况越来越严重. 传统的学生管理方法和教学质量评估方法工作量大, 评判依据较为单一, 已经无法适应当前的教育体系, 大数据技术和互联网技术的发展为解决上述问题提供了有力的技术条件[1-3]. 目前国内高校普遍已经建立起自己的校园数字化管理平台, 校园数字化管理可以记录每个学生的个人行为数据, 包括日常的宿舍门禁、食堂就餐、上网记录、历史成绩等, 这些个人行为数据可以作为评估学生学业情况的重要依据[4-7].
文献[8]中提出了一种RBF神经网络学业预警算法, 建立了适用于学业预测的RBF神经网络模型, 并利用遗传算法对传统RBF网络的权重向量进行全局搜索以得到最优模型, 提升了模型的收敛速度和误差精度, 取得了不错的效果. 但文中采用的影响因素是通过专家和教师按照经验认为评定的, 评定结果的可靠性有待商榷[8]. 文献[9]利用BP神经网络进行学生成绩预测, 通过挖掘学生各科成绩之间的关系各学期历史成绩的发展趋势预测学生最终的结业成绩[9]. 国外学者Hajra也研究了在虚拟学习环境下, 采用深度人工神经网络挖掘大数据信息, 并用于学业预警[10].
本文提出了一种基于学生行为相关性分析的GA-BP学业预警算法, 运用Kendall相关性分析方法在一卡通数据库、网络数据库和历史成绩数据库中搜寻与学生学业情况相关性最强的特征数据, 确定预测网络的输入数据; 再利用相关性分析结果改进GA-BP网络, 提升算法收敛速度的同时还能避免陷入局部收敛, 建立一个综合评估学生学业情况的神经网络模型. 该算法可以综合前3年学生个人行为数据预测该生未来的学业水平, 向存在毕业困难的学生提前发出预警, 有利于学校对这类学生进行有效的监督和管理.
1 学生个人行为数据预处理学生个人行为数据主要包括一卡通数据库、网络数据库和历史成绩数据库3个数据库中的信息, 数据库中的数据一般按照时间顺序进行排列, 但其记录形式十分详细, 包含了大量的冗余信息. 例如, 在一卡通消费数据中存在商铺窗口、刷卡机号等信息, 在网络浏览数据中存在目标IP、目标端口等信息, 在历史成绩数据中存在课程名称、专业名称等信息, 因此必须对原始数据进行预处理. 本文算法的数据预处理过程主要分为去噪、拆分、统计、处理4个部分. 首先, 去噪过程主要根据数据库中的标签或标志位判断某一字段对应的记录对象, 剔除数据集中的冗余字段和无效字段; 拆分过程同样根据数据库中的标签或标志位, 将数据按照字段描述的行为信息进行拆分; 再运用统计学原理进行拆分数据的统计, 进行累加或平均等操作获得二次数据; 最后根据不同字段的数据特征按照目标要求进行二次处理, 例如按照网络访问的目标域名将学生的上网用途进行拆分, 具体流程如图1所示.

|
图 1 预处理流程图 |
1.1 一卡通数据
本文完成一卡通数据的去噪和拆分后, 按照以往一卡通数据的研究经验, 经过分类数据的二次处理得到了6个一卡通数据特征字段: 平均晨出时间、平均晚归时间(时间记录形式以24时计时法对应转换为小数形式, 例如8:30记为8.30)、早起频率(每月早8点前出宿舍的次数)、晚归频率(每月晚10点后回到宿舍的次数)、图书借阅量(每月在图书馆借阅的书物数量)、消费总金额(每月一卡通消费的总金额), 表1是一卡通数据记录示例表.
| 表 1 学生一卡通数据示例 |
1.2 网络数据
从学生上网的网络日志中按照网络用途分类得到每位学生的上网记录, 经过分类数据的二次处理得到了4个网络数据的特征字段: 游戏时长、学习时长、娱乐时长(利用网络观看视频、小说或交友聊天等)、上网总时长, 时长统计均按月为单位取平均值, 表2展示了网络数据的记录形式.
| 表 2 网络数据示例(单位: 小时/月) |
1.3 历史成绩数据
学校管理系统对于学生成绩的管理相对成熟, 因此成绩数据的预处理多数是进行关键字段的选取即可, 采用绩点的形式对学生课程情况进行统计, 分别计算了每位学生3年成绩的平均绩点、已获学分、挂科学分、挂科率, 历史成绩数据的记录形式见表3.
| 表 3 历史成绩数据示例 |
2 Kendall相关性分析
最常见的相关性分析方法有Pearson、Spearman和Kendall. Pearson相关性分析更加适用于连续数据之间的相关性分析, 而本文进行的相关性分析均为一组连续数据与一组分类数据之间的相关性分析, 例如挂科率与是否顺利毕业之间的相关性, 因此宜采用Spearman和Kendall相关性分析[11]. Spearman和Kendall都是等级相关性分析方法. Kendall相关性系数的计算需要按等级大小对一组数据进行排序[12,13]. 本文将正常毕业记为1, 未正常毕业记为0, 该组数据仅分为两个等级, 可以节省大量排序和比较的计算时间, 采用Kendall相关性分析将比Spearman相关性分析具有更快的计算速率. 因此, 本文采用Kendall相关性系数进行相关性分析.
Kendall相关性系数是用来衡量两个随机变量之间相关性的参数, 取值范围在−1~1之间, 系数值越大表明两个变量正相关关系越强, 系数值越小表明两个变量负相关关系越强[14,15]. 本文目的在于发掘每一类特征数据与学生是否能够顺利毕业的关系, 因此不考虑正负相关性的影响, 直接取Kendall相关性系数的绝对值|K|作为本文的相关性系数[16], |K|的计算方法如下:
| ${\rm{|}}K| = \left| {\frac{{C - D}}{{\sqrt {({N_3} - {N_1})({N_3} - {N_2})} }}} \right|$ | (1) |
式中, C为两组数据中具有一致性的数据对的对数, D为两组数据中不具有一致性的数据对的对数. 例如: (Xi, Yi)和(Xj, Yj)为一对数据对, 若Xi<Xj且Yi<Yj, 即表明该数据对具有一致性; 若Xi<Xj且Yi>Yj, 即表明该数据对不具有一致性. N1、N2、N3的计算方法如下:
| $\left\{ {\begin{split} {N_1} =& \sum\limits_{i = 1}^S {\frac{1}{2}} {U_i}({U_i} - 1) \\ {N_2} = &\sum\limits_{i = 1}^T {\frac{1}{2}} {V_i}({V_i} - 1) \\ {N_3} =& \frac{1}{2}N(N - 1) \\ \end{split}} \right. $ | (2) |
其中, S为第1组数据中拥有相同元素的小集合的个数, Ui为第一组数据中每个小集合中元素的个数, T为第2组数据中拥有相同元素的小集合的个数, Vi为第3组数据中每个小集合中元素的个数, N为样本的总数.
选取2014级学生在校3年的个人行为数据结合Kendall相关系数的计算方法, 得到了各项学生个人行为与未正常毕业之间的相关系数, 计算结果如表4所示.
表4中相关系数计算结果表明, 挂科率、挂科学分、网络学习时长、早起频率等8项个人行为与学生的毕业情况相关性很大, 相关性系数均高于0.5, 因此, 本文将选取相关性系数前8位的个人行为特征数据进行神经网络的训练和预测[17].
| 表 4 相关系数计算结果 |
3 改进GA-BP学业预警模型
BP神经网络是一种具有很强的非线性映射能力的神经网络, 理论上可以以任意精度逼近一个非线性函数[18,19]. GA算法是模拟自然界遗传机制搜索问题最优解的算法, 其搜索过程较为全面, 不易陷入局部最优[20]. GA算法和BP神经网络的结合能够补足两种算法各自的不足, 提升计算速度且避免陷入局部最优[21]. 相关性分析的结果明确了对学业情况影响最大的八个因素, 同时得到了每一个因素的相关性系数, 相关性系数与BP神经网络输入层与隐含层的权值有一定的关系. 因此, 在GA-BP算法初期快速缩小最优权值的范围可以有效提升算法的计算效率, 本文将采用相关性系数优化GA算法中种群的初始值来实现这一目的.
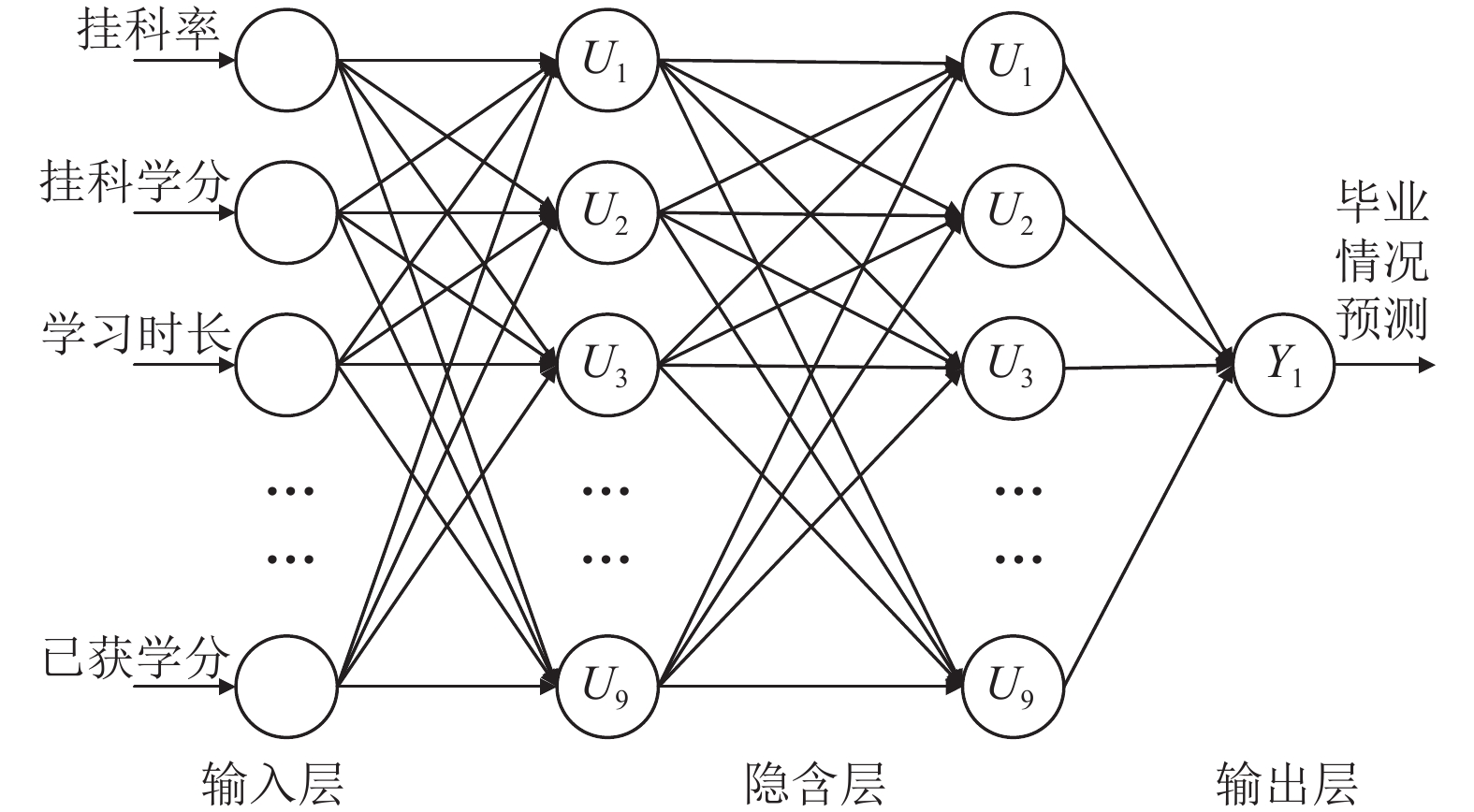
选取相关性系数较大的8个学生行为特征数据进行学生学业情况的预测, 因此神经网络将输入8维数据, 分别为挂科率、挂科学分、网络学习时长、早起频率、游戏时长、平均绩点、平均晨出时间、已获学分. 隐含层采用常用的双隐含层结构, 即隐含层数量为2层. 第1层隐含层有9个节点, 采用Sigmoid函数作为激活函数; 第2层隐含层有1个节点, 采用pureline函数作为激活函数. 输出层为学生的正常毕业情况, BP神经网络模型结构如图2所示.
|
图 2 BP神经网络模型结构图 |
GA算法用于为BP神经网络确定最优权值和阈值, 而相关性系数为GA算法确定种群的初始分布位置. 例如: 按照相关性系数从高到低排列的第一维数据为挂科率, 挂科率的相关性系数为0.732, 则在种群的初始分布中将更多的种群分布在0.732附近. 本文采用正态分布确定种群分布概率P, 计算方法如式(3)所示.
| ${P_i} = \frac{1}{{\sqrt {2*0.4\pi } }}{{\rm e}^{\left( { - \textstyle\frac{{{{(x - {\mu _i})}^2}}}{{0.32}}} \right)}}$ | (3) |
其中, x为粒子的初始值, μi第i维数据的相关性系数, 按照表4中的计算结果, μi应分别取0.732、0.707、0.685、0.632、0.601、0.589、0.576、0.532. Pi为第i维数据种群的初始分布概率. 种群数量取值为100, 每个种群粒子之间的步长间隔采用式(4)确定.
| ${L_{ij}} = \frac{{1/{P_{ij}}}}{{\displaystyle\sum\limits_{j = 0}^{100} {1/{P_{ij}}} }}$ | (4) |
其中, Lij为第i维数据第j个粒子与其前一个粒子的步长间隔. 本文输入数据维度为8, 种群数量为100, 因此i取1–8之间的整数, j取1–100之间的整数. 按照此规则设置种群中粒子的初始值能够保证初始化时种群按照期望为μi的正态分布进行分布, 增大相关性系数周围分布的初始粒子数量, 提升算法的寻优效率.
改进GA-BP神经网络的计算误差即模型的预测错误率, 是预测结果中错误预测数据数量与训练数据总量的比值. 本文根据模型的期望准确度给定模型的阈值为0.0001, 最大训练次数1000, 当计算误差低于阈值时或者训练次数超过预设最大训练次数时终止训练. 改进GA-BP学业预警模型算法流程如图3所示.
4 学业预警模型测试本次测试选取我校2014级信息与控制工程系342名学生在校3年的个人行为数据和毕业情况进行模型的训练和测试, 其中一卡通数据共625 896 124条, 网络数据共886 034 856条, 历史成绩数据共783 648条, 经过数据预处理后获得342名学生的8组个人行为特征数据和毕业情况数据, 共同构成了学业预测的原始数据集. 将原始数据集(342名)拆分为训练数据集(262名)和测试数据集(80名), 对学业预测模型进行训练和测试, 测试结果如图4所示.

|
图 3 改进GA-BP学业预警模型算法流程 |

|
图 4 测试结果统计图 |
由图4中的测试结果可以看出, 测试数据集中的80名学生的学业预测结果中, 有6名同学的预测结果与实际情况不符, 本次测试的预测准确率为92.5%.
为了验证利用Kendall相关系数改进GA-BP神经网络初始权重后的效果, 本次实验继续从数据库中调取2014级信息与控制工程系342名学生的历史数据进行网络训练. 用该组数据分别对普通的GA-BP神经网络和相关系数改进GA-BP神经网络进行训练, 分别设定网络的期望误差为0.1、0.01、0.001, 学习速率为0.01, 网络最大迭代次数为5000. 测试结果如图5所示.
在图5的测试结果中, 可以看出在相同的期望误差下, 普通GA-BP神经网络的迭代次数明显大于相关系数改进GA-BP神经网络. 因此, 在误差相同的情况下, 经过Kendall相关系数改进初始权重的GA-BP神经网络的训练速度更快.

|
图 5 普通的GA-BP与相关系数改进GA-BP的训练结果对比 |
5 结论
本文针对目前高校学生管理困难和教学评估难度大的问题, 提出了一种基于Kendall相关性分析改进GA-BP神经网络的高校学生学业预警算法. 设计了一套适用于海量教育数据分析的数据分类和二次处理方法, 将Kendall相关性分析和GA-BP神经网络相结合进行学生学业情况的预测. 利用Kendall相关性分析确定与学业情况相关性最强的8个学生行为作为预测模型的输入数据, 并采用相关系数改进GA-BP算法, 加快算法的寻优速度, 同时能够避免神经网络陷入局部收敛, 有效提高网络训练效率和预测准确率. 实验测试结果表明, 本文提出的高校学生学业预警算法的预测准确率可以达到90%以上, 能够有效对学生的学业情况进行预测和预警, 对高校学生教育的管理和学生个人的学业把控具有十分重要的意义.
| [1] |
施明毅, 杨光莹, 杜敏, 等. 基于校园行为大数据分析的学生画像系统构建探析. 中国多媒体与网络教学学报(上旬刊), 2020(4): 70-71. |
| [2] |
万生忠. 校园数字化、智能化管理可行性分析. 课程教育研究, 2020(4): 226-227. |
| [3] |
Charitopoulos A, Rangoussi M, Koulouriotis D. On the use of soft computing methods in educational data mining and learning analytics research: A review of years 2010–2018. International Journal of Artificial Intelligence in Education, 2020, 30(3): 371-430. DOI:10.1007/s40593-020-00200-8 |
| [4] |
邢晶晶. 数据挖掘技术在成绩分析及课程设置中的应用研究[硕士学位论文]. 兰州: 兰州交通大学, 2018.
|
| [5] |
史子静. 校园一卡通数据分析系统的设计与实现[硕士学位论文]. 武汉: 湖北工业大学, 2018.
|
| [6] |
郑友杰. 基于网络日志的高校学生成绩预测系统的研究与实现[硕士学位论文]. 重庆: 重庆大学, 2016.
|
| [7] |
张晓燕. 基于数据挖掘的高校学生行为分析系统设计与研究[硕士学位论文]. 西安: 西安电子科技大学, 2019.
|
| [8] |
宋楚平, 李少芹, 蔡彬彬. 一种RBF神经网络改进算法在高校学习预警中的应用. 计算机应用与软件, 2020, 37(8): 39-44. DOI:10.3969/j.issn.1000-386x.2020.08.007 |
| [9] |
翁泉源. 基于BP神经网络和Apriori算法的教学成绩预测与分析研究[硕士学位论文]. 南昌: 江西师范大学, 2018.
|
| [10] |
Waheed H, Hassan SU, Aljohani NR. Predicting academic performance of students from VLE big data using deep learning models. Computers in Human Behavior, 2020, 104: 106189. DOI:10.1016/j.chb.2019.106189 |
| [11] |
Menebo MM. Temperature and precipitation associate with Covid-19 new daily cases: A correlation study between weather and Covid-19 pandemic in Oslo, Norway. Science of the Total Environment, 2020, 737: 139659. DOI:10.1016/j.scitotenv.2020.139659 |
| [12] |
刘毓, 杨柳, 刘陆. 基于遗传神经网络的学生成绩预测. 西安邮电大学学报, 2019, 24(1): 79-84. |
| [13] |
马晓磊, 李永光, 庄红山, 等. 基于自适应神经网络的光伏输出功率预测. 信息技术, 2019, 43(11): 87-92. |
| [14] |
陈茂聪. 溢洪道流量系数计算的相关性分析——基于人工神经网络模型. 水利科学与寒区工程, 2019, 2(4): 122-124. DOI:10.3969/j.issn.1002-3305.2019.04.029 |
| [15] |
高涛, 王钊, 丁伟东, 等. 基于神经网络的驾驶行为与油耗相关性分析. 计算机与数字工程, 2017, 45(5): 803-806, 860. DOI:10.3969/j.issn.1672-9722.2017.05.003 |
| [16] |
李战春, 李之堂, 黎耀. 基于相关特征矩阵和神经网络的异常检测研究. 计算机工程与应用, 2006, 42(6): 19-21, 58. DOI:10.3321/j.issn:1002-8331.2006.06.007 |
| [17] |
温廷新, 戚磊. 基于因子分析和神经网络的定价策略研究—以手机产品为例. 现代情报, 2013, 33(2): 159-161, 170. DOI:10.3969/j.issn.1008-0821.2013.02.037 |
| [18] |
Tyagi S, Panigrahi SK. A hybrid genetic algorithm and back-propagation classifier for gearbox fault diagnosis. Applied Artificial Intelligence, 2017, 31(7–8): 593-612. |
| [19] |
曲海波, 吕粟, 张文静, 等. 幼儿小世界神经网络节点属性与影响因素的相关性分析. 生物医学工程学杂志, 2016, 33(5): 931-938, 944. |
| [20] |
李伟, 梁睿君, 宋丹. 基于NB-IoT技术和GA-BP神经网络的车位预测系统. 南京航空航天大学学报, 2020, 52(3): 454-459. |
| [21] |
谢劭峰, 赵云, 李国弘, 等. GA-BP神经网络的GPS可降水量预测. 测绘科学, 2020, 45(3): 33-38. |
 2021, Vol. 30
2021, Vol. 30


