最大割问题(max-cut problem)是指对给定的无向加权图求解出一个最大分割, 使得顶点集的互补子集I与R之间所有割边的权值之和最大. 作为图论问题中典型的组合优化问题, 最大割问题被广泛应用于图像处理、网络优化, 超大规模集成电路等诸多工程中, 研究最大割问题的有效求解算法具有十分重要的应用价值[1]. 在文献[2,3]中, Khot和Ageev证明了最大割问题是NP-Hard问题. 从理论上看, 最大割问题不存在多项式时间的精确算法. 因此发展出许多以损失精度为代价提高计算效率的启发式算法[4], 如模拟退火算法, 蚁群算法, 人工神经网络等. 基于量子效应的量子计算是以量子比特作为信息编码和存储的基本单元. Deutsch等人提出在计算方面量子计算的性能要优于电子计算[5], 选用合适的量子算法可使经典计算机中某些NP问题指数级加速[6]. 根据量子绝热模型设计的量子绝热算法以绝热定理为基础, 可对如同最大割问题、旅行商问题的布尔可满足性问题(Sat问题)进行求解[7]. 量子绝热算法核心是构造一个量子绝热系统, 控制系统哈密顿量从初始哈密顿量演化到目标哈密顿量, 通过求解目标哈密顿量的基态间接获得待求解问题的近似解[8].
文献[9]中利用Project Q编程包初步实现了量子绝热算法对最大割问题的求解程序, 并通过计算顶点数为3和6的无向图的最大割问题验证了算法的可行性. 但实验研究的对象为规模较小的最大割问题, 且并未考虑无向图中边的权值对于量子绝热算法的影响. 本文基于文献[9]的工作, 加入量子比特间耦合强度(即无向图中边的权值), 通过分析规模较大的最大割问题的求解情况, 研究量子比特间耦合强度对于量子绝热算法求解最大割问题的影响, 并且对算法改进提出一种新思路. 由于量子绝热算法演化过程需保证系统的态始终为基态, 因此需要分析最大割问题哈密顿量的期望值在演化过程中的变化情况. 利用程序绘制在演化过程中期望值变化曲线. 本文测试量子绝热算法求解6–13个顶点完全无向图的最大割问题时期望值的变化情况. 对于顶点数为8、12和13的完全无向图的最大割问题, 当耦合强度全部为1时, 量子绝热算法的期望值变化情况不符合要求. 因此调整耦合强度, 分析量子绝热算法求解最大割问题时期望值收敛对应的耦合强度范围. 由此拓展到量子绝热算法求解一般情形下8、12和13个顶点的最大割问题时的改进方法.
2 基于量子绝热算法的最大割问题求解程序 2.1 最大割问题最大割问题如图1(a)所示. 待求解的无向图有a、b、c、d、e共5个顶点, 每条边上的数字为边的权重值, 如顶点d和e之间边的权重为20. 现要求将5个顶点分为两个互补子集I和R, 使得两个子集间所有边的权重之和最大. 图1(b)为该待求解无向图对应的最优解, 5个顶点分为I={b, e}和R={a, c, d}两个子集. 红色虚线表示切割线, 黑色虚线表示两个顶点子集之间的边, 即切割边. 该最优解的切割边包含(a,b), (a,e), (b,c), (b,d), (c,e), (d,e), 对应权重值总和为2+6+8+5+4+20=45.

|
图 1 最大割问题及完全无向图示意图 |
对于求解最大割问题, 任何无向图都可以转化为完全无向图, 只需将不存在的边的权重值设为零, 使该边对最大割问题的求解没有影响. 如图1(c), 左侧为原图, 右侧为对应的完全图黑色虚线为添加边, 权值为0, 红色虚线为切割线, 更改前后最优解不变. 因此本文实验主要研究对象为完全无向图.
2.2 程序求解步骤下文以3个顶点无向图为例, 如图2(a), 说明程序求解步骤.

|
图 2 程序对3顶点无向图的求解情况 |
(1)输入待求解的完全无向图;
(2)根据无向图构造最大割问题哈密顿量Hm, n;
(3)根据量子绝热模型构造初始哈密顿量Hi,n;
(4)结合演化路径, 构造系统哈密顿量Hs,n;
(5)实现系统哈密顿量按量子算法线路演化, 求得最大割问题哈密顿量的基态|ξ(1)>, 即近似解;
(6)记录每一时刻系统哈密顿量的基态|ξ(τ)>, 绘制演化过程中期望值<ξ(τ)|Hm, n|ξ(τ)>的变化曲线, 判断是否随演化时间下降并收敛. 若不是则需调整参数重新计算.
2.3 构造量子绝热系统量子绝热算法的核心是构建一个量子绝热系统, 对应程序求解第(2)、(3)、(4)、(5)步.
第(2)步根据待求解无向图的边构造最大割问题哈密顿量. 定义量子绝热近似求解n个顶点的完全无向图最大割问题的任意一个解为|α>=|α0>|α1>…|αn–1>, 其中[8,10],
| $ |{\alpha }_{{i}}\rangle =\left\{\begin{array}{l}|0\rangle , {\alpha }_{{i}}\in I \\ |1\rangle , {\alpha }_{{i}}\in R \end{array}\right.$ | (1) |
则图2(a)对应的最优解为|0>|1>|1>.
以|α>作为基态构造最大割问题哈密顿量为[9]:
| ${H_{m,n}} = 0.5\sum\limits_{{e_{i,j}}} {{w_{i,j}}\left( {\sigma _{\textit{z}}^{(i)} \otimes \sigma _{\textit{z}}^{(j)} - {I_{{2^n} \times {2^n}}}} \right)} $ | (2) |
其中, n为待求解无向图的顶点数, ei,j表示完全无向图中的以顶点i和j为端点的边(i, j), wi,j为边(i, j)对应的权重值, 对应量子比特间的耦合强度, 泡利矩阵
| $\begin{split} {H_{m,3}} =& 0.5 * \left[ {3 * \left( {\sigma _{\textit{z}}^{(0)} \otimes \sigma _{\textit{z}}^{(1)} \otimes I - {I_{8 \times 8}}} \right) } \right.\\ & + 1 * \left( {I \otimes \sigma _{\textit{z}}^{(1)} \otimes \sigma _{\textit{z}}^{(2)} - {I_{8 \times 8}}} \right) \\ & \left. { + 2 * \left( {\sigma _{\textit{z}}^{(0)} \otimes I \otimes \sigma _{\textit{z}}^{(1)} - {I_{8 \times 8}}} \right)} \right] \\ \end{split} $ | (3) |
第(2)步根据量子绝热模型构造初始哈密顿量[9,11], 定义:
| $ {H}_{i,n}={0.5}^{n}\underset{n{\text{个}}}{\underbrace{(I-{\sigma }_{x})\otimes \cdot \cdot \cdot \otimes (I-{\sigma }_{x})}}$ | (4) |
其中, n为待求解无向图的顶点数, 泡利矩阵
| ${H_{i,3}} = {0.5^3}(I - {\sigma _x}) \otimes (I - {\sigma _x}) \otimes (I - {\sigma _x})$ | (5) |
根据量子绝热模型, 初始哈密顿量的基态应是简单且容易构造的. 经计算Hi,n的基态为
第(4)步结合上述两步, 构造系统哈密顿量[12]:
| ${H_{s,n}}(t) = p(t){H_{i,n}} + q(t){H_{m,n}}$ | (6) |
其中, 演化时间t的取值范围是[0, T], 演化路径p(t)和q(t)满足边缘条件:
| $p(0) = q(T) = 1,p(T) = q(0) = 0$ | (7) |
将式(7)代入式(6)有:
| $\begin{array}{l} {H_{s,n}}(t = 0) = 1 \cdot {H_{i,n}} + 0 \cdot {H_{m,n}} \\ {H_{s,n}}(t = T) = 0 \cdot {H_{i,n}} + 1 \cdot {H_{m,n}} \\ \end{array} $ | (8) |
边缘条件保证了系统哈密顿量Hs,n从初始哈密顿量Hi,n演化到最大割问题哈密顿量Hm,n, 使得系统的态|ξ>从Hi,n的基态演化到Hm,n的基态. 为了方便计算, 实验中采用线性路径, 设为:
| $p(t) = 1 - \frac{t}{T},q(t) = \frac{t}{T}$ | (9) |
令τ=t/T, Δτ=1/T, 可知τ的取值范围是[0,1]. 由式(6)和式(9)可得系统哈密顿量为[11,13]:
| ${H_{s,n}}(\tau ) = (1 - \tau ){H_{i,n}} + \tau {H_{m,n}}$ | (10) |
则图2(a)对应的系统哈密顿量为:
| ${H_{s,3}}(\tau ) = (1 - \tau ){H_{i,3}} + \tau {H_{m,3}}$ | (11) |
第(5)步根据量子绝热模型设置量子算法线路:
| ${U_i}(\tau ) = {e^{ - i{H_{i,n}}(1 - \tau )}},{U_m}(\tau ) = {e^{ - i{H_{m,n}}\tau }}$ | (12) |
对于图2(a), 程序在第i个Δτ时刻对所有量子比特进行一次Um(i*Δτ)和Ui(i*Δτ)运算[14], 使得系统哈密顿量Hs,3(式(11))从初始哈密顿量Hi,3(式(5))向最大割问题哈密顿量Hm,3(式(3))演化. 并在每一时刻纪录各个量子比特的状态|ξ(τ)>, 最终输出|ξ(1)>=|0>|1>|1>即为算法所求近似解.
2.4 检验演化基于量子绝热算法的最大割求解算法是以牺牲精确度为代价换取计算效率, 属于启发式算法. 量子绝热算法需要保证系统在绝热条件下演化, 程序根据量子绝热算法模拟绝热条件, 演化过程中系统的最低能级对应求解问题的最优解. 当系统哈密顿量的期望值随演化时间逐渐减小并收敛于某值, 此时的系统量子态对应于该问题的最优解, 收敛值对应于该问题的最大割值. 在系统哈密顿量演化过程中, 程序第(5)步中在每一个Δτ时刻执行完量子操作后, 纪录当前所有量子比特的状态, 即每一时刻系统哈密顿量的基态|ξ(τ)>. 结合最大割问题哈密顿量Hm, n, 计算并绘制最大割问题哈密顿量的期望值[15]<ξ(τ)|Hm, n|ξ(τ)>的变化曲线, 如图2(b). 根据量子绝热模型, 当期望值随演化时间τ减小并收敛, 则所得近似解即为最优解.
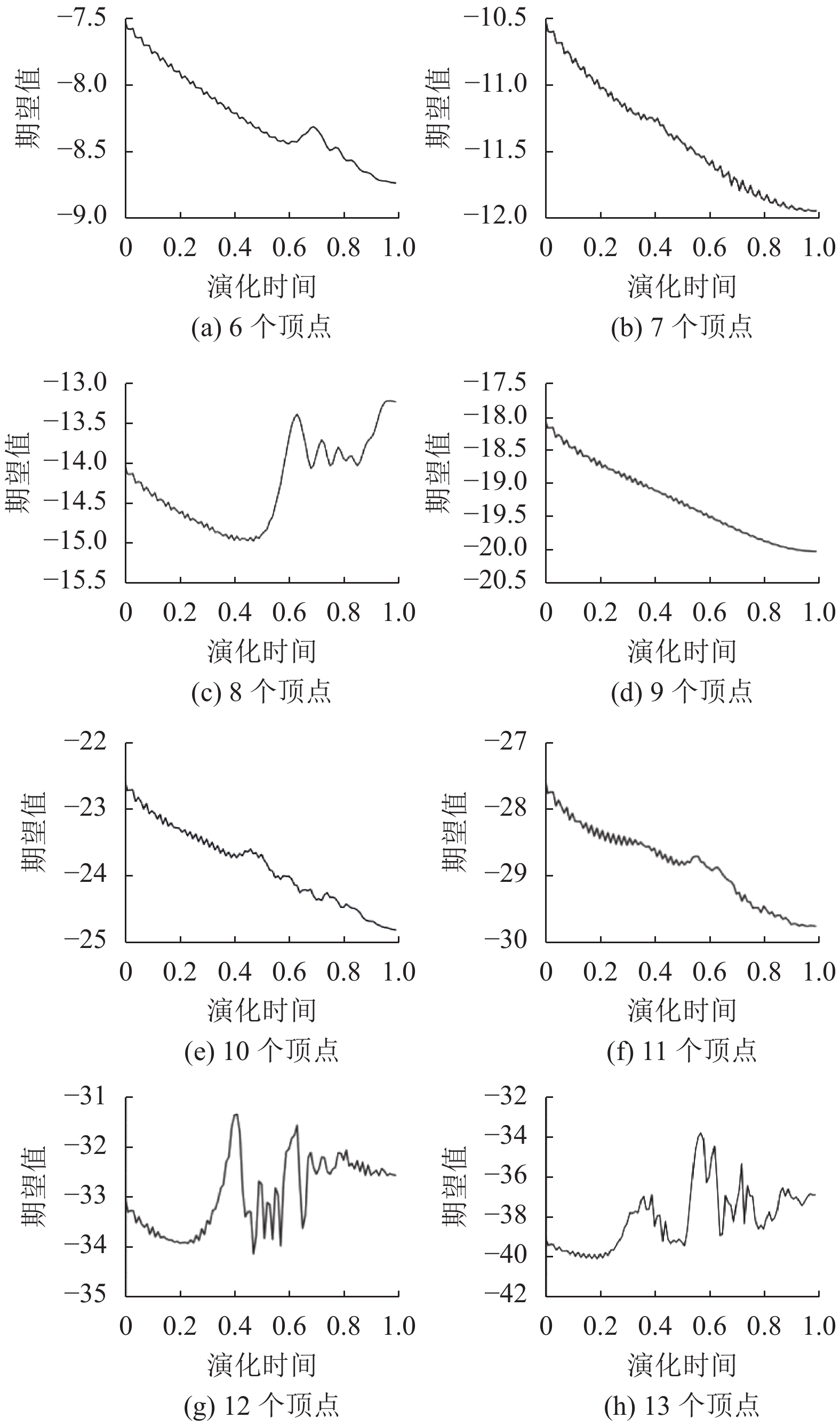
3 期望值变化曲线分析 3.1 程序对不同顶点数的完全无向图的求解情况本文测试了顶点数为6–13的完全无向图最大割求解, 最大割问题哈密顿量的期望值变化曲线如图3所示. 量子比特间耦合强度wi,j全部设置为1, Δτ取0.01. 由于完全无向图中顶点数目不同, 导致量子比特数不同, Hm, n和|ξ(τ)>的值也不同, 因此不同顶点无向图对应的期望值在任一时刻都不同.
由图3可知, 顶点数为6、7、9、10和11的完全无向图,最大割问题哈密顿量的期望值随演化时间τ逐步减小并收敛于最小值, 算法所求解即为最优解. 对于8个顶点完全无向图, 如图3(c)所示, 期望值在演化时间τ取[0, 0.5]时从初始值减小到最小值. 在演化时间τ=0.5附近开始增大, 并在τ=0.6附近到达极大值. 在0.6<τ<1范围内, 期望值在一个大于初始值的区间内振荡. 由图3(g)和图3(h)可知, 顶点数为12和13的完全无向图对应的期望值在0<τ<0.2区间内逐步减小. 期望值在0.2<τ<0.6内先增大再减小后继续增大, 其中当演化时间τ=0.4左右, 期望值达到极大值, 当演化时间τ=0.5附近, 期望值为极小值. 从演化时间τ=0.6开始, 期望值分别在–32.3和–37附近小幅度波动.
结果表明, 当顶点数较多时期望值出现不收敛的情况, 并且收敛效果越来越差. 因此需要调整实验参数, 使得顶点数为8,12和13的完全无向图对应的期望值曲线随演化时间逐步下降直至收敛.
|
图 3 不同顶点数的期望值变化 |
3.2 耦合强度对量子绝热近似求解最大割的影响
在量子绝热算法为数不多的参数中, 有一个相对重要的参数——量子比特间耦合强度. 耦合强度代表了彼此有关联的量子比特相互作用的强度. 两个量子比特间相互作用越强, 这两个量子比特越容易互相影响. 在绝热演化过程中, 系统能量的变化易受量子比特间相互作用影响, 从而影响量子绝热算法的准确率. 在求解最大割问题时, 算法中每一个量子比特对应无向图中唯一一个顶点, 因此两个量子比特间耦合强度对应了无向图中以这两个量子比特对应顶点为端点的边的权重值. 权重值越大, 耦合强度越大, 量子比特间的相互影响越强. 由于耦合强度的存在, 导致了在演化过程中系统的态受到耦合强度的影响从而偏离最低能量变化路径. 并且当最大割问题规模增加时, 量子比特数相应增加, 与任一量子比特互相耦合的量子比特数也增加, 该量子比特在演化过程中更加容易受到影响, 从而导致演化过程中系统的能量受到影响. 因此需要研究耦合强度对于量子绝热算法求解最大割问题的影响, 从而使得量子绝热算法在求解最大割问题时稍加改进.
根据3.1节所得的实验结果, 采用量子绝热算法求解最大割问题时, 当顶点数目增加时, 量子比特的数目增加, 量子比特间的相互作用情况更为复杂, 其计算最优解将会更加困难. 因此尝试耦合强度wi,j在0.7到1之间变化, 每隔0.05取值, 分析耦合强度对于所求解完全无向图期望值的影响. 根据上述条件, 求解顶点数为8, 12, 13的完全无向图的最大割问题, 变化情况如图3所示.
由图4(a)给出了不同耦合强度下8个顶点的完全无向图的求解情况. 在演化时间小于0.5时, 量子比特间的耦合强度对期望值变化没有明显的影响. 当演化时间在0.5到1之间时, 当耦合强度取0.7, 0.75和0.8时, 期望值始终处于下降趋势, 并最终收敛. 对于12个顶点的完全无向图, 不同耦合强度对期望值的影响如图4(b)所示. 演化时间取0到0.25之间时, 期望值受耦合强度的影响可忽略不计. 当演化时间大于0.5时, 相比于耦合强度的其他取值, 0.85和0.9对应的期望值曲线没有上升趋势, 且的收敛效果最好. 当顶点数增加到13时如图4(c), 期望值在演化时间取[0, 0.2]区间内不受耦合强度的影响. 演化时间在0.2到1之间变化时, 耦合强度取0.95, 期望值走势最差, 而耦合强度为0.7,0.75和0.8对应的期望值曲线始终下降并收敛.
结合图4所示的数据结果, 当完全无向图的顶点数为8和13时, 量子比特间的耦合强度取0.7, 0.75和0.8, 最大割问题哈密顿量的期望值变化趋势符合算法要求. 而对于12个顶点的完全无向图, 耦合强度取0.85和0.9时, 期望值才能较好地收敛. 综合上述结果分析, 耦合强度过高或者过低都会导致系统的态在演化过程中偏离基态, 降低算法的准确度. 并且除顶点数为12的完全无向图, 耦合强度取0.75时期望值变化效果最好. 由此提出一种改进方案, 在量子绝热算法求解最大割问题时, 为使期望值收敛得到最优解, 可将最大割问题的量子比特间耦合强度按比例映射到相应区间, 例如将12个顶点的最大割问题的耦合强度按比例映射到0.85–0.9区间内, 顶点数为8和13对应的所有耦合强度按比例映射到以0.75为中值的区间内.
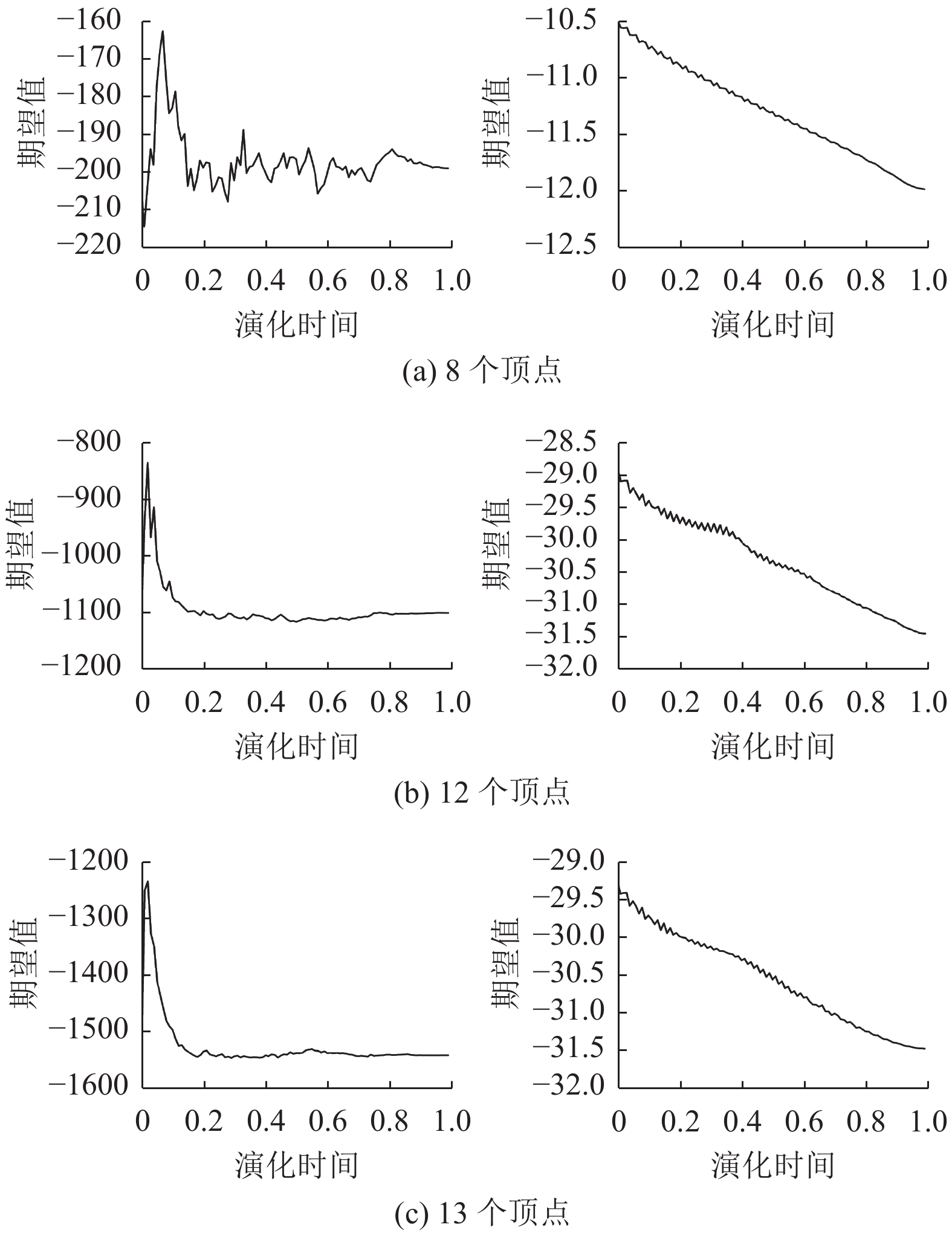
3.3 普遍情况下的完全无向图求解情况根据3.2节所得结论, 测试顶点数为8、12、13, 且每一个量子比特间耦合强度均不同的完全无向图, 期望值变化曲线如图5所示. 由于耦合强度的变化导致最大割问题哈密顿量变化, 因此耦合强度调整前后期望值曲线的起始值也发生变化.

|
图 4 不同耦合强度下期望值变化情况 |
构造一个8顶点的完全无向图, 其耦合强度为1到28依次加1的自然数列. 程序求解过程中期望值变化情况如图5(a)左图所示, 此时期望值在−200左右波动, 不满足要求. 因此调整耦合强度, 将8个顶点无向图的耦合强度映射为0.735到0.762依次加0.001的等差数列, 期望值变化情况如图5(a)右图所示. 对于顶底数为12的完全无向图, 构造耦合强度为1到66依次相差1的序列, 对应的期望值如图5(b)左图所示, 期望值先增大后减小, 不符合要求. 根据3.2节得出的结论, 将其耦合强度映射到区间[0.842, 0.908], 调整后的期望值变化如图5(b)右图所示. 同理将13个顶点对应的耦合强度(为1到78的等差数列, 期望值变化情况如图5(c)左图所示)映射到以0.75为中值的区间上, 期望值变化曲线如图5(c)右图所示. 对比可知调整前, 期望值都是先增大后减小且终值大于初值, 演化过程中系统并未一直处于基态, 算法不能给出最优解. 调整耦合强度以后, 期望值曲线明显处于下降趋势且最终开始收敛, 满足量子绝热算法要求. 由于耦合强度是按比例映射的, 对于最优解的选择没有影响, 因此调整后算法给出的解即为调整前对应的最优解.
|
图 5 耦合强度调整前后对比 |
4 结束语
本文通过编程模拟量子绝热算法求解不同顶点的完全无向图的最大割问题, 发现对于顶点数量较小的完全图, 例如3到7个顶点的情形, 所得期望值收敛, 量子绝热算法可以表现出较好的求解精确度. 当顶点数增加到8、12和13个时, 量子绝热算法所求解对应的期望值不收敛. 随着完全无向图的顶点数目增加, 量子比特间相互作用更加复杂, 造成期望值不收敛的原因也有多种可能. 可以通过调整计算步长, 演化路径, 哈密顿量等参数, 尝试使期望值趋于收敛. 本文尝试调节量子比特间耦合强度, 使多顶点的问题求解的期望值随演化时间减小并收敛, 为量子绝热算法求解较多顶点数的最大割问题提供了一个改进思路.
| [1] |
丁海军. 杨乐好. 求解最大割问题的交叉熵算法. 计算机工程与应用, 2009, 45(30): 53-56. DOI:10.3778/j.issn.1002-8331.2009.30.017 |
| [2] |
Khot S, Kindler G, Mossel E, et al. Optimal inapproximability results for max-cut and other 2-variable CSPs?. SIAM Journal on Computing, 2007, 37(1): 319-357. DOI:10.1137/S0097539705447372 |
| [3] |
Ageev AA, Kel’manov AV, Pyatkin AV. NP-hardness of the Euclidean max-cut problem. Doklady Mathematics, 2014, 89(3): 343-345. DOI:10.1134/S1064562414030235 |
| [4] |
孔树锋. 启发式算法求解最大割问题的性能分析与优化[硕士学位论文]. 广州: 华南理工大学, 2014.
|
| [5] |
Deutsch D, Jozsa R. Rapid solution of problems by quantum computation. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1992, 439(1907): 553-558. |
| [6] |
吴楠. 宋方敏. 绝热量子计算. 南京邮电大学学报(自然科学版), 2011, 31(2): 19-26. |
| [7] |
Žnidarič M, Horvat M. Exponential complexity of an adiabatic algorithm for an NP-complete problem. Physical Review A, 2006, 73(2): 022329. DOI:10.1103/PhysRevA.73.022329 |
| [8] |
段乾恒. 绝热量子计算理论研究[博士学位论文]. 长沙: 国防科学技术大学, 2014.
|
| [9] |
王富民, 倪明, 周明, 等. 量子绝热近似求解最大割问题的最优解. 计算机工程, 2020, 46(1): 25-30. |
| [10] |
Farhi E, Goldstone J, Gutmann S, et al. A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem. Science, 2001, 292(5516): 472-475. DOI:10.1126/science.1057726 |
| [11] |
Farhi E, Goldstone J, Gutmann S, et al. Quantum computation by adiabatic evolution. arXiv: quant-ph/0001106, 2000.
|
| [12] |
李华钟. 绝热量子计算理论引介. 物理学进展, 2008, 28(4): 396-400. DOI:10.3321/j.issn:1000-0542.2008.04.003 |
| [13] |
Sun J, Lu SF. On the quantum adiabatic evolution with the most general system Hamiltonian. Quantum Information Processing, 2019, 18(7): 211. DOI:10.1007/s11128-019-2313-7 |
| [14] |
Farhi E, Goldstone J, Gutmann S. A quantum approximate optimization algorithm. arXiv: 1411.4028, 2014.
|
| [15] |
Tulsi A. Adiabatic quantum computation with a one-dimensional projector Hamiltonian. Physical Review A, 2009, 88(5): 052328. |
 2021, Vol. 30
2021, Vol. 30


