随着全球金融市场的飞速发展,小微贷款成为金融机构的一项重要业务. 随着贷款空间的极速膨胀, 传统金融机构贷款业务范围正不断受到冲击, 使得互联网金融高速发展. 因此, 需要有效地控制风险手段维持行业健康发展. 大量坏账的出现将会产生类似次贷危机的事件, 对我国经济发展造成影响^[1]. 随着数据挖掘技术的逐渐发展, 其在金融领域的应用也更加完善. 机器学习技术为贷款风险预测提供了一个统一、多方面且完整的标准, 进而提高贷款分析的效率与质量.

对于贷款风险预测, 国内外已有较为丰富的研究. 传统方法主要根据相应财务指标、个人征信数据、借款意图等多方面结合, 根据专家意见形成模型. 国内外对于信用评估已有丰富的研究, 主要根据一些财务指标计算结合专家意见形成模型. Fernandes等人通过验证提出了基于Logistic回归的信用评估模型, 成为了用户信用评估的主流方法之一^[2]. 随后在国内金融环境里, 梁琪分析国内沪深上市公司失败原因, 指出主成分判别模型在风险监测和信用评估上带来很高的应用价值^[3]. 然而传统回归模型准确率偏低, 难以达到预测效果. 而今, 结合机器学习技术建模已成趋势. 基于随机森林的组合分类算法^[4]被证明在贷款风险预测算法上有着更高的精度和稳定性. 郭春桃^[5]通过比较6种中小企业信用风险预测的方法, 证明集成机器学习模型准确率高于单一模型. 贷款数据中包含年龄、性别等多类型数据, 运用Gradient Boosting方法有很好的表现. CatBoost (Category Boosting)是一种基于梯度的提升树算法, 能够很好的处理类别型特征^[6]. 其采用组合类别特征, 可有利于发掘特征之间的联系.

粒子群算法(Particle Swarm Optimization, PSO)因其较快的收敛速度和简单的算法结构而广泛应用于各大优化问题中^[7]. 种群所包含的粒子为问题的解, 通过目标函数选出每次迭代后粒子的个体最优值及种群最优值. 随后通过粒子速度v更新各个粒子的位置. 然而, PSO算法在解决多峰问题时, 容易陷入局部极值, 最终导致提前收敛. Liang等人提出了综合学习离子群(Comprehensive Learning Particle Swarm Optimization, CLPSO)算法^[8].

根据贷款信用数据复杂非线性的特点, 本文采用CatBoost模型对贷款风险进行预测. 由于CatBoost自身部分超参数可解释性较弱, 超参数将会影响模型的准确率. 本文利用综合学习粒子群(CLPSO)算法对CatBoost进行优化. CLPSO算法是一种具有优良全局搜索能力的改进粒子群算法. 在一定程度上避免了粒子群算法的局部收敛问题, 可以有效提高CatBoost贷款预测模型的精度.

1 CLPSO与CatBoost算法原理 1.1 综合学习离子群优化算法

传统粒子群算法通过自身最优和全局最优两个值来更新速度与位置, 当全局最优值陷入局部极值时, 所有粒子则容易向其学习陷入局部极值中^[9]. CLPSO算法的速度更新公式并未引入单一粒子向全局最优值学习的部分, 而是将所有粒子的 ${P_{\rm {best}}}$ 作为学习样本. 这样可以提高粒子在不同维度间的信息交换, 从而提高了种群多样性. 其中, 个体最优值即单个粒子从开始至当前时间k内找到的最优解 ${P_{\rm {best}}}$ , 全局最优值即所有粒子在当前时间内找到的最优解 ${P_{\rm {global}}}$ ^[10]. 粒子k在i时刻的速度更新公式如下所示:

$v_k^d = \omega v_{lk}^d + {c_1}{r_1}\left[ {P_{{\rm{best}}{f_k}(d)}^{\begin{array}{*{20}{c}} &{} \scriptstyle d \end{array}} - x_{lk}^d} \right]$

(1)

式中, $v_k^d$ 为粒子k在d维的速度, k为粒子编号n为粒子总数. $\omega $ 为在(0,1]的惯性权重, $v_{lk}^d$ 为上一时刻粒子k在d维的速度, ${c_1}$ 为在(0,2]的学习因子. ${r_1}$ 为在(0,1]均匀分布的随机数, $x_{lk}^d$ 为k粒子上一时刻在d维的位置. ${P_{{\rm{best}}{f_k}(d)}^{\begin{array}{*{20}{c}}&{} \scriptstyle d\end{array}}}$ 为粒子k在d维学习样本 ${f_k}(d)$ 的最优解. ${f_k}(d)$ 为根据学习概率 ${P_k}$ 选择出的学习样本. 在进行粒子寻优时, 没有向群体最佳经验学习的例子将会通过产生随机数与 ${P_k}$ 比较的方式确定学习对象. 若随机数大于 ${P_k}$ , 则 ${f_k}(d)$ 为粒子自身的最佳经验, 否则向其他例子学习. ${P_k}$ 表达式如下^[10]:

${p_k} = 0.05 + 0.45\frac{{\exp \left( {\dfrac{{5\left( {i - 1} \right)}}{{n - 1}}} \right) - 1}}{{{\rm e}^ 5 - 1}}$

(2)

根据粒子k的速度更新公式, 其位置更新公式如下:

$x_k^d = x_{lk}^d + v_k^d$

(3)

1.2 CatBoost算法

在进行特征工程时, CatBoost算法采用了独有的分类模式. 将所有特征按照贪婪策略进行整合, 计算特征的统计特性与出现频率, 并根据自身所设置的超参数产生特定的衍生字段^[11].

传统梯度下降决策树(GBDT)模型训练弱学习器时均基于相同的数据集求得模型的精度从而导致梯度估计偏差, 最终导致预测偏差^[12]. 弱学习算法如下:

$ {h}_{t}=\underset{h\in H}{\rm{argmin}}E{\left(-{g}^{t}\left(x, {\rm{y}}\right)-h\left(x\right)\right)}^{2}$

(4)

式中, ${h_t}$ 为t代弱学习器, ${g}^{t}\left(x, {{y}}\right)$ 为损失函数的梯度. 面对GBDT模型共有的预测偏移问题, CatBoost算法通过提出ordered boosting的方式计算损失函数的梯度, 从而得到无偏梯度估计. 对每个样本 ${x_i}$ , 算法通过不包含样本的训练集训练单独的模型 ${M_i}$ . 针对每个样本所获得的模型 ${M_i}$ , 算法采用求取偏差的方式得到关于样本的梯度估计, 克服了预测偏移.

在进行预测时, CatBoost采用完全平衡树作为基础预测器. 因完全平衡二叉树的对称结构, 其叶子结点索引可编码为二进制向量, 长度等于树的深度. 算法可将所有特征进行二值化用以进行模型的预测.

2 贷款风险评估模型 2.1 特征工程

本次实验数据选用国内某金融企业在2016年至2019年间的车辆抵押贷款情况, 总计数据26657条, 包含身份信息、车辆信息、社交数据、填写行为多方面总计78个特征, 其中正样本21068条, 存在贷款风险的样本5589条.

(1)缺失值处理

现实数据往往因为多种原因导致数据缺失. 实验根据数据的缺失程度对数据进行分别处理诸如车辆保险金额、申请人工作年限等缺失率大于30%的特征, 因对实验模型存在较大影响, 将其删除. 对于缺失率低于30%的特征, 将使用差补法对其进行补全. 对于连续特征如审核时间, 采取均值插补法, 以特征的中位数进行补充. 对于类型特征如职业、学历等以NAN进行补充. 对于离散特征, 如以主要手段为采用均值插补和众数插补的方式, 根据该特征其余数据预测填补. 去除缺失比例较高的特征后, 实验数据剩余57个特征.

(2)独热编码

数量大于3的类型特征通常并不存在比较关系, 但仍以0、1、2进行表示, 而实验算法可能将其数值大小进行逻辑判断. 因此将类型特征进行独热编码, 以性别为例, 将原本的单一特征转化为是否男性、是否女性两个特征.

对类型变量进行独热编码, 共生成48个子变量, 包括性别、学历、收入途径、配偶状态、申请渠道等.

(3)特征衍生

使用原始特征进行训练所得模型的泛化能力往往较差^[13], 且模型很难挖掘特征之间的联系. 故通过传统信用评估经验, 从交易异常程度、用户还款能力两方面构造衍生变量.

其中交易异常程度包括押品价格与贷款比例、渠道商与申请人是否位于同一市区、借款用途与收入途径是否匹配等. 用户还款能力包括近360天内用户逾期次数、借款金额与收入比例等.

(4)特征选择

实验选用Boruta^[14]算法对特征进行选择. Boruta是一种随机森林包装器, 可在不调整参数的情况下对数个特征的重要性进行估计, 筛选出与因变量具有相关性的特征集合. Boruta对每个特征进行计算, 创建出相对应的阴影特征, 根据阴影特征的随机性判断特征的重要程度.

选用XGBoost作为Boruta的学习估计器^[15], 定义80分位数为选择阴影与真实特征的比较阈值, 经过特征工程后得到以下包含4维19个特征的数据集, 如表1所示.

2.2 实现流程

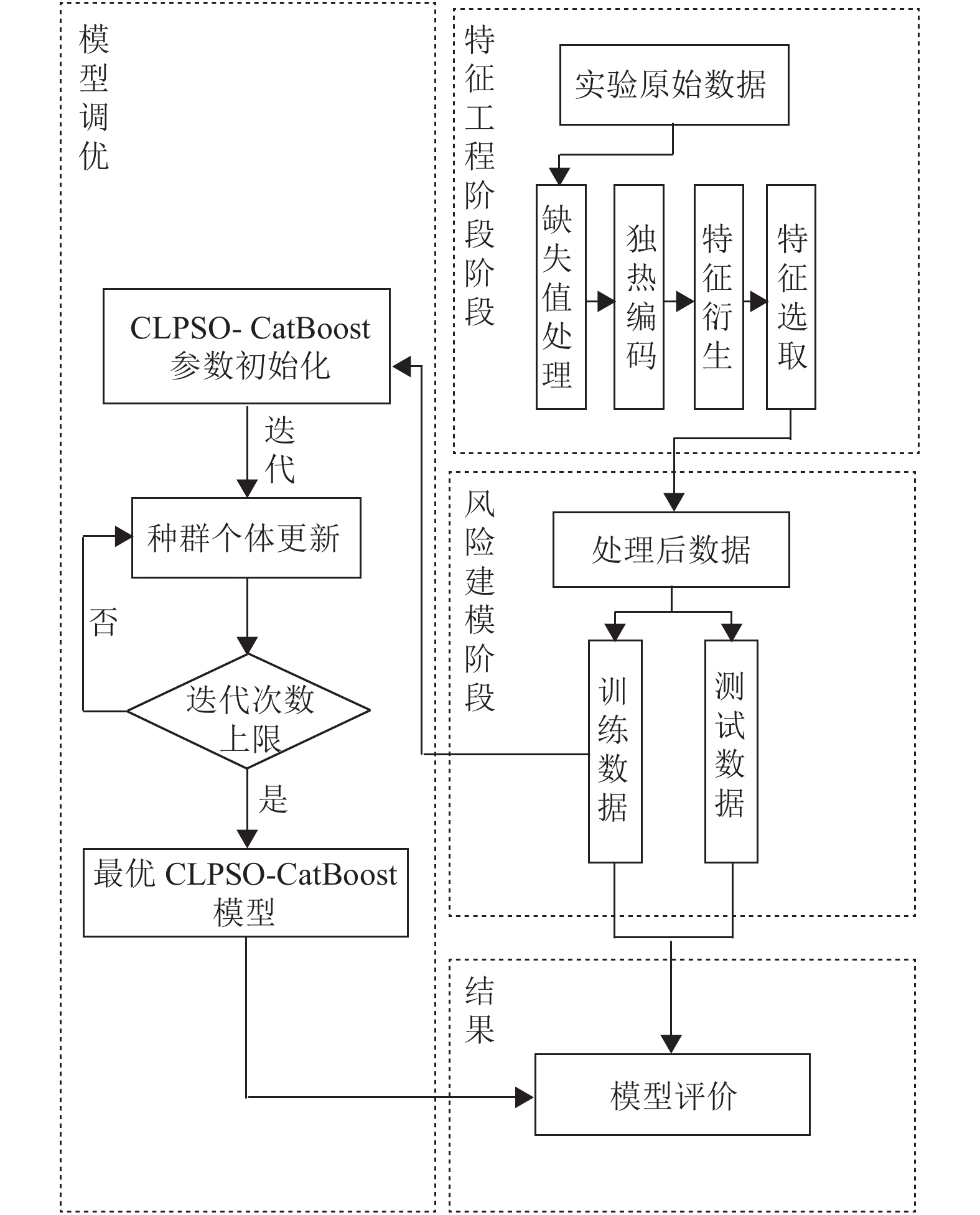
通过特征工程, 实验算法已经可以很好地识别数据进行训练, 但仅采用CatBoost模型进行训练在精度表现上仍有一定提升空间. 因此使用CLPSO算法优化CatBoost模型中的超参数, 包含学习速率、正则子参数及贝叶斯套袋控制强度. 将实验数据按照4:1的比例随机分为训练集与测试集, 并进行试验, 实验步骤如下: ① 数据归一化, 得到可进行实验的数据集D; ② 初始化CLPSO算法参数, 设定粒子总数 $k$ =20, 惯性参数 $\omega $ =20, 维度 $d$ =3, 学习因子 ${c_1}$ =1.5; ③ 使用CatBoost训练模型, 完成后带入测试集, 将交叉熵损失Logloss作为适应度函数^[16]; ④ 粒子群算法迭代, 寻找当适应度函数 $f$ 最小时, 所使用的最优参数向量; ⑤ 将最优参数带入CatBoost模型中训练. 算法流程如图1.

3 实验分析 3.1 评价指标

贷款数据存在数据不平衡的特性, 即违约风险样本数量远小于正常贷款样本数量. 因此当应用分类准确率作为最终评价指标时, 往往会由于违约样本数量过小导致即使误判违约, 准确率也保持在很高的水平. 这样就失去了贷款违约的预测能力, 然而个别贷款违约在日常生活中往往会对金融公司产生很大的代价. 因此将准确率作为评价指标在预测贷款风险的二分类模型中是不合理的. 本文采用AUC值作为评价指标. 将正常贷款样本定义为正样本, 违约样本定义为负样本, 混淆矩阵定义如表2.

根据混淆矩阵, 定义准确率A (accuracy)、精准率P (precision)与召回率R (recall), 定义如下:

$A = {{(TN + TP)} / {(FN + FP + TN + TP)}}$

(5)

$P = {{TP}/ {(FP + TP)}}$

(6)

$R = {{TP} / {(FN + TP)}}$

(7)

根据上述定义, 可以求得ROC曲线, 用以考量针对不平衡样本的预测精度.

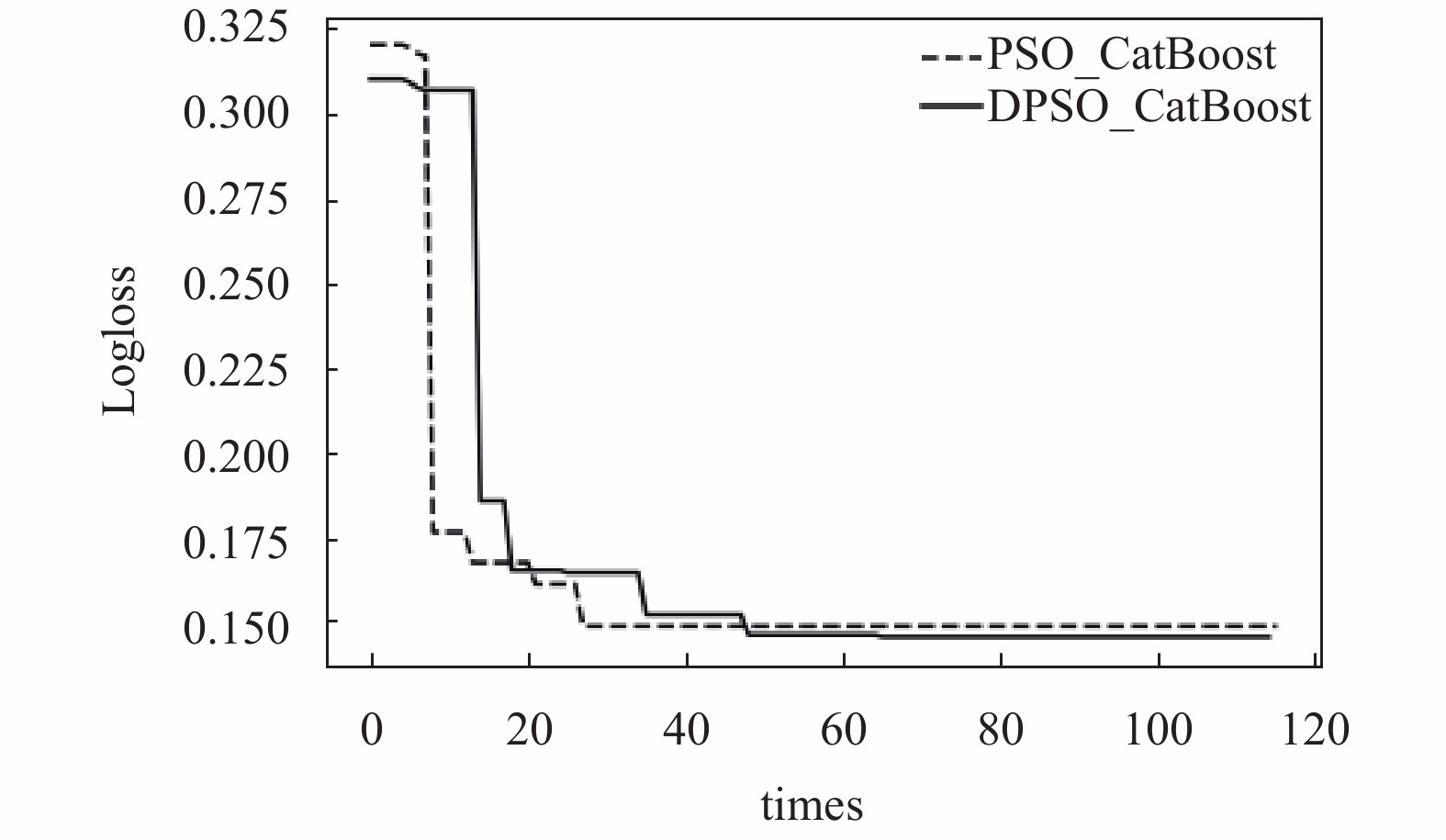
3.2 结果分析

经过综合学习粒子群算法对学习速率、正则子参数及贝叶斯套袋控制强度的调节, 经过120次迭代, 得到最优参数. 将CLPSO-CatBoost与PSO-CatBoost的模型误差率进行对比, 二者迭代过程如图2所示.

PSO与CLPSO算法在优化CatBoost模型时, 二者收敛速度相差不大, 均能在40次内获得良好的优化效果, 但可以发现, PSO算法在随后的迭代中陷入了局部最优, 而CLPSO算法表现出了更好的局部寻优能力. 由此说明, CLPSO算法在优化CatBoost模型时, 能够跳出局部最优, 所得模型对数损失更小. CLPSO-CatBoost模型的准确率90.42%高于并未进行优化的CatBoost模型.

为验证CLPSO-CatBoost模型精确度, 实验引入参数优化前的CatBoost、SVM和XGBoost模型进行训练. 测试集精度如表3所示. 根据结果可知, CLPSO-CatBoost模型在准确率、精准率等方面均有着出色的表现. 相较其他常用模型, CLPSO在精准率上有着些许优势, 而信用贷款风控因其金融属性对精度有着较高的要求.

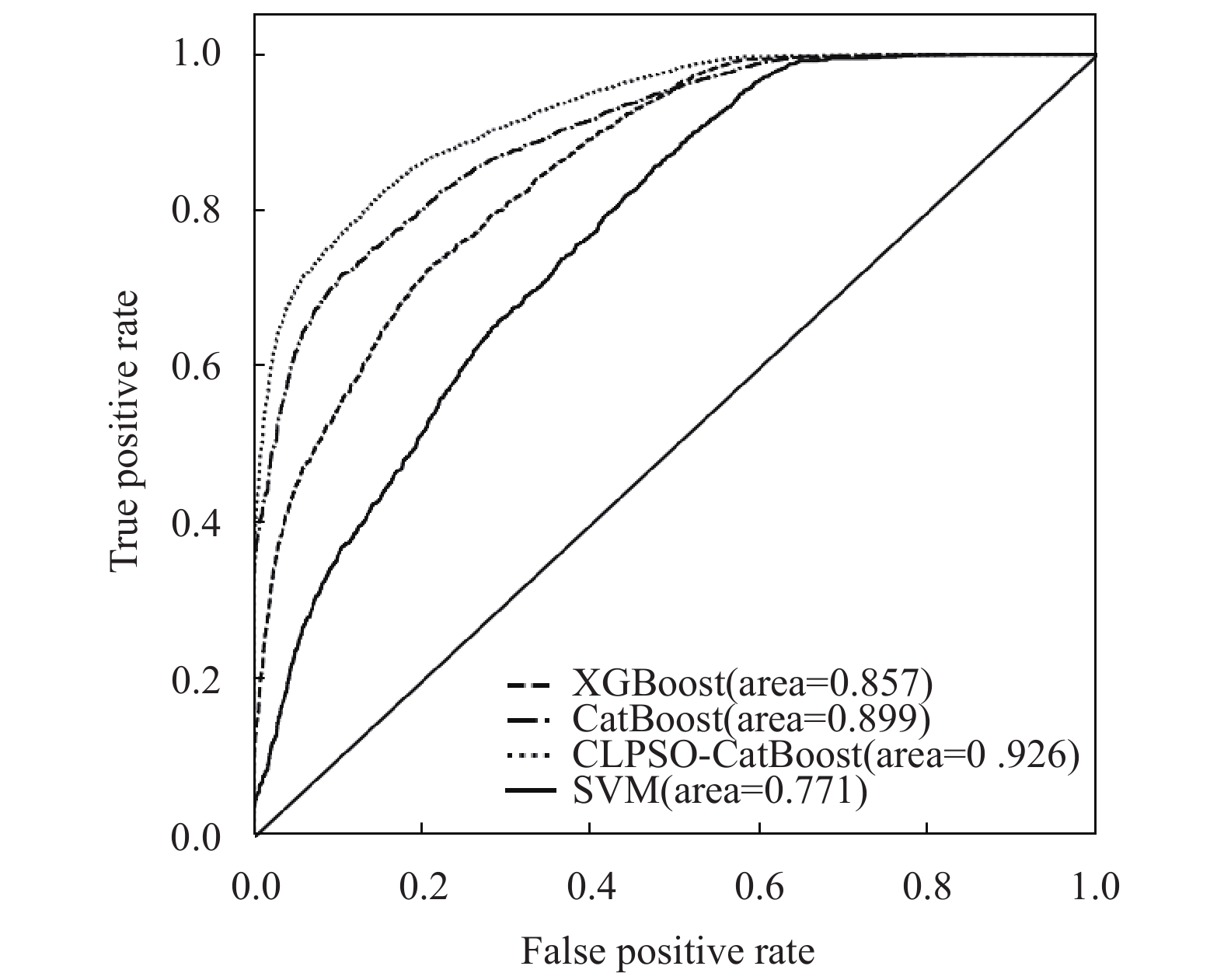
根据实验数据绘制各模型ROC曲线, 所得曲线如图3所示.

由图3可知, CLPSO-CatBoost模型在实验环境下, 有着很好的表现能力.

该模型作为贷款风险预测模型, 实际中贷款申请数量庞大, 模型性能的提升意味着将会更能判别贷款申请是否具有风险, 从而降低金融公司的坏账率. 车贷的借款金额较大且订单数量多, 坏账对金融公司造成的影响较为严重. 因此, 模型性能的提升意味着能够有效的减少坏账损失, 进而维护了金融稳定性, 减少发生信用危机的可能性.

4 结论与展望

本文针对金融机构贷款风险预测问题, 通过国内某金融公司的车辆抵押贷款数据, 从数据采样、特征工程及分类算法方面等方面做了一系列工作, 得出如下结论:

1) 相比于传统分类模型. CLPSO-CatBoost模型在准确率、错误率、召回率和AUC曲线上, 都获得了提升. 面对不平衡数据集, 该模型有着出色的少数类识别率, 具有很高的应用价值.

2) CLPSO作为粒子群算法的一个分支, 通过改进例子学习方式在一定程度上避免了粒子群算法容易陷入局部收敛的问题, 提升了全局学习能力. 在本实验场景下, CLPSO算法表现出优于PSO, CLPSO-CatBoost模型能够有效地提升模型精度.

综上所述, 相比SVM等常用的信用风险评估方法, CLPSO-CatBoost模型能够更有效预测贷款风险.