移动机器人中的路径规划问题被认为是一项复杂的任务. 工业, 医学和农业中机器人的广泛应用鼓励研究人员在路径规划领域开展研究工作. 路径规划者应根据特定标准, 在充满障碍物的环境中, 在机器人的起始位置与目标位置之间找到一条最佳(或接近最佳)的无碰撞路径. 在某些情况下, 机器人所处的环境可能包含危险区域或敏感区域, 在路径规划算法中需要考虑这些危险区域或敏感区域. 除了生成更短的路径, 路径规划算法还需要生成与危险区域和环境中的敏感区域相距安全距离的轨迹. 在路径规划中, 为移动机器人提供自主权的不同元启发式技术的开发是当前探索中最具挑战性的领域之一.
在过去的几十年中, 通过使用一些传统的和启发式方法, 来优化路径规划问题, 如细胞分解(CD), 势场法(APF)[1], 模拟退火, 遗传算法(GA)[2], 粒子群优化(PSO)[3]和神经网络.
通常, PSO非常适合于开发, 但可能导致局部最优问题. 因此, 在某些情况下, PSO无法找到全局最优解. 标准PSO中使用的搜索策略主要基于随机游动, 它不能总是成功地解决优化问题. 为了进一步提高算法的性能, 已将不同策略添加到优化算法中, 例如文献[4]在算法中引入鸡群算法中的母鸡更新方程和小鸡更新方程对搜索停滞的粒子进行扰动, 使粒子跳出较差的搜索区域, 脱离局部最优; 带有变异算子的粒子群优化[5]被用于开发移动机器人路径规划算法. 文献[3]使用随机PSO解决了移动机器人的平滑路径规划问题, 文献[6]使用自适应惯性权重改进的粒子群算法减少粒子群的无效迭代次数, 文献[7]结合差分进化算法中的变异算子来优化粒子群算法的适应度值.
虽然已有文献对PSO进行研究和改进, 但是, PSO在进化过程中会过早收敛, 同时会处理一些复杂的问题, 例如一些基于现实世界的导航优化问题, PSO还取决于用户来调整控制参数例如惯性权重, “社会”和“认知”系数以及速度以实现所需的解决方案. 因此, PSO算法的结构需要进一步改进, 以实现最优解. GA执行交叉和突变操作以重组染色体. 它具有强大的全局搜索功能, 可以在搜索范围内搜索最优问题的最优解或接近最优解, 并且具有优于传统最优技术的性能. 但其主要缺点是, 解决方案更容易陷入局部最小值. 这是由于在搜索空间中仅从单个方向搜索解决方案. 因此, 可以将GA算法改进为从多个方向看作一种搜索方法, 这意味着更容易摆脱局部最小值[8]. 将文献[8]的多重交叉和变异算子, 与IPSO融合, 整合了PSO的开发能力和GA的探索能力, 以实现全局最优.
本文提出了一种混合遗传算法中遗传算子的改进粒子群算法(IPSO-GOP). 首先, 为提高算法搜索能力, 在算法运行的各个阶段利用粒子与全局最优位置的距离对惯性权重进行自适应调整, 采取混沌变量对粒子进行扰动的方法提高收敛速度; 其次, 为了摆脱局部最小值并增加种群的多样性, 引入遗传算法继承的多重交叉和变异两个进化算子协同粒子群优化; 最后, 根据三次样条插值对该混合算法生成的路径进行平滑处理, 得到无碰撞路径最短的几何连续路径.
1 新型混合粒子群优化和遗传算子 1.1 粒子群优化PSO算法是由Kennedy和Eberhard于1995年提出的基于种群的优化问题启发式策略, 与鸟群和鱼类群的行为类似, 在PSO中, 优化问题的候选解决方案集被定义为可能通过参数(搜索)空间定义轨迹的粒子群, 这些空间由它们自己和邻居驱动的最佳表现[9]. PSO中的每个粒子都有一个位置
粒子的速度更新:
| $ \begin{split} v_i^d\left( {t + 1} \right) =& v_i^d\left( t \right) + {c_1}{r_1}\left( {x_{ {\rm pbes}{{\rm {t}}}_i}^d - x_i^d\left( t \right)} \right) \\ & + {c_2}{r_2}\left( {x_{\rm {gbest}}^d - x_i^d\left( t \right)} \right) \\ \end{split} $ | (1) |
粒子的位置更新:
| $\begin{array}{*{20}{c}} {x_i^d\left( {t + 1} \right) = x_i^d\left( t \right) + v_i^d\left( {t + 1} \right)} \end{array}$ | (2) |
式中,
参数控制和自适应一直是粒子群算法研究的热点, 惯性权重w的目的是控制速度, 从而影响收敛性, 几乎所有的粒子群算法都将惯性权重作为速度更新规则的组成部分[10]. 速度更新公式如式(3)所示:
| $ \begin{split} v_i^d\left( {t + 1} \right) =& {w_i}v_i^d\left( t \right) + {c_1}{r_1}\left( {x^d_{{\rm{pbest}}_i}- x_i^d\left( t \right)} \right) \\ & + {c_2}{r_2}\left( {x_{\rm {gbest}}^d - x_i^d\left( t \right)} \right) \\ \end{split} $ | (3) |
每个粒子都用较大的惯性因子值更新其位置和速度, 有利于全局搜索, 而用较小的惯性因子值则有利于局部搜索. 多项研究表明, 对惯性权重进行动态调整可以改善PSO的收敛性, 而线性递减惯性权重已经显示出更好的结果[9]. 因此, 这里采用文献[11]提出的惯性权重的自适应变化, 如式(4)所示. 过去已有实验验证采用组合
| $\begin{array}{*{20}{c}} {{w_i} = {w_{\min}} + \left( {{w_{\max}} - {w_{\min}}} \right)\dfrac{{dis{t_i}}}{{{{max\_ }}dist}}} \end{array}$ | (4) |
| ${dis{t_i} = {{\left( {\displaystyle\sum\limits_{d = 1}^D {x_{\rm {gbest}}^d} - x_i^d} \right)}^{1/2}}}$ | (5) |
| $\begin{array}{*{20}{c}} {max\_dist = \arg \max(dis{t_i})} \end{array}$ | (6) |
式中,
最高的随机运动有益于探索大部分搜索空间. 但是, 最快的收敛速度是开发阶段的主要目标. 局部搜索和梯度下降都可以提高性能, 但是会带来额外的计算成本. 有文献表明, 将混沌理论整合到基于群体的算法中是平衡算法的全局探测和局部开采能力的最小计算成本的方法之一[12]. 由于混沌行为类似于随机性, 但是具有更好的动力学和统计学特性, 与随机搜索相比, 混沌搜索可以更容易地从局部最优解中逃脱. 因此, 将随机参数
| $\begin{split} v_i^d\left( {t + 1} \right) =& {w_i}v_i^d\left( t \right) + {c_1}{r_1}\left( {x^d_{{\rm {pbest}}_i} - x_i^d\left( t \right)} \right) \\ & + {c_2}\xi \left( x^d_{{\rm {gbest}}}{ - x_i^d\left( t \right)} \right) \\ \end{split} $ | (7) |
Singer映射定义如下:
| $\begin{array}{*{20}{c}} {{x_{k + 1}} = \mu \left( {7.86{x_k} - 23.3x_k^2 + 28.75x_k^3 - 13.3x_k^4} \right)} \end{array}$ | (8) |
式中,
当
遗传算法是一种自适应启发式搜索方法, 是进化算法的一种. 其主要思想是根据目标函数构建适应度, 以评估种群中的所有染色体. 经过一定数量的迭代后, 选择适应性最好的染色体作为指定问题的解决方案. 该算法以一组随机选择的染色体作为初始种群开始, 并且两个遗传算子(交叉和突变)创建新的染色体(后代). 选择运算符用于一代又一代地创建总体. 具有更好适应性值的染色体在下一代中具有更高的概率被选择. 在下文中, 主要介绍其中两个算子, 多重交叉和突变.
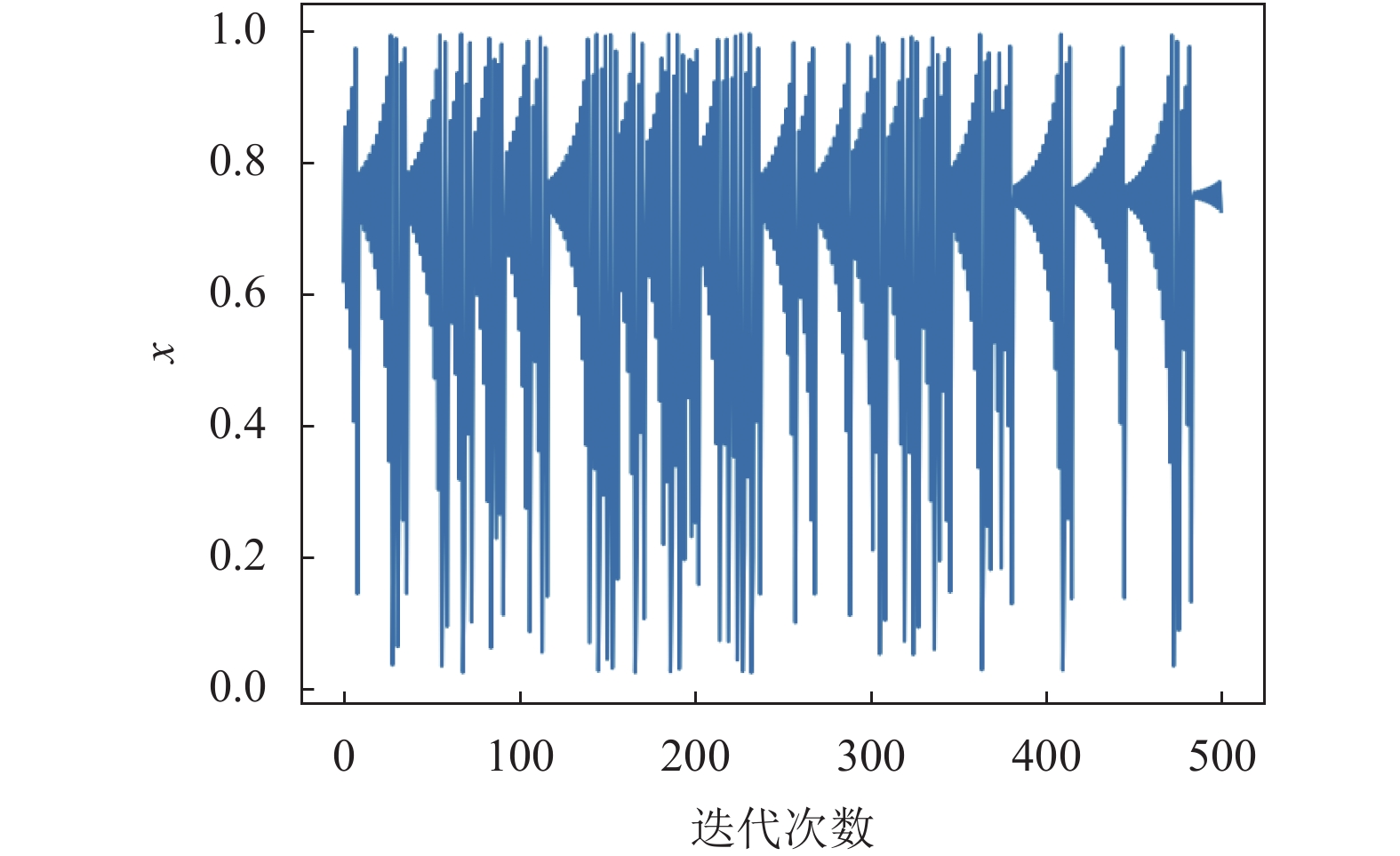
|
图 1 Singer 映射 |
多重交叉: 该运算符是基于文献[8]中改进遗传算法的交叉公式即多重交叉. 多重交叉使用的3个染色体(
| $\begin{array}{*{20}{c}} {\theta _i' = {\theta _i} + {\rm {rand}}\left( {2{\theta _1} - {\theta _2} - {\theta _3}} \right)} \end{array}$ | (9) |
式中, rand是0到1之间的随机值
粒子的更新速度计算公式如下:
| $\begin{array}{*{20}{c}} {v_i^d\left( {t + 1} \right) = {\rm {rand}}\left( {2x_{\rm {gbest}}^d - x_i^d\left( t \right) - x_{{\rm {pbest}}_i}^d} \right)} \end{array}$ | (10) |
突变: 变异是一个过程, 其中包括通过应用某种随机变化对染色体的位进行小的改变. 变异算子在GA中起至关重要的作用, 可以有效维持种群的多样性, 避免算法陷入局部最小值.
1.4 IPSO-GOP算法由于依赖于外部参数(例如惯性权重和加速度参数), 传统的PSO算法难以生成最优解, 并且收敛速度较慢. 因此, PSO算法的效率相对较差. 在大多数情况下, 当大多数粒子在连续阶段中不改变其在群体中的位置时, 会聚为时过早, 产生的最优解较少, 因此无法找到全局最优解. 由于在PSO算法中遇到了上述问题, 因此已采取了措施来改善PSO的性能, 即通过进化算子调节IPSO的速度多样化搜索空间以消除过早收敛.
在这种杂交中, 使用两个进化算子更新了IPSO的粒子的位置. 在所有粒子都构建完成后, 根据突变概率
改进后算法流程如算法1.
算法1. IPSO-GOP算法
1) 初始化种群大小, 搜索空间, 迭代次数, 粒子的初始位置和速度
2) 根据适应度函数评价每个粒子的适应度
3) 根据突变概率更新粒子的位置
4) 更新每个粒子经历过的最好位置pbest和全局所经历最好位置gbest, 并且根据式(4)计算w
5)判断
6)根据式(7)更新粒子的速度
7)根据式(10)更新粒子的速度
8)使用式(2)对粒子位置进行更新
9)计算位置更新后各粒子的适应度值并更新个体最优适应度值以及全局最优适应度值
10)判断是否满足停止条件, 若是, 输出最优适应度值, 否则转至步骤 2)
2 目标函数与三次样条插值 2.1 目标函数在给出环境, 设初始位置和目标位置后, 将所提出的IPSO-GOP算法应用于计算无碰撞轨迹.
路径长度影响机器人的运输时间, 为更快完成任务, 通过形成第一个目标函数
| $\begin{array}{*{20}{c}} {{f_1} = d\left( {{p_j}\left( t \right),{p_j}\left( N \right)} \right)} \end{array}$ | (11) |
式中,
最短距离长度为起始点
| $\begin{array}{*{20}{c}} {{f_1} = \displaystyle\mathop \sum \limits_{t = 1}^{N - 1} \sqrt {{{\left( {{x_{{p_j}\left( {t + 1} \right)}} - {x_{{p_j}\left( t \right)}}} \right)}^2} + {{\left( {{y_{{p_j}\left( {t + 1} \right)}} - {y_{{p_j}\left( t \right)}}} \right)}^2}} } \end{array}$ | (12) |
第2个目标函数为惩罚函数, 若路径上有一路径线段与障碍物碰撞, 则惩罚函数乘以一个惩罚因子
| $\begin{array}{*{20}{c}} {{f_2} = \displaystyle\mathop \sum \limits_{i = 1}^{{M_{\max}}} \delta {\alpha _i}} \end{array}$ | (13) |
式中,
总目标(适应度)函数如下:
| $\begin{array}{*{20}{c}} {fit = {f_1} + {f_2}} \end{array}$ | (14) |
本文路径规划地图采用栅格地图表示, 因此会在转弯处产生尖峰. 为了让移动机器人减少实际机器人轮子的轴磨损和能耗, 应保证路径的平滑性, 尽量保证平滑处理后的路径与实际路线相同.
由于拉格朗日插值法因龙格现象在分段曲线边缘处的拟合误差影响路径的平滑度. 三次样条曲线线性光滑,具有连续的二阶导数;能够保证拟合曲线通过所有的规划的路径点.
三次样条插值具有一阶和二阶导数的收敛性. 当三次函数的最高项系数为0时, 三次样条插值曲线仍为曲线, 插值效果应更好. 另外, 三次样条插值与高阶插值相比, 具有计算简单, 稳定性好的优点. 由于三次样条插值已得到广泛应用[14], 并在路径平滑方面的应用效果很好[15,16], 因此本文使用三次样条插值形成平滑路径.
取区间
在每个小区间
| $\begin{array}{*{20}{c}} {{S_i}\left( x \right) = {a_i} + {b_i}\left( {x - {x_i}} \right) + {c_i}{{\left( {x - {x_i}} \right)}^2} + {d_i}{{\left( {x - {x_i}} \right)}^3}} \end{array}$ | (15) |
| $\begin{array}{*{20}{c}} {S\left( {{x_0}} \right) = {y_0}, \cdots ,S\left( {{x_{n + 1}}} \right) = {y_{n + 1}}} \end{array}$ | (16) |
| $\begin{array}{*{20}{c}} {{S_ - } = {S_ + }\left( {{x_i}} \right),i = 1,2, \cdots ,n} \end{array}$ | (17) |
| $\begin{array}{*{20}{c}} {S_ - ^{\rm{'}} = S_ + ^{\rm{'}}\left( {{x_i}} \right),i = 1,2, \cdots ,n} \end{array}$ | (18) |
| $ \begin{array}{*{20}{c}} {S_ - ^{{\rm{''}}} = S_ + ^{{\rm{''}}}\left( {{x_i}} \right),i = 1,2, \cdots ,n} \end{array} $ | (19) |
在本文中, 三次样条函数用于在起点, 控制点和目标点的路径上进行插值, 可以将移动机器人的路径绘制为一系列连接路径点的线段, 从而获得了通过连接所有插值点而形成的完整路径.
3 实验分析为了验证本文提出算法的有效性, 对算法寻优性能进行测试与对比. 并在仿真环境下对机器人的路径规划问题进行了研究, 以起点S(0,0), 终点G(20, 20)在不同障碍物环境进行路径规划, 并利用三次样条插值对路径进行拟和修正. 最后, 针对相同环境下与不同算法的每次迭的最优适应度值进行对比. 计算环境均为操作系统: Window10、CPU: Intel Core i5、编程语言: Python 3.7.
3.1 函数优化为了评估本文所提出算法的性能, 本文选取了5个标准测试函数, 由于其大多数全局最小值为0, 复杂性更高, 所以移动和偏差这些测试函数. 测试函数如表1所示.
| 表 1 标准测试函数 |
初始参数为: 种群数: 30, 迭代次数: 500. 其中, PSO加速常量
| 表 2 函数优化结果 |
3.2 路径生成与修正
建模环境为: 设计具有不同障碍物数量的20×20网格工作区, 如图2所示, 图中
在仿真实验中, 不同障碍物数量环境中的参数设置如表3所示.

|
图 2 全局路径规划仿真实验图 |
| 表 3 算法的相关参数 |
图3为本文所提出的算法在多障碍物环境下规划出的路径和采用三次样条插值平滑后的路径. 由于可行路径必须经过附近障碍物形成的一些狭窄空间, 所以最优解很可能是具有次优目标的函数值的不可行路径. 本文所提算法很好完成了在多障碍物环境下规划平滑路径的任务. 如图3所示, 其中红色实线表示用于移动机器人运动的更平滑的路径. 每次迭代中最佳粒子的最佳的目标函数值如图4所示, 表明本文所提出的算法针对该问题能够快速收敛.
3.3 与其他路径规划算法比较对比算法选用粒子群优化(PSO)、混合遗传算法和粒子群优化(GA-PSO)[17]两种相关算法, 所有算法设置的参数(惩罚因子除外)与表2相同, 为了让搜索结果更明显, 开始迭代适应度值更小, 这里设置惩罚因子

|
图 3 多障碍物环境下PSO-GOP算法路径规划结果 |

|
图 4 复杂环境下IPSO-GOP算法收敛曲线 |

|
图 5 IPSO-GOP与GA-PSO路径图 |
为了保证结果的可靠性, 对比算法和本文算法分别进行了10次独立的实验, 路径规划仿真10次结果如图7所示. 10次实验结果对比显示, IPSO-GOP算法更稳定, 平均最佳适应度值最好.
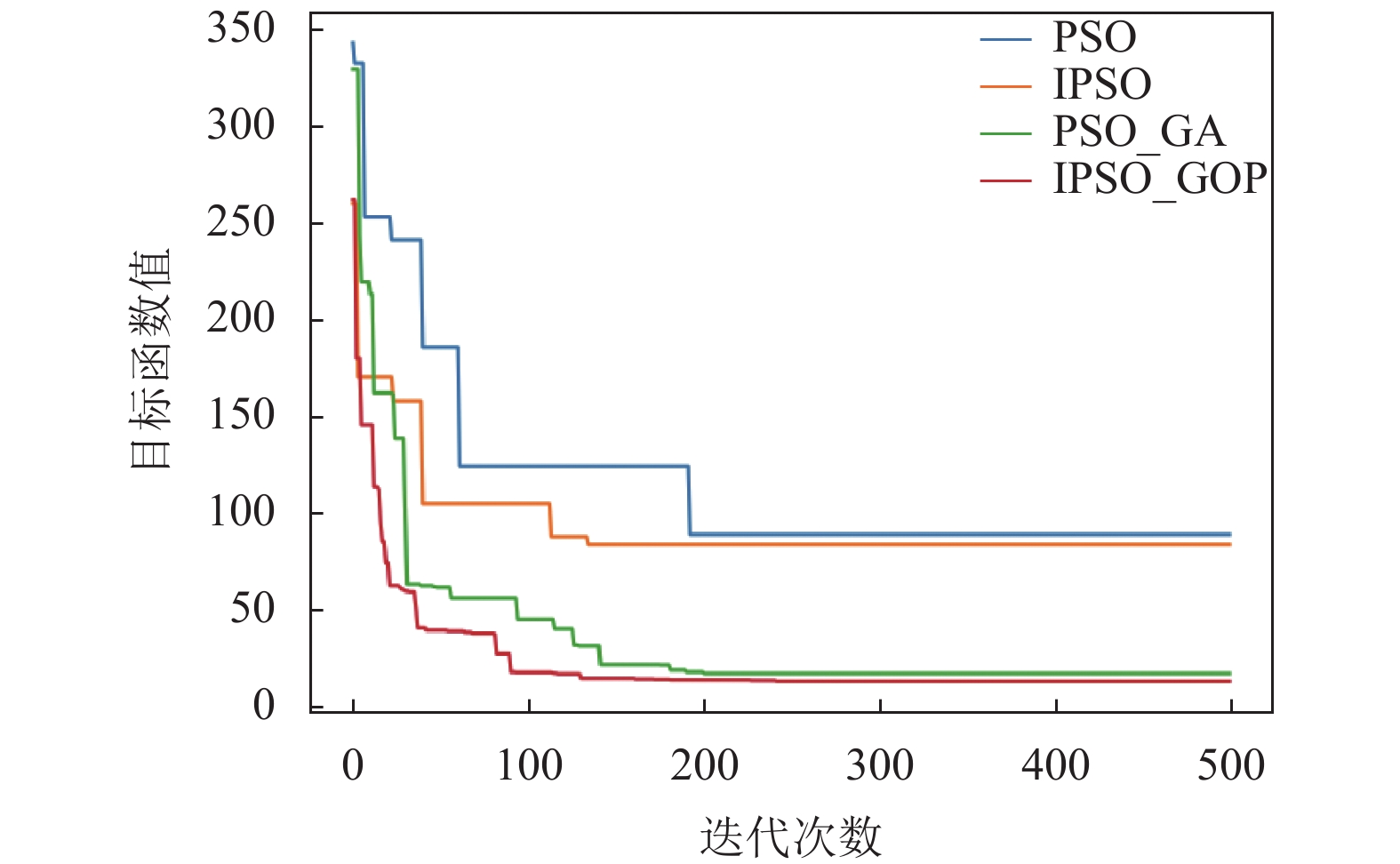
|
图 6 目标函数值与迭代次数的关系 |

|
图 7 10次实验对比结果 |
4 结束语
本文提出了一种IPSO-GOP混合算法, 以寻找在充满障碍物环境中移动机器人从预定起点到终点的无碰撞最短光滑路径. 所提出的算法使用遗传算法中的遗传算子(多重交叉和突变)优化IPSO, 将IPSO的社会本质与GOP的多样性相结合, 减少了局部最优的发生, 同时满足了收敛速度. 实验结果表明, IPSO-GOP算法性能优于其他现有的启发式算法. 仿真实验中, 与已有的元启发式算法(如PSO)和混合算法(如GA-PSO)比较, 可以得出, IPSO-GOP算法优于障碍物环境中路径规划的其他算法.
| [1] |
Ge SS, Cui YJ. Dynamic motion planning for mobile robots using potential field method. Autonomous Robots, 2002, 13(3): 207-222. DOI:10.1023/A:1020564024509 |
| [2] |
Elhoseny M, Tharwat A, Hassanien AE, et al. Bezier curve based path planning in a dynamic field using modified genetic algorithm. Journal of Computational Science, 2018, 25: 339-350. DOI:10.1016/j.jocs.2017.08.004 |
| [3] |
Chen X, Li YM. Smooth path planning of a mobile robot using stochastic particle swarm optimization. Proceedings of 2006 International Conference on Mechatronics and Automation. Luoyang, China. 2006. 1722–1727.
|
| [4] |
贾会群, 魏仲慧, 何昕, 等. 基于改进粒子群算法的路径规划. 农业机械学报, 2018, 49(12): 371-377. DOI:10.6041/j.issn.1000-1298.2018.12.044 |
| [5] |
Qin YQ, Sun DB, Li N, et al. Path planning for mobile robot using the particle swarm optimization with mutation operator. Proceedings of 2004 International Conference on Machine Learning and Cybernetics. Shanghai, China. 2004. 2473–2478.
|
| [6] |
敖永才, 师奕兵, 张伟, 等. 自适应惯性权重的改进粒子群算法. 电子科技大学学报, 2014, 43(6): 874-880. DOI:10.3969/j.issn.1001-0548.2014.06.014 |
| [7] |
吴静, 罗杨. 动态调整惯性权重的粒子群算法优化. 计算机系统应用, 2019, 28(12): 184-188. DOI:10.15888/j.cnki.csa.007162 |
| [8] |
Chang WD. A multi-crossover genetic approach to multivariable PID controllers tuning. Expert Systems With Applications, 2007, 33(3): 620-626. DOI:10.1016/j.eswa.2006.06.003 |
| [9] |
Marini F, Walczak B. Particle swarm optimization (PSO). A tutorial. Chemometrics and Intelligent Laboratory Systems, 2015, 149: 153-165. DOI:10.1016/j.chemolab.2015.08.020 |
| [10] |
Burman R, Chakrabarti S, Das S. Democracy-inspired particle swarm optimizer with the concept of peer groups. Soft Computer, 2017, 21(12): 3267-3286. |
| [11] |
Zhan ZH, Zhang J, Li Y, et al. Adaptive particle swarm optimization. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2009, 39(6): 1362-1381. DOI:10.1109/TSMCB.2009.2015956 |
| [12] |
Gandomi AH, Yun GJ, Yang XS, et al. Chaos-enhanced accelerated particle swarm optimization. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(2): 327-340. DOI:10.1016/j.cnsns.2012.07.017 |
| [13] |
Tharwat A, Elhoseny M, Hassanien AE, et al. Intelligent Bézier curve-based path planning model using Chaotic particle swarm optimization algorithm. Cluster Computing, 2019, 22(2): 4745-4766. |
| [14] |
范云锋, 刘博, 郑益凯. 一种基于三次样条曲线的目标航迹拟合与插值方法研究. 数字技术与应用, 2019, 37(3): 128-129. |
| [15] |
Lian JF, Yu WT, Xiao K, et al. Cubic spline interpolation-based robot path planning using a chaotic adaptive particle swarm optimization algorithm. Mathematical Problems in Engineering, 2020, 1849240. |
| [16] |
强宁, 高洁, 康凤举. 基于PSO和三次样条插值的多机器人全局路径规划. 系统仿真学报, 2017, 29(7): 1397-1404. |
| [17] |
Huang HC, Tsai CC. Global path planning for autonomous robot navigation using hybrid metaheuristic GA-PSO algorithm. Proceedings of 2011 SICE Annual Conference. Tokyo, Japan. 2011. 1338–1343.
|
 2021, Vol. 30
2021, Vol. 30


