2. 国网电力科学研究院有限公司, 南京 211106
2. State Grid Electric Power Research Institute Co. Ltd., Nanjing 211106, China
2020年4月21日, 国家发改委首次明确“新基建”范围, 区块链被正式纳入其中. 区块链是时下的热点和焦点, 作为新一代互联网的底层系统, 区块链可以融合其他新一代信息技术, 加速第三产业转型和创新. 随着能源互联网的发展以及分布式能源渗透率的提高, 基于区块链技术的对等(Peer to Peer, P2P)能源交易也受到了极大关注[1]. 同时, 配电网也从原先只能向负荷提供电能的单相潮流转变为既能提供电能又能接受电能的双向潮流[2].
文献[3]系统地回顾了区块链在电力和能源领域相关的应用、挑战和机遇. 文献[4]在基于能源互联网的条件下, 建立了具有储能设施的分布式光伏电站微电网区块链交易模型, 分析了区块链在电能交易市场中的应用. 文献[5]提出了区块链应用于能源互联网的具体架构, 通过仿真和建模定性和定量地分析了区块链交易的影响因素, 并且建立了数学模型, 实现进行定量, 为电力交易区块链的具体设计提供了参考. 文献[6]通过对典型低压配电网进行详细建模和仿真, 提出了一种能源交易机制, 使得电力系统更加去中心化运营. 国内外的几个项目也证明了在低压配电网或微电网上使用区块链实现对等能源交易的概念[7-9].
上述文献主要是对区块链在能源交易市场上的应用以及在去中心化电力交易方面有重要的研究. 然而, 到目前为止, 这一领域的大部分工作都集中在微电网的能源交易机制, 或在多个电网之间的能源共享. 关于分析基于区块链的地方电能交易对配电网基础设施可能产生的影响方面, 则存在一个研究缺口. 由于政策环境、投资、落地标准等因素影响, 中国目前落地的电力交易区块链应用极少, 并且也面临着区块链吞吐量增大问题以及安全性防护问题等问题和挑战. 本文通过提出一种基于区块链技术的P2P电能交易平台与配电网的协同仿真框架来研究其对配电系统的控制、运行和规划可能产生的影响. 从而为区块链技术在电力交易中的落地应用提供技术参考和理论依据. 本文采用基于区块链的分布式双边拍卖交易平台促进用户之间的P2P电能交易, 并通过OpenDSS (Open Distributed System Simulator)对某一社区用户微电网进行了两个场景的建模和仿真. 通过算例仿真结果研究分析了P2P电能交易平台对当地配电网的影响.
1 协同仿真方法概述目前为了使P2P能源交易模式得到更大规模的应用, 需要对其进行建模来研究其对配电网的性能和可靠性的潜在影响. 本文选择OpenDSS仿真工具[10]. OpenDSS是一个用于对三相低压网络进行详细建模的开放源代码工具, 并且还能够通过内置的组件对象模型与Python或Matlab软件包进行交互. 通过使用Python或Matlab来管理数据输入/输出以及使配电网进行仿真运行. 图1是本文所提出的配电网与P2P电能交易平台协同仿真方法示意图.
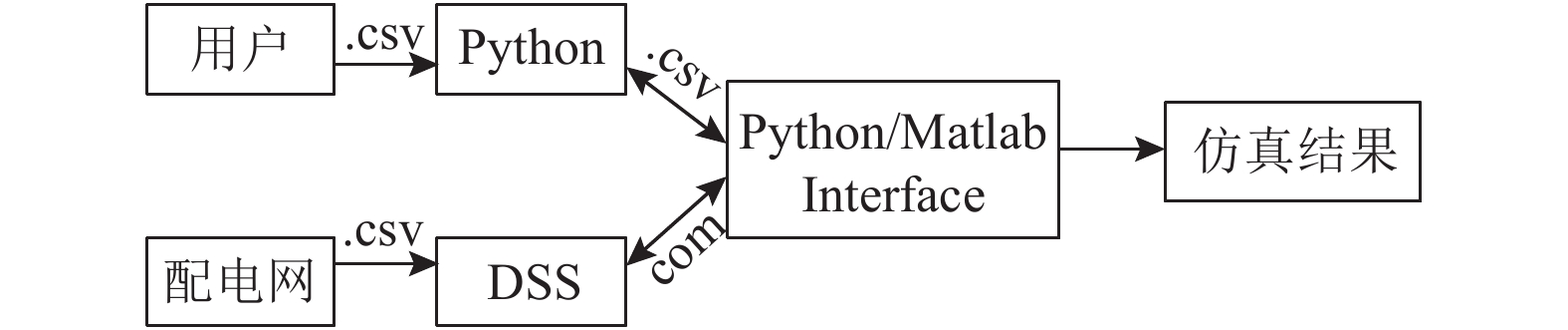
|
图 1 配电网与P2P电能交易平台协同仿真方法示意图 |
输入包括用户数据和配电网数据. 其中用户数据包括用户的日常需求负荷以及PV和EV需求. 配电网主要是网络的节点和支路数据. 配电网数据为OpenDSS提供配电网物理结构的必要信息, 包括网络布局以及变压器、稳压器等网络控制元件的特性参数. 在OpenDSS仿真过程中, 使用逗号分隔值(.csv)文件在每个元素之间交换数据. 最后, 通过Python或Matlab来管理数据输入/输出, 并提供仿真输出的后处理和可视化操作.
在本文中, Matlab用于提供Python与OpenDSS之间的接口, 该接口能够快速解决复杂的三相不平衡网络问题. 图1所示的协同仿真方法的优越性在于OpenDSS中的网络模型可以替换为另一个配电网, 而无需重新编写用于电能交易的Python代码. 同时, 也可以在Python中实现替代的本地能源交易机制, 而不需要在OpenDSS中进行更改. 并且, 考虑到相关的约束条件, 本文所提出的协同仿真方法可以对低压配电网络中的P2P能源交易进行全面的数值仿真, 包括电压、网络支路负载限制、电能质量要求和故障等级等.
2 P2P电能交易平台 2.1 P2P电能交易平台现状P2P电能交易是一种高效协调电力系统中分布式能源的手段. 随着分布式能源渗透率的不断提高, 电能市场的交易模式也迎来了新的机遇和挑战. 通常, 分时电价被用作有效地激励需求响应的一种手段. 但其也面临着问题, 比如如果所有用户都利用相同的低电价时段, 则有可能减小负荷不均性系数并创造新的需求高峰. 所以, 就长远来看, P2P电能交易模式更能有效提高配电网的利用率. 首先, P2P电能交易平台为分布式能源节点提供了一个网络环境, 而不是传统的分层网格结构, 这有利于配电网与其他软件或系统环境进行交互. 但是, 此类项目通常会受到地区以及相关市场法规的限制.
相关研究中, 目标基本都是探索如何进行大规模P2P能源交易的解决方案. P2P电能交易的预期收益主要包括更好地利用电网资源, 以及由于更短的传输距离而减少的能源损失. 在配电网级别上, P2P电能交易平台可以在有足够的分布式能源的情况下实现本地能源平衡.
2.2 分布式双边拍卖机制本文提出了基于P2P电能交易平台的分布式双边拍卖机制. 在分布式双边拍卖机制中, 买卖双方向拍卖商提交他们的保留价格和购买或出售的能源量. 买方的保留价格是它将为能源支付的最高价格, 而卖方的保留价格是卖方将其能源出售的最低价格. 拍卖商决定能源交易的价格和交易的买卖双方的子集.
相较于集中式拍卖的中心化、不安全性以及交易距离限制等缺点, 本文提出的基于区块链的分布式双边拍卖机制则能有效缓解这些问题. 首先, 加密和分布式共识协议保证了区块链中存储的交易记录的安全性. 同时在分布式双边拍卖机制中, 任何参与者都可以作为拍卖商, 区块链机制确保每一个参与者作为拍卖商都是合法的.
在P2P电能交易平台中, 每个用户不仅仅是消费者, 同时也是生产者. 本地能源包括可控制的电能需求, 比如电动汽车充电器、电动热泵、智能电器、现场发电设备以及电池存储设备等. 图2给出了基于P2P电能交易平台的分布式双边拍卖机制示意图.
如图2所示, 任一用户都可以通过交易将其电能供需情况通知到其他用户. 同时, 如果一名用户从其他用户处收到多个供求交易请求, 那么此用户就可以作为拍卖商. 如果一名用户不能解决此双边拍卖交易, 那么它会将未完成的交易信息传递给另一个用户. 相反, 如果成功进行了双边拍卖交易, 则向交易的另一方发送交易成功的信号.
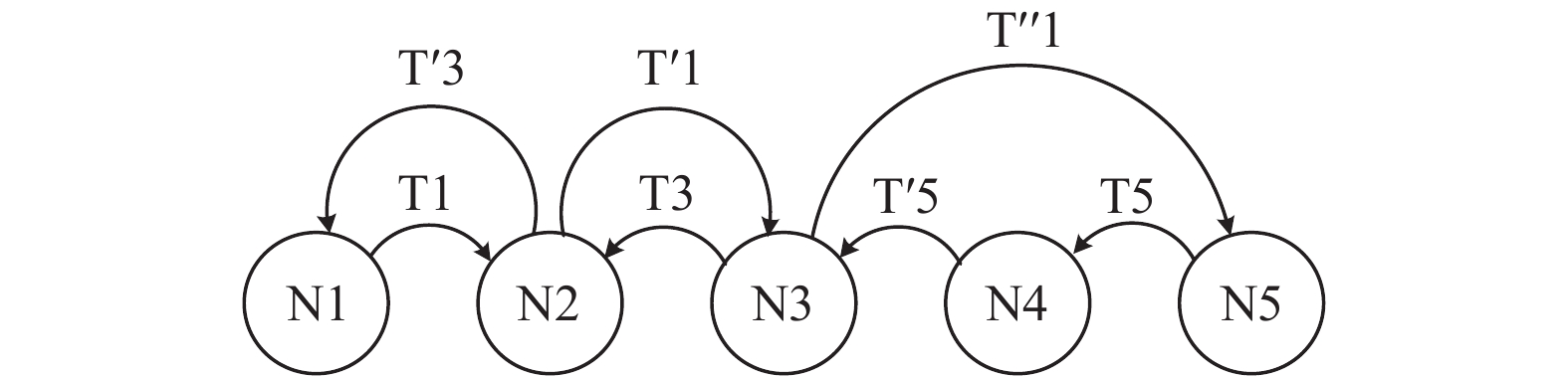
|
图 2 基于P2P电能交易平台的分布式双边拍卖机制示意图 |
在交易过程中, 能源过剩或不足的信息会被编码为区块链交易, 用户向外部发送能源过剩或不足的交易请求. 例如, N1将交易T1发送到N2表示它有多余的能源, 而N3将交易T3发送到N2表示它的能源不足. 用户将根据实际需求来创建合适的交易. 例如, N2发现N3和N5需要购买能源, 而N1在出售多余的能源. 所以, N2就会创建交易T′1, T′′1和T′3. 如果用户无法完成双边拍卖, 那么它将把未完成的交易转给其他用户. 例如, N4通过交易T5接收到N5的能源不足信息, 但无法进行双边拍卖. 因此, N4将此信息传递给N3, 即创建交易T′5, 由N3来完成双边拍卖交易.
双边拍卖的结果仅表明用户理论上的能源需求情况. 但是, 实际的能源需求情况可能不同, 这种情况将被记录为需求字段为0的交易. 因此, 本文通过创建智能合约来解决这一问题.
2.3 智能合约基于每次双边拍卖的结果, 用户之间可以形成一个智能合约. 例如, 在时间
该智能合约将由
最后, 每个用户根据实际情况以及历史能源供应需求信息计算自己的能源需求. 要注意的是, 如果用户发出的能源需求信息和实际能源消耗之间故意不匹配的话, 则会影响交易过程. 区块链将会保存信息记录, 任何此类恶意行为都可以被识别. 图3为智能合约执行流程图.
(1)假定以5分钟作为一个固定时间间隔执行如图3所示步骤.
(2)在此智能合约模型中, 本文假设政府或监管机构将提供足够的资金来创建这些智能合约.
(3)在买卖双方账号都被判定为有效账号的情况下买卖双方将通过Hash算法(SHA256)向智能合约发送其投标的Hash值.
(4)在一段固定的时间间隔之后, 比如在5分钟间隔中的1分钟之后, 智能合约将执行文献[11]算法来确定拍卖的获胜者.
(5)用户的智能电表的数据将被输入智能合约, 以验证参与者之间的实际能源传输.
(6)最后, 在交易达成共识的基础上, 将进行能源传输以及资金转移, 交易数据会被存储到区块链上, 交易成功.

|
图 3 智能合约执行流程图 |
要注意的是, 以上智能合约是在区块链交易结算与电网运营之间进行协同作用的假设中执行的. 本文提出的区块链模拟器可以预测交易确认时间. 该方法的设计使得预期交易确认时间和市场结算时间通常小于在分布式网络仿真中使用的时间步长. 这确保了区块链能源交易的执行时间与配电网模拟之间的协同作用.
本文所描述的分布式双边拍卖可以作为能源交易模型的一个例子, 也可以使用任何其他交易模型. 其特点之一就是具有收敛性, 即拍卖是在有限条件下完成, 比如用户签订智能合同的次数是有限的, 如图4所示.
2.4 区块链网络仿真区块链技术在拓扑形式以及运营方式等方面与新一轮电改下的电力交易市场建设相契合. 本文将区块链技术的特性与P2P电力交易平台相结合, 运用区块链技术, 对电能交易过程中各节点进行身份脱敏处理, 匿名交易和数据无缓存特征为电能交易和双向互动提供重要保障. 区块链仿真是基于网络节点模拟器ns-3实现的. 区块链节点拓扑网络将由仿真程序随机生成. 本文使用区块链分叉数和区块链吞吐量来表示区块链的仿真特性. 交易完成和阻塞所需的时间取决于区块链网络中的通信延迟时间. 同时, 区块链节点数也会影响区块链的性能. 因为区块链节点越多, 节点之间传播数据所需要的时间就越多. 同时, 在区块链网络规模越大, 创建的交易数量也会越多.
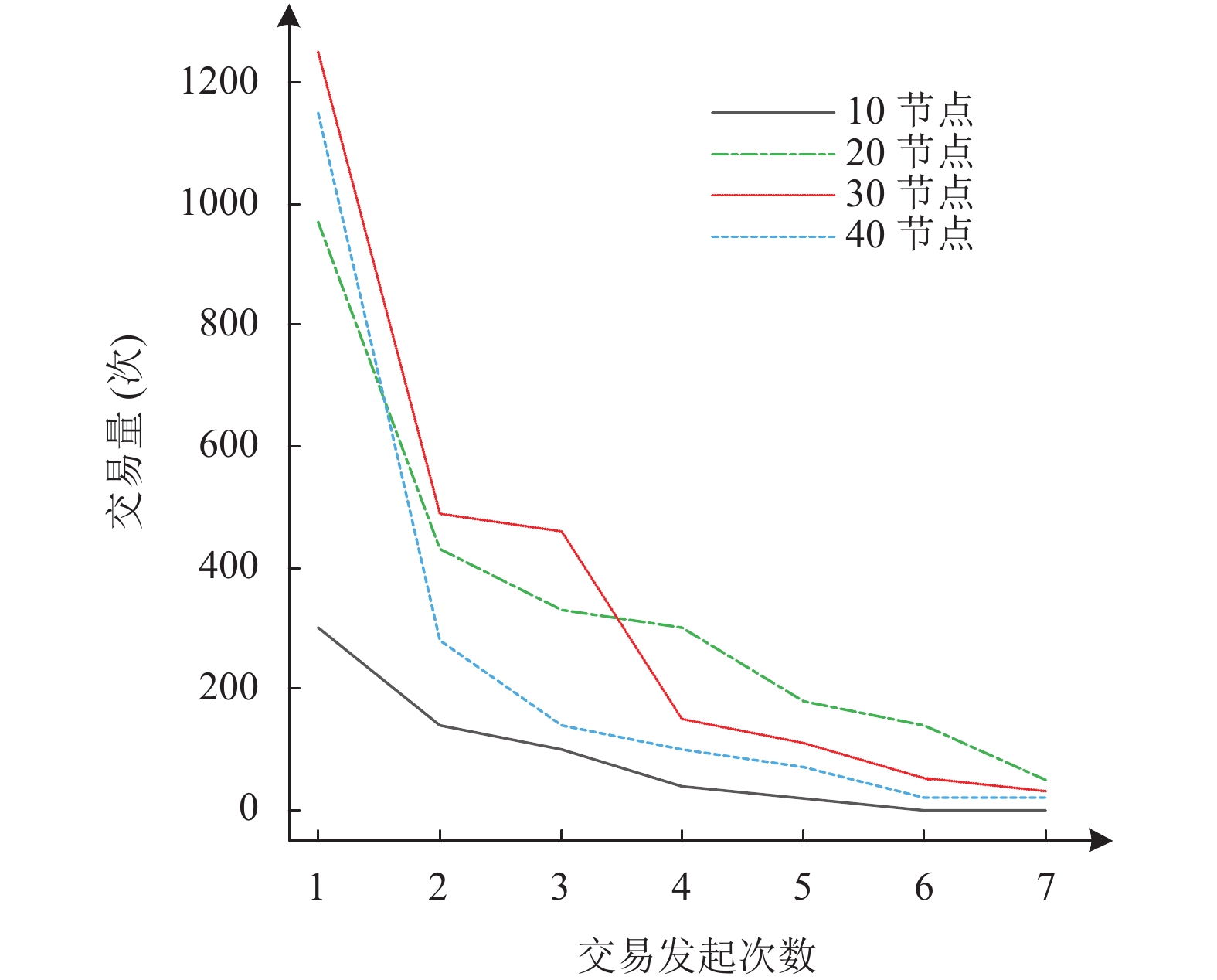
|
图 4 分布式双边拍卖的收敛性 |
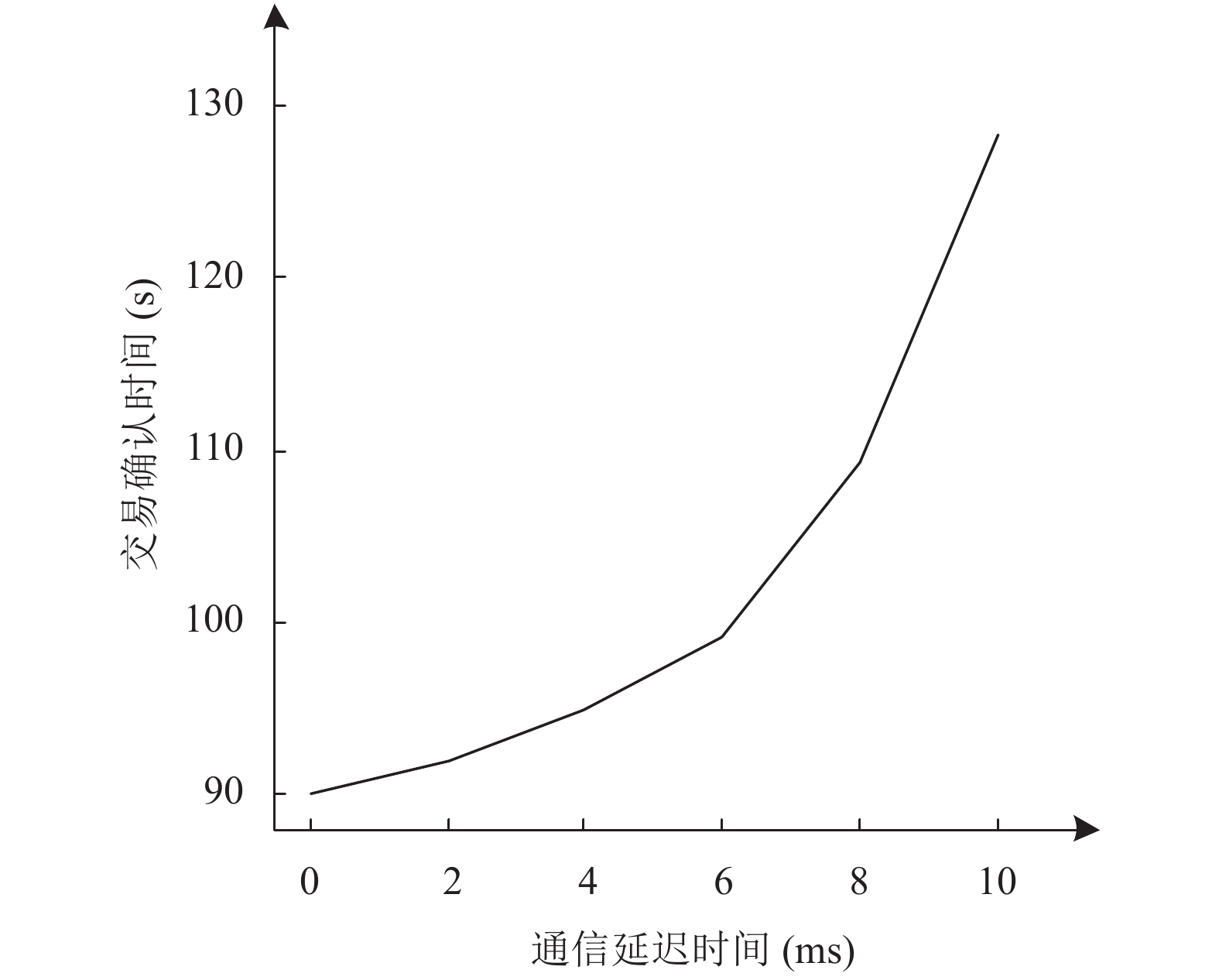
区块链分叉是指区块链分裂成多个区块链的现象. 比如在区块链网络中, 可能会出现多个矿工同时创建一个新的区块的情况. 这时, 部分区块链将接收一个新的区块, 并驳回另一个区块. 区块链的分叉问题在于使用分叉的区块链可能会产生双重支出. 因此, 共识机制可以用来有效解决区块链分叉问题. 例如, 在基于工作量证明机制中, 分叉区块链的最长分支被认为是有效的区块链, 而分叉区块链的较短分支将被驳回. 交易确认时间可以计算为从创建区块链到将交易记录到新的区块所需的时间, 它将直接影响区块链的吞吐量. 本文将通过仿真研究通信延迟时间与区块链分叉数以及交易确认时间的关系. 本文模拟了一个拥有200个节点和40个矿工的区块链网络. 图5是区块链分叉数与通信延迟时间之间的关系示意图.
从图5中可以看出, 随着通信延迟时间的增加, 区块链的分叉数也随之增加. 该结果也支持了所使用的区块链仿真程序的有效性. 因为随着通信延迟时间的增加, 多个矿工同时创建新区块的概率也会增加. 在创建新区块之后, 矿工将其发布到网络, 而其他的矿工在接收到一个新区块后重新开始其挖掘过程. 由于通信延迟时间较长, 信息到达所有矿工的时间将延长, 并且矿工重启采矿过程的可能性较小. 图6是交易确认时间与通信延迟时间关系示意图.
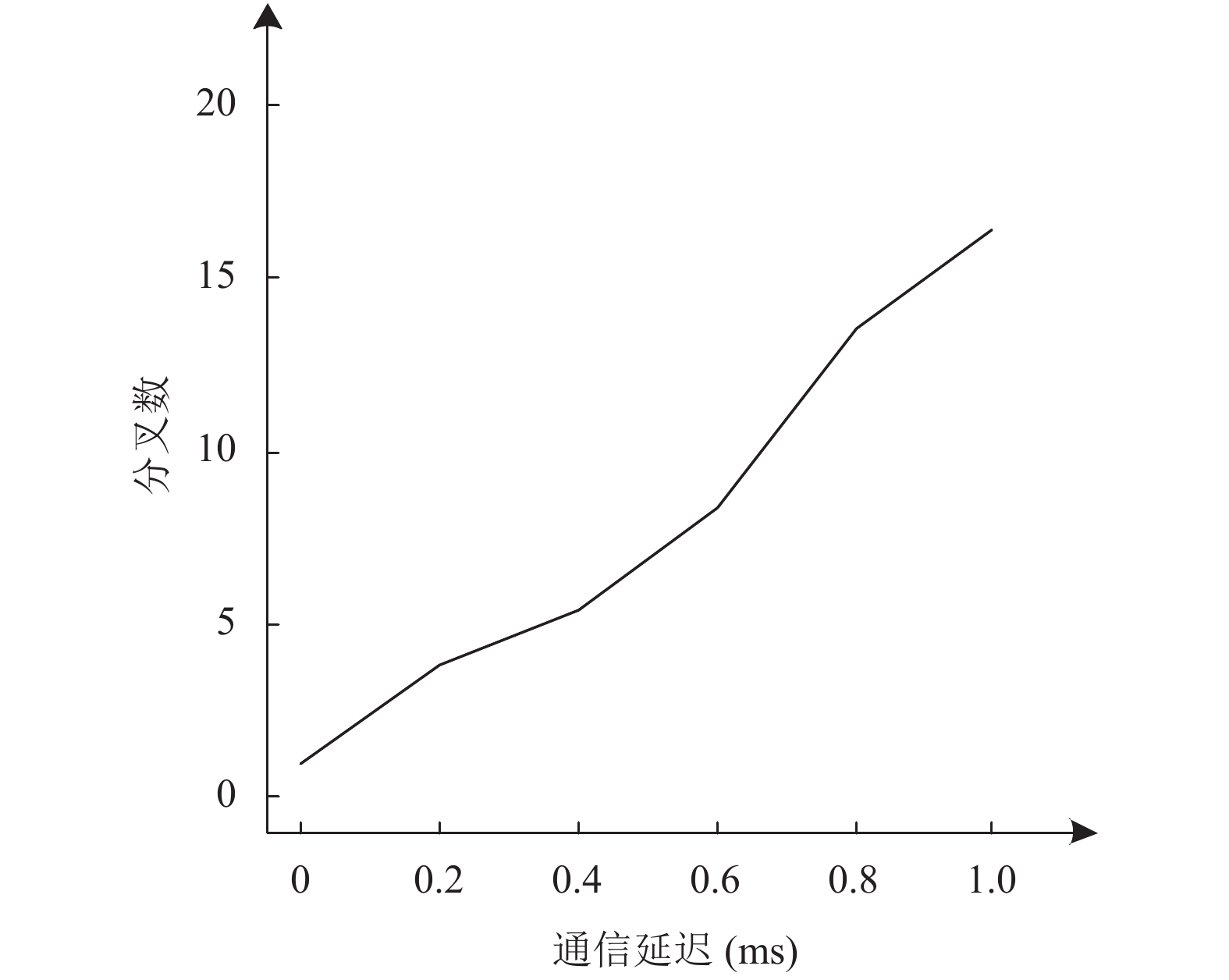
|
图 5 分叉数与通信延迟时间关系 |
|
图 6 交易确认时间与通信延迟时间关系 |
从图6中看出, 随着通信延迟时间的增加, 交易确认时间也随之增加. 在本文中, 没有提供关于区块链实施方案的经济可行性的全面分析. 经济可行性将取决于运营区块链网络的成本和执行智能合约的成本. 然而, 区块链模拟器可以根据区块链网络的计划节点数和带宽预测区块链的性能. 因此, 区块链模拟器可用于估算P2P电能交易平台的运营成本以及确定基于区块链的P2P对等能源交易的经济可行性. 使用区块链模拟器来确定合适的区块链网络的流程图如图7所示.

|
图 7 确定区块链网络流程图 |
如图7所示, 在构建合适的区块链的过程中, 首先要根据区块链的节点数和通信延迟时间确定区块链属性. 这些参数被将被用作区块链仿真器的输入. 然后使用仿真执行的结果确定预期的区块链分叉数和区块链吞吐量. 如果区块链仿真性能令人不满意的话, 则进行修正, 比如增加或减少区块链节点数以及带宽等, 并重复上述步骤.
3 P2P电能交易数学模型 3.1 用户模型本文定义
| ${e_{L,i}} = \left[ {e_{L,i}^1,e_{L,i}^2,e_{L,i}^3, \cdots ,e_{L,i}^T} \right]\;\;\;\;i = 1,2, \cdots ,n$ | (1) |
式中,
用户
| ${e_{{\rm {PV}},i}} = \left[ {e_{{\rm {PV}},i}^1,e_{{\rm {PV}},i}^2, \cdots ,e_{{\rm {PV}},i}^k, \cdots ,e_{{\rm {PV}},i}^{24}} \right]$ | (2) |
因此, 用户
| ${e_{{\rm {net}},i}} = \left[ {e_{{\rm {net}},i}^1,e_{{\rm {net}},i}^2, \cdots ,e_{{\rm {net}},i}^k, \cdots ,e_{{\rm {net}},i}^{24}} \right]$ | (3) |
用户
| $e_{{\rm {net}},i}^k = e_{L,i}^k - e_{{\rm {PV}},i}^k$ | (4) |
当
| $e_{TBP}^k = \sum\limits_{i = 1}^{{N_M}} {e_{{\rm {net}},i}^k} $ | (5) |
| $e_{TSP}^k = \sum\limits_{j = 1}^{{N_Q}} {\left| {e_{{\rm {net}},j}^k} \right|} $ | (6) |
式中, TBP表示买家总购电功率,
本文提出的基于区块链技术的P2P电能交易模型的目标在保证买卖双方获得效益的的基础上, 实现能源高效利用. 电能交易情况分类如下式所示:
| $ \left\{ \begin{array}{l} {e_{TSP}} = 0\;\;\;\;\;\;\;\;\;\;\;\;{{({\text{无内部电力交易}})}}\\ 0 < {e_{TSP}} < {e_{TBP}}\;\;\;\;\;{{({\text{非合作不完全信息博弈}})}}\\ {e_{TSP}} > {e_{TBP}} \ge 0\;\;\;{{({\text{内部电力交易电价为}}}}{p_g}{\rm{)}} \end{array} \right. $ | (7) |
式中, 当
| $S = \left\{ {({N_M} \cup {N_Q}),{{\left\{ {{E_i}} \right\}}_{i \in {N_Q}}},{{\left\{ {{U_i}} \right\}}_{i \in {N_Q}}},P,R} \right\}$ | (8) |
式中, 卖方用户
| $\begin{split} R =& \displaystyle\sum\limits_{j \in {N_M}} {{R_j} = p\displaystyle\sum\limits_{i \in {N_Q}} {({e_{PV,i}} - {e_{L,i}})} } {\rm{ }} \\ & +{p_{gs}}\left[ {\displaystyle\sum\limits_{j \in {N_M}} {({e_{L,j}} - {e_{PV,j}})} - \displaystyle\sum\limits_{i \in {N_Q}} {({e_{PV,i}} - {e_{L,i}})} } \right] \end{split} $ | (9) |
在微电网内买家用户集合的购电费用
| ${w_j} = {e_{TSP}}\frac{{{e_{L,j}} - {e_{PV,j}}}}{{{e_{TBP}}}}\;\;\;\;j \in {N_M}$ | (10) |
为了实现买家的购电费用以及卖家的用电效益最大这一目标, 微电网内的买方用户群会制定最优的内部电价, 同时卖家也会根据这一电价选取最优用电计划. 该博弈
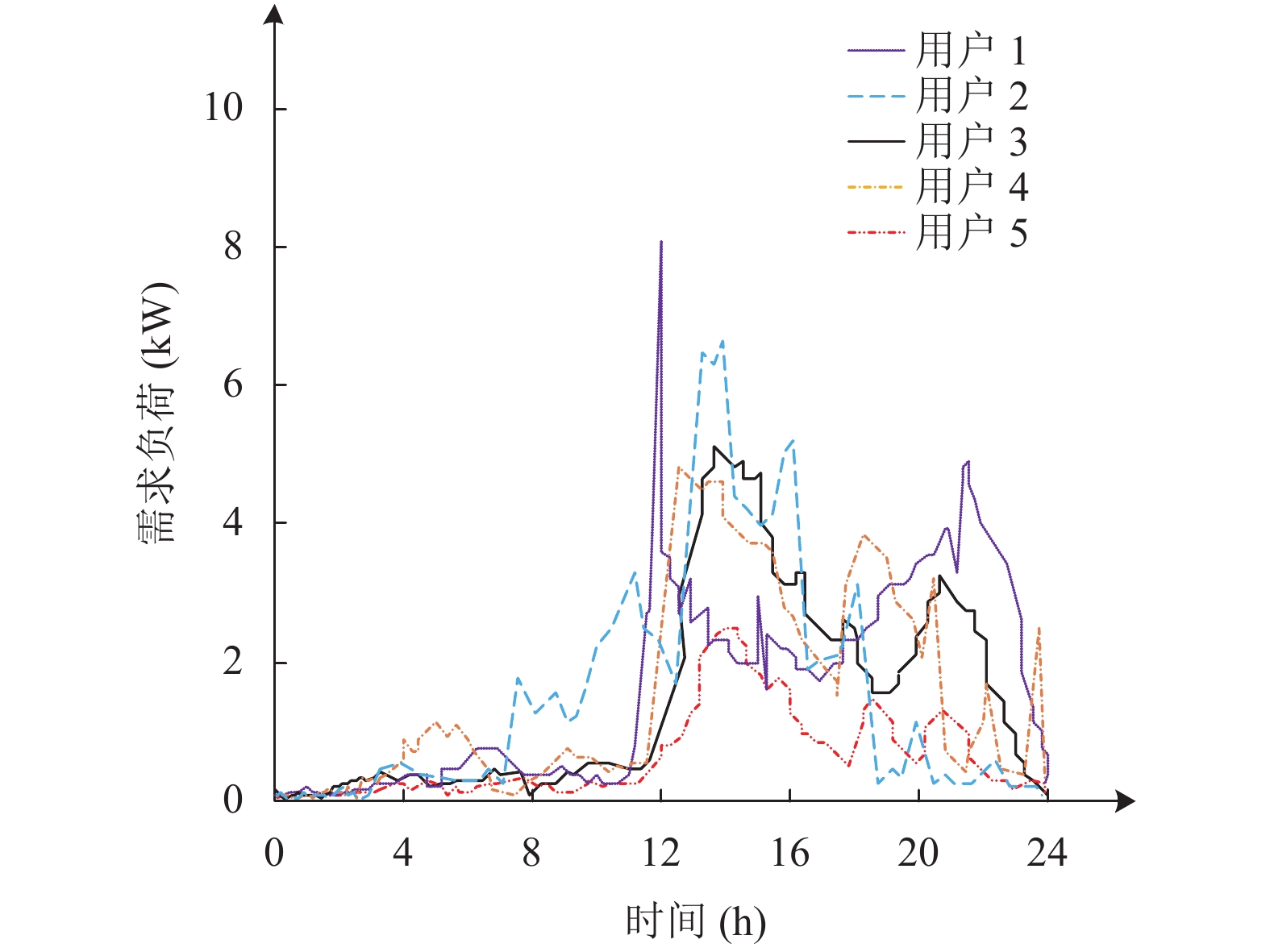
本文通过一个社区微网算例来研究的P2P电能交易平台对配电网的影响. 该社区微网代表了一个典型的三相低压郊区住宅系统, 本文选取了5名用户作为样本. 图8是该样本在一天24 h内需求负荷曲线图. 馈线首端电压设置为固定值, 低压二次网无有功电压调节. 网络由708个节点之间的707个线路对组成的串联阻抗(由电阻和电抗组成). 该社区微网共有55名居民用户, 几乎平均分布在馈线的3段(A段21名用户, B段19名用户, C段15名用户). 仿真过程每隔5分钟计算以下参数: 每个用户连接点的电压、电网各支路有功、无功功率、每条支路中的有功功率损耗、低压违规次数、高压违规次数以及三相电压不平衡度等.
|
图 8 某日用户需求负荷曲线图 |
为了研究分布式能源资源渗透率极高的未来网络场景, 并为P2P电能交易创造条件, 该社区微网中都增加了光伏(PV)发电和电动汽车(EV)充电需求. 住宅光伏单元视为每个负载点的有功功率注入. 光伏发电机组容量在1.6 – 4 kW之间, 采用最大功率点跟踪, 并以固定单位功率因数运行. 本文使用的电动汽车充电数据来源于实际汽车充电数据, 其中每个电动汽车充电器的额定功率为3 kW. 表1列出了安装的PV和EV容量.
| 表 1 PV和EV数量及其额定容量 |
通过配电网仿真分析某一天中电网的功率流和电压的变化. 本文为了方便进行比较研究, 分析了以下两种情况:
场景一. 在不进行P2P电能交易的情况下, 利用图7所示的需求负荷曲线、EV充电需求和PV发电输出功率进行配电网仿真.
场景二. 基于P2P电能交易平台的基础上, 采用与场景一相同的输入数据, 和本文提出的基于分布式双边拍卖机制, 进行P2P电能交易与配电网的协同仿真.
4.2 算例结果分析OpenDSS网络仿真中记录的有功、无功输入/输出情况如图9、图10所示. 由于该算例研究具有非常高的PV渗透率, 因此在一天的中午, 变电站有一个净输出, 此时有功及无功功率皆为负值. 本文假设低压网络能够适应双向潮流. P2P电能交易的最大交易量发生在17:00到20:00 之间, 如图9和图10中的虚线所示. 可以看出, 在这段时间里, P2P电能交易对有功功率和无功功率影响较大.
表2给出了配电网仿真的数据结果. 这些结果表明, 在P2P情况下, 配电网的净输出在一天中增加了约19 kWh. 无功电量减少6 kvarh以上. P2P能源交易最大复功率和网络有功功率损失均无显著变化. P2P能源交易对配电网电压的影响也可以通过电压不平衡度来测量. 本文定义相位电压不平衡率(PVUR)为平均相位电压的最大电压偏差占平均相位电压的百分比. 如表2所示, 与场景一相比, 场景二的PVUR略微降低.
| 表 2 配电网仿真结果 |
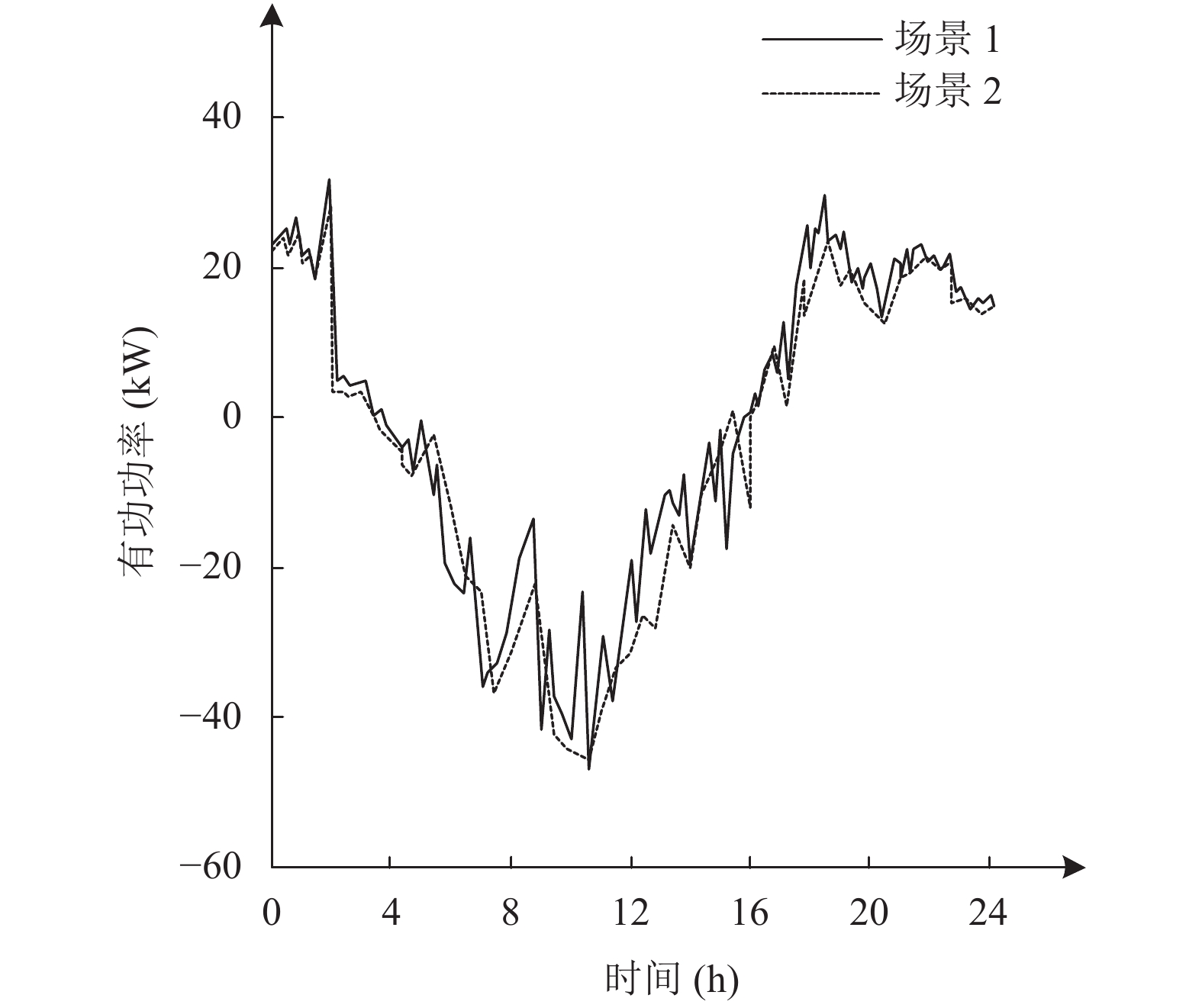
|
图 9 场景一和场景二有功功率对比 |
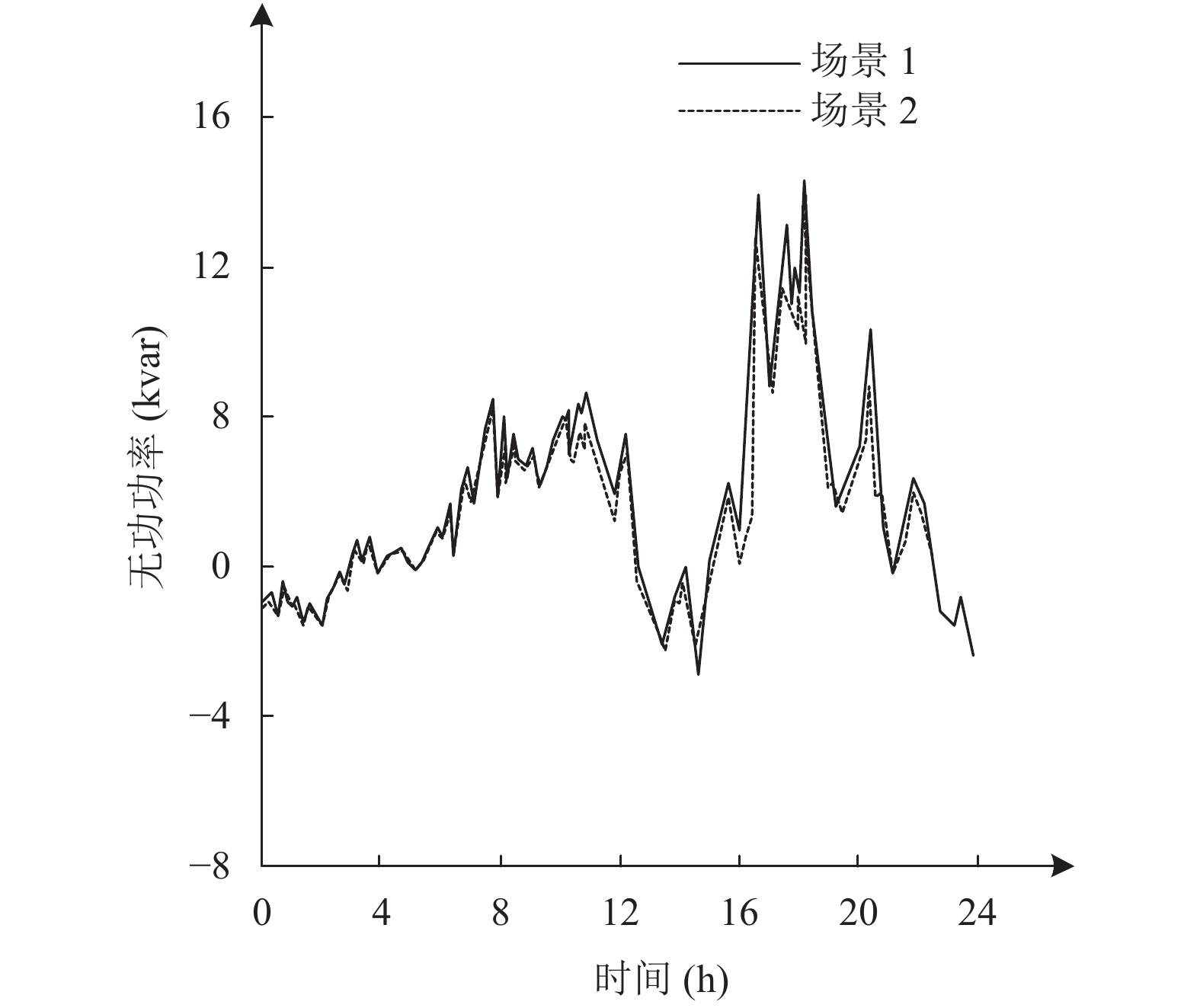
|
图 10 场景一和场景二无功功率对比 |
图11是场景一和场景二电压分布差异示意图, 以百分比值表示. 从图中可以看出, P2P电能交易对电压影响最显著的时间段是17:00–20:00.
仿真结果表明, 在该算例中, 中等水平的P2P电能交易对配电网运行性能没有显著影响. 从表2中可以看出, 最大复功率没有受到显著影响, 场景一和场景二的差异小于1 kVA. 图11的结果显示, 即使在P2P电能交易对电压影响最显著的时间段, 电压分布也只有微小的差异.

|
图 11 场景一和场景二电压分布差异 |
5 结论
本文在基于区块链和能源互联网的条件下, 提出了一种基于区块链技术的P2P电能交易市场机制与配电网协同仿真的框架. 采用分布式双边拍卖技术和智能合约, 通过建立的数学模型和博弈模型对P2P电能交易机制进行了仿真分析. 与传统的电力市场交易模式相比较, P2P电能交易模式减少了不必要的电力损耗, 使资源成本和交易成本最小化. 在算例分析中, 设置了场景一和场景二, 通过两个场景的仿真分析结果, 从功率和电压两个方面研究了P2P电能交易对配电网运行的影响并验证了其潜在效益. 本研究对推动区块链在电能交易中的落地应用、保证用电安全稳定、实现能源平衡以及使得与区块链相结合的P2P能源交易机制获得更大范围的接受有着重要意义.
| [1] |
谢敬东, 陆池鑫, 孙欣, 等. 区块链技术在能源与电力系统领域的应用和展望. 电测与仪表, 2020. 1–12. (2020-07-07)[2020-07-15].
|
| [2] |
朱文广, 熊宁, 钟士元, 等. 基于区块链的配电网电力交易方法. 电力系统保护与控制, 2018, 46(24): 165-172. |
| [3] |
Andoni M, Robu V, Flynn D, et al. Blockchain technology in the energy sector: A systematic review of challenges and opportunities. Renewable and Sustainable Energy Reviews, 2019, 100: 143-174. DOI:10.1016/j.rser.2018.10.014 |
| [4] |
王立棋, 杨庆, 王静, 等. 基于区块链下光伏微电网交易市场化中的应用分析. 电测与仪表, 2020, 57(12): 75-82. |
| [5] |
邰雪, 孙宏斌, 郭庆来. 能源互联网区块链应用的交易效率分析. 电网技术, 2017, 41(10): 3400-3406. |
| [6] |
Ma JH, Deng J, Song LY, et al. Incentive mechanism for demand side management in smart grid using auction. IEEE Transactions on Smart Grid, 2014, 5(3): 1379-1388. DOI:10.1109/TSG.2014.2302915 |
| [7] |
Liu N, Yu XH, Wang C, et al. Energy-sharing model with price-based demand response for microgrids of peer-to-peer prosumers. IEEE Transactions on Power Systems, 2017, 32(5): 3569-3583. DOI:10.1109/TPWRS.2017.2649558 |
| [8] |
Marzband M, Azarinejadian F, Savaghebi M, et al. Smart transactive energy framework in grid-connected multiple home microgrids under independent and coalition operations. Renewable Energy, 2018, 126: 95-106. DOI:10.1016/j.renene.2018.03.021 |
| [9] |
Kang JW, Yu R, Huang XM, et al. Enabling localized peer-to-peer electricity trading among plug-in hybrid electric vehicles using consortium blockchains. IEEE Transactions on Industrial Informatics, 2017, 13(6): 3154-3164. DOI:10.1109/TII.2017.2709784 |
| [10] |
李鹏, 孙充勃, 王成山, 等. 基于OpenDSS的智能配电网仿真与模拟平台及其应用. 中国电力, 2013, 46(11): 12-16. DOI:10.3969/j.issn.1004-9649.2013.11.003 |
| [11] |
McAfee R. A dominant strategy double auction. Journal of Economic Theory, 1992, 56(2): 434-450. |
| [12] |
路军, 王志国, 杨庆, 等. 基于区块链的光伏微电网交易的博弈模型研究. 电测与仪表, 2020, 57(11): 80-86. |
 2021, Vol. 30
2021, Vol. 30


