目前英语考试智能组卷多以计算机自动组卷技术为主, 计算机自动组卷技术能够按照用户的组卷需求, 在计算机题库里选取英语试题构建一套满足用户需求的英语试卷. 计算机自动组卷技术能够降低人力物力的投入, 优化英语考试组卷质量与效率.

组卷问题属于一类多目标优化问题, 研究一种满足组卷需求的智能组卷方法, 是完成计算机智能组卷的核心, 存在一定研究价值.

诸多学者为了提高组卷的水平对此进行了研究, 并取得了一定成果. 例如, 李瑞森等人^[1]针对试题库建设需求, 提出了一种自底向上的试题库建设方案, 研究了试卷图形化交互布局; 杜明等人^[2]针对信息化发展中在线试卷的组卷工作中存在的问题, 设计了基于知识水平的改进智能遗传组卷算法; 此外, 潘婷婷等人^[3]研究了基于知识点权重与错误率关联的个性化训练模型, 提高组卷水平.

和声搜索算法能够对多目标优化问题存在较好的求解功能, 但是传统的和声搜索算法易进入局部最优, 求解精度有待考证. 为此, 本文提出基于改进和声搜索算法的英语考试智能组卷策略, 该方法中采用的和声搜索算法为离散和声搜索算法, 并对离散和声搜索算法进行改进, 使算法不易陷入局部最优. 而且本文策略在求取英语考试智能组卷最优解时, 题库试题质量较好; 并且在计算机自动组卷后, 种群多样性在组卷前期都较高, 伴随迭代次数增多, 组卷后期本文策略种群多样性快速降低, 能够快速获取全局最优解.

1 基于改进和声搜索算法的英语考试智能组卷策略 1.1 英语考试智能组卷多目标优化模型

将英语考试知识点属性 ${\varphi _1}\left( y \right)$ 设成:

${\varphi _1}\left( y \right) = \frac{1}{m}\sum\limits_{j = 1}^m {{B_j}} $

(1)

其中, 组卷任务的英语试题总量是m, 第j个英语试题涵盖的知识点比例是B_j, ${B_j} = \dfrac{{{S_j}}}{{{S_{\rm {total}}}}}$ ; S_j是第j个英语试题涵盖的知识点数目, S_total是知识点的总数量.

难度属性可以描述英语试题难度 ${\varphi _2}\left( y \right)$ :

${\varphi _2}\left( y \right) = \frac{1}{m}\sum\limits_{j = 1}^m {\exp } \left[ { - \pi {{\left( {{y_j} - \phi } \right)}^2}} \right]$

(2)

${Q_1} = 1 - \frac{{{{\overline Y}_K} + {{\overline Y}_Z}}}{{2U}}$

(3)

${Q_2} = 1 - \frac{G}{P}$

(4)

其中, Q₁、Q₂分别是主观类、客观类英语试题的难度; 高分组、低分组的得分均值依次是 ${\overline Y_K}$ 、 ${\overline Y_Z}$ ; 此英语试题的总分值与本试题答对的人数依次是U、G; 参与英语考试的所有人数是P; 组卷人设置的难度值是 $\phi $ , $\phi $ 值较大, 英语试题难度较高; y_j表示第j个试题的难度水平.

区分度属性能够判断英语试题得分程度^[4-6]. 区分度属性设成 ${\varphi _3}\left( y \right)$ :

${\varphi _3}\left( y \right) = \frac{1}{m}\sum\limits_{j = 1}^m {\exp } \left[ { - \pi {{\left( {{y_j} - \gamma } \right)}^2}} \right]$

(5)

${y_j} = \frac{{{{\overline Y}_K} - {{\overline Y}_Z}}}{U}$

(6)

其中, 是 $\gamma $ 组卷人设定的区分度值, 其值越大, 代表英语试题得分高低差距越显著.

时间期望属性能描述一套英语考试时间多少, 英语考试完成时间与组卷设定的时间较为靠近, 则英语考试智能组卷的时间质量较优^[7]. 试卷时间期望属性 ${\varphi _4}\left( y \right)$ 具体设定是:

${\varphi _4}\left( y \right) = \left\{ {\begin{array}{l} {\displaystyle\sum\limits_{j = 1}^m {\dfrac{{{H_j}}}{{H{}_{\rm {total}}}}} },\;\; {\displaystyle\sum\limits_{j = 1}^m {\dfrac{{{H_j}}}{{H{}_{\rm {total}}}} \le 1} } \\ {0\mathop {}\nolimits_{}^{} ,\;\; {\displaystyle\sum\limits_{j = 1}^m {\dfrac{{{H_j}}}{{H{}_{\rm {total}}}} > 1} } } \end{array}} \right.$

(7)

其中, 第j个英语试题耗费的期望时间是H_j, H_j值由组卷人设置; H_total是整体测试时间.

为了优化组卷质量, 构建的模型需要以上述属性为核心, 构建英语考试智能组多目标优化函数是:

$\varphi \left( y \right) = \max \left( {\sum\limits_{j = 1}^4 {{\varpi _j}{\varphi _j}\left( y \right)} } \right)$

(8)

其中, 每个子函数的权重是 ${\varpi _j}$ .

1.2 基于改进和声搜索算法的组卷最优解求解方法

英语考试智能组卷属于离散问题, 必须采用离散和声搜索算法求解式(8), 获取组卷最优方案^{[8, 9]}. 离散和声搜索算法先初始化和声记忆库, 各个组卷难度决策变量的值域设成 ${Y_j}\left( {{y_j}\left( 1 \right),{y_j}\left( 2 \right),\cdots,{y_j}\left( L \right)} \right)$ , 组卷难度决策变量可能取值的数量设成L. 在离散和声搜索算法各次迭代时, 对 $\varphi \left( y \right)$ 进行求解, 获取智能组卷策略的可行解集合 ${y^{\rm {new}}} = \left( {y_1^{\rm {new}},y_2^{\rm {new}},\cdots,y_M^{\rm {new}}} \right)$ , $y_M^{\rm {new}}$ 表示M个可行解. 新的智能组卷策略可行解获取方法是:

$ {y}_{M}^{\rm {new}}=\left\{ {\begin{array}{l} {y}_{M}^{\rm {new}}\left({\phi }_{j}\left(y\right)\right),{\rm {i{f}}}\;rand<HMCR\\ {y}_{M}^{\rm {new}}\left({\phi }_{j}\left(y\right)\right)\in {Y}_{j},{\text{其他}}\end{array}} \right.$

(9)

其中, rand表示[0 1]间的随机数, 通过rand产生一个[0 1]间的随机数, 然后将HMCR与该随机数进行比较, 根据比较结果产生新的新和声. HMCR表示和声记忆库取值(题库使用)概率.

调整和声记忆库(Harmony Memory, HM)中的新和声 $y_M^{\rm {new}}$ :

$ {y}_{M}^{\rm {new}}=\left\{ {\begin{array}{l}{y}_{M}^{\rm {new}}\left(h+n\right),n\in \left\{-1,1\right\},{\rm {i{f}}}\;rand<PAR\\ {y}_{M}^{\rm {new}},{\text{其他}}\end{array}} \right.$

(10)

其中, 音调(英语试题)调整概率是PAR; h、n分别代表一维变量与组卷的干扰变量. 若获取的新和声比HM中最劣和声好, 把最劣和声换成新和声. 当迭代次数达到最大值后, 算法停止^[10].

离散和声搜索算法流程是:

(1) 设定离散和声搜索算法参数: 和声记忆库(题库)的大小HMS、音调(英语试题)调整概率PAR、和声记忆库取值(题库使用)概率HMCR与迭代次数最大值N.

(2) 在组卷难度决策变量可能取值的整数区间中任意建立多个和声, 运算相应的和声适应度值 $\Omega \left( {{y_1},{y_2}} \right)$ , 适应度值能够体现题库试题的优劣, 将和声记忆库实施初始化处理^{[11, 12]}.

$\Omega \left( {{y_1},{y_2}} \right) = 0.5 - \frac{{\left( {{{\sin }^2}\sqrt {y_1^{} + y_2^{}} - 0.5} \right)}}{{{{\left[ {1 + 0.001\left( {y_1^{} + y_2^{}} \right)} \right]}^2}}}$

(11)

其中, y₁、y₂依次表示英语试卷第1道题与第2道题的优劣变量.

(3) 使用式(9)获取一个新和声. 使用式(11)调整HM中新和声. 如果新和声比HM中最劣和声优, 把最劣和声换成新和声, 运算相应和声适应度值, 刷新HM.

(4) 如果迭代次数为最大值, 算法停止; 反之回到第(2)步.

因为离散和声搜索算法运行时, 各次迭代仅可以使用和声记忆库的一个新和声, 新和声与HM里最劣的和声相比之下, 若新和声比HM中最劣和声优, 把最劣和声换成新和声, 实现HM更新. 此类方法属于单个体更新处理, HM中的信息不能被充分使用, 且算法具有非固定搜索属性, 获取的智能组卷新解伴随迭代次数的增多, 难以存储于和声记忆库中, 和声搜索算法的局部搜索性能将变差^[13]. 为此, 本文对此问题进行优化, 优化模式如下:

(1) 个性记忆考虑过程. 在个体记忆考虑过程中可以全面使用HM中的全部积累信息. 因为传统和声搜索算法是一种维记忆考虑模式, 记忆仅对和声的部分维而言具备有效性. 本文中, 个体记忆考虑过程需要将各个个体实施全局记忆考虑. 部分维记忆的模式将有损于和声信息的完整度, 但个体记忆考虑过程对和声信息的完整度不存在损坏^[14]. 算法在各次迭代时, 在已有和声集合y^j中建立一个相应的新和声 $y_1^{\rm {new}}$ , 通过优胜劣汰的模式将 $y_1^{\rm {new}}$ 和HM中最劣和声 $y_1^{\rm {worst}}$ 实施更新. 在HM外随机设定一个收敛因子 ${v_j}$ , 防止算法进入局部最佳, 获取的新解是:

$y_M^{\rm {new}} = \left\{ {\begin{array}{*{20}{l}} {y_M^{\rm {new}},}&{{\rm {if}}\;\; {v_1} < HMCR} \\ {y_M^{\rm {new}} \in {Y_j},}&{{\rm {if}}\;\; {v_1} \ge HMCR} \end{array}} \right.$

(12)

其中, ${v_1} \in {v_j}$ . 若 ${v_1} < HMCR$ , 把 ${y^j}$ 中的和声设成新和声 $y_1^{\rm {new}}$ , $y_1^{\rm {new}} = y_M^{\rm {new}}$ . 若将HM中第2个和声建立一个新的组卷解, 新解存在HMCR的概率, HM中第二个和声即为新和声. 为了优化算法全局搜索性能, 稳定和声记忆库中的种群多样化, 新解存在 $1 - HMCR$ 的概率属于值域中随机值.

(2) 扰动搜索过程. 扰动搜索过程为局部搜索, 存在较显著的局部搜索性能. 能够调整音调, 在小范围中获取和声最优解, 不会进入局部最优^[15].

若新解属于HM, 使用音调调整概率PAR将y^new的各维变量实施调整搜索:

$y_M^{\rm {new}} = \left\{ {\begin{array}{*{20}{l}} {y_M^{\rm {new}} = h,}&{{\rm {if}}\;\; {v_2} < PAR} \\ {y_M^{\rm {new}},}&{{\rm {if}}\;\; {v_2} \ge PAR} \end{array}} \right.$

(13)

$h = \left\{ {\begin{array}{*{20}{c}} { - 1,}&{{\rm {if}}\;\; {v_3} < 0.5} \\ {1,}&{{\rm {if}}\;\; {v_3} \ge 0.5} \end{array}} \right.$

(14)

其中, ${v_2} \in {v_j}$ , ${v_3} \in {v_j}$ .

(3) 竞争淘汰机制. 因为更新HS是在新解与最劣解之间实现竞争更新, HM中信息更新效率低. 为此改进和声搜索算法使用竞争淘汰机制, 将和声记忆库实施更新. 在竞争淘汰机制里, 各个新解与HM中相应的最劣解实施竞争. 竞争淘汰机制可以提升HM中优胜劣汰的速度, 优化单个个体与和声库的整体质量, 将新和声实施优劣评价, 以此实现和声记忆库的更新. 更新方法是:

$\left\{ {\begin{array}{*{20}{l}} {y_{}^j = y_M^{\rm {new}},}&{{\rm {if}}\;\; y_M^{\rm {new}} < y_{}^j} \\ {y_1^{\rm {worst}} = y_1^{\rm {new}},}&{{\rm {if}}\;\; y_{}^j < y_1^{\rm {new}} < y_1^{\rm {worst}}} \end{array}} \right.$

(15)

使用此类竞争淘汰机制提高HM全局往最优解靠近的效率.

2 仿真实验

为了测试本文基于改进和声搜索算法的英语考试智能组卷策略对英语考试试卷的智能组卷有效性, 以2019年辽宁省英语四级考试的试卷为例, 该省相关组卷机构使用计算机自动组卷系统进行智能组卷, 在该系统中引入本文策略进行组卷. 使用Java语言编程进行程序编写, 实验环境是Windows XP系统, 处理器为851 MHz, 内存为64 MB. 2019年某省英语四级考试的题库里全部试题的知识点均值、难度均值、区分度均值依次设成0.65、0.52、0.63.

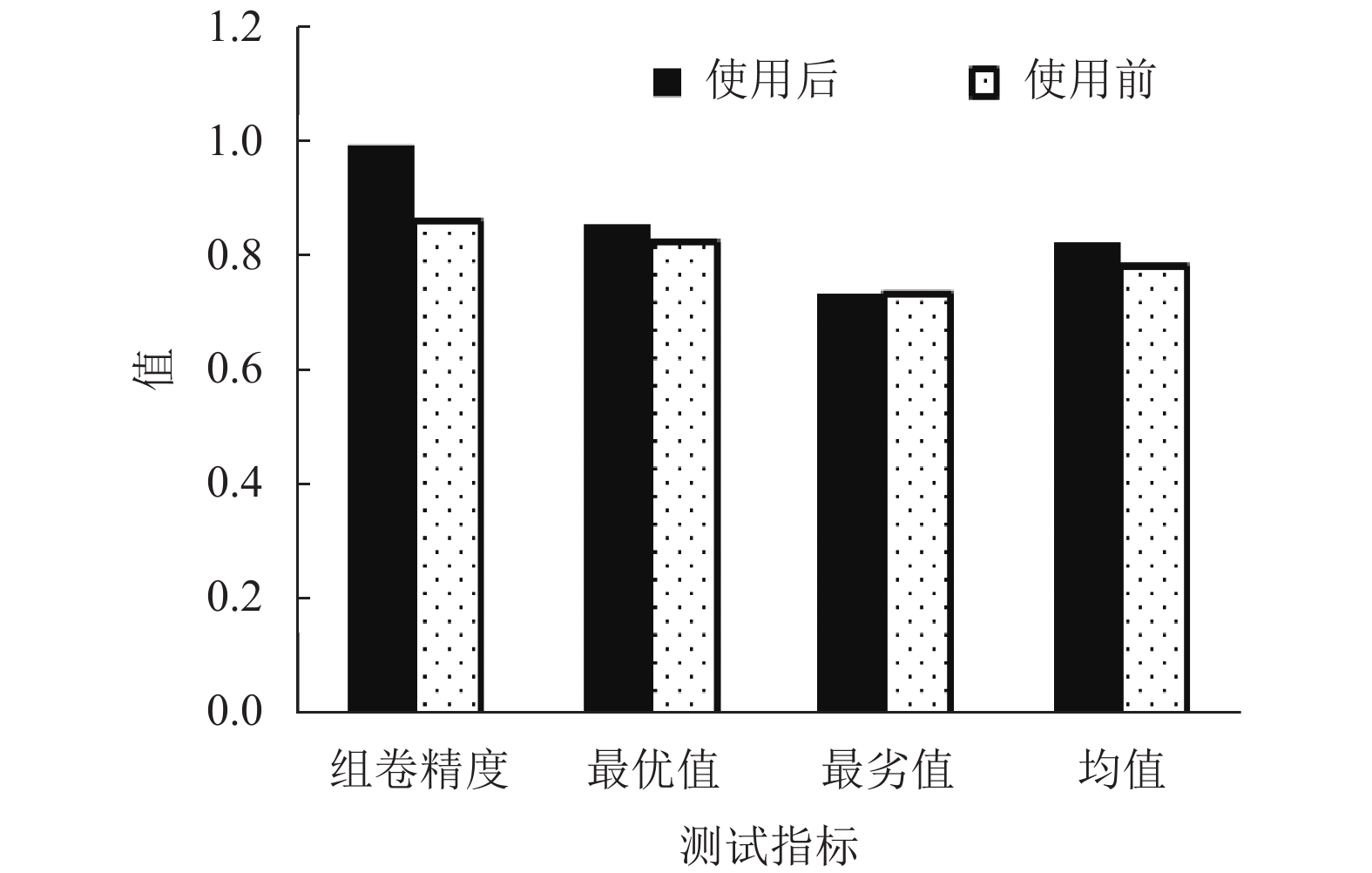
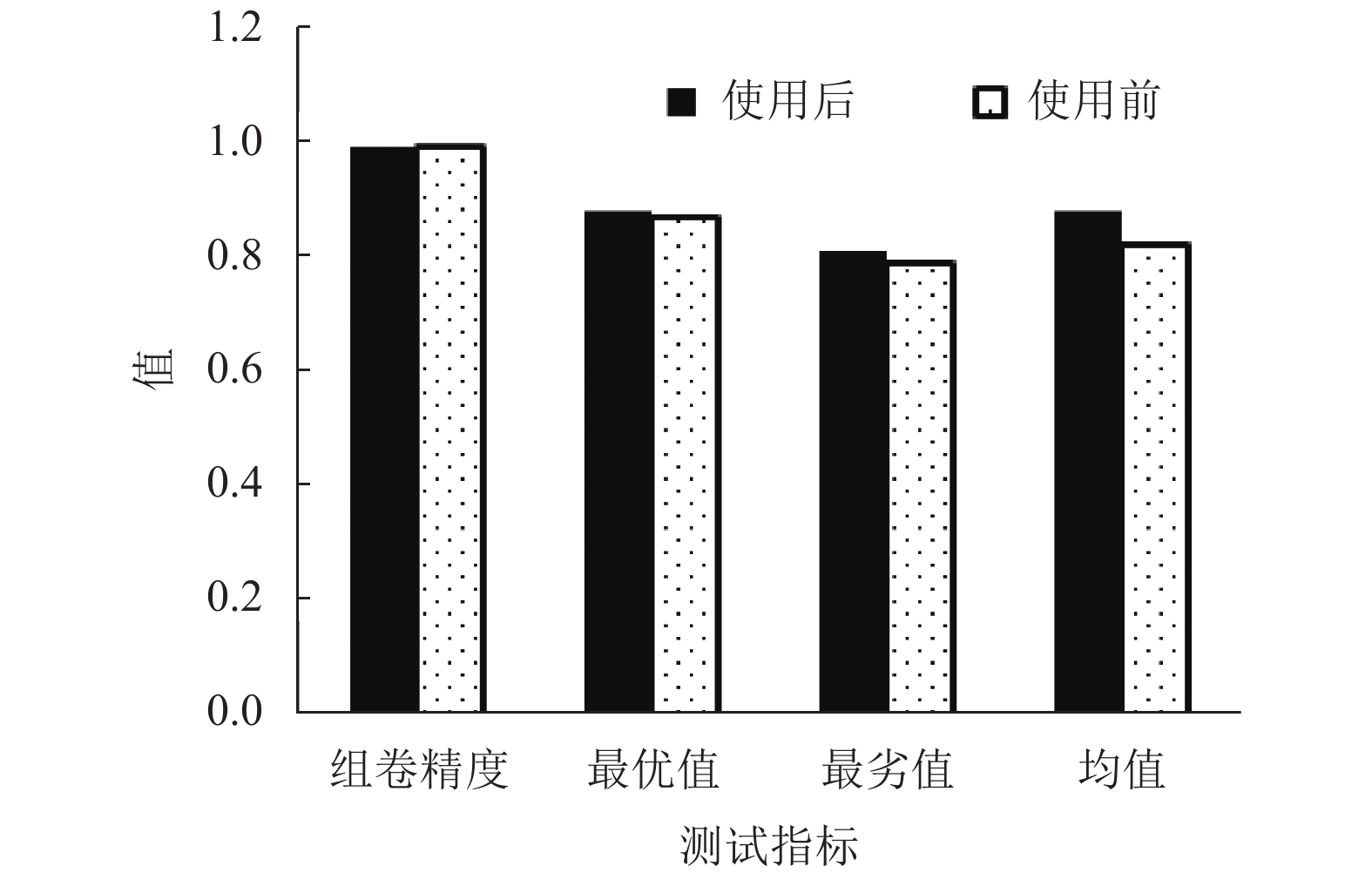
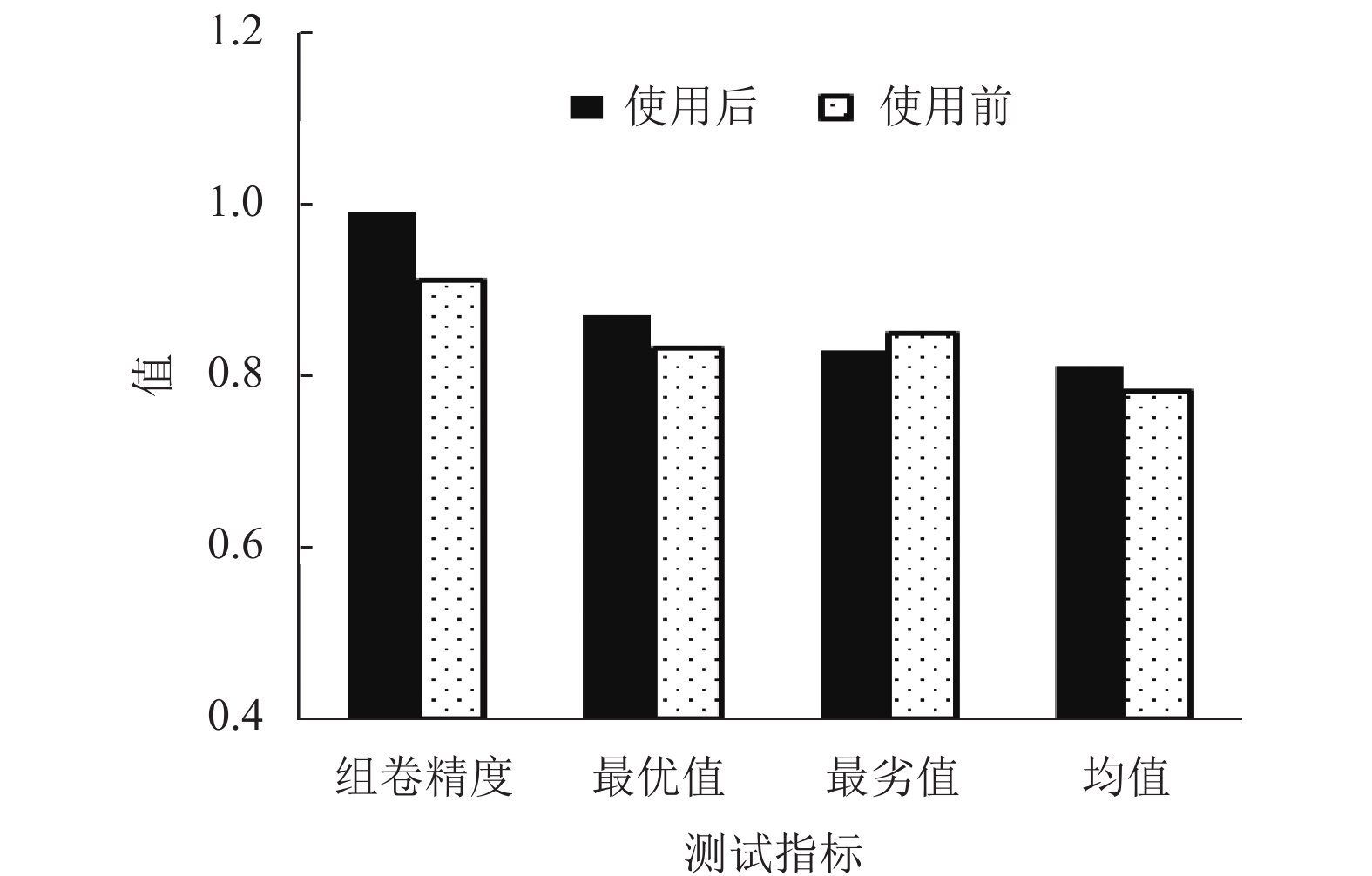
2.1 不同试卷期望时间下组卷效果分析

试卷分数总值是100分, 填空题分数是12分, 选择题分数是32分, 名词解释分数是12分, 简答题分数是22分, 综合题分数是22分. 设定试卷预期完成3个时间段指标上下限值分别是30–60 min、61–90 min、91–120 min, 3个时间段的组卷效果如图1、图2、图3所示. 组卷精度表示本文策略使用前后, 计算机自动组卷40次获取组卷策略可行解的概率; 最优值、最劣值、均值依次是本文策略组卷40次后, 计算机自动组卷系统获取可行解质量的最优值、最劣值、均值. 图1、图2、图3中, 使用本文策略前, 计算机自动组卷系统获取3个时间段可行解的概率依次是0.86、0.99、0.91; 本文策略使用后, 计算机自动组卷获取可行解的概率都是0.99. 且本文策略使用后, 计算机自动组卷40次获取可行解的最优值、均值大于使用前.

2.2 试卷种群适应度分析

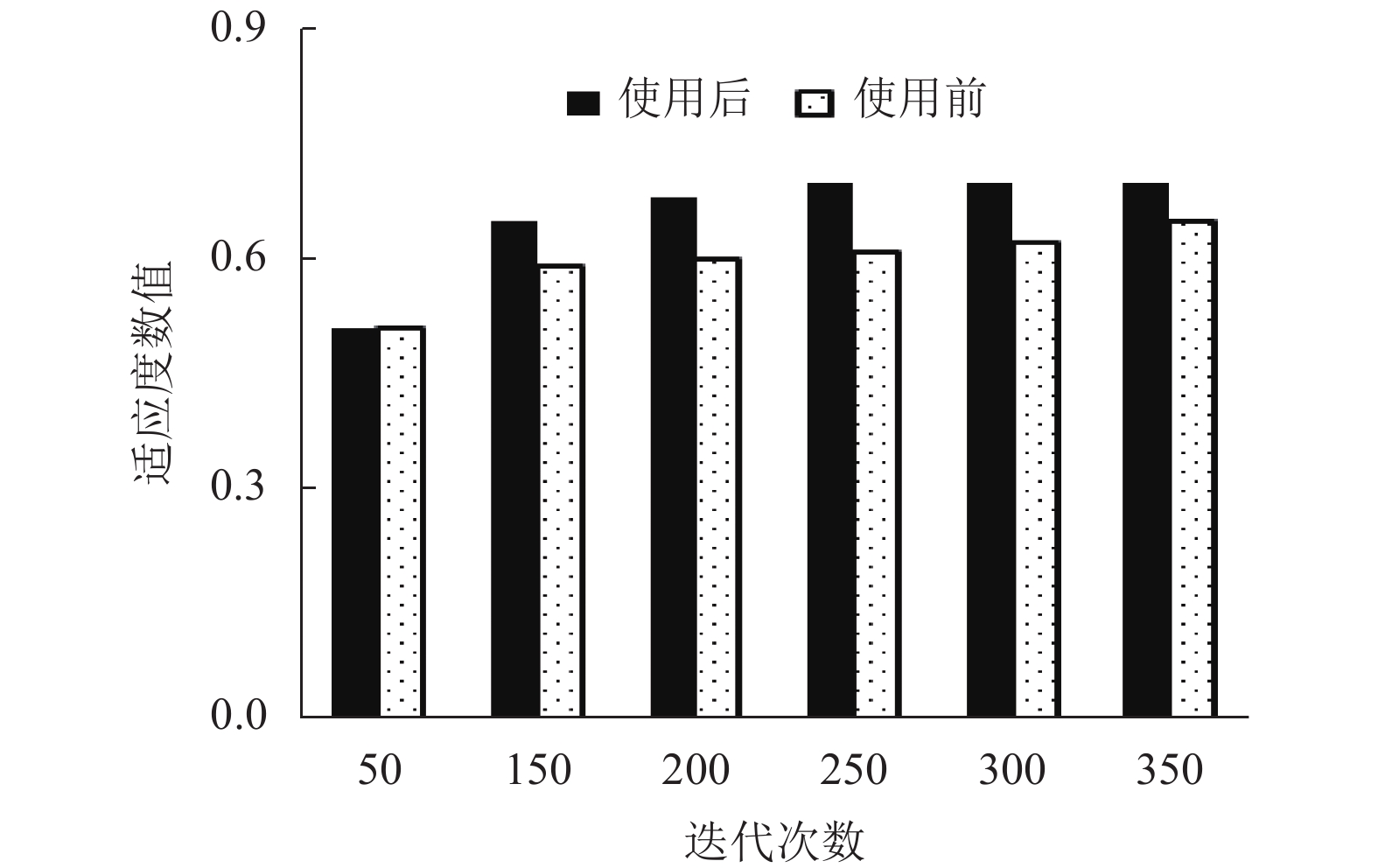
设定本文基于改进和声搜索算法的英语考试智能组卷策略在求取英语考试智能组卷策略的最优解时, 和声记忆库中种群的个体数量都是100个, 迭代次数为350次. 本文策略使用前后的适应度最大值如图4所示. 分析图4可知, 本文策略使用后的适应度最大值为0.70, 使用前的适应度值是0.65, 则使用本文策略求取英语考试智能组卷最优解时, 题库的试题质量较好.

2.3 试卷种群多样性分析

试卷种群的多样性可表示题库试题间的差异水平. 试题差异较大, 种群多样性较高, 否则, 种群多样性较低, 试题差异较小. 种群多样性计算方法是:

$\Gamma = \frac{1}{h}\sum\limits_{j = 1}^h {\sqrt {\frac{1}{{HMS}}\sum\limits_{j = 1}^{HMS} {\left( {y_M^{\rm {new}} - {{\overline y}_i}} \right)} } } $

(16)

其中, 题库中第j套智能组卷的最优解种类均值为 ${\overline y_j}$ ; $h$ 为维数.

针对和声搜索算法而言, 种群的多样性和算法的搜索性能存在直接影响, 如果种群多样性较大, 算法的整体搜索性能较优, 能够探索未曾探索过的搜索范围, 用在本文研究内容中, 可理解成能够获取新题型. 但是, 若种群多样性始终较大, 获取全局最优解的难度便提升, 因此在搜索开始阶段, 种群需要存在较好的种群多样性, 搜索后阶段, 为了得到准确的全局最优解, 种群需要往最优解靠拢, 种群的多样性需要逐渐变小.

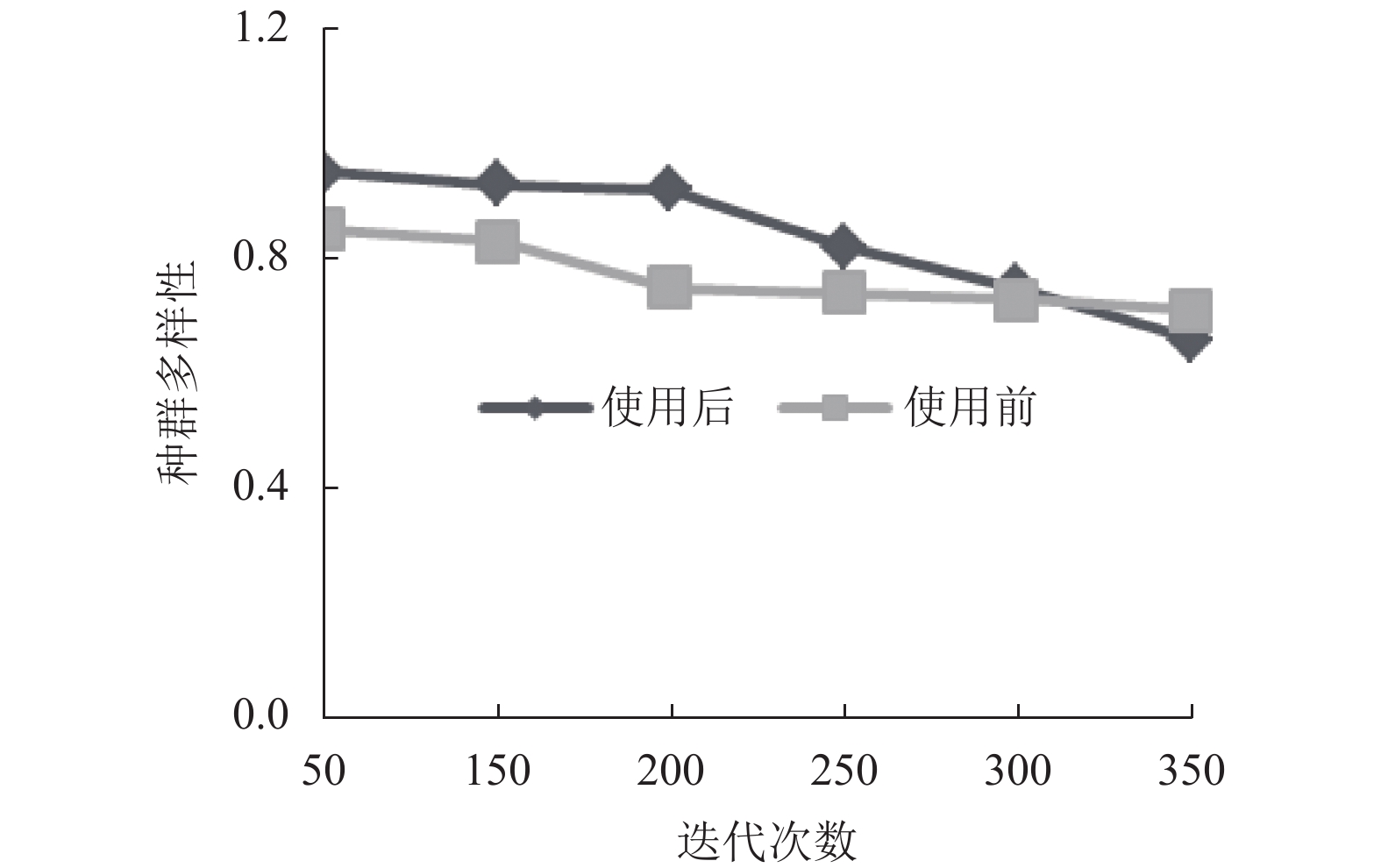
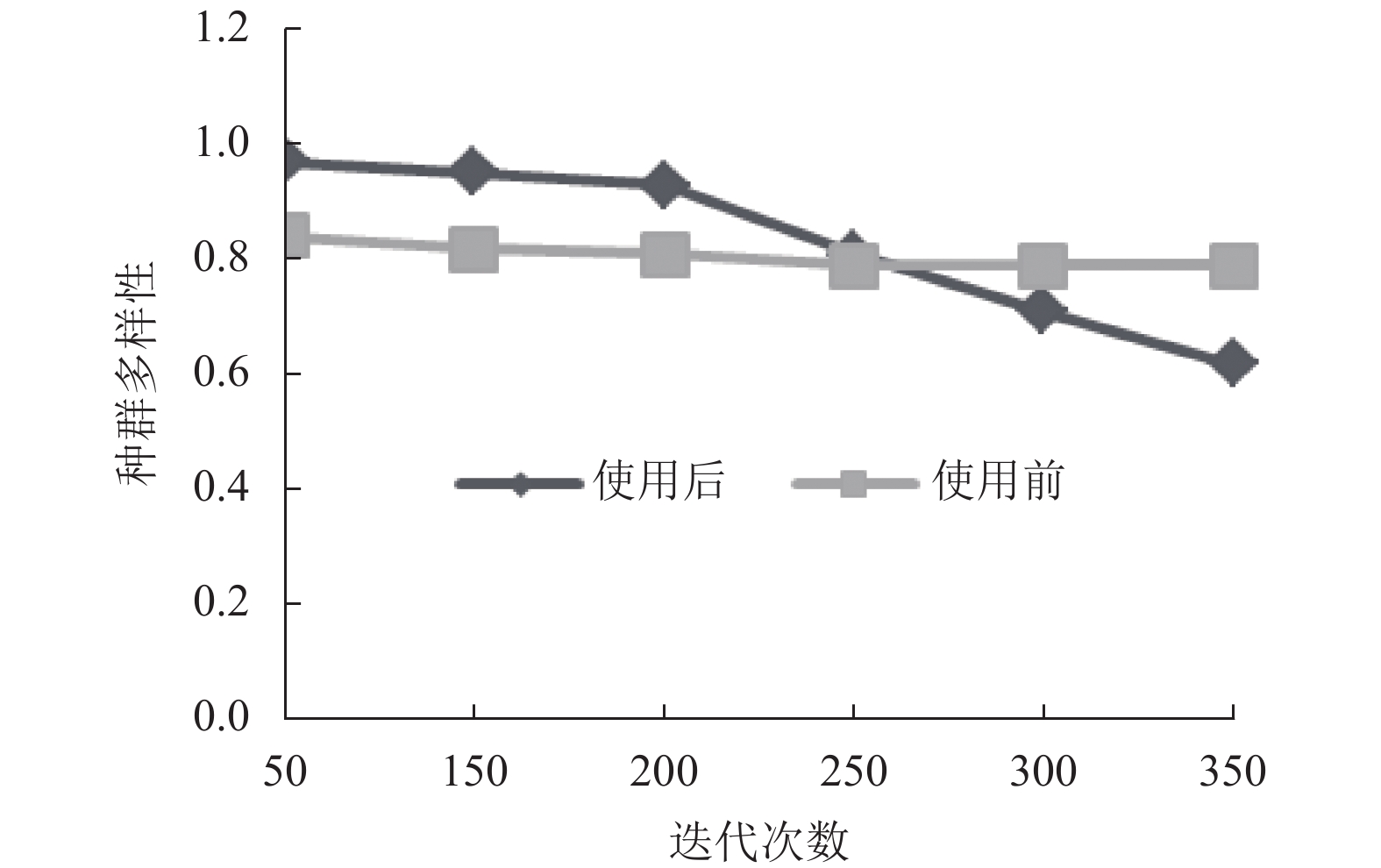
测试本文策略使用前后, 计算机自动组卷系统智能组卷后的种群多样性, 设定需要组卷的试题时间分别是30–60 min、91–120 min, 结果如图5、图6所示. 分析图5、图6可知, 英语考试时间存在约束时, 本文策略使用下, 计算机自动组卷后, 种群多样性在组卷前期都较高, 伴随迭代次数增多, 组卷后期本文策略种群多样性快速降低, 能够快速获取全局最优解. 相比之下, 使用本文策略后, 计算机自动组卷性能较佳.

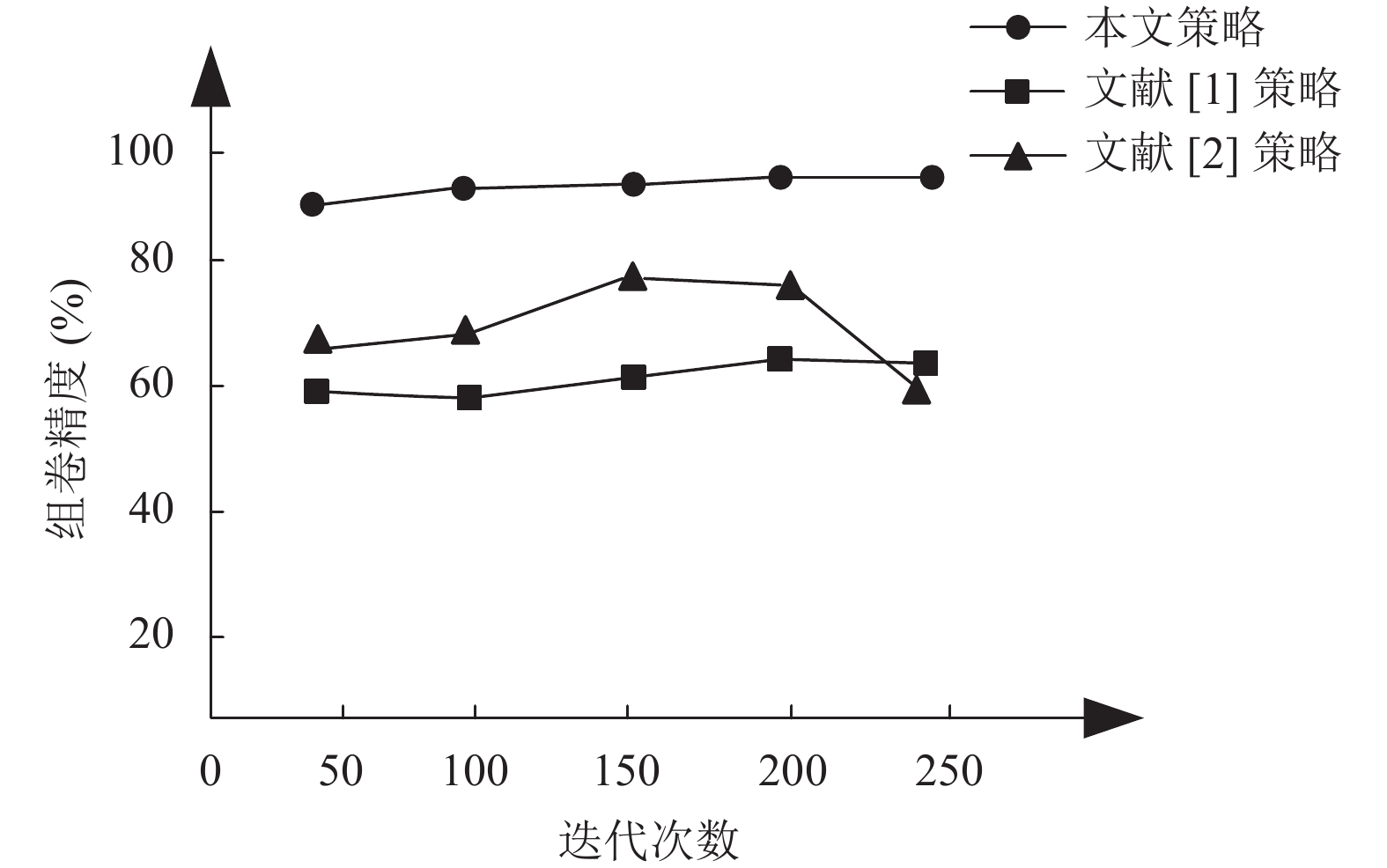
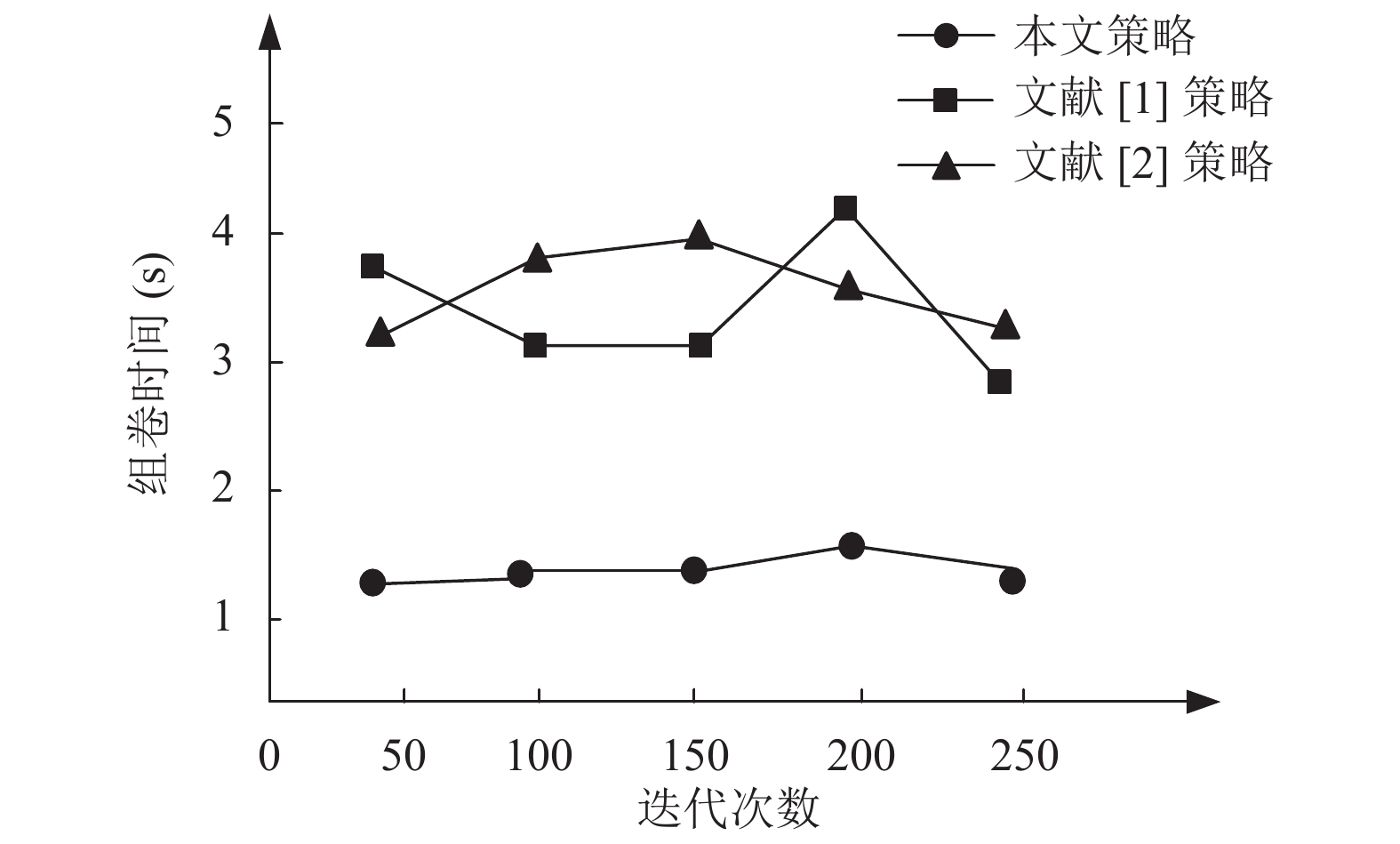
为了进一步证明本文策略的有效性, 采用文献[1]、文献[2]策略与本文策略进行对比. 对比方向为组卷精度以及组卷时间, 比较结果分别如图7、图8所示.

根据图7、图8对比结果可以清晰看出, 无论在50、100、150、200还是250次迭代次数中, 本文策略的组卷精度明显高于另外两种策略, 精度最高可达97%, 而从组卷时间也可以看出, 采用本文策略组卷的组卷时间明显低于另外两种方法, 有效证明了本文策略的有效性.

3 结束语

以英语考试智能组卷这一问题为研究核心, 提出基于改进和声搜索算法的英语考试智能组卷策略. 实验结果表明, 不同试卷期望时间下本文策略获取英语考试智能组卷可行解的概率都是0.99, 组卷精度较高; 迭代次数是300次时, 本文策略适应度最大值为0.70, 本文策略在求取英语考试智能组卷最优解时, 题库试题质量较好; 本文策略使用下, 计算机自动组卷后, 种群多样性在组卷前期都较高, 伴随迭代次数增多, 组卷后期本文策略种群多样性快速降低, 能够快速获取全局最优解.