近些年来, 从国家到地方, 各领域各企事业单位都投入大量人力、物力开展科研和产业建设, 在项目招标、申报、实施、验收等阶段, 都离不开遴选出相关专家进行评审. 随着国家经济发展和科技管理水平的提高, 各级单位每年立项的科技项目数量快速增加, 以自然基金委的科研项目为例, 仅在2019年国家自然科学基金项目申请集中接收期间, 国家自然科学基金委员会共计接收项目申请达到了240711项, 而国家电网总公司每年立项的科技项目也有300余项, 可见在短时间内对科技项目展开评审工作的任务量是极为繁重的.

随着项目管理流程的日益规范化, 如今在项目的立项论证、中期检查、成果验收、成果评价等多个环节都需要组织相关专家进行会审. 为了提高项目评审的效率, 目前各公司及单位普遍采用分组评审的策略, 但由于技术领域的日益细分和跨学科技术的广泛应用, 导致从业务和管理维度进行分组评审往往会使每个组的项目跨越较多的技术领域, 因此必须遴选出一组契合这些技术领域的专家才能实现对该组项目的有效评审.

目前传统专家遴选的方式普遍由人工作业完成, 在成千上万的专家库中检索出合适的专家组合十分具有挑战性. 由于候选专家排列组合的方案数巨大, 因此在有限时间内找出合适的专家团体变得十分困难, 亟需找到一种能合理为科技项目评审工作匹配出评审专家组合的解决方案, 以克服人工遴选专家方式所带来的种种弊端.

考虑到在分组项目评审过程中往往同时有多个项目和多位专家, 应为科技项目选出有限数量的评审专家, 使得这些专家组合成的评审团体可以较好地契合项目所涉及的各个相关领域. 本文首先将该问题建模为一个典型的组合优化问题, 通过将项目和专家映射到技术领域建立起科技项目和评审专家所对应于专业领域上的离散分布, 进而基于余弦相似度函数来量化评价该组科技项目和评审专家组之间的匹配度. 鉴于该类组合优化问题往往在多项式级时间复杂度上无法有效求解, 因此本文提出了基于贪心迭代搜索的GIS算法, 该算法主要采用了多轮迭代搜索最优部分解来组合形成全局最优解的策略以实现找出最优专家组合的目的. 本文最终将GIS算法分别在国家电网专家库及其历史立项科技项目真实数据集上进行了实验验证, 并研究了专家库大小、领域数量、项目数量等不同因素对算法的影响, 结果表明本文提出的GIS算法能在较短的时间内找到较优的评审专家组合方案.

1 相关工作

近些年来, 已有不少相关学者对专家推荐问题进行过深入的研究, 其中也不乏一些十分具有代表性的专家推荐方法, 目前的专家推荐方法大体可分为两类: 第一类是针对专家独立推荐的研究, 其主要思想是在推荐一位或多位专家时, 主要考虑将专家以独立个体的方式推荐得出, 即每位专家都与当前待评审项目存在一定程度上的强相关关系, 但不考虑所推荐专家形成组合后的整体情况; 第二类则是针对专家组合推荐的研究, 一般是在限定若干约束条件的情况下推荐出由多位专家组成的专家团体, 该专家团体实现了对于当前待评审项目能达到组合最优的评审效果, 但其中每位专家则不必精通每个待评审项目, 下面简要介绍在基于上述两种研究思路下当前已有的相关工作.

基于专家独立推荐的研究: 文献[1–5]均通过提出一种科技项目评审专家推荐系统模型, 该模型在挖掘文本信息的基础上运用关键词提取、特征权重计算等相关算法, 得到科技项目的多维度特征信息, 然后通过计算其与专家在词条上的相似度, 并综合专家参评项目经验及专家业务能力等因素, 最终使用基于内容推荐、协同过滤推荐以及专家评分加权因子相融合的混合推荐模型, 计算出每位专家的综合评分, 再根据设定的阈值以及推荐指数从高到低产生推荐专家名单实现了对科技专家的高效遴选; 文献[6–11]均通过提出了一种基于文本分类模型的方式来实现专家自动推荐的效果, 主要借助有监督或无监督的方式建立起专家知识模型来判断出评审专家的主要研究领域和评审项目的专业领域, 再将评审项目的专业领域与评审专家的研究领域按相似性自动匹配, 最终达到对评审专家精准推荐的目的; 文献[12–14]主要提出了一种基于主题模型的评审专家协同推荐方法, 即借助隐含狄利克雷分布模型构建主题特征空间, 并利用特征提取算法分别获得项目文档与专家文档的主题特征向量, 计算项目与专家主题特征向量的相关度并取项目相关度较髙的专家作为推荐结果.

基于专家组合推荐的研究: 文献[15–18]主要通过将项目与专家抽象为二分图网络模型, 由网络节点的关联性出发, 提出了一种基于相似度传播的复杂网络节点匹配方法, 通过借助图论中的KM算法、最大流匹配算法等方式实现节点间分组匹配的目的, 最终设计出项目与专家的多重匹配算法; 文献[19]提出一种基于语义挖掘的科技项目评审专家智能推荐方法, 为一个或多个项目自动推荐生成候选专家列表; 文献[20]提出一种适用于求解通用最大权完美匹配的智能优化方法, 该方法能自适应地从改进的离散粒子群策略以及模拟退火策略中选择适用于当前演化过程的有效策略, 并在保持种群稳定进化的同时促使种群快速收敛.

综上所述, 对于独立推荐专家的方式来说, 其主要关注点为挖掘专家与项目的知识信息, 并使用混合加权的方式来计算每个专家的综合得分, 最终基于该分数实现推荐. 但这种方式难以保证由多个高评分专家组合而成的团体也能契合实际项目需求, 具体来说, 当这些高评分专家均仅擅长于特定领域且彼此相似时, 那么此时的专家组合虽能满足每位专家最优, 但却无法保证该组合整体足够适合于当前项目的评审需求. 而基于专家组合推荐的方式则避免了这种情况的发生, 其实现方式主要是将项目和专家的关联关系抽象成二部图网络模型, 进而考虑使用如完美匹配、最大流匹配等图论算法实现专家遴选, 但这类算法常常由于具有较高的时间复杂度而难以将其应用到大规模数据集上. 为此基于上述考虑, 本文设计了一种抛弃传统二部图网络结构的专家组合推荐策略, 并最终将其运用到较大的数据集上实现了科技项目与评审专家的多重匹配.

2 问题定义

本文在考虑实际分组项目评审的情况下将该匹配问题进一步抽象描述如下:

当前共有 $n$ 个待审批科技项目, 用集合 $P = {\rm{\{ }}{P_1}, $ $ {P_2},\cdots,{P_i},\cdots,{P_n}{\rm{\} }}$ 来表示; 专家库中共有 $m$ 位专家, 用集合 $E = {\rm{\{ }}{E_1},{E_2},\cdots,{E_i},\cdots,{E_m}{\rm{\} }}$ 来表示; 项目集合 $P$ 与专家集合E共涉及 $l$ 个专业领域, 用集合 $F = {\rm{\{ }}{F_1},{F_2},\cdots,{F_i},\cdots, $ $ {F_l}{\rm{\} }}$ 来表示.

由于任意一个科技项目 ${P_i}$ 都与若干专业领域有一定的相关性, 这里记矩阵 ${W^{PF}}$ 来表示项目集合P与领域集合F的相关性矩阵, 其中 ${W^{PF}}$ 中的第 $i$ 行 $j$ 列的元素 ${w_{ij}}$ 表示科技项目 ${P_i}$ 与专业领域 ${F_j}$ 之间的相关度, 特别地, 当 ${w_{ij}}$ 的值为零时表示科技项目 ${P_i}$ 与专业领域 ${F_j}$ 之间没有关联关系.

${W^{PF}} = \left[ {\begin{array}{*{20}{c}} {{w_{11}}}&{{w_{12}}}&{...}&{{w_{1l}}} \\ {{w_{21}}}&{{w_{22}}}&{...}&{{w_{2l}}} \\ {\vdots}&{\vdots}&{\vdots}&{\vdots} \\ {{w_{n1}}}&{{w_{n2}}}&{...}&{{w_{nl}}} \end{array}} \right]$

(1)

同理, 因为任意一名候选专家 ${E_i}$ 都有其所擅长的研究领域, 所以仍可以得到矩阵 ${W^{EF}}$ 来表示专家集合E与领域集合F的相关性, 矩阵 ${W^{EF}}$ 表示如下:

${W^{EF}} = \left[ {\begin{array}{*{20}{c}} {{w_{11}}}&{{w_{12}}}&{...}&{{w_{1l}}} \\ {{w_{21}}}&{{w_{22}}}&{...}&{{w_{2l}}} \\ {\vdots}&{\vdots}&{\vdots}&{\vdots} \\ {{w_{m1}}}&{{w_{m2}}}&{...}&{{w_{ml}}} \end{array}} \right]$

(2)

假设每个科技项目 ${P_i}$ 都有其所关联的专业领域 ${F^{{P_i}}} = {\rm{\{ }}{F_{{x_1}}},{F_{{x_2}}},\cdots{\rm{\} }}$ , 对应于 ${W^{PF}}$ 中第 $i$ 行数据 $W_i^{PF} = $ $ \left( {{w_{i1}},{w_{i2}},\cdots,{w_{il}}} \right)$ , 那么对于当前待评审的项目集合 $P = $ $ {\rm{\{ }}{P_1},{P_2},\cdots,{P_i},\cdots,{P_n}{\rm{\} }}$ 来说, 该组项目所关联的专业领域 ${F^P}$ 可表示为 ${F^P} = \bigcup\limits_{i = 1}^n {{F^{{P_i}}}} $ , 对应到矩阵 ${W^{PF}}$ 即可得到能反映出项目集合所关联专业领域的离散分布, 记该离散分布为 $D(P)$ , 则其计算方式可定义为:

$D(P) = \sum\limits_{{P_i} \in P} {W_i^{PF} = } \left( {\sum\limits_{i = 1}^n {{w_{i1}},} \sum\limits_{i = 1}^n {{w_{i2}},\cdots,} \sum\limits_{i = 1}^n {{w_{il}}} } \right)$

(3)

同理, 若对已选出的 $k$ 位专家所组成的集合 ${E^{(k)}} = $ $ {\rm{\{ }}{E_{{x_1}}},{E_{{x_2}}},\cdots,{E_{{x_k}}}{\rm{\} }}$ 进行考虑, 其中每位专家 ${E_i}$ 所擅长的专业领域 ${F^{{E_i}}} = {\rm{\{ }}{F_{{x_1}}},{F_{{x_2}}},\cdots{\rm{\} }}$ , 那么同样可以找到能反映该专家团体 ${E^{(k)}}$ 主要研究方向的离散分布 $D({E^{(k)}})$ , 其计算方法如下所示:

$D({E^{(k)}}) = \sum\limits_{{E_x} \in {E^{(k)}}} {W_x^{EF} = } \left( {\sum\limits_{i = {x_1}}^{{x_k}} {{w_{i1}},} \sum\limits_{i = {x_1}}^{{x_k}} {{w_{i2}},\cdots,} \sum\limits_{i = {x_1}}^{{x_k}} {{w_{il}}} } \right)$

(4)

为了定义所遴选出的专家与待评审项目的匹配程度, 本文提出了一种评价函数 $S(P,{E^{(k)}})$ 来衡量当前选出的专家子集 ${E^{(k)}}$ 对项目集合P的匹配度. 该评价函数能够满足: 当项目集合 $P$ 所涉及专业领域与专家子集 ${E^{(k)}}$ 研究方向足够契合时, $S(P,{E^{(k)}})$ 始终能给出较高的评价, 反之则会给出较低的评价, 这样即可认为选定专家子集 ${E^{(k)}}$ 来评审该组科技项目是比较合适的.

因此可以借助前文所定义的离散分布 $D\left( {{E^{(k)}}} \right)$ 来表示专家子集 ${E^{(k)}}$ 的专业能力分布, $D(P)$ 用来表示项目集合P所涉及到的研究领域分布, 这样通过将两者信息映射到共同的专业领域维度上之后, 便可以进一步分析 $D\left( {{E^{(k)}}} \right)$ 与 $D(P)$ 两个离散分布间的匹配度. 显然当两个离散分布越“相似”时匹配度应当越高, 但考虑到用于衡量 $D\left( {{E^{(k)}}} \right)$ 和 $D(P)$ 两个离散分布相似性的方式有很多, 如基于欧氏距离、交叉熵、余弦相似度等函数, 然而对于描述了专家子集 ${E^{(k)}}$ 专业能力和项目集合 $P$ 研究领域的两个离散分布来说, $D\left( {{E^{(k)}}} \right)$ 和 $D(P)$ 之间的差异不应受到其具体数值大小的影响, 而应该侧重关注于两分布间整体趋势及结构上的相似性, 那么选用余弦相似度来定义此需求下两种离散分布的相似性是较为合适的. 因为根据余弦相似度函数的特性可知, 当把两个离散分布映射成高维空间上的向量后, 此时这两个向量的相似性将不再受到自身模值的影响, 而仅仅取决于其夹角的大小. 反映到离散分布上而言, 只有当两个分布的整体趋势及结构足够相似时, 即使两个分布之间具体数值可能相差若干倍, 但在余弦相似度函数的度量下, 仍会认为这两个离散分布是相似的, 这样也就限制了评价函数将侧重关注专家子集 ${E^{(k)}}$ 的所包含的主要研究领域与项目集合 $P$ 所涉及的研究方向的契合性, 以便能保证选定该专家团体来评审当前科技项目是完全合适的, 而若采用如欧氏距离、交叉熵等作为评价函数时则无法满足此项特性. 故综合上述考虑, 本文最终定义用于衡量当前选出的专家子集 ${E^{(k)}}$ 与项目集合 $P$ 之间匹配度的评价函数 $S\left( {P,{E^{(k)}}} \right)$ 为:

$S\left( {P,{E^{(k)}}} \right) = \cos \left[ {D(P),D\left( {{E^{(k)}}} \right)} \right] = \frac{{D(P) \cdot D\left( {{E^{(k)}}} \right)}}{{\left| {D(P)} \right|\left| {D\left( {{E^{(k)}}} \right)} \right|}}$

(5)

离散分布间结构相似性的度量方式如图1.

3 贪心迭代搜索算法

通过上一节的定义, 显然能计算出任意一组科技项目与评审专家集之间的匹配度大小, 那么 ${E^{(k)}}$ 便可以通过枚举E的所有 $k$ 元素子集并代入评价函数 $S\left( {P,{E^{(k)}}} \right)$ 中以找到最优的匹配方案. 但这样做其实在实际应用中是无法实现的, 因为通过穷举集集合E的所有 $k$ 元素子集 ${E^{(k)}}$ 其解的数量便高达 $C_m^k$ 种, 而现实评审状况则往往是专家库内候选评审专家数目 $m$ 是比较大的, 同时也需要选出一定数量的专家构成最终的评审专家团体, 那么上述方案将无法在可接受的时间范围内求解, 对此本节将介绍一种贪心迭代搜索算法(Greedy Iterative Search, GIS)以实现最优专家组合的高效遴选.

假设本组待审的科技项目集合记为 $P$ , 候选专家库内所有评审专家集合记为 $E$ , 最终需要在 $E$ 中匹配到一个包含 $k$ 名评审专家的组合 ${E^{(k)}}$ 来完成本期科技项目的评审工作. GIS算法的主要思想则是找出某个专家团体 ${E^{(k)}}$ 使得 $S\left( {P,{E^{(k)}}} \right)$ 最大, 在保证当前所选出的评审专家团体能达到较高匹配度的前提下, 算法每轮都会从未选择的专家库中挑选出若干名专家加入到当前的评审专家团体中, 并从中删去评价较低的专家组合方案, 下一轮将继续在本轮更新后的解集中继续加入更多的专家实现评审团体的扩充, 以此类推不断迭代直至产生出若干组评价较高且人数符合预期的评审专家组合, 最终GIS算法将在该集合中选出最优的专家团体 ${E^{(k)}}$ 来作为其所找出的评审专家团体.

由此定义GIS算法的具体实现步骤如算法1.

算法1. 贪心迭代搜索算法

1) 定义搜索参数 $\scriptstyle topK$ , 初始化当前解集集合 $\scriptstyle{G^0} = {\rm{\{ }}E_1^{(0)}{\rm{,}}E_2^{(0)}{\rm{,}}\cdots{\rm{,}}E_{topK}^{(0)}{\rm{\} }}$ ;

2) 遍历解集集合 $\scriptstyle G$ , 对每个专家团体 $\scriptstyle E_i^{(t)}$ 尝试加入专家 $\scriptstyle e,(e \notin E_i^{(t)})$ , 使得发生 $\scriptstyle E_i^{(t)} \to E_i^{(t + 1)}$ 的转变, 并对当前得到的所有新专家团体 $\scriptstyle E_i^{(t + 1)}$ 计算 $\scriptstyle S(P,E_i^{(t + 1)})$ , 并取其中评价最高的 $\scriptstyle topK$ 组加入到集合 $\scriptstyle{G^{t + 1}}$ 中;

3) 重复步骤2)使得所有专家团体 $\scriptstyle E_i^{(t)}$ 都求出相应的 $\scriptstyle E_i^{(t + 1)}$ 并将其全部加入集合 $\scriptstyle{G^{t + 1}}$ 中, 最终将得到 $\scriptstyle{G^{t + 1}} = \{ E_{11}^{(t + 1)},E_{12}^{(t + 1)},\cdots,E_{1topK}^{(t + 1)},\cdots,E_{topK1}^{(t + 1)}, $ $ \scriptstyle E_{topK2}^{(t + 1)},\cdots,E_{topKtopK}^{(t + 1)}\} $ ;

4) 根据 $\scriptstyle S(P,{E^{(t + 1)}})$ 的评价进一步削减集合 $\scriptstyle {G^{t + 1}}$ 的大小, 使该解集集合所包含可能解的数量仍为最优的 $\scriptstyle topK$ 组;

5) 至此由上述步骤已完成了一轮 $\scriptstyle{G^t} \to {G^{t + 1}}$ 的转变, 算法将继续迭代直到产生 $\scriptstyle{G^0} \to {G^1} \to \cdots \to {G^k}$ ;

6) 在集合 $\scriptstyle{G^k}$ 中找出能使 $\scriptstyle S(P,{E^{(k)}})$ 评价最高的专家团体 $\scriptstyle{E^{(k)}} = Max({G^k})$ , 此专家团体 $\scriptstyle{E^{(k)}}$ 即为GIS算法的最终输出.

分析GIS算法的执行流程可知, 该算法的主要运算成本集中在步骤2) ~ 5)上, 其中步骤2)将会迭代 ${{top}}K$ 次, 步骤3)和步骤4)迭代 $m$ 次, 步骤5)迭代 $k$ 次, 故GIS算法整体的平均复杂度为 ${\rm O}(topK \times m \times k)$ , 该复杂度远小于枚举法的时间复杂度(约为 ${\rm O}({m^k})$ ). 考虑到在实际的分组项目评审需求背景下, 一般 $m$ 的范围是 ${10^4}$ 量级, $k$ 的实际取值最大不会超过50, ${{top}}K$ 的可选区间亦一般不超过 ${10^2}$ 量级, 故本文提出的GIS算法在极端条件下的运算成本约为 ${10^7} \sim {10^8}$ 次, 这在目前的计算设备下普遍可以在分钟内完成, 已经具有一定的实际可行性.

4 实验分析

为了验证GIS算法的有效性, 本文使用了真实的电力行业科技项目评审数据集进行实验. 图2是GIS算法的搜索过程. 该数据集共包含有8364名电力行业资深专家, 涉及127个电力行业相关研究领域, 项目数据包含过去3年内国家电网总公司立项的科技项目共912项, 其中科技项目共分为90组, 每组包含的项目从5个到20个不等, 每个项目所涉及的专业领域也均在上述127个电力行业研究领域之内. 本节将通过使用该数据集来测试GIS算法对于解决专家遴选问题的表现, 并结合蛮力搜索算法、RandomSelect算法和GradualSubtract算法作为baseline构成对比实验以综合分析出GIS算法的有效性. 其中RandomSelect算法的基本思想是每次从专家库中随机挑选一名专家, 使得该专家加入当前专家团体后, 专家团体的评价分数能得到提升, 依此原则不断地挑选出指定数目的专家即可; GradualSubtract算法的主要思想则是每次都会从当前未被选择的专家中找出一名研究领域最多覆盖于当前项目的专家, 并将其加入到评审专家团体中, 然后从项目中删除这些技术领域, 接下来再重复地寻找下一位专家, 直至构建出最终的评审专家团体.

4.1 蛮力搜索算法的可行性

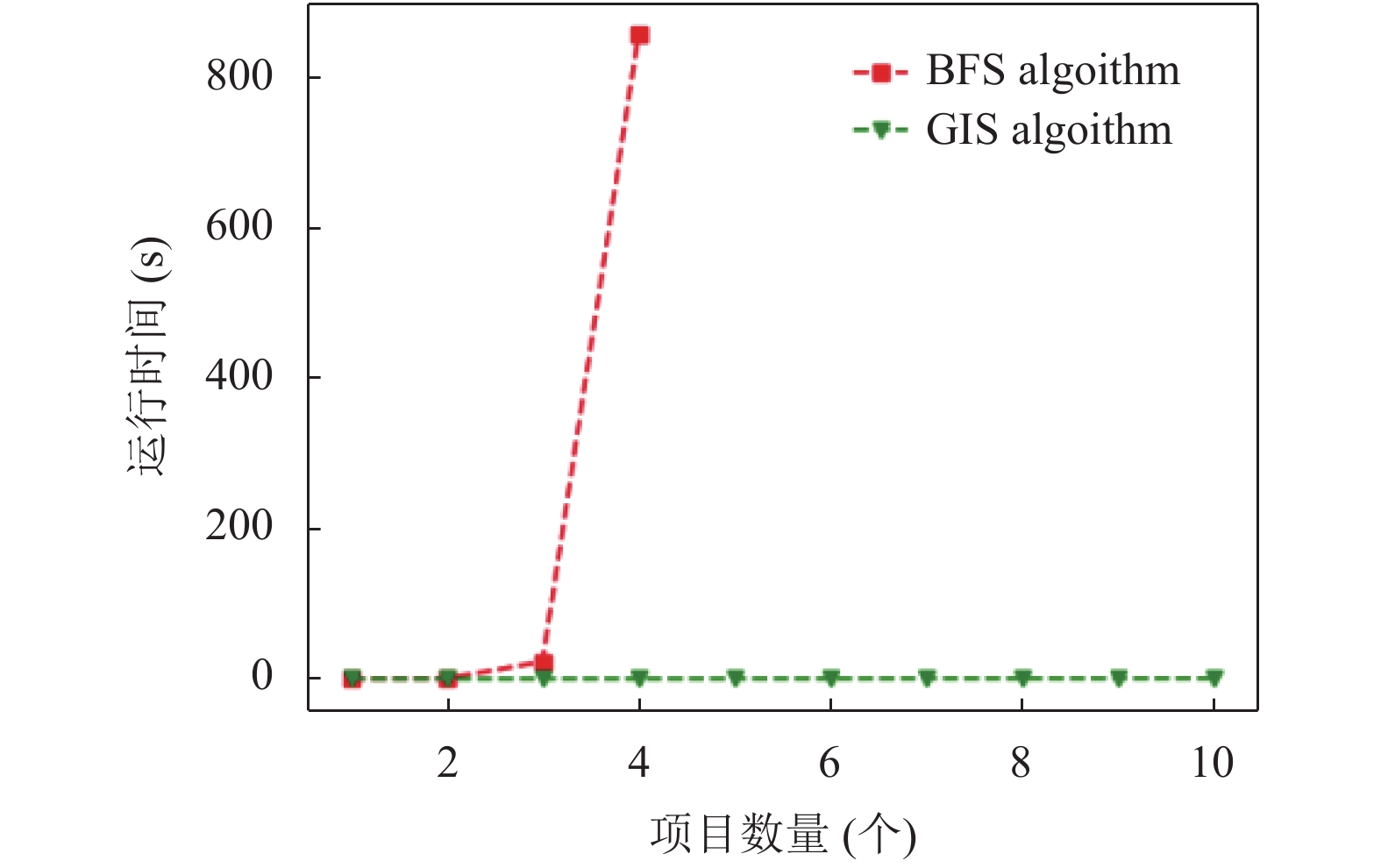
本节通过使用蛮力搜索算法(Brute Force Search, BFS)构成对比实验, 分析其与本文提出的GIS算法应用在真实场景下的可行性. 鉴于BFS算法在专家总量稍大时便会带来巨大的耗时, 所以本次实验仅选取了150位专家为全部候选专家, 测试其在面对包含1至10个科技项目的评审工作时, BFS算法和GIS算法所能达到的匹配度及耗时情况. 特别地, 由于分组评审工作中所需的评审专家数目与其所包含的科技项目数目一般为1:1配置, 所以本章所进行的实验也将默认采取这种设定.

图3和图4展示了在逐渐改变实验中每组评审工作中所包含的科技项目数量的情况下, BFS算法和GIS算法各自的耗时及匹配度表现. 不难发现当采用BFS算法后, 虽候选专家的总量仅有150个, 但面对包含4个科技项目的评审需求时, 便难以在可接受的时间尺度上找出一种合适的评审专家组合方案; 相比之下, 本文提出的GIS算法则能保证在尽量少的耗时下达到与BFS算法一致的匹配度表现, 可见该算法有处理较大数据集的潜力, 能应用于现实情景下的实际需求.

4.2 专家库大小的影响

本节将测试在逐渐改变专家库大小的情况下, 分析GIS算法对于包含20个科技项目的评审工作需求时的表现情况, 图5和图6记录了实验过程中RandomSelect算法、GradualSubtract算法和GIS算法的匹配度及耗时表现. 通过对比不难分析出当专家总量逐渐增大时, GIS算法所找出的专家组合方案的匹配度会逐渐升高, 直至专家总量达到2000左右时趋于稳定; 相比之下, RandomSelect算法与GradualSubtract算法的匹配度表现则较差, 其中RandomSelect算法的匹配度一直处于0.5到0.6的范围内上下波动, 而GradualSubtract算法的匹配度虽在不断升高, 但其提升速度及稳定上限相比于GIS算法仍有一定差距.

考虑算法的运行时间而言, 当K值为30时GIS算法的耗时最多, 而将K值下调至5后GIS算法的整体耗时便能显著下降. 值得注意的是, 虽然此时GIS算法的整体耗时仍略多于RandomSelect算法和GradualSubtract算法, 但不难发现其匹配度表现已经有了较大幅度的提升.

4.3 领域数量的影响

本节将通过调整每组评审工作中包含的20个科技项目所涉及专业领域的数目, 探究领域数量对于本文所提出的GIS算法的影响, 如图7和图8. 由实验中匹配度曲线和耗时曲线不难看出, 当逐渐增大项目所涉及的领域数量后, RandomSelect算法、GradualSubtract算法和GIS算法的耗时曲线基本处于稳定状态, 虽个别情况下有小范围的波动, 但总体上这3种算法的耗时表现均不会受领域数量变化的影响.

同时根据匹配度曲线亦可以发现, RandomSelect算法的匹配度表现会随着领域数量的增多而出现明显下降, GradualSubtract算法的表现则相对稳定, 其匹配度曲线在发展趋势上并未出现明显变化. 相比之下, 本文提出的GIS算法的表现最好, 其匹配度曲线始终能保持在较高位且整个过程中十分稳定, 所以本实验证实了通过改变领域数量不会对GIS算法的匹配度表现产生根本性影响.

4.4 项目数量的影响

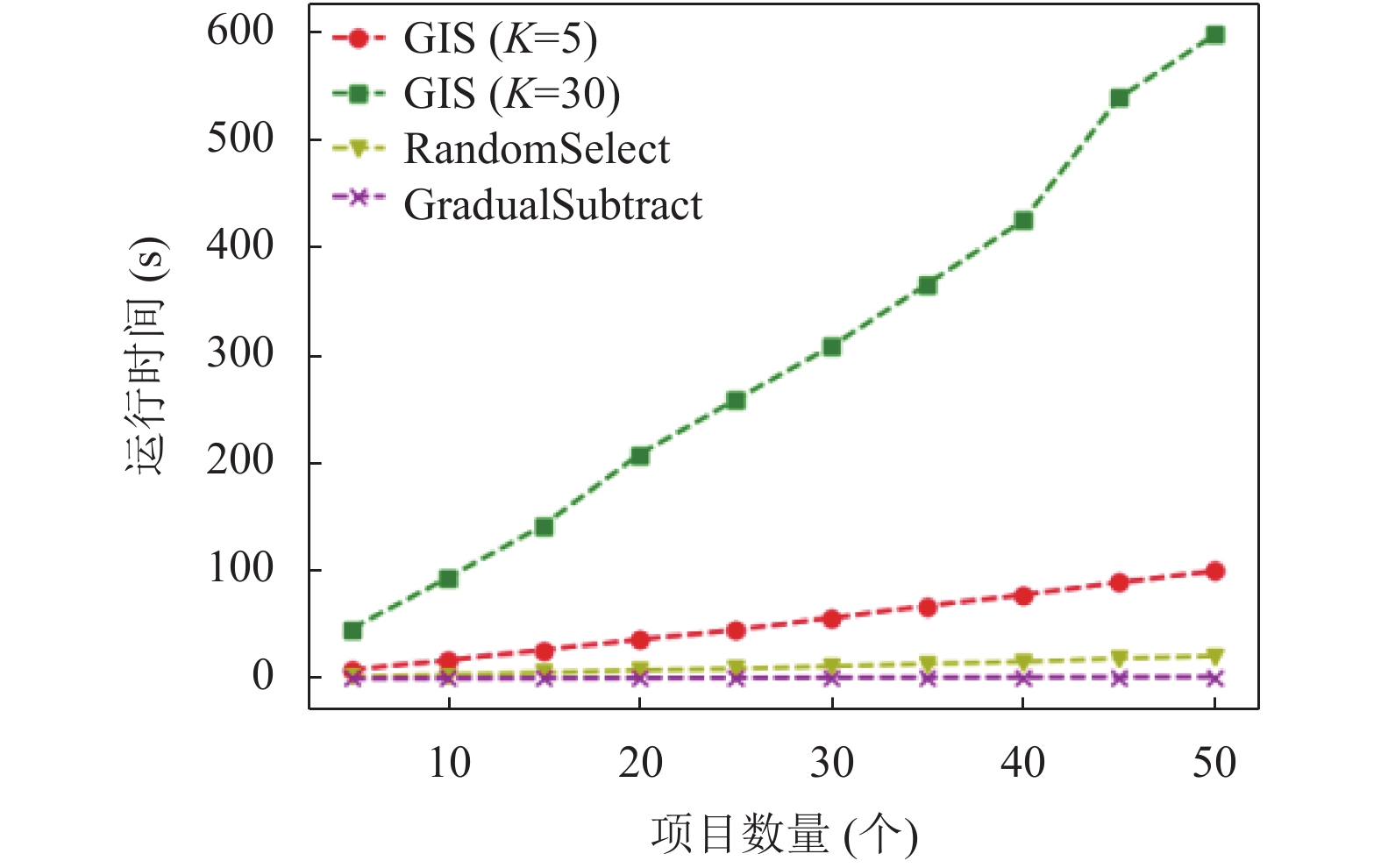
本节最后将通过改变每期评审工作中所包含科技项目的数量测试其对GIS算法的影响, 图9和图10记录了实验过程中在逐渐增大项目数量后RandomSelect算法、GradualSubtract算法和GIS算法的表现. 不难看出当项目数量逐渐增大时, RandomSelect算法和GradualSubtract算法的耗时相对较少, 而K值为5的GIS算法耗时则略多, 且随着科技项目数量的增加, K值设置的越大GIS算法的耗时增长越为迅速.

同样对比这3种算法的匹配度曲线可知, GIS算法相比于RandomSelect算法和GradualSubtract算法的表现更好, 且增大 $K$ 值后GIS算法的表现仍会有小幅提升. 其中GradualSubtract算法的匹配度表现最高时可达到0.88的匹配度, 而RandomSelect算法最高时仅达到0.66的匹配度, 且其整体表现较不稳定; 相比之下GIS算法的匹配度表现则更加稳定且优异, 其匹配度始终能保持在0.95左右.

5 结束语

本文提出了在分组项目评审的背景下求解最优评审专家组合的GIS算法, 该算法主要通过约束贪心算法的搜索空间, 多轮迭代后找出契合本期项目评审需求的专家团体. 通过借助电力行业数据集对该分组项目评审专家遴选问题进行实验分析, 结果表明本文提出的GIS算法在计算耗时和计算效果上均有较好的表现, 可以将其应用到实际的科技项目评审工作之中.