我国有着辽阔的海岸线和大量岛屿, 虽然我国很多沿海城市没有处在板块交界处, 发生海啸的可能性不像邻国日本那样多. 但近几年, 较多的海底大地震给我国台湾岛和福建沿海城市造成海啸的可能性变大. 针对可能发生海啸的安全隐患问题, 利用一定的分析评估方法是防灾减灾的重要手段之一.
目前在实践层面上, 广泛使用的海啸分析是基于浅水长波理论[1]的数值分析, 该理论中假设水粒子的垂直加速度非常小, 取垂直方向上流速的均值. 这种分析方法对二维现象进行了模拟, 可用于理解从地震中心至沿海城市广阔区域上的海啸传播. 然而, 该方法难以确定3D属性在其中占主导地位的局部水流的自由表面形状[2]. 一般情况下, 海啸预测的内容是海啸到达地面后, 随时间发展, 海水覆盖的区域变化情况. 此外, 由于水波的三维性会造成的影响, 建筑物附近的水流预测也是预测内容之一, 但前者通常为预测的主要内容.
GIS数据以其在时空数据的存储表达分析等方面的优势, 使得在多种3D仿真和可视化领域得到广泛关注, 如溃坝洪水演进[3]、洪水淹没分析[4]等. 传统GIS方法大多采用数字高程模型(Digital Elevation Model, DEM)[5], 利用有源淹没或者无源淹没进行分析, 其缺点是忽略了物理学和动力学的因素, 时效性和可靠性较弱.
在3D流动分析中, 当水波发生显著变化时, 网格的数值分析方法[6]也经常被使用, 如有限差分法和有限元法[7]等. 在众多理论分析方法中, 光滑粒子流体动力学(Smoothed Particle Hydrodynamics, SPH)[8]逐渐得到认可. SPH是一种无网格的拉格朗日粒子法, 其基本思想是将连续的流体用相互作用的粒子组来描述, 各粒子上承载各种物理量, 包括质量、速度、加速度等. 通过求解粒子组的动力学方程和跟踪每个粒子的运动轨迹, 求得整个系统的力学特征[8]. SPH在海啸3D仿真[9]、洪水灾难评估[3,10]等方面得到了应用, 验证了SPH具有一定的可行性和准确性. 也有研究者将SPH扩展到不可压缩的光滑粒子流体动力学(Incompressible Smoothed Particle Hydrodynamics, ISPH)[11].
本文在SPH方法的基础上, 对边界问题和缓解不可压缩问题进行描述和解决, 建立能够对海啸爆发进行有效分析的工具. 提出了一系列的预处理程序和地理分析模型. 该模型能够通过从一个地理信息系统(GIS)中, 得到的3D位置信息(SHP)和数字高程模型(DEM)来展示地形、海拔和建筑物的外部形态.
2 提出的分析方法 2.1 SPH方法的基本方程SPH方法的基本概念是将位于空间点x和时间t的函数
| $\phi ({\bf{x}},t) \approx \int_V {W(|{\bf{x}} - {\bf{y}}|,h)} \phi ({\bf{y}},t)d {\bf{y}}$ | (1) |
式中, W为核函数, 即一种加权函数. 在SPH方法中, 一般将光滑长度在h内, 具有非零正值, 且满足统一条件的紧支撑函数作为一个近似. 基于离散化, 使用分布在空间中的粒子
| $ < {\phi _{ i}} > ( \approx \phi ({{\bf{x}}_i},t)): = \sum\limits_j {\frac{{{m_j}}}{{{\rho _j}}}} ({r_{ij}},h)\phi ({{\bf{x}}_j},t)$ | (2) |
式中, 下标i和j表示粒子数量,
为求解不可压缩的流体问题, 应该在满足质量守恒和动量守恒定律的前提下, 得出两个自变量, 即流速u和压力p. 控制方程的拉格朗日形式定义如下:
| $\frac{{D\rho }}{{Dt}} + \rho \nabla \cdot {\bf{u}} = 0$ | (3) |
| $\frac{{D{\bf{u}}}}{{Dt}} = \frac{1}{\rho }\nabla \rho + v{\nabla ^2}{\bf{u}} + {\bf{g}}$ | (4) |
式中, v为动力粘性系数, g为重力加速度.
假设水的密度是恒定的, 基于这一假设, 可以将质量守恒定律(式(3))改写为:
| $\nabla \cdot {\bf{u}} = 0$ | (5) |
将式(4)和式(5)应用到粒子i, 得到:
| $\frac{{D{{\bf{u}}_i}}}{{Dt}} \approx - \frac{1}{{{\rho _{ i}}}} < \nabla {p_{ i}} > + v < {\nabla ^2}{{\bf{u}}_i} > + {{\bf{g}}_i}$ | (6) |
| $ < \nabla \cdot {\bf{u}} > \approx 0$ | (7) |
ISPH方法[11], 使用投影法对运动方程的速度场和压力场进行分离, 以达到对压力场的隐式计算, 和速度场的显式计算. 另外, 使用投影法, 通过定义一个暂定状态, 可以对速度场和压力场进行分离.
下面将投影法应用到SPH方法中, 从n至n+1对变量进行更新. 首先, 对式(4)中的时间导数项进行前向差分近似, 并将中间速度u定义在一个中间状态, 以对速度进行分离:
| $\frac{{D{\bf{u}}}}{{Dt}} = \frac{{{{\bf{u}}^{n + 1}} - {{\bf{u}}^n}}}{{\Delta t}} = \frac{{{{\bf{u}}^{n + 1}} - {{\bf{u}}^ * }}}{{\Delta t}} + \frac{{{{\bf{u}}^ * } - {{\bf{u}}^n}}}{{\Delta t}}$ | (8) |
在分离后的加速度分量之间, 计算中间速度u如下:
| $\begin{split} \frac{{{\bf{u}}_i^ * - {\bf{u}}_i^n}}{{Dt}} =& v < {\nabla ^2}{\bf{u}}_i^n > + {{\bf{g}}_i} \\ \to& ({\rm{predictor}}){\bf{u}}_i^ * = {\bf{u}}_i^n + \Delta t\left( {v < {\nabla ^2}{\bf{u}}_i^n > {{\bf{g}}_i}} \right) \\ \end{split} $ | (9) |
这里假定式(9)右边的第一项和第二项分别对应于式(4)的压力梯度项和其他项. 然后, 对从中间状态至下一个时间步的速度进行更新:
| $\begin{split} \frac{{{\bf{u}}_i^{n + 1} - {\bf{u}}_i^ * }}{{\Delta t}} =& - \frac{1}{\rho } < \nabla p_i^{n + 1} > \\ \to& ({\rm{corrector}}){\bf{u}}_{}^{n + 1} = {\bf{u}}_{}^ * + \Delta {\bf{u}}_{}^ * \\ \end{split} $ | (10) |
| $\Delta {\bf{u}}_{}^ * = - \Delta t\left( {\frac{1}{\rho } < \nabla p_i^{n + 1} > } \right)$ | (11) |
如上所述, 通过实施两个单独过程, 以对速度的状态进行更新. 而压力是通过求解压力Poisson公式获得:
| $\begin{gathered} < {\nabla ^2}p_i^{n + 1} > = - \frac{{{\rho ^0}}}{{\Delta t}} < \nabla \cdot \Delta {\bf{u}}_i^ * > = \frac{{{\rho ^0}}}{{\Delta t}} < \nabla \cdot {\bf{u}}_i^ * > \\ \end{gathered} $ | (12) |
为了缓解不可压缩条件, 作如下定义:
| $ < {\nabla ^2}p_i^{n + 1} > \approx \frac{{{\rho ^0}}}{{\Delta t}} < \nabla \cdot {\bf{u}}_i^ * > + \alpha \frac{{\rho _{ i}^0 - < \rho _{ i}^n > }}{{\Delta {t^2}}}$ | (13) |
在SPH方法中, 从粒子的分布中对密度进行数值计算. 在分析过程过程中很难始终满足恒定密度条件, 因为仅在邻近粒子为固定数量且粒子保持完全的均匀分布时, 密度才是恒定的. 因此, 有必要采用一个折中方案, 即: 密度长期没有变化, 但允许密度在瞬间存在一定程度的误差.
式(13)给出的压力Poisson方程完全服从无散度条件下的模型(松弛参数为零). 此外, 当瞬间密度与初始密度吻合(或密度小到可以忽略不计), 则压力Poisson方程和模型可被视为相同, 因为压力Poisson方程源项的第2项可以忽略不计. 根据该公式, 通过密度差项逐步消去分析过程中产生的累积误差, 使得即使长期计算, 密度也几乎保持恒定, 从而得到了较好的体积守恒方案.
2.4 利用虚拟标记进行边界处理在粒子法的边界处理中, 一般会假设一个分析模型, 该模型的墙壁边界基本符合物理边界. 然而, 对于曲线或梯度边界, 很难得到粒子在边界内部的均匀分布. 因此, 在粒子模型的实际开发中, 粒子通常被放置在格子(将CAD数据划分为网格结构)的中心点或交点处. 通过这一简单预处理, 实现了粒子在一个区域的均匀分布; 然而, 粒子在边界的分布呈阶梯状, 这样的分布不同于实际物理边界中的平滑分布. 由此导致边界附近的流动不自然.
针对该问题, 本文处理的方法是: 将虚拟标记与墙壁粒子对称地放置在墙壁边界上. 虽然虚拟标记与SPH方法的计算没有直接关系, 但其测量点被用于对墙壁粒子施加适当的边界条件. 这里, 为满足边界表面上的滑移条件, 假设墙壁粒子的速度为
| ${{\bf{v}}_{\bf{w}}} = {\bf{M}}{{\bf{v}}_{\bf{v}}}$ | (14) |
式中, M为二阶张量, 其利用一个内向法线向量
| ${M_{ij}} = {\delta _{ij}} - 2{n_i}{n_j}$ | (15) |
为满足非滑移条件, 计算与虚拟标记流速
| ${{\bf{v}}_{\bf{w}}'} = R{{\bf{v}}_{\bf{v}}}, {R_{ij}} = - {\delta _{ij}}$ | (16) |
接下来, 确定虚拟标记的压力, 使之满足墙壁表面不均匀压力的Neumann条件[12]即可:
| $\partial p/\partial {\bf{n}} = \rho (v{\nabla ^2}{\bf{v}} + {\bf{g}}) \cdot {\bf{n}}$ | (17) |
式中, n为墙壁的内向法线向量.
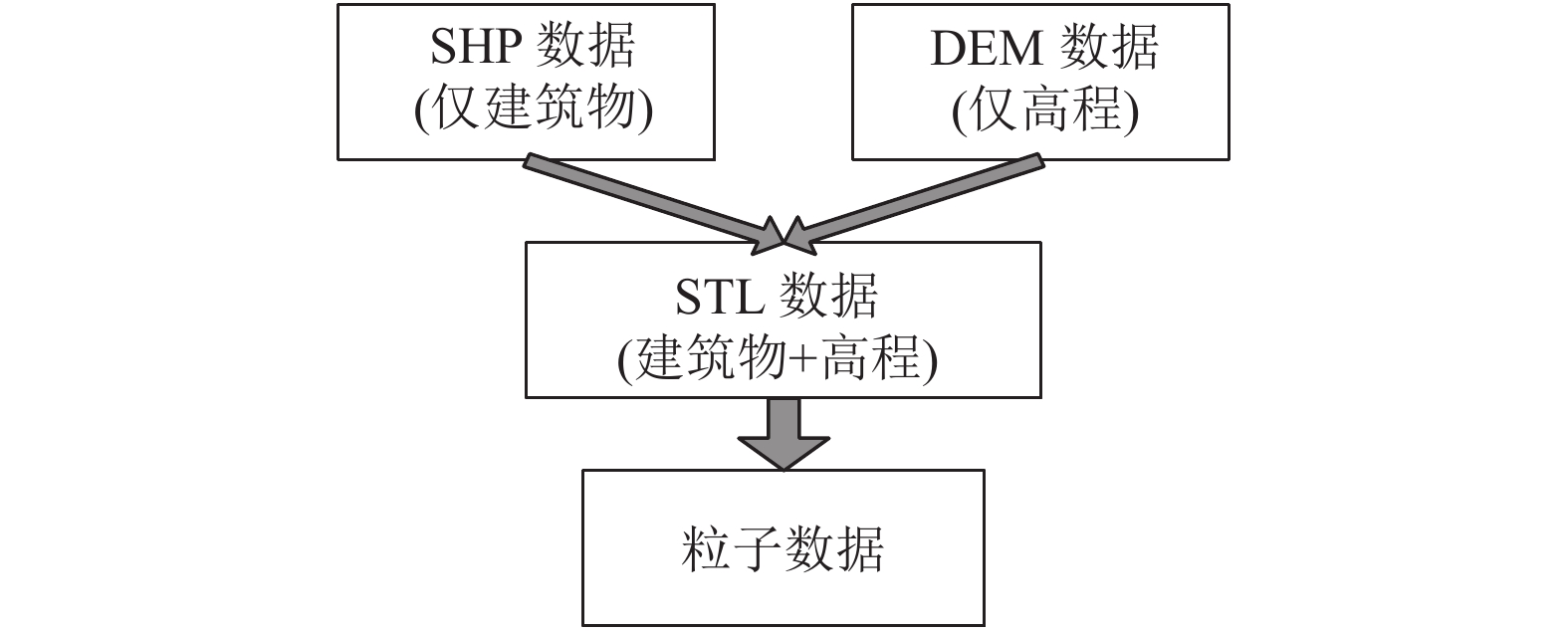
3 分析模型的开发在对海啸爆发进行建模时需要考虑到作为主要障碍物的建筑物. 众所周知, 3D分析的准确度很大程度上取决于分析模型的可靠性. 为了尽可能地将模型海拔高度和建筑物形态与实际的地理位置相匹配, 本文建立了一个利用GIS数据进行粒子分析模型的程序. 根据海拔上的DEM数据和建筑物上的SHP数据, 开发出粒子分析模型. DEM数据是通过航测得到的高程数据, 并以等间隔的网格形式保存. DEM数据剔除建筑物高度数据, 给出了地表高程. 由此, DEM数据一般用作高程数据, 而SHP数据(GIS地理空间数据文件的一种格式)一般用于定义建筑物的几何形状. 在SHP数据中, 每个建筑物的轮廓被定义为2D数据, 其中还包括了建筑物的高度信息. 当使用通用3D CAD数据定义地表和建筑物的轮廓时, 可以使用粒子分析的通用预处理程序(例如Meshman服务)将该3D CAD数据转换为粒子模型数据. 图1给出了本文粒子模型的开发流程.
|
图 1 粒子模型的开发流程 |
下面将解释使用上述两类GIS数据, 将地表轮廓定义为STL数据(类似于三角面片的一种3D CAD格式), 以及STL数据转换为粒子数据的一系列程序. 遵循的基本流程是: 从DEM数据中估计出每个建筑物位置的高程数据, 并使用SHP数据基于建筑物的平面轮廓对建筑物的高度进行扫描, 从而将高程数据转换为3D CAD数据. 由于地表通常包含斜坡; 因此, 在一个建筑物的底部和地表之间可能会产生间隙. 如果在粒子模型中不进行任何修正, 则粒子可能会进入该间隙. 因此, 当制备建筑物的CAD数据时, 将建筑物的底部降低一个恒定的量(5 m), 如图2所示.

|
图 2 降低STL数据的建筑物底部 |
本文使用的粒子分析预处理程序能够为CAD数据中定义的多个表面, 独立地生成粒子. 并在粒子的位置与另一个粒子的位置发生重叠时, 按照优先次序移除重复粒子, 开发出具有均匀粒子分布的分析模型. 由此, 将定义地表的STL数据和定义建筑物的数据, 分别存储在单独的文件中. 接着, 如图3所示对建筑物和地面粒子进行制备, 通过将地面粒子设为高优先级以使得建筑物粒子和地面粒子在与地表相对应的区域中发生重叠时, 自动移除建筑物粒子.

|
图 3 地面粒子 |
4 分析与评价
下面将基于前文解释的方法, 开发一个分析模型, 并使用SPH方法对一个沿海城市海啸爆发进行分析.
4.1 分析条件直径为2米粒子的分析模型如图4所示. 在该分析中, 假设海啸的波形会急剧上升. 通过放置在目标区域下的水流对河流进行模拟. 假设河流的平均海拔低于海平面4 m, 该河底部上为高度8 m的水体.

|
图 4 分析模型的示意图 |
基于长波理论, 该河的流速公式为
| 表 1 分析条件 |
4.2 结果评价
在海啸流入开始后60 s (时间步为12 000)时, 3个案例的结果如图5(a)所示. 海啸粒子没有渗透入建筑物, 这说明了已成功开发出分析模型, 在建筑物和地面之间没有间隙. 在对3个案例的分析结果进行比较时, 本文发现被淹没的陆地面积随空间分辨率的增大而增加. 在对粒子直径1 m和2 m, 以及2 m和4 m案例被淹没面积之间的差异进行比较时, 前者间的差异要小于后者间的差异, 这意味着数值分析的结果随空间分辨率的增加而收敛. 图5(b)给出了图5(a)中框内区域的放大视图, 该区域中差别较为明显. 图5(b)中定义的点A、B、C处测量到水位升高情况. 在不同分辨率模型之间的比较中, 海啸到达时间和水位升高历史表现出相似趋势.
由图5, 在使用直径为1 m的粒子与使用直径为2 m的粒子案例中观察到了相同的趋势; 然而, 使用直径为2 m粒子的案例中观察到的趋势, 则未出现在粒子直径为4 m的案例中. 即使使用Meshman从相同的STL数据中生成粒子, 但在不同分辨率下, 地形表示和建筑物形状均会发生变化. 特别是当使用低分辨率时, 其未能展示建筑物之间的小路, 从而导致海啸爆发中出现阻塞物. 举例来说, 单车道的平均道路宽度为3.5 m, 而使用直径为4 m的粒子时, 分析模型不会展示出此类道路. 此外, 低分辨率将导致地面梯度的再现性较低, 从而使分析准确度较低.

|
图 5 海啸爆发分析示意图 |
图5中没有展现的是, 在使用直径1 m的粒子时, 整个东侧的海拔大约比西部海拔低1 m. 然而, 在使用直径为2 m或4 m的粒子时, 均未观察到这一趋势. 因此, 使用1 m粒子时, 可能会造成高程重现性的下降. 综上, 应该采用粒子直径为2 m的空间分辨率对沿海城市地区的海啸爆发进行建模, 该分辨率能够重现主要道路, 从而实现较高的准确度. 图6给出了海啸开始流入后150 s (时间步30 000处)时的被淹没区域.

|
图 6 海啸流入150 s后被淹没的区域 |
4.3 照片级的可视化
在传统的可视化方法中, 粒子一般被表示为原始形状. 使用这一可视化方法, 可以对计数的类型进行切换 但照片缺乏真实感.
本文使用建筑领域可视化软件Lumion开发了3D动画. Lumion提供了使用视差效果进行3D动画创建的功能, 支持创造带有真实感的3D动画, 还可以导入通用CAD数据, 可加入与景物、日照条件和阴影相关的数据. 因此, 只有通过分析模型中虚拟城市的CAD数据和海啸的CAD数据, 才能实现3D可视化. 此外, 在对海啸的表面进行定义后, 将建筑物的真实图像加入建筑数据, 并将水流纹理加入海啸数据中, 以产生真实感, 进行可视化的一系列程序如图7所示. 可视化的示例如图8所示.

|
图 7 可视化方法的程序 |

|
图 8 3D可视化照片的示例 |
4.4 与网格法的比较分析
网格法在诸多分析中经常使用. 在3D流动分析中, 当水波的波形变化显著变化时, 使用网格的数值分析方法(例如限差分法和有限元法等)会变得非常复杂. 在发生较大形变的过程中, 自由表面形状可能会发生显著变化, 会发展成不连续的表面, 网格也可能会崩溃. 与之相比, 没有使用网格的粒子法在处理此类场景时具有一定优势, 其可以使用一个简单的算法对复杂的自由表面变化进行分析. 因此, 粒子法能够有效表达当爆发到陆地上以及在建筑物周围流动, 水波发生复杂变化的3D现象. 另外, 考虑复杂目标(包括建筑物)的分析模型时, 粒子法的开发成本更低, 因为在粒子法仅需要考虑粒子在目标区域中的放置问题.
在海啸爆发的3D分析中, 无论使用的是网格方法还是粒子方法, 都应该事先确定空间分辨率(粒子法背景下为平均粒子距离)和分析准确度之间的关系, 特别是在3D分析中, 由于极高的分析成本, 应该尽可能降低分辨率.
5 结论和展望本文利用3D粒子法(SPH方法)开发出沿海城市地区的海啸爆发分析模型. 基于粒子法的空间分辨率和被淹没区域之间的关系, 得出了进行海啸爆发分析所需的最小粒子距离. 然后创建了具有真实感的3D动画快照. 3D仿真验证了所提方法的有效性. 通过比较在相同条件下进行的分析结果, 确定了收敛解所需的最低空间分辨率.
未来, 本文将着力开发能够对特定区域进行缩放的多步骤分析技术, 对不同区域采用不同的粒子距离. 因此, 不同方法的结合和缩放分析将是本文后续研究方向.
| [1] |
安超. 利用流固耦合模型研究影响海啸波产生、传播和骤升高度的因素[硕士学位论文]. 北京: 北京大学, 2010.
|
| [2] |
张景新. 复杂地形下带自由表面水流的分离涡模拟. 计算物理, 2015, 32(5): 561-571. DOI:10.3969/j.issn.1001-246X.2015.05.008 |
| [3] |
李忠, 唐新明, 李少达, 等. 溃坝洪水演进的光滑粒子流体动力学分析. 测绘科学, 2016, 41(10): 115-119, 148. |
| [4] |
丁雨淋, 杜志强, 朱庆, 等. 洪水淹没分析中的自适应逐点水位修正算法. 测绘学报, 2013, 42(4): 546-553. |
| [5] |
孙臣良, 张峰. 基于ArcGIS Engine的大平矿库区GIS开发技术研究. 计算机应用与软件, 2013, 30(4): 296-298, 322. DOI:10.3969/j.issn.1000-386x.2013.04.085 |
| [6] |
Nießner M, Zollhöfer M, Izadi S, et al. Real-time 3D reconstruction at scale using voxel hashing. ACM Transactions on Graphics, 2013, 32(6): 169-178. |
| [7] |
谢珊珊. 非线性对流扩散方程LDG方法的误差估计[硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2016.
|
| [8] |
刘桂荣. 光滑粒子流体动力学. 长沙: 湖南大学出版社, 2005.
|
| [9] |
O-Tani H, Chen J, Hori M. Automatic combination of the 3D shapes and the attributes of buildings in different GIS data. Journal of Japan Society of Civil Engineers, 2014, 70(2): I_631-I_639. |
| [10] |
Pourabdian M, Qate M, Javareshkian A, et al. Simulation of 2-D dam break using improved incompressible smoothed particle hydrodynamics based on projection method. Applied Mechanics and Materials, 2013, 390: 81-85. DOI:10.4028/www.scientific.net/AMM.390.81 |
| [11] |
Asai M, Aly AM, Sonoda Y, et al. A stabilized incompressible SPH method by relaxing the density invariance condition. Journal of Applied Mathematics, 2012, 45(11): 2607-2645. |
| [12] |
李红艳, 周盛凡. Neumann边界条件下强阻尼波动方程的-维全局吸引子. 数学学报, 2006, 49(6): 1381-1386. DOI:10.3321/j.issn:0583-1431.2006.06.027 |
 2021, Vol. 30
2021, Vol. 30


