目前, 将海量数据存储在分布式存储系统中的不同存储节点上的数据存储方式已在实际系统中得到了广泛应用, 如Google文件系统[1]、Hadoop文件系统等. 为确保分布式存储系统中数据的可用性和可靠性, 通常采用诸如复制策略[2]或纠删码策略[3, 4]的数据冗余策略. 以复制策略中的三副本复制为例, 三副本复制需要存储大量副本数据以确保系统较高的可靠性, 存储代价过高; 纠删码策略的提出使得修复造成的存储开销显著降低, 但其过大的修复带宽开销也成为了限制它的瓶颈.
2007年, Dimakis等人指出存储开销和修复带宽开销之间存在某种平衡, 平衡曲线上的点可通过再生码来实现[5]. 再生码基于网络编码的概念, 其故障节点可通过连接一定数目的存活节点完成修复, 相比于纠删码降低了修复带宽开销. 目前再生码的研究主要集中在最小存储再生码和最小带宽再生码[6].
El Rouayheb和Ramchandran为进一步降低修复过程中的运算复杂和带宽开销, 提出了一种基于最小带宽再生点的精确修复编码-部分重复(Fractional Repetition, FR)码[7]. 部分重复码结合再生码和复制策略的优点, 有效减少了修复带宽开销和磁盘I/O开销[8], 并实现精确的无编码修复.
目前, FR码主要采用分组设计[9]、可分解设计[10, 11]等方法进行构造. 朱兵等人基于分组设计提出一种重复度异构的FR码的构造[12], 使得常用数据的备份更加充分, 且参数选取范围较大, 但同时也造成了较大的存储开销; Natalia Silberstein和Tuvi Etzion等人基于组合设计和正则图, 提出了一种达到最大码率的FR码的构造方法[13], 但其重复度受FR码结构的约束, 不能适用于任意参数; Harout Aydinian和Holger Boche等人则基于部分有序集构造了一种普遍好的FR码[14], 这种构造方法虽然简便, 但其重复度却也十分受限. 为此, 本文基于Harary图生成树构造出了一种新型的部分重复(Fractional Repetition based on Spanning trees of Harary graph, FRSH)码, 可以在很大范围内选择构造参数和数据块的重复度, 还能修复多个故障节点. 通过调整Harary图的构造参数, 可以构造出不同重复度的FR码. 相比现有的FR码, 采用Harary图生成树设计FR码更加简洁直观. 相较于RS码和SRC[15], FRSH码在修复带宽开销、修复复杂度以及修复局部性等方面得到了更低的开销, 且改善了修复效率, 并将故障节点修复时间缩短.
1 预备知识 1.1 Harary图的基础知识Harary图是一种正则图, 定义为
(1) k是偶数
设
(2) k是奇数, m是偶数
设
(3) k是奇数, m是奇数
设
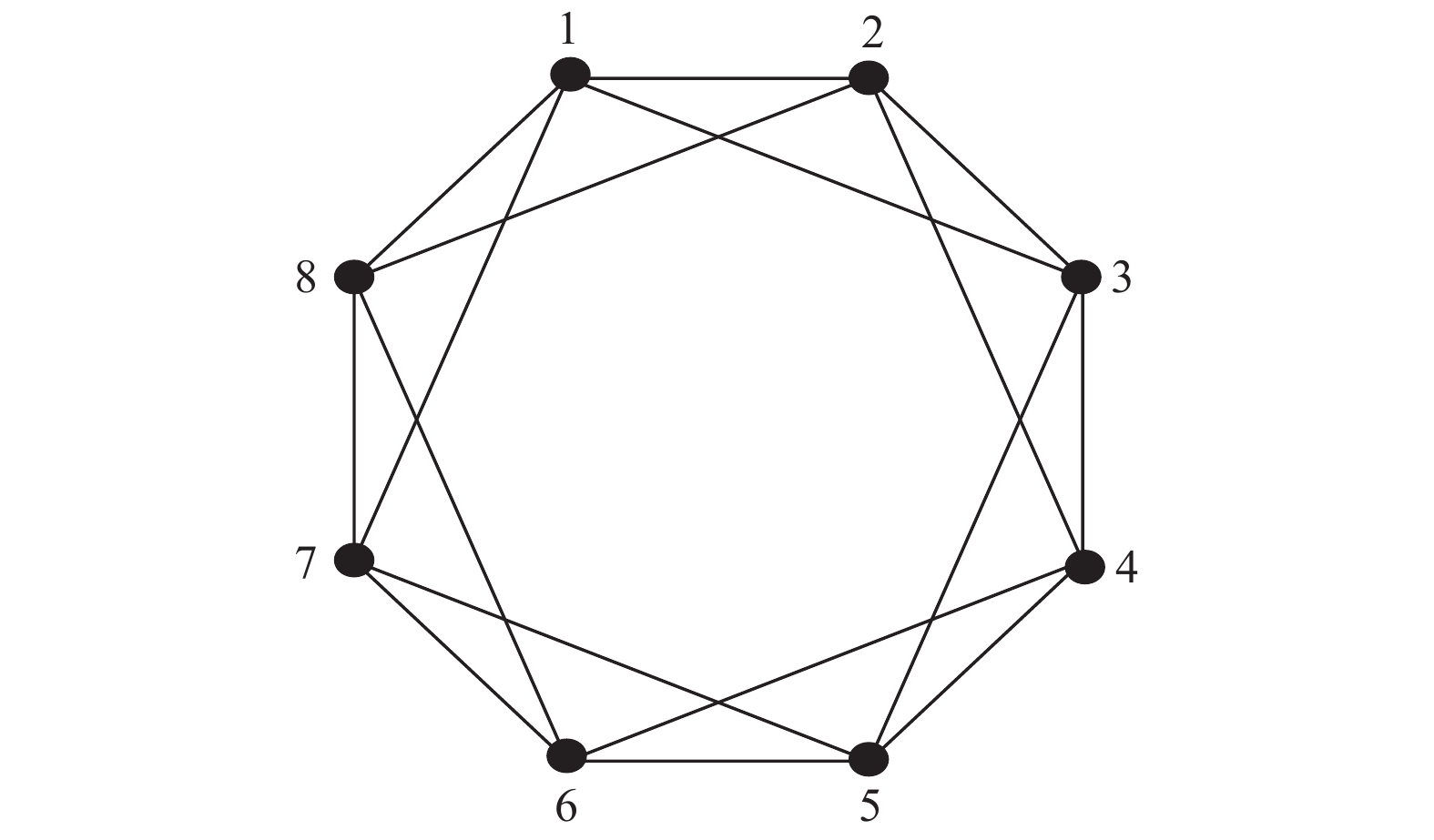
图1所示是构造的k=4, m=8的Harary图
无圈图是指不包含圈的图, 连通的无圈图定义为树. 无圈图的生成树是指顶点与无圈图相同、边集是无圈图的边集子集, 且含边数最少的连通子图. 图2中T1是完全图K8的生成树, 它包含K8中的所有9个顶点, 边集是完全图K8边集的子集, 且包含了最小数目的边数.
|
图 1 Harary图
|

|
图 2 完全图K8和它的生成树T1 |
由构造的Harary图
步骤1. 画出边(1, v+1)和(1, m-v+1), v=1, 2, …,
步骤2. 令
步骤3. 令q=p+1, 重复步骤2画出边(m−q+1, m−q−j+1), (m−q−j+1, m−q−2j+1), …, 当存在从顶点m−p+1到顶点1的路径时停止, 否则转至步骤1.
图3为基于
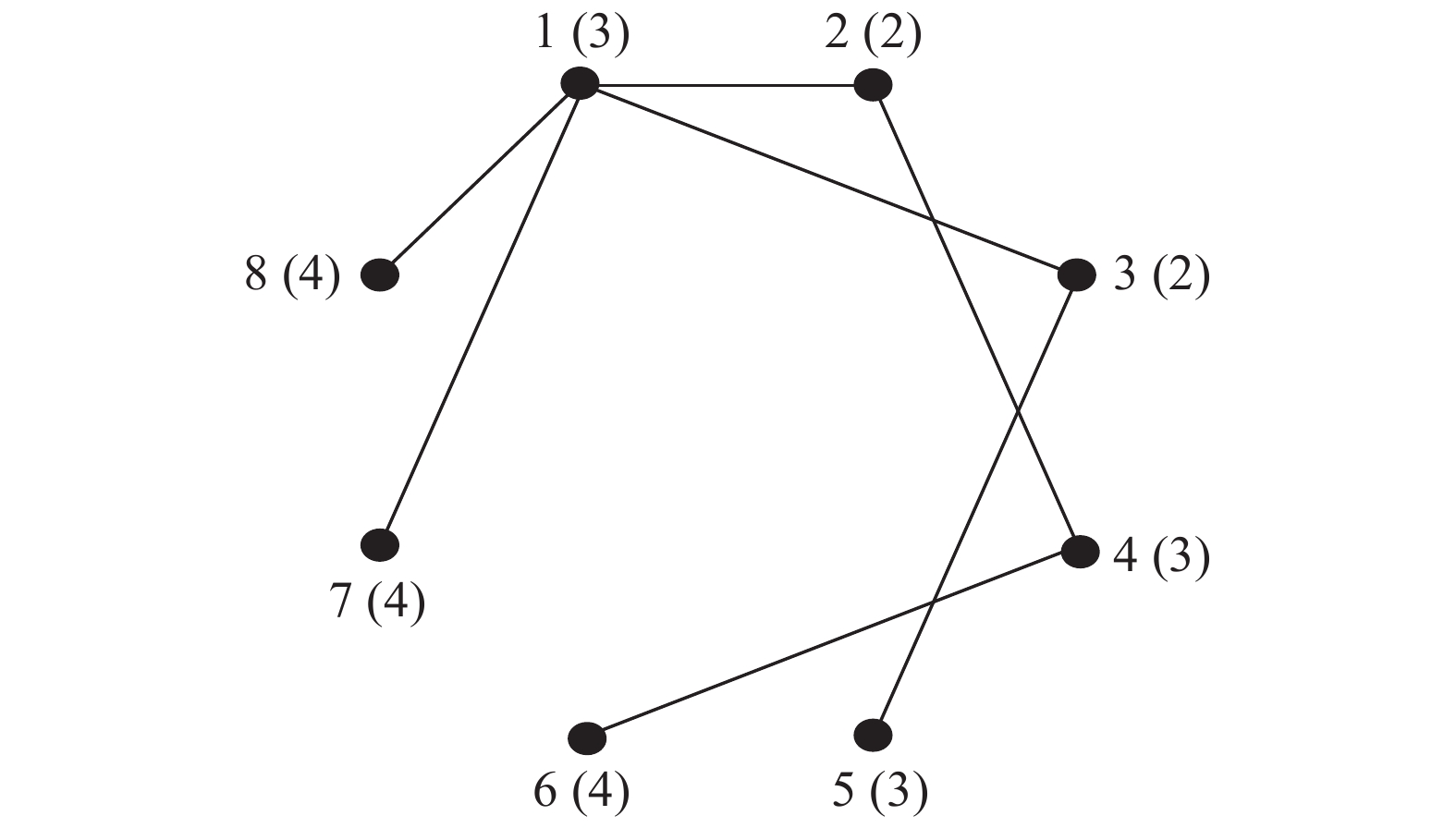
对于连通图G的一个顶点v, v的离心率定义为v到G中除v外所有顶点的距离的最大值. 例如图4中顶点1的离心率值为3, 由于距离顶点1最长的顶点是顶点6, 而从顶点1到顶点6的路径中共经过3个顶点, 即距离为3, 故顶点1的离心率, 其它顶点同理.G的半径定义为G中所有顶点离心率的最小值, 直径则定义为G的最大离心率, 分别记为rad(G)和diam(

|
图 3 基于
|
|
图 4 离心率参考图 |
2 基于Harary图生成树的部分重复码构造 2.1 构造方法
基于Harary图生成树与离心率, 给出重复度为
算法1. 基于Harary图生成树的部分重复码构造
1) 给定一个Harary图的设计参数k和m, 其中k为每个节点所连接的节点个数, 即节点的度, m为顶点个数, m>0.本文暂且只考虑k为偶数的情况.
2) 根据给出的设计参数k和m构造Harary图.
3) 选定Harary图上任一顶点作为顶点1, 并从顶点1开始给Harary图的顶点顺时针编号, 每个顶点存储与其编号相同的数据块.
4) 由构造的Harary图以顶点1为起始顶点构造生成树.
5) 对得到的生成树的顶点按离心率分组, 将第一个生成树G的顶点按离心率分为
6) 按照所需构造部分重复码的重复度
7)由生成树顶点按离心率的分组得到关联矩阵
| $\scriptstyle \scriptstyle{m_{s,t}} = \scriptstyle\left\{ {\begin{array}{*{20}{l}} \scriptstyle{1,}&\scriptstyle{{\text{若}}{v_t}{\text{与}}{e_s}{\text{相关联}}}\\ \scriptstyle{0,}&\scriptstyle{\text{其它情况}} \end{array}} \right. $ |
再将生成树的关联矩阵等价为FR码的关联矩阵, 关联矩阵的行向量对应FR码的存储节点, 列向量对应FR码的编码块.行向量的重表示表示节点存储容量
综上, 重复度为
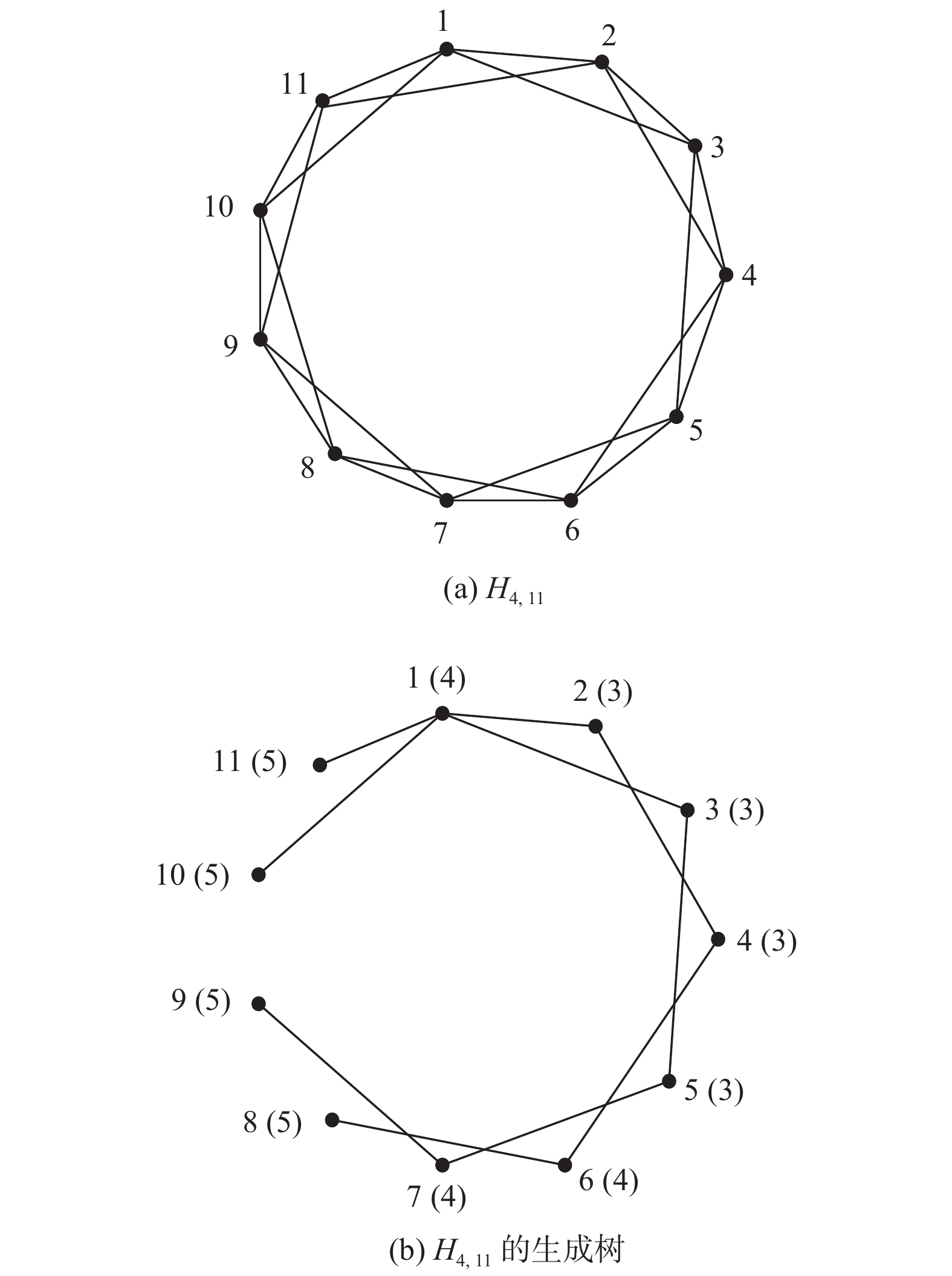
具体地, 我们以构造
|
图 5 |
将图5(b)中给出的生成树的顶点按离心率分组, 相同离心率顶点对应的数据块写入同一分组. 为满足重复度
| ${{M}} = {\kern 1pt} \left[ {{\rm{ }}\begin{array}{*{20}{c}} 0&1&1&1&1&0&0&0&0&0&0 \\ 1&0&0&0&0&1&1&0&0&0&0 \\ 0&0&0&0&0&0&0&1&1&1&1 \\ 0&0&0&1&1&1&1&0&0&0&0 \\ 0&0&1&0&0&0&0&1&1&0&0 \\ 1&1&0&0&0&0&0&0&0&1&1 \\ 0&0&0&0&0&1&1&1&1&0&0 \\ 0&0&0&0&1&0&0&0&0&1&1 \\ 1&1&1&1&0&0&0&0&0&0&0 \end{array}} \right]$ |
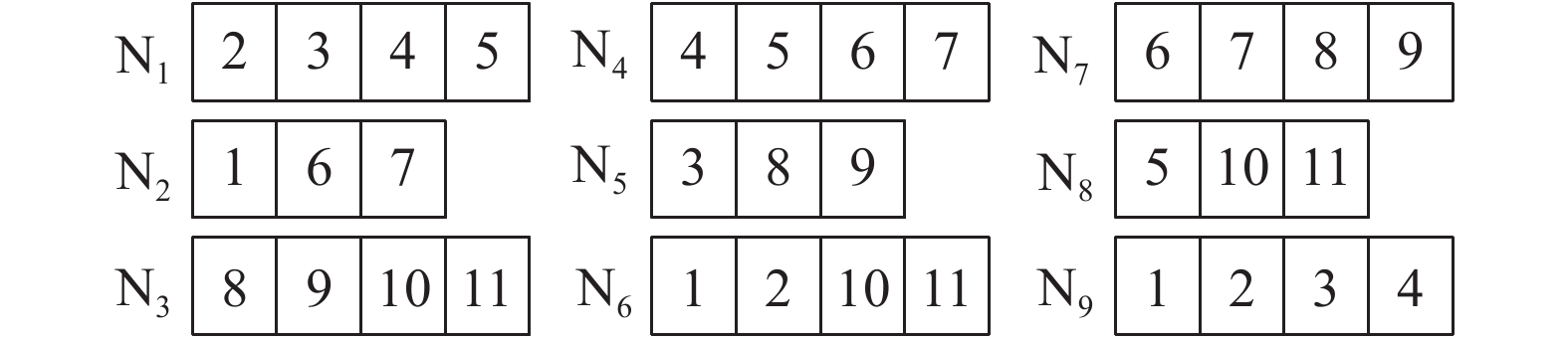
根据关联矩阵M, 构造重复度
|
图 6 FR码 |
2.2 故障节点修复
本论文构造的任意FRSH码都包含
(1) 当单个节点失效时, 新生节点从存活平行类中下载失效节点对应数据块, 即可完成修复. 如节点N1故障时, 损坏的数据块2、3、4、5可从剩余两个平行类N4、N5、N6或N7、N8、N9中下载. 这里选择连接存活节点N4、N9并分别下载4、5、2、3, 即可修复故障节点N1.
(2) 当多个节点同时出现故障, 由于仍至少存在一个平行类包含全部数据块, 而本方法构造的FR码的任一平行类中包含的节点个数等于离心率分组数n, 故至多连接n个节点即可完成修复. 具体地, 当多个故障节点所包含的数据块个数
(3) 当多个节点同时出现故障, 且多个故障节点所包含的数据块个数
综上, 对于重复度为
基于Harary图生成树构造的FR码的性能分析主要集中在修复局部性、修复带宽开销和运算复杂度这几方面, 并将其与传统的RS码和简单再生码(Simple Regenerating Codes, SRC)进行性能比较. 表1给出了SRC、RS码与FRSH码在一般情况下的的节点存储开销、修复带宽开销以及修复局部性的计算公式, 之后我们会在给定具体文件大小和编码数据等条件下用柱状图的形式把上文构造的
| 表 1 几种编码方案的性能分析 |
3.1 修复局部性
修复局部性是衡量构造出的部分重复码性能的重要指标之一, 其定义为节点故障修复过程中连接的存活节点数目, 即磁盘I/O开销. 此处为方便比较, 我们假设原文件大小M=1000 Mb, 存储节点数则为
当单节点出现故障时, SRC在修复失效节点时需要连接2f个节点, 这里取
在两节点故障的情况下, SRC与(11, 8)RS码都需要连接
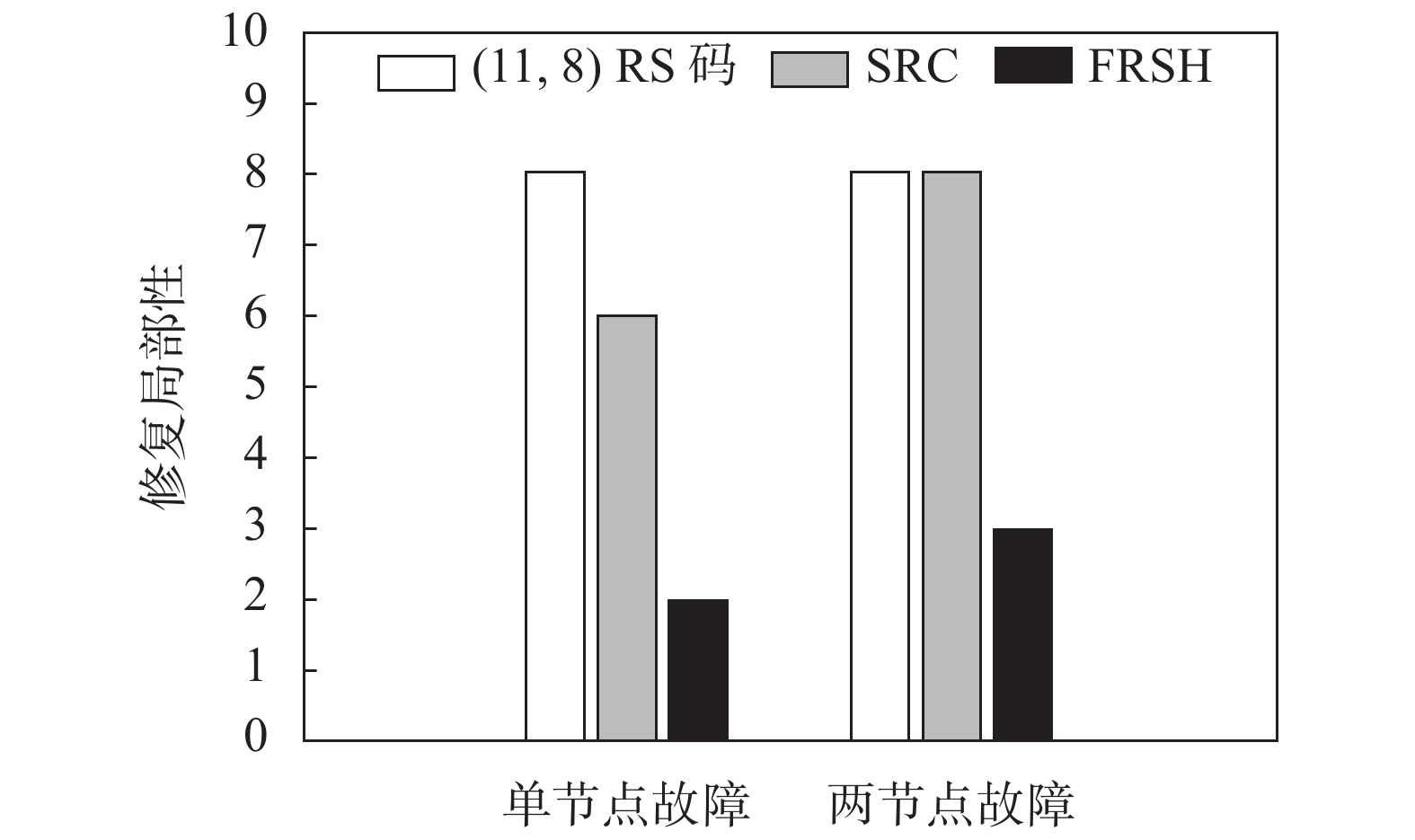
|
图 7 修复局部性 |
另与基于图因子构造的部分重复码相比, 在单节点故障时两种部分重复码都需要连接两个节点进行修复; 在两节点故障时, 基于图因子的部分重复码需要连接4个节点进行修复, 而FRSH码至多需连接3个节点进行修复, 可见在两节点故障时FRSH码具有显著优势.
3.2 修复带宽开销在单节点故障的情况下, SRC需下载
当两节点同时故障时, RS码与SRC的带宽开销均为M. FRSH码的带宽开销为
假设原文件大小为M=1000 Mb, 存储节点数

|
图 8 修复带宽开销对比 |
3.3 构造算法运算复杂度
除去修复局部性与修复带宽开销这两种直观性能, 构造算法复杂度体现了算法在执行时的难易程度, 是衡量一个算法好坏的重要指标. 所谓运算复杂度, 即将算法写成程序在实际的计算机系统中运行时涉及的计算量. 本文构造的FRSH码构造时不需要任何计算量, 只需调节Harary图与其生成树的参数即可. 相较于可达到同等性能的FRC, 减少了大量的运算时间.
将基于Harary图生成树的FRSH与运用图因子分解构造的FRC[17]在构造算法运算复杂度进行对比分析, 在文献[17]中, 构造算法时运用到了加法,乘法运算和基于一次方程上的运算共3种运算方式, 相较于本文仅需调整Harary图参数, 可知本文的构造算法运算复杂度更优.
4 结论与展望针对部分重复码的有效修复问题, 本文基于Harary图生成树构造出了一种新型的部分重复码. 这种FRSH码在构造方面的优势在于参数选择范围较广且运算复杂度极低. 在性能方面, 实验结果表明, 相较于现有的RS码和SRC, FRSH码在修复带宽开销、修复局部性等方面得到了更低的开销, 且改善了修复效率, 并将故障节点的修复时间缩短; 又与可达到类似性能的图因子分解的部分重复码在运算复杂度方面进行比较, 得出本文的构造算法运算复杂度更优.
| [1] |
Shafer J, Rixner S, Cox AL. The hadoop distributed filesystem: Balancing portability and performance. 2010 IEEE International Symposium on Performance Analysis of Systems & Software (ISPASS). White Plains, NY, USA. 2010. 122–133.
|
| [2] |
Liu Y, Vlassov V. Replication in distributed storage systems: State of the art, possible directions, and open issues. 2013 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery. Beijing, China. 2013. 225–232.
|
| [3] |
Silberstein M, Ganesh L, Wang Y, et al. Lazy means smart: Reducing repair bandwidth costs in erasure-coded distributed storage. Proceedings of International Conference on Systems and Storage. New York City, NY, USA. 2014. 1–7.
|
| [4] |
Papailiopoulos DS, Dimakis AG, Cadambe VR. Repair optimal erasure codes through hadamard designs. IEEE Transactions on Information Theory, 2013, 59(5): 3021-3037. DOI:10.1109/TIT.2013.2241819 |
| [5] |
Dimakas AG, Godfrey PB, Wainwright MJ, et al. Network coding for distributed storage systems. 26th IEEE International Conference on Computer Communications (INFOCOM 2007). Spain. 2007. 2000–2008.
|
| [6] |
Rawat AS, Silberstein N, Koyluoglu OO, et al. Optimal locally repairable codes with local minimum storage regeneration via rank-metric codes. 2013 Information Theory and Applications Workshop (ITA). San Diego, CA, USA. 2013. 1–8.
|
| [7] |
El Rouayheb S, Ramchandran K. Fractional repetition codes for repair in distributed storage systems. 2010 48th Annual Allerton Conference on Communication, Control, and Computing (Allerton). Allerton, IL, USA. 2010. 1510–1517.
|
| [8] |
Rai BK, Dhoorjati V, Saini L, et al. On adaptive distributed storage systems. 2015 IEEE International Symposium on Information Theory (ISIT). Hong Kong, China. 2015. 1482–1486.
|
| [9] |
Wang J, Wang TT, Liu XY, et al. Locally repairable codes based on fractional repetition codes in distributed storage systems. 14th International Conference on Wireless Communications, Networking and Mobile Computing. Lancaster, UK. 2018. 578–587.
|
| [10] |
Olmez O, Ramamoorthy A. Repairable replication-based storage systems using resolvable designs. 2012 50th Annual Allerton Conference on Communication, Control, and Computing (Allerton). Monticello, IL, USA. 2012. 1174–1181.
|
| [11] |
Olmez O, Ramamoorthy A. Constructions of fractional repetition codes from combinatorial designs. 2013 Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA. 2013. 647–651.
|
| [12] |
Zhu B, Li H, Hou HX, et al. Replication-based distributed storage systems with variable repetition degrees. 2014 Twentieth National Conference on Communications (NCC). Kanpur, India. 2014. 1–5.
|
| [13] |
Silberstein N, Etzion T. Optimal fractional repetition codes based on graphs and designs. IEEE Transactions on Information Theory, 2015, 61(8): 4164-4180. DOI:10.1109/TIT.2015.2442231 |
| [14] |
Aydinian H, Boche H. Fractional repetition codes based on partially ordered sets. 2017 IEEE Information Theory Workshop (ITW). Kaohsiung, China. 2017. 51–55.
|
| [15] |
Papailiopoulos DS, Luo JQ, Dimakis AG, et al. Simple regenerating codes: Network coding for cloud storage. 2012 Proceedings IEEE INFOCOM. Orlando, FL, USA. 2012. 2801–2805.
|
| [16] |
Kashyap N, Mukherjee M, Sankarasubramaniam Y. On the secret key capacity of the Harary graph PIN model. 2013 National Conference on Communications (NCC). New Delhi, India. 2013. 1–5.
|
| [17] |
余春雷, 王静, 王秘, 等. 图因子分解的部分重复码构造. 中国科技论文, 2019, 14(11): 1260-1264. |
 2021, Vol. 30
2021, Vol. 30


