目前, 随着工业化进程的加快、技术的发展、人民生活水平的提高、人口的快速增长等因素, 能源消耗特别是石油和煤炭的消耗量不断增加, 同时, 石油和煤炭燃料排放出大量的温室气体, 这将加速全球气候变化, 例如全球变暖, 海平面上升和各种次生灾害频繁发生^[1]. 因此, 天然气作为一种相对清洁的能源, 已经引起了各国政府的重视, 并成为世界各国政府主要需求能源之一. 另一方面, 天然气需求量的模糊性增加了能源分配的复杂性, 并且天然气供应不足会给经济和社会带来危害. 此外, 在天然气购买方面, 天然气购买合同属于严格的收付合同类型, 这意味着当人们违反合同规定时, 存在更大的赔偿风险^[2]. 在上述情况下, 合理预测天然气负荷对解决这些问题具有重要意义.

在天然气负荷预测领域, 已经有许多不同的方法用于预测天然气负荷. Soldo^[3]和Tamba^[4]对相关工作进行了详细总结, 并根据预测范围、模型类型、地理区域和其他条件进行了排序总结. 天然气负荷预测的模型研究主要包含3类: (1) 基于统计方法的模型: 线性回归方法^[5]、自回归综合移动平均(ARIMA)^[2]、带外生变量的函数自回归模型(FARX)^[6]、二次多元自适应回归样条(CMARS)^[7]; (2) 基本机器学习方法: 极限学习机^[8]、支持向量回归^[9]、BP神经网络^[10]; (3) 深度学习方法: 深度受限Boltzmann机器(DRBM)^[11].

上述一系列适合短期燃气负荷预测的模型是从线性模型到包含机器学习和深度学习的非线性模型这个方向发展的. 后者在过去几十年中得到了广泛的应用, 因为它们能够完美的泛化输入/输出的关系. Jolanta Szoplik^[12]提出了用多层感知器(MLP)来预测燃气. 它是以日历和天气因素作为输入变量来预测波兰城市的燃气负荷. 最后用得到的最优结构MLP对燃气消耗量进行预测, 结果显示预测准确率优于普通线性模型. 自人工神经网络在能源负荷预测建模中的成功应用以来, 许多研究者探索了深度学习在燃气负荷领域的应用. 最近的研究主要集中在循环神经网络(RNN)和长短期记忆(LSTM)网络上. Wei等^[13]建立了一个具有不同预处理方法的LSTM模型, 对我国不同地区的天然气日负荷进行了预测. Hribar等^[14]用GRU方法对单个居民家庭短期负荷数据进行了建模. 上述两个模型的预测准确率相比于普通神经网络更好.

此外, 还有大量的混合预测方法来建模燃气数据, 并通过与单一模型方法相比获得高精度的预测结果, 实际证明了其有效性^[15]. 特别是基于集群智能算法和单模型的组合方法, 在解决复杂非线性预测控制问题上表现出了较好的可靠性^[16]. Karadede等^[17]利用一种特殊的实值遗传算法BGA (Breeder Genetic Algorithm)优化NGD-NLR回归方程的系数, 然后采用模拟退火算法对前面整个系统进行优化. Wei等^[18]提出了一种新的遗传算法, 即生命遗传算法(LGA), 用于短期负荷预测中支持向量回归(SVR)参数的优化, 在LGA得到SVR的最佳参数之后, 将其应用于我国燃气负荷预测. 余等^[19]还提出了一种基于混沌遗传算法优化小波神经网络的组合模型, 其中混沌遗传算法优化了小波神经网络的参数. 其结果比传统的神经网络模型具有更强的鲁棒性和更好的性能. 因此我们可以初步推断, 混合预测技术, 特别是集群智能算法的集成是燃气负荷预测领域的一个潜在的研究方向.

另外, 还有一部分涉及到其他领域的残差修正方法, 这意味着在预测研究中有两个阶段, 分别有一个主模型和一个次模型^[20]. 具体地说, 先用主模型预测初步值, 然后用主模型生成的残差序列作为输入因子, 用次模型即残差修正模型预测残差值. 最后, 混合模型的预测值是由残差值增强的修正值. 其中, 还有一部分研究在第二阶段增加了分解过程. 它们使用不同的分解方法来分解残差序列, 如带自适应噪声的集成经验模式分解(ICEEMDAN)^[21]、经验模式分解(EMD)^[22]、经验小波变换(EWT)^[23]. Niu等^[24]建立了基于BP神经网络和灰色马尔可夫模型的混合负荷预测模型. 其中采用灰色算法对残差修正马尔可夫模型进行了优化. 结果表明, 残差修正法可以大大提高能量场的预测精度. Wang等^[25]提出了残差修正模型, 以提高季节ARIMA预测电力需求的精度. 残差修正模型由粒子群优化(PSO) Fourier方法和季节ARIMA模型组成, 与其它残差修正模型和单一季节ARIMA模型相比, 具有更好的效果. 通过以上残差修正模型在其他领域的成功应用, 我们可以得出一个共同点: 这些残差校正模型的主模型或次模型都是普通模型, 并通过单一的优化算法加以优化, 只有残差序列作为输入因子. 与上述残差修正模型相比, 本文提出了一种新的残差修正混合模型LSTM-BPNN并应用燃气负荷预测领域, 并通过FCGA和Adam两种优化算法对残差修正模型进行了优化. 另外, 引入了两个新的残差因子作为BPNN神经网络的输入变量. 实验结果显示本模型有着更好预测结果.

1 LSTM-BPNN残差修正模型

LSTM-BPNN残差校正模型是一种基于残差分析的混合模型. 首先研究了残差分析在燃气负荷预测领域的可行性. 假设时间步t处的实际和预测天然气负荷分别为 ${G}_{\rm {act}}\left(t\right)$ 和 ${G}_{\rm {pre}}\left(t\right)$ . 实际残差 ${R}_{\rm {act}}\left(t\right)$ 可以表示为正或负:

$ {R_{\rm {act}}}(t) = {G_{\rm {act}}}(t) - {G_{\rm {pre}}}(t) $

(1)

显然, 如果实际残差 ${R_{\rm {act}}}(t)$ 已知, 则t时的最终预测结果 ${G}_{\rm {act}}\left(t\right)$ 可以写成:

$ {G_{\rm {act}}}(t) = {G_{\rm {pre}}}(t) + {R_{\rm {act}}}(t) $

(2)

${R_{\rm {act}}}(t)$ 可以写成:

$ {R_{\rm {act}}}(t) = f({x_1},{x_2},\cdots) $

(3)

其中, x₁, x₂是残差的影响因子. 我们不能预先知道真实残差值 ${R}_{\rm {act}}\left(t\right)$ , 也不能通过式(3)得到真实残值 ${R}_{\rm {act}}\left(t\right)$ , 但是我们可以使用实际残值的近似值, 预测残值 ${R}_{\rm {pre}}\left(t\right)$ . ${R}_{\rm {act}}\left(t\right)$ 可以写成:

$ {R_{\rm {act}}}(t) \approx {R_{\rm {pre}}}(t) = f({x_1},{x_2},\cdots) $

(4)

因此式(2)可以重写为:

$ {G_{\rm {act}}}(t) = {G_{\rm {pre}}}(t) + {R_{\rm {pre}}}(t) $

(5)

显然, 如果预测的残差 ${R_{\rm {pre}}}(t)$ 是已知的. 只要预测残值更接近实际残值, 整个残差预测模型的精度就会更高.

本文中的LSTM-BPNN残差修正模型有主模型和次模型组成. LSTM-BPNN的主模型是长短期记忆网络(LSTM), 它属于一组强大的连接主义模型, 是前馈神经网络的超集^[26]. LSTM的主要特点是记忆上一个时间步长的处理状态, 并利用该状态影响下一个时间步长的输出, 使LSTM能够学习天然气负荷序列中的长期时间步内容.

LSTM-BPNN的次模型是BP神经网络. 结构合理的BP神经网络在理论上可以逼近任何非线性连续函数. BPNN的这一特性非常适合于复杂残差序列的预测.

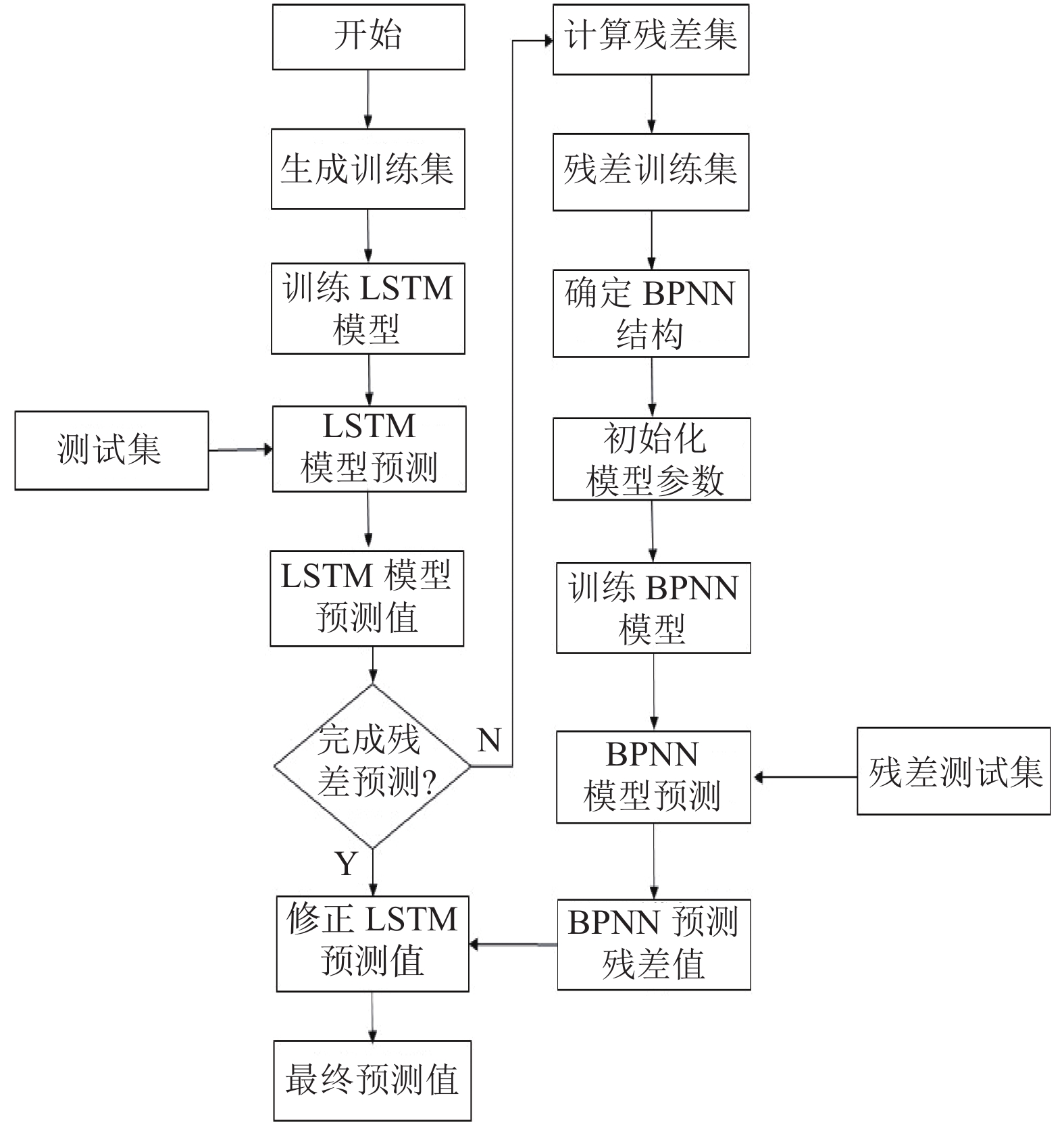
图1中LSTM-BPNN残差修正模型的处理流程如下:

(1) 利用6个输入因子建立了LSTM预测模型. 将经过良好训练的LSTM预测模型应用于实际的燃气负荷预测 ${G}_{\rm {pre}}\left(t\right)$ 中, 同时利用(1)得到不同时刻的LSTM预测残差值, 形成历史残差称为残差数据集.

(2) 利用历史残差和其他两个输入变量建立了BPNN残差预测模型. 将经过良好训练的BPNN残差预测模型应用到预测 ${R}_{\rm {pre}}\left(t\right)$ .

(3) 最后通过BPNN残差模型的 ${R}_{\rm {pre}}\left(t\right)$ 和LSTM模型的 ${G}_{\rm {pre}}\left(t\right)$ 得到 ${G}_{\rm {act}}\left(t\right)$ .

2 基于模糊编码遗传算法和Adam算法的LSTM-BPNN残差修正模型

为了提高LSTM-BPNN残差修正模型的预测精度, 进一步采用了两种优化算法, 即模糊编码遗传算法(FCGA)和Adam算法, 形成LSTM-FCGA-BPNN (Adam)混合预测模型.

2.1 LSTM-FCGA-BPNN (Adam)模型中的Adam算法

Adam算法在本模型中主要是替换掉传统的梯度下降方法来当做模型的学习算法. Adam算法是一种自适应学习速率算法. 它易于实现, 计算效率高, 适用于不稳定序列. 采用Adam算法自动调整LSTM-BPNN残差修正方法的学习速率. 该算法的主要更新公式^[27]如下:

$ {g_t} = {\nabla _\theta }{f_t}({\theta _{t - 1}}) $

(6)

其中, t为时间步, $f(\theta )$ 为参数为 $\theta $ 的随机目标函数. ${g_t}$ 是随机目标函数在时间步t上的梯度.

$ {m_t} = {\beta _1}*{m_{t - 1}} + (1 - {\beta _1})*{g_t} $

(7)

其中, $ {\;\beta }_{1} $ 是矩估计的指数衰减率. $ {m}_{t} $ 是有偏的一阶矩估计.

$ {v_t} = {\beta _2}*{v_{t - 1}} + (1 - {\beta _2})*g_t^2 $

(8)

其中, ${\;\beta _2}$ 是矩估计的指数衰减率. ${v_t}$ 是有偏的第二原始矩估计.

$ {M_t} = {m_t}/\left( {1 - \beta _1^t} \right) $

(9)

其中, $ {M}_{t} $ 是经偏差校正的第一矩估计值.

$ {V_t} = {v_t}/\left( {1 - \beta _2^t} \right) $

(10)

其中, $ {V}_{t} $ 偏差修正了第二原始矩估计.

以上公式是Adam算法的主要组成部分. 详见文献[27].

2.2 LSTM-FCGA-BPNN (Adam)模型中的模糊编码遗传算法

模糊逻辑和进化算法的集成方法有很多种. 模糊编码遗传算法(FCGA)属于一种使用模糊工具和基于模糊逻辑的技术来建模不同进化算法组件的方法^[28]. Voigt^[29]提出模糊编码遗传算法与遗传算法(GA)相似, 只是FCGA考虑了个体从基因型到表现型的个体发展水平. 将个体发展过程建模为模糊决策过程. 每个基因值代表一个决策变量, 其值的范围在0到1之间. 然后, 利用FCGA确定BP神经网络的初始权值和阈值. 该流程由3部分组成:

(1)确定BPNN的结构. 根据短期负荷预测的影响因素、输出参数, 分别确定输入节点数、输出神经元数. 此外, 通过不同的实验确定了隐藏节点的最佳数目.

(2)利用FCGA优化BPNN权值和阈值. 一是随机产生种群. 每个种群的个体代表网络权值和阈值. 其次, 通过适应度函数计算适应度值. 最后, 通过遗传操作获得最好的个体.

(3)采用改进的BP神经网络预测残差值. 首先, 用最好的个体初始化. 优化后的BPNN神经网络可以得到准确的残差预测, 并在燃气负荷预测修正中对LSTM初步值进行修正.

FCGA优化BP神经网络的初始权值和阈值具体实现如下:

(1) 确定编码长度

在模糊遗传算法中, 采用模糊编码对BP神经网络的权值和阈值进行编码. 上述参数的编码长度可由 $S{\rm{ = }}({S_1} + {S_2})*R$ 计算(假设R是权重变量或阈值变量的长度, ${S_1}$ 、 ${S_2}$ 是权重、阈值的个数). 本文用的BP神经网络总共有88个权重和17个阈值, 总计105个变量, 每个变量的编码长度为16位, 例如一个变量的16编码为[0.749080193511837,0.05442683983667307, 0.7238417372546847,0.5273699648234291, 0.43384641666838397,0.5355290304176767, 0.39978529076062863,0.09646569126941518, 0.1134641027244716,0.32005458369217543, 0.5170910797868786,0.05364986305779418, 0.11228946802193374,0.6027138276708447, 0.7133844626952214, 0.5184089125501699] 和原先遗传算法的不同点在于这里的每个值是介于[0, 1]之间的数值, 而不是固定的1或0; 这种模糊值很好表示了复杂的个体发展水平, 同时为寻求解的过程提供了鲁棒性, 因此会导致模糊遗传算法的优化性能更好.

(2) 初始种群与适应度函数

随机产生一个个体 ${X_1} = [{x_{11}},{x_{12}},\cdots]$ , 每个元素的范围是[0, 1]. 在适应度函数方面, 基于神经网络输出节点的误差函数L, 模糊遗传算法的总体目标是求L的最小值, 因此个体适应度函数FT是:

$ FT = \frac{L}{N} $

(11)

其中, N是样本总数.

(3) 选择

选择操作的目的是将根据选择率选择的个体替换为每一代种群中的最佳个体. 首先, 根据选择率的值随机生成替换机会. 当一个个体被选中时, 用最好的个体来代替这个个体. 它模拟了最佳个体生存概率较大的生命活动.

(4) 交叉

交叉运算可以用模糊集的并和交算子来完成. 首先, 在每一代群体中随机选取两个个体进行模糊交叉. 然后从双亲中产生两个基因序列. 一是最大基因序列. 另一个是最小基因序列. 因此, 子基因将使用应用于所有模糊最小和最大序列范围的均匀概率分布随机定义. 孩子出生后, 原来的父母就被替换了. 这一过程产生了后代和其他父母代的混合种群.

(5) 突变

基于以下等式, 突变操作替换个体的基因, 这非常不同于基因的简单0,1逆转^[29].

$ Pmutation({\phi _i}) = Pmutation*\frac{{{2^{n - i}}}}{{{2^{n + 1}} - 1}} $

(12)

其中, $Pmutation$ 是均匀突变概率. n是基因总数, i是单个基因在染色体上的位置.

2.3 LSTM-FCGA-BPNN (Adam)燃气负荷预测模型流程

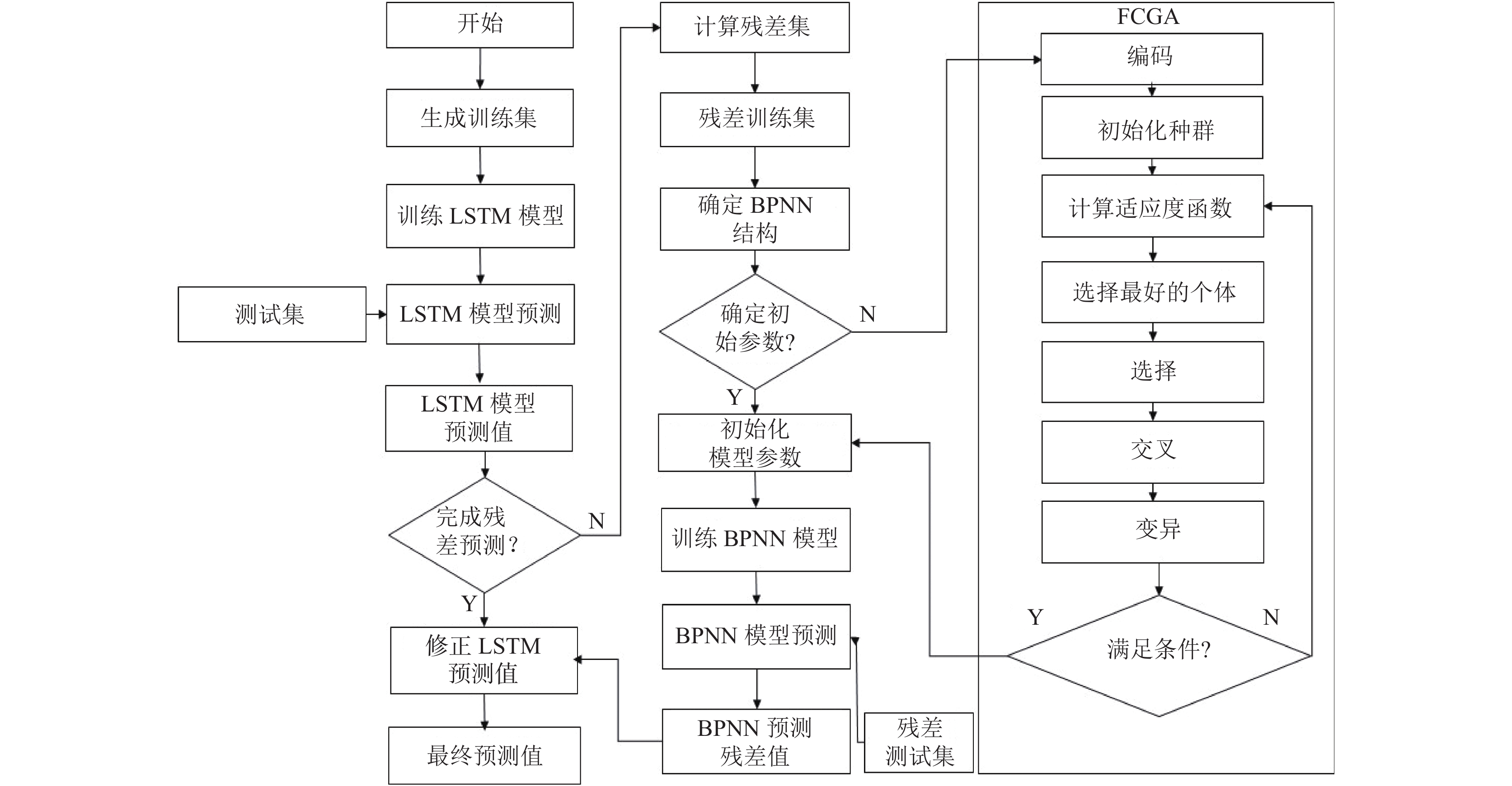
如前所述, LSTM-FCGA-BPNN (Adam)组合模型流程如图2所示.

3 结果和讨论

本节通过历史天然气负荷数据验证了LSTM-FCGA-BPNN(Adam)模型的优越性和稳健性. 也对LSTM-FCGA-BPNN(Adam)模型和其他模型(LSTM、LSTM-BPNN(Adam)、LSTM-GA-BPNN(Adam))进行了性能比较. 所有模型都由Python、TensorFlow和Spyder实现. 模型的主要最佳参数是通过验证集上不断试验和参考相关文献确定的, 如表1所示.

除了表1所示参数外, 还有网络结构参数如LSTM为3层, 每层5个cell, BPNN为2层, 每层8个隐含节点. 这些网络结构参数的选择在考虑模型收敛速度, 在验证集上的拟合效果和参考相关燃气负荷文献确定的. 这些参数的确定保证了网络结构的易用性和鲁棒性. 两个遗传算法的交叉概率和变异概率参数的选择参考了原始文献超参数的设置建议, 以及在验证集上设置的. 交叉概率大一些可以提高种群的多样性, 以及增加在局部解空间的探索强度. 在生物界, 变异概率也是非常稀有的, 因此把变异概率设置的小一些, 防止跳出整个解空间, 利于进入附近的局部解空间.

3.1 数据集和输入变量选择

数据集分为训练集和测试集, 训练集: 2005.11.15~2013.11.15, 共2923个数据集. 测试集: 2013.11.16~2014.5.28, 共194个数据. 其中训练集中选择一部分数据当做验证集来选择超参数. 数据预处理简单地消除了一些异常值. 我们选择以下8个因素作为LSTM-FCGA-BPNN (Adam)的输入, 包括前一天的燃气消耗量、平均温度、周、月、日、预测日的天气条件, 温差(当日气温与前一日气温之差)、预测燃气负荷之差(前一日用气负荷与当日预测用气负荷之差). 模型的输出是预测结果. 其中, 温差和预测燃气负荷差是BPNN模型的输入变量.

3.2 评价指标

为了量化模型的性能, 引入了3个指标: 平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方根误差(RMSE), 这些指标可以定义如下:

$ MAE = \frac{1}{N}\sum\nolimits_{i = 1}^N {|{p_i} - {y_i}|} $

(13)

$ MAPE = \frac{1}{N}\left| {\frac{{{p_i} - {y_i}}}{{{y_i}}}} \right|*100{\text{%}} $

(14)

$ RMSE = \sqrt {\frac{1}{N}\sum\nolimits_{i = 1}^N {{{({p_i} - {y_i})}^2}} } $

(15)

其中, N是时间序列的长度; y是实际数据; p是预测值.

3.3 预测结果讨论

表2显示了各个模型在数据集上的平均预测误差. 每个模型的预测重复50次, 以获得平均预测误差. 所有模型的MAPE都低于10%, 根据Lewis基准^[13], 这是准确的且符合要求的(≥50%). 这一事实表明, 在燃气负荷预测领域, 各种预测模型都是可行的, 上海市的用气趋势与其他地区相比是相对稳定的^[13], 作者认为, 造成这种现象的主要原因是上海市冬季平均气温在1℃左右, 也就是说温差并不大.

对于单一模型, BPNN的MAPE为8.38%, LSTM模型的MAPE为7.16%. 两种模型的MAPE值相差0.012. 这一事实支持LSTM模型在具有相同的输入变量下可以获得相比于普通机器学习的模型(BPNN)好的性能. 在燃气负荷预测中, LSTM方法是一种较好的方法.

与BPNN和LSTM模型相比, LSTM-BPNN和LSTM-BPNN(Adam)的MAPE均保持较低值. 上述两种残差模型的优势百分比至少为1.1%. 这一结果的主要原因是增加了残差分析. 结果表明, 残差分析是一种能显著提高燃气负荷预测精度的方法, 残差具有重要的信息价值, 值得认真研究. 上述两个新变量(温差和预测气差)在残差模型的成功应用也表明, 影响残差序列的不仅仅是前几天的残差序列. 这一结果也证实了残差分析在其他领域的成功应用. LSTM-BPNN(Adam)模型的MAPE略高于LSTM-BPNN模型, 约高0.1%, 说明Adam算法对提高LSTM-BPNN模型的精度起着关键作用. 研究结果还表明, 采用优化算法解决残差模型固有的缺点, 可以进一步提高燃气负荷预测精度, 有利于燃气负荷管理. 因此, 现阶段LSTM-BPNN(Adam)作为天然气日负荷预测的核心模型.

将遗传相似算法与LSTM-BPNN (Adam)相结合是必要的, 因为在大多数情况下, 遗传算法和FCGA都能减小燃气负荷预测模型的预测误差, LSTM-GA-BPNN(Adam)和LSTM-FCGA-BPNN (Adam)的MAPE分别为6.02%、5.91%, 高于前4种模型, 特别是高于前4种模型相同类型的残差模型(LSTM-BPNN, LSTM-BPNN (Adam)), 平均也至少高出0.3%. 这种优势是由于GA-相似算法为LSTM-BPNN (Adam)模型找到了很好的初始解空间. 结果表明, 进一步优化残差模型可以大大提高燃气负荷预测的精度. 这也表明了上述混合模式在剩余分析领域的优越性. 在第3组中, LSTM-FCGA-BPNN (Adam)模型的MAPE比LSTM-GA-BPNN (Adam)模型的MAPE高约1%. LSTM-FCGA-BPNN (Adam)模型之所以稍有优势, 是因为FCGA考虑了个体从基因水平到成熟表型水平的发展. 这一事实证明, FCGA是一种更稳健、更可靠的天然气日负荷预测算法, LSTM-FCGA-BPNN (Adam)模型在这种情况下具有良好的鲁棒性, 可以作为天然气日负荷预测的模型.

在收敛速度方面, 由于FCGA确定BP神经网络的初始权值和阈值, 避免了BP神经网络陷入局部极小值, 采用Adam算法自动调整学习速率, 提高了LSTM-BPNN残差修正模型的性能, 所以在实验组中LSTM-FCGA-BPNN (Adam)模型在解空间寻找最优解时相比于LSTM-GA-BPNN (Adam), LSTM –BPNN, LSTM-BPNN (Adam)收敛更快.

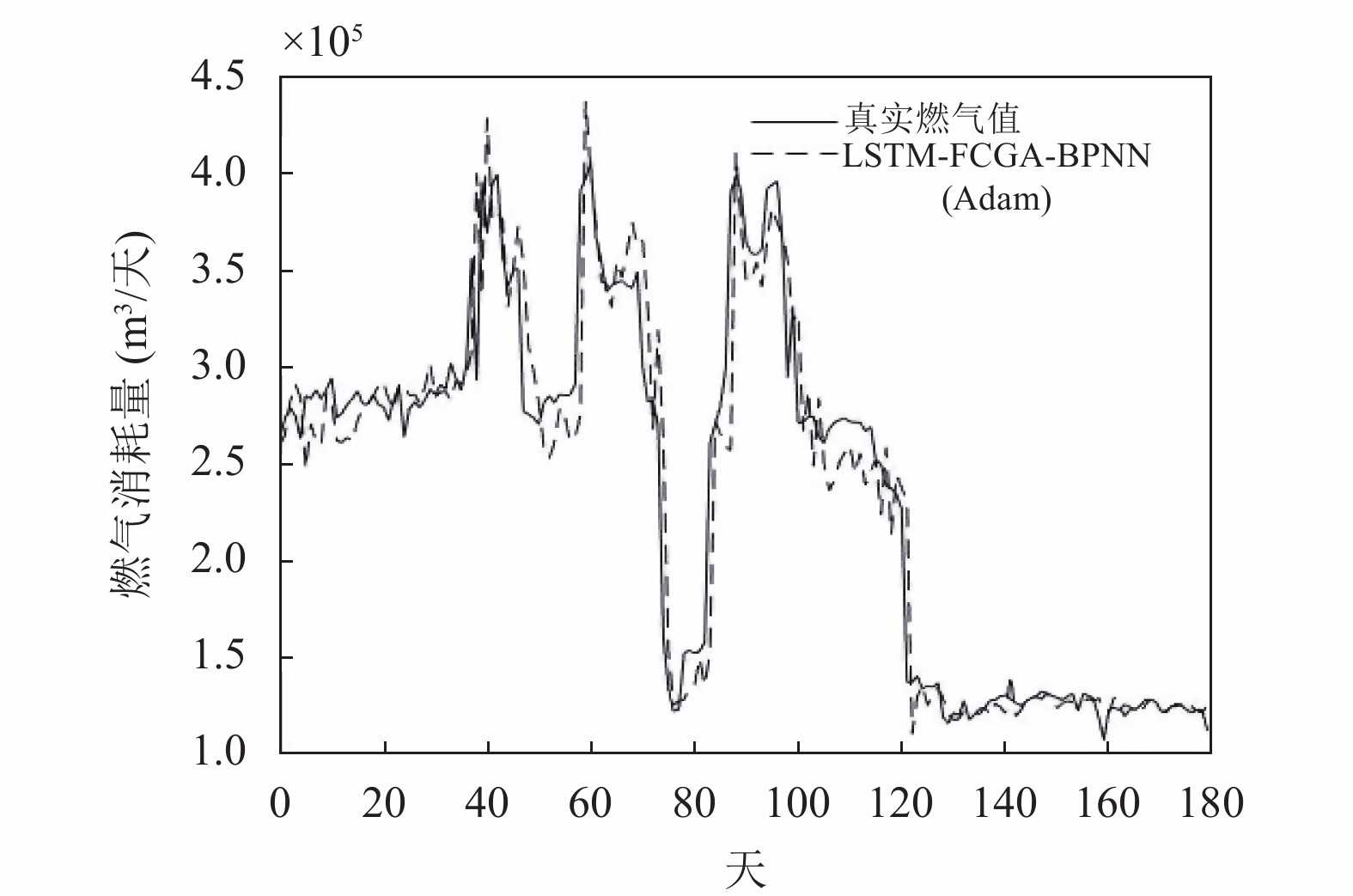
为了更好地观察本模型的性能, 预测结果与实际燃气负荷数据的图形比较如图3所示. 这个图形非常生动地显示了上述结果. 这些数据还表明, LSTM-FCGA-BPNN (Adam)模型能够做出准确的预测, 并具有更强大的获取天然气负荷数据背后特征的能力.

4 结论

本文旨在介绍一种新颖的、预测准确率更高的天然气负荷日预测方法. 该方法是基于LSTM-BPNN残差修正和新输入残差影响因素的混合模型、模糊编码遗传算法(FCGA)和Adam算法. 以LSTM-BPNN残差修正模型为基本模型, 对次日燃气负荷进行预测, 为了提高预测性能, 首先利用Adam算法对LSTM-BPNN残差校正模型的结构进行了优化. 其次利用FCGA对LSTM-BPNN (Adam)模型进行优化. 采用FCGA确定BP神经网络的初始权值和阈值, 避免了BP神经网络陷入局部极小值, 采用Adam算法自动调整学习速率, 提高了LSTM-BPNN残差修正模型的性能

比较了LSTM-FCGA-BPNN (Adam)与LSTM、LSTM-BPNN、LSTM-BPNN (Adam)、LSTM-GA-BPNN (Adam)的预测性能. 根据预测结果, 本文提出的LSTM-FCGA-BPNN (Adam)模型在天然气日负荷预测中具有良好的稳健性, 可以作为一种可靠的预测模型来提供天然气日耗量的准确预测. 此外本文通过日预测的模式预测了194天的时间序列长度, 显示出比较好的结果. 这6个多月的预测长度包含了季节的变更, 非常有利于抓住燃气负荷的主要特征. 本文用的时间长度可以满足上海实际燃气预测范围, 可以让燃气公司提前供气和减少经济损失, 也证明了本文方法应用在较长时间长度也有比较好的效果.

今后, 我们将继续研究残差分析, 继续探索残差中的影响因素, 进一步降低由混合模型引起的计算效率和混合复杂度问题.