计算机网络技术的飞速发展给社会生活和经济发展带来了新机遇, 但网络攻击给网络安全带来了巨大的风险[1, 2]. 分布式拒绝服务攻击(DDoS)在攻击过程使用常见的协议和服务, 准确检测的难度很高. 因此, 对DDoS攻击的高性能检测对维护网络安全具有重要意义[3].
针对DDoS攻击检测问题, 研究人员提出了很多方法[4, 5]. 例如, 文献[6]构建了基于BP神经网络的DDoS攻击检测模型, 采用数据包长度、数据包发送时间等特征检测DDoS攻击, 取得了很好的检测效果. 文献[7]针对软件定义网络攻击, 提出了基于支持向量机和K均值聚类的攻击检测算法, 提高了检测效率. 文献[8]提出了基于组合相关度随机森林的DDoS攻击检测方法, 具有较低的误报率和漏报率. 这些方法均存在特征主观依赖性较强, 检测模型泛化能力差的问题. 文献[9]将深度神经网络应用于DDoS攻击检测, 模型泛化能力较强, 但训练效率较低.
本文首先基于卷积神经网络(CNN)构建了DDoS攻击检测模型, 实现了DDoS攻击的高准确率检测. 然后, 引入粒子群算法(PSO), 对卷积神经网络的卷积核进行优化, 提高模型训练效率, 并与梯度下降方法相结合, 增加模型全局寻优能力.
1 卷积神经网络CNN是一种具有深度结构的前馈神经网络, 广泛应用于计算机视觉及自然语言处理等领域[10]. CNN的主体架构包括卷积层、池化层、全连接层、输入层和输出层, 其中卷积层与池化层是CNN的核心.
1.1 卷积层卷积层输入通常为多维数组, 卷积运算可以看作以卷积核为中心, 不断在输入数据上进行滑动卷积操作的过程, 具体实现过程如下. 首先, 将卷积层中的卷积核与输入数组对应位置的元素进行相乘后计算和值, 然后不断滑动卷积核直到所有输入数据均完成上述操作. 假设CNN的输入数据为二维数组
| ${(x * f)_{ij}} = \sum\limits_{u = 1}^{{n_1}} {\sum\limits_{v = 1}^{{n_2}} {{f_{uv}}{x_{i - u + 1,j - v + 1}}} } $ | (1) |
上述二维数据卷积操作的过程如图1所示.

|
图 1 卷积操作过程 |
传统人工神经网络的输入层、输出层与神经元层之间的连接通常都是由矩阵乘法构建的全连接结构, 结构十分复杂. CNN中, 每个输出并不是与各个输入均连接, 而是只连接部分输入, 有效地减少了网络参数, 降低了网络训练的复杂度. CNN的局部连接使得网络底层只对局部信息进行感知, 在高层将底层信息进行综合, 有效地提高了网络的局部特征提取能力. 并且, CNN的卷积层中, 权值是可以共享的. CNN的局部连接和权值共享使其在训练效率和存储需求上均优于传统神经网络, 具有较低的时间和空间复杂性.
1.2 池化层池化层位于卷积层之后, 通过池化来降低卷积层输出的特征向量, 同时改善训练结果, 避免网络出现过拟合现象. 池化过程是选取某一个位置的总体特征作为该位置的输出, 在保留总体信息的同时, 降低特征参数的维度和网络参数数量. CNN中的常用池化方法有平均池化法和最大池化法, 平均池化是指提取相邻区域特征值的平均值, 最大池化则提取相邻区域内的特征值的最大值, 图2给出了最大池化特征提取过程.

|
图 2 最大池化过程(
|
如果网络输入为
PSO是一种源于鸟群捕食过程的启发式优化算法, 实现疑难问题的优化. PSO结构简单、计算量小、收敛速度快, 且全局寻优能力强, 在函数优化、系统控制等复杂问题优化领域有着十分广泛的应用[11].
卷积核优化是CNN的核心问题, 直接影响了CNN的性能. 考虑到PSO优化算法的优良寻优性能和快速收敛能力, 将其由于优化CNN的卷积核. PSO优化过程可以总结为各个微粒
| ${v_i}(t + 1) = \omega {v_i}(t) + {c_1}{r_1}\left[ {{P_i}(t) - {X_i}(t)} \right] + {c_2}{r_2}\left[ {{P_g}(t) - {X_i}(t)} \right]$ | (2) |
位置更新过程为:
| ${X_i}(t + 1) = {X_i}(t) + {v_i}(t + 1)$ | (3) |
式中,
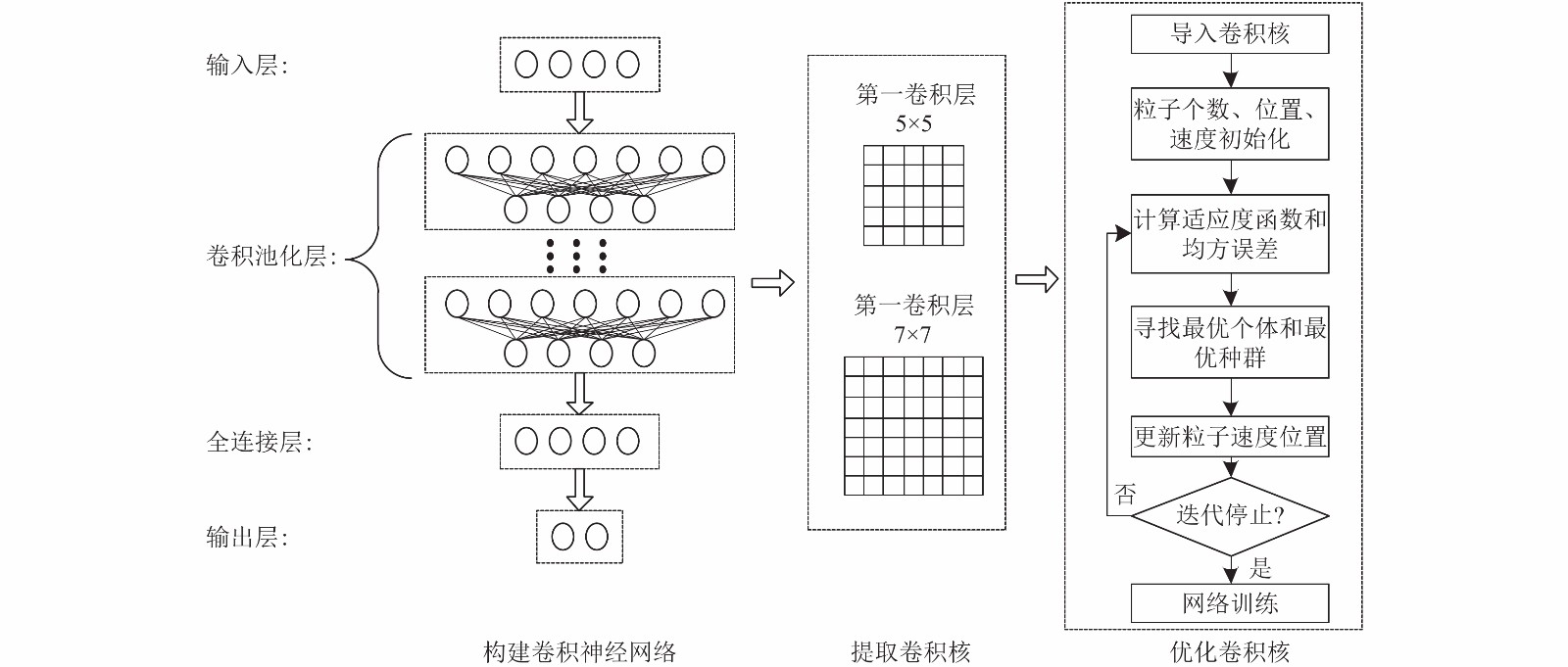
利用CNN实现网络攻击检测具有一定的可行性, 但是存在两个问题, 一是网络容易陷入局部最优值, 二是网络的卷积核难以初始化, 限制了网络性能. 为此, 本文将PSO优化算法引入CNN, 构建了基于优化CNN的攻击检测模型, 模型结构如图3所示, 具体步骤介绍如下.
|
图 3 PSO优化CNN攻击检测模型 |
步骤1. 构建CNN模型. 将DDoS攻击数据输入, 采用随机方式初始化CNN的各层卷积核, 卷积层与池化层交替布置, 池化层特征数量与其前一个卷积层相同, 网络最后为全连接层, 导出一维向量给输出层, 实现网络攻击的检测.
步骤2. PSO优化卷积核. 从CNN的各个卷积层中提取出卷积核作为PSO的初始种群, PSO适应度函数为网络输入与网络输出之间的均方误差. 假设输入输出数据共有n组, 适应度函数可以表示为:
| ${M{SE}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{({T_i} - {P_i})}^2}} $ | (4) |
其中,
步骤3. 梯度下降网络训练. 将步骤2得出的最优卷积核导入到CNN进行训练, 基于梯度下降法实现网络权值寻优, 实现PSO全局最优能力和梯度下降局部最优相结合, 最终实现网络攻击检测.
2.3 关键技术(1) PSO初始化卷积核
从分布式拒绝服务数据训练集中随机选取出部分数据以及对应的分类标签构建测试集合. 根据CNN理论, 网络特征图的数量是由滤波器数量决定的, 而CNN的主要权值就是卷积层中的卷积核, 因此由网络各层的卷积核构建PSO的初始种群. PSO优化的位置信息为整个网络权值空间, 且设置最大粒子速度区间, 位置参数和速度参数上均采用随机初始化方法, PSO种群规模与CNN卷积核个数保持一致.
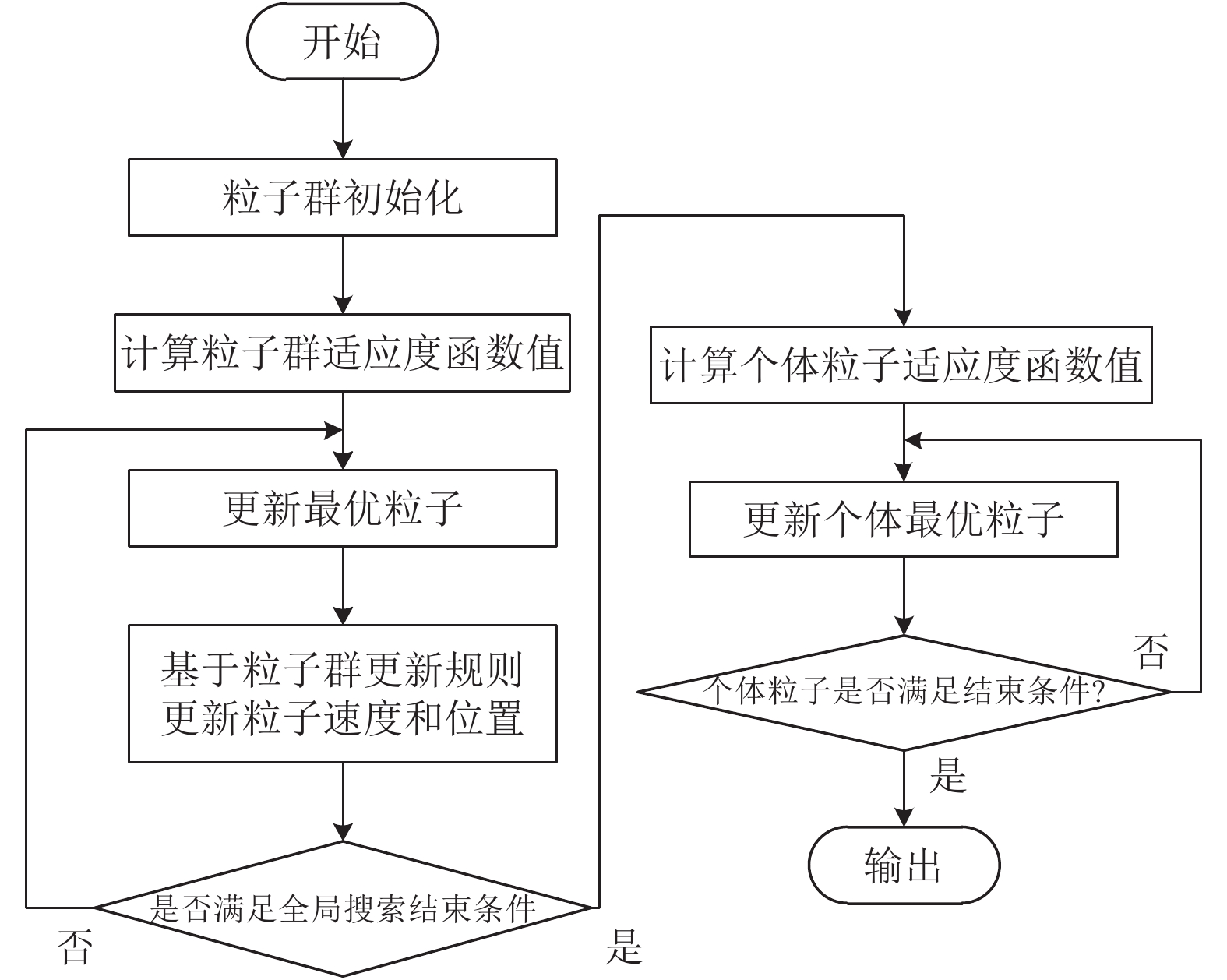
随机选取部分网络攻击数据和对应标签作为CNN的输入, 以网络输出和输入的均方误差作为PSO的适应度函数. 以各个粒子坐标作为粒子位置, 计算个体的适应度函数值, 通过PSO进化不断更新粒子速度和位置, 对比各个粒子的适应度函数值, 当满足迭代终止条件时, PSO寻优结束, 算法具体步骤如图4所示.
|
图 4 PSO优化卷积核流程 |
(2) PSO结合梯度下降
基于PSO的优良全局最优能力, 不断更新迭代粒子位置和速度, 得出一组最优粒子, 用最优粒子初始化CNN卷积核, 对新CNN进行重新训练. 经过卷积和池化后, 特征值输入到全连接层转化为一维特征向量, 最后利用输出层实现网络攻击检测. 输出值与样本标签之间的误差作为反向传播依据, 基于梯度下降法进行网络权值修正. 上述训练过程将PSO全局最优能力与CNN局部搜索能力相结合, 能够有效避免CNN陷入局部最优, 具体流程如图5所示.

|
图 5 PSO结合梯度下降 |
3 实验与分析 3.1 实验条件
实验基于Tensorflow框架构建CNN模型, 采用Python语言实现PSO优化程序, 硬件环境为戴尔T640类型的GPU运算服务器, 软件环境为Windows 10操作系统.
实验数据分为网络正常数据(正常流)和DDoS攻击数据(攻击流), 正常流数据为自动获取, 而攻击流数据为自动获取与人工构建相结合. 数据集总量为10万条, 按照正常流与攻击流比例随机将数据分为训练集和测试集, 其中训练集8万条数据, 测试集2万条数据, 具体如表1所示.
| 表 1 实验数据集(单位: 条) |
3.2 评估指标
利用准确率、召回率、精确率、F1值和混淆矩阵对模型的DDoS攻击检测进行性能评价. 准确率定义为检测模型检测正确的数据数量占总数据量的比例, 计算方法为:
| ${A{CC}} = \frac{{TP + TN}}{{TP + TN + FP + FN}}$ | (5) |
其中, TP表示攻击流样本数据被模型正确检测为攻击流数据的样本数量, TN表示正常流样本数据被模型检测为正常流数据的样本数量, FP表示正常流样本数据被模型检测为攻击流数据的样本数量, FN表示攻击流数据被模型检测为正常流的样本数量.
召回率定义为检测模型判定为攻击流数据占所有攻击流数据的比例, 计算方法为:
| $R = \frac{{TP}}{{TP + FN}}$ | (6) |
精确率定义为检测模型判定为攻击流数据中, 确实为攻击流数据的比例, 计算方法为:
| $P = \frac{{TP}}{{TP + FP}}$ | (7) |
F1值定义为精确率和召回率之间的调和平均值, 能够较好低评估DDoS攻击检测模型的性能, 计算方法为:
| ${F1} = \frac{{2PR}}{{P + R}}$ | (8) |
混淆矩阵是评价检测模型的常用指标, 能够有效描述检测模型检测结果与样本标签之间的匹配程度, 有利于校验模型的检测能力.
3.3 结果分析不同深度CNN的检测能力不同, 目前缺乏设置CNN架构的理论结论. 大量测试结果表明, CNN的架构对于DDoS攻击检测具有较大影响, 实验中选取了4种典型的CNN结构进行对比分析.
考虑到模型训练效率, 采用小批量训练, batch大小设置为50, 共构建了4型CNN, 分别为C3P2F2、C3P3F3、C2P2F2、C2P2F4, 其中C3P3F3表示该CNN有3个卷积层、3个最大池化层和3个全连接层, 其它网络定义相同, 网络激活函数均采用Sigmoid函数. 采用表1中数据集分别对4型CNN进行对比测试, 4型CNN的准确率、召回率、精确率、F1值统计结果如表2所示.
| 表 2 不同类型CNN检测结果(%) |
结果表明, 3层CNN(C3P2F2、C3P3F3)对DDoS网络攻击的检测性能显著优于2层CNN(C2P2F2、C2P2F4). 3层CNN中, C3P2F2的精确度、召回率以及F1值指标性能优于C3P3F3, 但检测准确率不如C3P3F3. 为进一步比较4型CNN对DDoS的检测性能, 图6给出了4型CNN的混淆矩阵.

|
图 6 不同CNN检测混淆矩阵 |
图6表明, 2层CNN对于正常流数据和攻击流数据的判型能力上均弱于3层CNN, 这与表2指标结果保持一致. 对比C3P2F2和C3P3F3混淆矩阵可知, C3P2F2对于攻击流数据的检测能力优于C3P3F3. 在网络运行过程中, 一旦出现DDoS攻击机会对整个计算机网络系统的正常运行带来很大的隐患, 因此网络攻击检测模型必须要对攻击流数据敏感, 因此C3P2F2更适合于符合实际对DDoS攻击进行检测的需求.
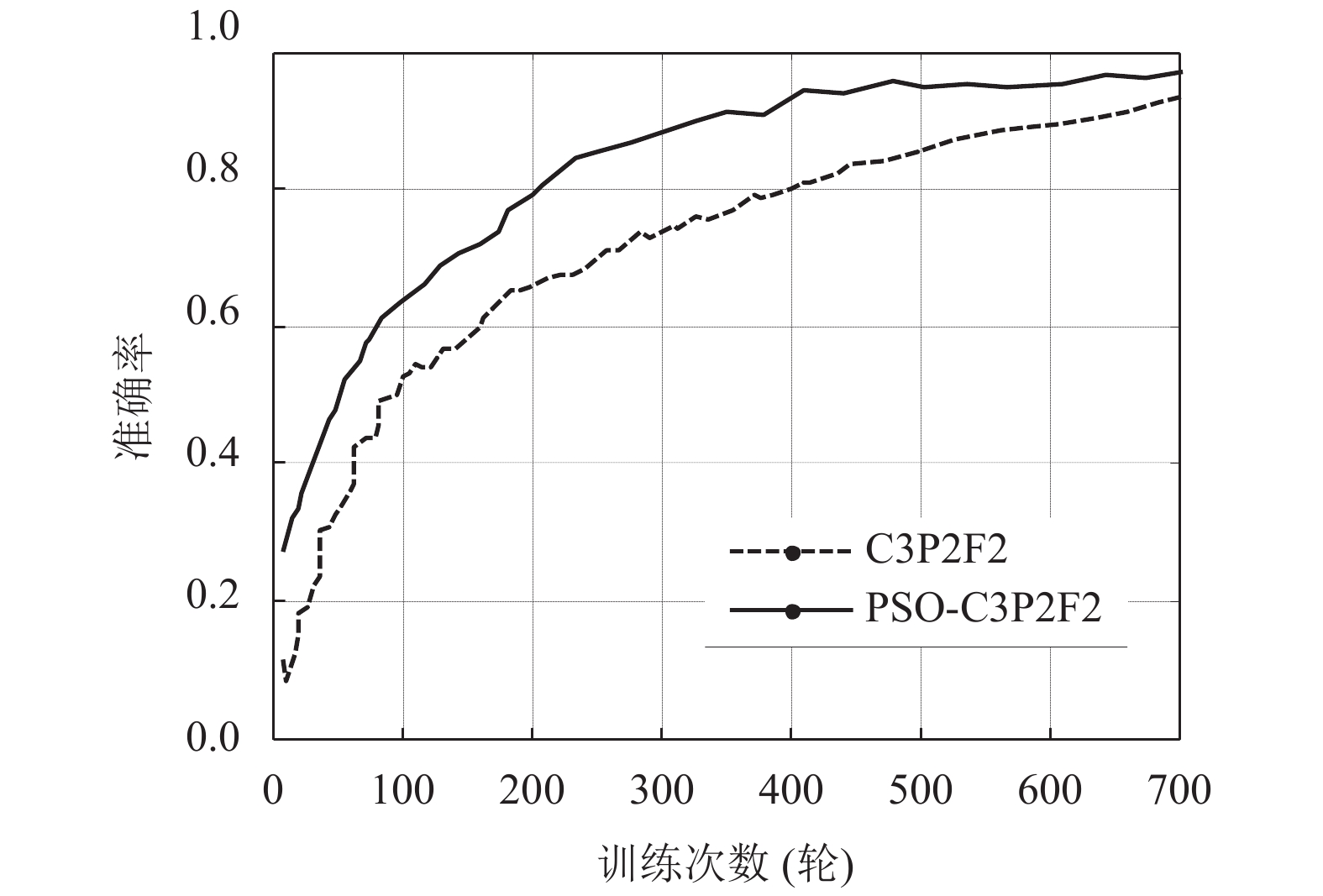
C3P2F2模型检测精度较高, 由于模型层数较深、数据规模大, 因此训练过程中收敛速度慢, 难以满足实际需求, 且易陷入局部最优. 为了提高CNN训练效率以及避免CNN陷入局部最优, 本文构建了基于PSO优化CNN的DDoS攻击检测模型, 下面通过实验测试其性能. 图7给出了原始C3P2F2模型和经过PSO优化后C3P2F2模型检测准确率与训练次数之间的关系.
|
图 7 PSO优化性能测试 |
实验结果表明, 经过PSO优化后, 显著加快了CNN的训练速度. 为了进一步测试本文构建PSO优化CNNDDoS攻击检测模型(PSO-C3P2F2)性能, 将其分别与目前常用DDoS攻击检测模型中的支持向量机模型(SVM)[7]、随机森林(RF)模型[8]进行同等条件下的检测性能对比, 每种模型进行10次试验, 统计指标平均值, 结果如表3所示.
| 表 3 不同模型检测性能对比(%) |
从表3结果可知, C3P2F2模型在各个指标上的性能均优于SVM模型和RF模型, 且PSO-C3P2F2模型相比C3P2F2模型有略微提升. 这是因为, SVM模型和RF模型均需要人为选取特征向量, 不能很好地表征DDoS攻击数据特征, 而C3P2F2模型能够自适应提取隐含在数据中的局部特征, 避免受到主观因素影响, 因此检测性能优于传统机器学习方法. PSO-C3P2F2模型检测性能的提升是由于将PSO的全局寻优能力与CNN局部最优能力相结合, 能够有效避免CNN陷入局部最优.
4 结束语研究了DDoS攻击检测问题, 构建了基于CNN的攻击检测模型, 利用权值共享和最大池化实现了DDoS攻击的高准确率检测. 针对训练效率偏低的问题, 引入PSO对CNN的训练过程进行优化, 提高网络训练效率和全局寻优能力.
| [1] |
于亚芳, 潘耘, 王励成. 命名数据网络中的DoS/DDoS攻击研究综述. 信息技术, 2017(6): 78-82, 87. |
| [2] |
冯晓荣. 基于人工蜂群算法的双门限CRN网络攻击检测算法. 计算机应用与软件, 2019, 36(10): 316-322, 333. DOI:10.3969/j.issn.1000-386x.2019.10.054 |
| [3] |
张龙, 王劲松. SDN中基于信息熵与DNN的DDoS攻击检测模型. 计算机研究与发展, 2019, 56(5): 909-918. DOI:10.7544/issn1000-1239.2019.20190017 |
| [4] |
程杰仁, 罗逸涵, 唐湘滟, 等. 基于LSTM流量预测的DDoS攻击检测方法. 华中科技大学学报(自然科学版), 2019, 47(4): 32-36. |
| [5] |
余学山, 韩德志, 杜振鑫. 基于智能蜂群算法的DDoS攻击检测系统. 计算机科学, 2018, 45(12): 123-129. |
| [6] |
杨可心, 桑永胜. 基于BP神经网络的DDoS攻击检测研究. 四川大学学报(自然科学版), 2017, 54(1): 71-75. |
| [7] |
马乐乐, 束永安. SDN环境下基于机器学习算法的DDoS攻击检测模型. 微电子学与计算机, 2018, 35(5): 15-20. |
| [8] |
李梦洋, 唐湘滟, 程杰仁, 等. 基于组合相关度的随机森林DDoS攻击检测方法. 郑州大学学报(理学版), 2019, 51(2): 23-28, 39. |
| [9] |
Priyadarshini R, Barik RK. A deep learning based intelligent framework to mitigate DDoS attack in fog environment. Journal of King Saud University-Computer and Information Sciences, 2019, 23(3): 55-63. |
| [10] |
罗靖遥, 黄征. 基于CNN分类器和卷积的目标检测. 信息技术, 2017(9): 101-104, 108. |
| [11] |
吴旋, 来兴平, 郭俊兵, 等. 综采面区段煤柱宽度的PSO-SVM预测模型. 西安科技大学学报, 2020, 40(1): 64-70. |
 2021, Vol. 30
2021, Vol. 30


