验证码是一种被广泛应用于互联网安全领域, 可有效防止自动化脚本对服务器进行攻击、区分人类和计算机的图灵测试技术[1]. 较低的分辨率及背景带干扰等特点, 使其对传统的光学字符识别技术(Optical Character Recognition, OCR)具有一定的抵抗能力, 可有效避免金融诈骗、刷单式营销等恶性事件的发生, 因此备受金融证券系统和电商网站的青睐, 被广泛部署于各项服务中, 为建设安全的互联网环境做出了巨大的贡献. 近年来, 计算机视觉技术(Computer Vision, CV)飞速发展, 传统的验证码变得不再安全. 由此引发了验证码生成技术的更新迭代, 出现了带有彩色图形噪声、字符扭曲粘连严重的新型验证码. 对于这种情况, 旋转匹配、支持向量机(Support Vector Machine, SVM)[2,3]等传统算法变得不再适用.
得益于脑科学和神经科学的发展, 有学者提出通过构造人工神经网络(Artificial Neural Network, ANN), 即把众多具有信息处理功能的“神经元”按照一定的方式进行连接, 组成网络反复训练, 来模仿人脑的学习过程, 进而达成“机器以人的方式学习图片特征, 识别验证码”的效果. 1998年, LeCun等人[4]在已有的工作基础上设计了如图1所示的名为LeNet-5的卷积神经网络(Convolutional Neural Network, CNN)并在手写数字的识别任务上取得成功. 这之后, 陆续有研究者设计出更深层的网络. 其中, 文献[5]设计的AlexNet首先将修正线性单元ReLU作为网络各层的激活函数, 大大缩短了模型收敛所需的时间; 文献[6]提出的VGG16和VGG19则在加深网络层数的同时使用小卷积核代替大卷积核, 不仅减少了卷积操作带来的计算量, 还提升了模型提取图像特征的精度; 文献[7]设计的GoogLeNet提出使用多尺度稀疏结构, 保持网络结构稀疏性的同时, 充分利用了密集矩阵的高计算性能. 实验证明, 将它们用于验证码识别都可取得不错的成绩. 卷积神经网络深度的增加带来更强的图像特征表达能力的同时, 优化难、训练成本高等问题也接踵而至, 参数数量的激增, 又令模型变得十分“臃肿”, 限制了其在移动端及工业控制设备等算力弱、存储小的平台上的部署. 如何在减少参数数量的同时获得更强的特征表示能力和更高的识别成功率, 便是一个十分重要的问题.
基于上述分析, 本文设计了一种融合了空洞卷积和多尺度稀疏结构的轻量神经网络用于复杂验证码图像的特征提取和识别, 计算网络输出的Sigmoid交叉熵作为模型损失率, 采用RAdam算法做优化, 其特点及计算过程在第1.3节中介绍.

|
图 1 LeNet-5的结构 |
1 设计方案 1.1 图像预处理模块
对图像进行适当的预处理, 可有效消除图像中无关识别的信息[8], 降低维度, 既增强了特征因素的可检测性, 也有助于神经网络设计的轻量化. 本次实验中对原始样本集的预处理由统一尺寸及灰度转换两部分组成. 其中, 灰度转换将三通道的验证码图像转换为单通道[9], 这使得参与计算的数据量大大减少, 既有利于图像的进一步处理, 也降低了神经网络的负载, 使其变得更轻. 其转换方法可用式(1)表示:
| $ Gray \leftarrow (19\;595R + 38\;469G + 7472B) \gg 16 $ | (1) |
轻量神经网络的设计要遵循几个原则: 尽量完整的网络结构、不宜过多的层数以及尽可能少的内存访问成本(Memory Access Cost, MAC)[10]. 基于此, 本文设计了如图2所示的名为LNet的轻量神经网络, 其参数信息如表1所示. 其中, 卷积操作使用如图3(a)所示的大小为3×3, 扩张率为2的空洞卷积核(atrous convolutions), 相比于如图3(b)所示的传统卷积核, 可在不增加参数的前提下获得更大的感受野(Receptive Field, RF)[11]; 使用1×1卷积核在不损害模型表达能力的前提下大大减少参数量和计算量[12]. 使用Leaky ReLU[13]作为各层的激活函数来缓解梯度消失问题, 不使用修正效果更好的PReLU函数的原因在于PReLU会引入新的超参, 加重模型的训练负担. Leaky ReLU的修正方法可用式(2)表示(a为常数).
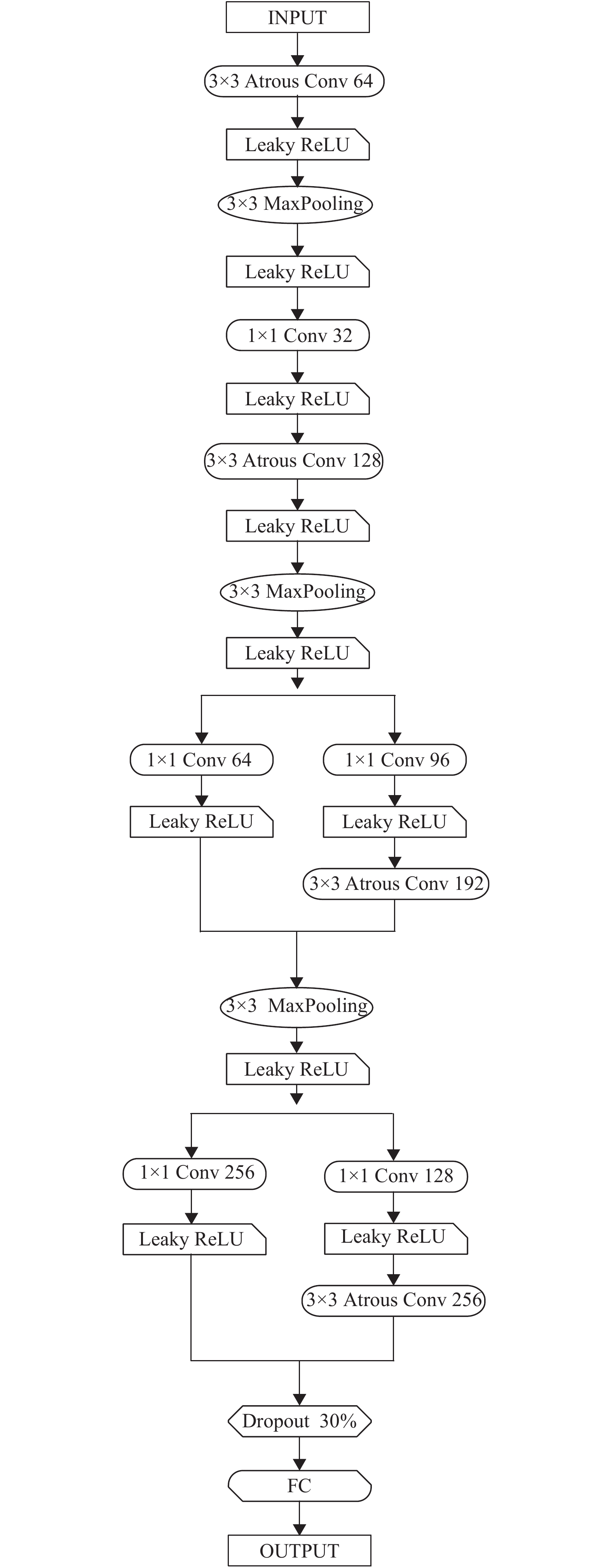
|
图 2 轻量神经网络 |
| $ f(x) \leftarrow \max (ax,x) $ | (2) |
交叉熵在信息论中可用于度量两个概率分布的差异性. 适用于验证码识别任务的Sigmoid交叉熵作为损失函数可用式(3)表示.
| $C \leftarrow {{ - 1/n}}\sum {[y\ln a + (1 - y)\ln (1 - a)]} $ | (3) |
| 表 1 LNet参数信息 |

|
图 3 普通卷积核和空洞卷积核 |
RAdam由Liu等人[14]提出, 兼有Adam优化器[15-17]和随机梯度下降法(Stochastic Gradient Descent, SGD)[18]两者的优点, 可在获得较快收敛速度的同时有效避免掉入局部最优解的陷阱. 根据方差分散度动态地打开或关闭自适应学习率, 在大数据集上表现良好且内存需求不高, 其计算过程可用式(4) ~ 式(12)表示:
| $ {g_t} \leftarrow {\Delta _\theta }{f_t}({\theta _{t - 1}}) $ | (4) |
| $ {m_t} \leftarrow {\beta _1}{m_{t - 1}} + (1 - {\beta _1}){g_t} $ | (5) |
| $ {\nu _t} \leftarrow {\beta _2}{\nu _{t - 1}} + (1 - {\beta _2})g_t^2 $ | (6) |
| $ \mathop {{m_t}}\limits^ \wedge \leftarrow {m_t}/\left( {1 - \beta _1^t} \right) $ | (7) |
| $ {\rho _t} \leftarrow {\rho _\infty } - 2t\beta _2^t/\left( {1 - \beta _2^t} \right) $ | (8) |
| $ {\rm{If}}\;\;({\rho _\infty } > 4):\;\;\;\;\;\;{\mathop \nu \limits^ \wedge}_t \leftarrow \sqrt {{\nu _t}/\left( {1 - \beta _2^t} \right)} $ | (9) |
| $ r \leftarrow \sqrt {\frac{{({\rho _t} - 4)({\rho _t} - 4){\rho _\infty }}}{{({\rho _\infty } - 4)({\rho _\infty } - 2){\rho _t}}}} $ | (10) |
| $ {\theta _t} \leftarrow {\theta _{t - 1}} - {\partial _t}{r_t}\mathop {{m_t}}\limits^ \wedge /\mathop {{\nu _t}}\limits^ \wedge $ | (11) |
| $ {\rm{Else}}:\;\;\;\;\;\;\;{\theta _t} \leftarrow {\theta _{t - 1}} - {\partial _t}\mathop {{m_t}}\limits^ \wedge $ | (12) |
其中, 式(4)计算第i步时的梯度; 式(5)和式(6)分别计算移动量的一阶矩估计和二阶矩估计; 式(7)对一阶矩估计的值做偏差修正; 式(8)计算SMA (Simple Moving Average)的最大长度; 式(9)对二阶矩估计的值做偏差修正; 式(10)获得方差的修正范围.
2 数据集与实验环境本文借助爬虫工具收集了100万张如图4所示的带有彩色图形噪声、字符扭曲粘连的验证码图像建立主数据库IDB1, 其中每张图像的原始大小为180×92; 分别采集来自大连理工大学综合教务系统和微信开发者平台的6万张验证码图像建立数据库IDB2和IDB3, 每张图像的原始大小为168×84. 经预处理后的样本按照98:1:1的比例划分为训练集(train set)、验证集(validation set)和测试集(test set). 其中训练集用于训练模型, 在梯度下降(gradient descent)的过程中确定网络各层的权重和偏置等参数; 验证集用于学习率、深度等超参数(hyperparameter)的优化[19]; 测试集则用于对模型性能的最终评估.

|
图 4 超分辨率重建后的验证码图像示例 |
本文模型构建及算法设计基于开源框架PyTorch实现, 实验中模型训练的初始学习率(learning rate)为0.003. 采用随机遍历算法确保训练集中的每一张图像都可被学习到, 每次处理256张图像, 最大迭代轮数(epochs)为500. 开展实验的软硬件环境如表2所示.
| 表 2 实验环境的配置参数 |
3 训练集和测试集上的拟合情况
LNet在训练集和测试集上accuracy和loss的拟合曲线分别如图5和图6所示. 可知拟合状况良好.

|
图 5 训练集和测试集上的accuracy曲线 |

|
图 6 训练集和测试集上的loss曲线 |
4 对比实验结果及分析 4.1 图像预处理模块
为验证本文设计的复杂验证码识别模型的优越性, 设计了本文模型与基于VGG16设计的模型A、基于ResNet-18设计的模型B、基于GoogLeNet设计的模型C和基于生成对抗网络(Generative Adversarial Networks, GAN)设计的模型D的对比实验. 实验在相同的实验环境下展开, 使用相同的训练集训练模型. 5种模型在IDB1、IDB2和IDB3测试集上的实验结果如表3和表4所示.
综合表3和表4可知, 本文设计的验证码识别模型除了在IDB2上的识别成功率小于基于GAN设计的方法外, 综合性能较其余4种模型均有着一定优势.
| 表 3 5种模型识别成功率(%) |
| 表 4 5种模型的识别平均时间(单位: s) |
4.2 消融实验
为说明本文在设计轻量神经网络时采用的策略对模型性能的影响, 设计了空洞卷积、1×1卷积核和多尺度稀疏结构在IDB1主数据库上的消融实验: 针对空洞卷积, 将LNet中用于验证码图像特征提取的卷积层改用尺寸为3×3的普通卷积核, 验证增大感受野对模型性能的影响; 针对1×1卷积, 删除所有用于降维的1×1卷积层, 查看其对参数数量的影响; 针对多尺度稀疏网络结构, 将其更换为如图7(b)所示的传统结构. 采用参数数量和识别率两项指标评估模型性能, 实验结果如表5所示. 参数数量的计算方法[20,21]可用式(13)表示.
| $ Parameters \leftarrow \sum\limits_i^D {K_{il}^2} \cdot {C_{iI}} \cdot {C_{iO}} $ | (13) |
其中, D是神经网络的层数, i表示第i个卷积层, kil表示第i个卷积层卷积核的边长, CiI表示输入第i个卷积层的通道数, CiO表示第i个卷积层输出的通道数. 模型的参数数量直接影响算法的时间复杂度和空间复杂度, 时间复杂度则决定了模型的训练和预测时间.

|
图 7 多尺度稀疏结构和传统结构 |
| 表 5 消融实验: 设计策略对模型性能的影响 |
由表5可看出, 引入空洞卷积后, 网络在不增加参数量的前提下提高了2.3%的性能; 1×1卷积的使用不仅提高了模型的识别率, 还将参数量减少了40.1%; 多尺度稀疏网络结构的使用, 也对模型性能的提升大有裨益.
5 结束语面向带彩色图形噪声、字符扭曲粘连的复杂验证码图像的识别任务, 本文融合了空洞卷积、1×1卷积以及多尺度稀疏网络结构的优点, 设计了名为LNet的轻量神经网络模型. 在相同的实验环境下使用相同的训练集证明了本文设计的复杂验证码识别模型的优越性和有效性; 设计消融实验展示了不同设计策略对模型性能的影响, 证明了本文设计模型的合理性. 值得进一步讨论的还有深度可分离卷积、可变形卷积[22]等对图像特征提取能力和模型参数数量的影响. 同时, 如何进一步地压缩模型以及如何利用现场可编程门阵列(Field Programmable Gate Array, FPGA)加速不同的卷积操作, 也是我们团队所关注的问题.
6 致谢本文工作受国家自然科学基金、湖北省教育厅科研计划及国家级大学生创新创业训练计划资助, 谨在此对提供基金支持的各位老师致以崇高的敬意; 对为本文实验设计做邮件指导的浙江大学蔡登教授和为实验开展提供必要环境的中国科学院武汉水生生物研究所王莹博士致以由衷的感谢.
| [1] |
Bursztein E, Martin M, Mitchell J. Text-based CAPTCHA strengths and weaknesses. Proceedings of the 18th ACM Conference on Computer and Communications Security. Chicago, IL, USA. 2011. 125–138.
|
| [2] |
Suykens JAK, Vandewalle J. Least squares support vector machine classifiers. Neural Processing Letters, 1999, 9(3): 293. DOI:10.1023/A:1018628609742 |
| [3] |
Avidan S. Support vector tracking. Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2001. Kauai, HI, USA. 2001.
|
| [4] |
LeCun Y, Jackel L, Bottou L, et al. Comparison of learning algorithms for handwritten digit recognition. International Conference on Artificial Neural Networks. Paris, France. 1995. 53–60.
|
| [5] |
Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Proceedings of the 25th International Conference on Neural Information Processing Systems. Red Hook, NY, USA. 2012. 1097–1105.
|
| [6] |
Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. https://arxiv.org/abs/1409.1556. [2014-09-04].
|
| [7] |
Szegedy C, Liu W, Jia YQ, et al. Going deeper with convolutions. Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Boston, MA, USA. 2015. 1–9.
|
| [8] |
Hu M, Yang SY. Overview of image mining research. 2010 5th International Conference on Computer Science & Education. Hefei, China. 2010. 1868–1870.
|
| [9] |
Fridrich J, Goljan M, Du R. Detecting LSB steganography in color, and gray-scale images. IEEE Multimedia, 2001, 8(4): 22-28. DOI:10.1109/93.959097 |
| [10] |
Ma NN, Zhang XY, Zheng HT, et al. ShuffleNet V2: Practical guidelines for efficient CNN architecture design. Proceedings of the 15th European Conference on Computer Vision (ECCV) 2018. Munich, Germany. 2018. 122–138.
|
| [11] |
Chen LC, Papandreou G, Kokkinos I, et al. DeepLab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(4): 834-848. DOI:10.1109/tpami.2017.2699184 |
| [12] |
Chollet F. Xception: Deep learning with depthwise separable convolutions. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu, HI, USA. 2017. 1800–1807.
|
| [13] |
Xu B, Wang NY, Chen TQ, et al. Empirical evaluation of rectified activations in convolutional network. https://arxiv.org/abs/1505.00853. [2015-05-05].
|
| [14] |
Liu LY, Jiang HM, He PC, et al. On the variance of the adaptive learning rate and beyond. https://arxiv.org/abs/1908.03265?context=cs. [2019-08-08].
|
| [15] |
Stooke A, Abbeel P. Accelerated methods for deep reinforcement learning. https://arxiv.org/abs/1803.02811. [2018-03-07].
|
| [16] |
Wang SL, Suo SM, Ma WC, et al. Deep parametric continuous convolutional neural networks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, UT, USA. 2018. 2589–2597.
|
| [17] |
杨观赐, 杨静, 李少波, 等. 基于Dopout与ADAM优化器的改进CNN算法. 华中科技大学学报(自然科学版), 2018, 46(7): 122-127. DOI:10.13245/j.hust.180723 |
| [18] |
Ruder S. An overview of gradient descent optimization algorithms. https://arxiv.org/abs/1609.04747. [2016-09-15].
|
| [19] |
Guyon I. A scaling law for the validation-set training-set size ratio. AT & T Bell Laboratories, 1997: 1.
|
| [20] |
Bergstra J, Bengio Y. Random search for hyper-parameter optimization. Journal of Machine Learning Research, 2012, 13: 281-305. |
| [21] |
唐玮, 赵保军, 龙腾. 基于轻量化网络的光学遥感图像飞机目标检测. 信号处理, 2019, 35(5): 768-774. DOI:10.16798/j.issn.1003-0530.2019.05.005 |
| [22] |
Dai JF, Qi HZ, Xiong YW, et al. Deformable convolutional networks. Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV). Venice, Italy. 2017. 764–773.
|
 2021, Vol. 30
2021, Vol. 30


