相比于传统的端到端通信协议无法适应多跳、消息延时、网络中断等特点, 机会网络[1,2] (Opportunistic Networks, OppNets)可更好的适应在特定极端网络环境下的通信问题. 机会网络是容忍延迟网络[3](Delay Tolerant Network, DTN)和移动自组网(Mobile Ad-hoc NETwork, MANET)下派生的网络, 是一种在网络延时或中断条件下也能以不同的方式自组网的网络. 不同于传统的无线网络, 它的节点位置和传输路径事先无法预知, 是利用节点间移动形成的可通信的机会来实现消息之间的传输,所以形成了它特定的存储-携带-转发路由模式. 机会网络越来越多的应用在军事、车联网[4] (Vehicular Ad-hoc NETworks, VANET)等网络环境和实际环境变化莫测的领域中, 极大地推进未来网络通信的智能化与高效化发展.
虽然机会网络的优势很突出, 但正是因为其特有的传输方式, 导致了信息在传输过程中可能会出现的诸多不确定性. 因而为了保证节点在传输过程中不易被恶意侵袭并保持相互良好的信任关系, 构建一个可信的路由模型是解决上述问题的基石.
目前, 越来越多的学者正在对机会网络中的可信路由模型进行研究和完善. 吴军等[5]提出一种基于反馈可信度的可信机会路由转发模型, 结合机会网络中的路由模型, 防止共谋节点加入机会路由转发候选集. 张玲玲等[6]提出了一种WMNs机会路由下弱可信节点共存机制, 在保证网络安全的前提下, 对无线 Mesh网络机会路由下弱可信节点的共存问题进行研究, 提出一种基于举报机制和马尔科夫预测的弱可信节点共存机制. 张光华等[7]提出一种基于博弈论的机会可信路由模型, 杨震等[8]提出另一种基于博弈论的机会可信路由模型, 该协议中, 选择下一条的最佳策略依赖于非零和合作博弈技术, 且考虑上下文信息与相应节点到目的地的距离作为博弈的重要属性. 樊娜等[9]通过建立一种基于不确定性理论的节点信誉度混合评估模型, 对信息源节点的可信程度进行评估, 结合信息源节点的信誉度, 建立车辆节点行为可信决策机制. Mahdi等[10] 提出一种基于FPGA的神经网络在室内环境下利用WSN精确估计老年人跌倒的距离, 用来保障老年人的独居生活. 未来的车联网信任体制, 会越来越完善, 恶意行为会随着网络信任体系的加强逐渐减少, 可信路由模型也将更好的应用于机会网络等复杂多变的网络.
本文将通过建立一种基于反馈节点可信度的信任评估模型(Trust Evaluation model based on FeedBack node trust, TE-FB), 并把该信任评估模型与经典机会路由算法[11-13]中的Spray and Focus算法相结合提出一种基于反馈节点信任度的可信路由算法, 记为FB-SF模型. 通过直接信任度和间接信任度的融合计算得出一个最终信任度, 即为网络中任意一节点在交互时的信任度大小, 并依据此来判断该节点是否可信. 直接信任度采用传统的贝叶斯概率理论, 间接信任度利用节点间的反馈机制得出, 最终的信任度合成则采用最简单的加权分配计算模式以尽可能的降低能耗.
1 信任模型信任模型[14-16]的核心作用就是要让模型适应特定的实际环境, 在本文研究的车联网环境中, 信任模型的作用就是尽可能大的规避恶意节点对网络中的可信节点带来的攻击而导致车联网信息数据传输的不准确性. 计算节点的信任度, 不仅要靠直接信任度还要靠间接信任度. 信任模型的主要部分包括信任度计算, 信任度和成及信任度更新3部分.
1.1 直接信任直接信任度DTmn根据传统的贝叶斯先验分布特征, 对未知节点的行为与节点的历史交互记录进行结合考虑, 得出一个节点后续可能出现的概率分布情况, 以此为依据对节点后续的传输行为做出预判. 在车联网中, 首先假设车辆节点m, n之间的交互行为是随机产生且互不影响的, 彼此相互独立, 则每次交互事件独立同分布. 定义其中两节点交互总次数为N(成功交互Nc次, 失败交互Nf次), 交互成功的概率为p, 则节点m, n满足二项分布:
| $p\left( {\frac{{{N_c}}}{p},N} \right) = \left( \begin{array}{l} N \\ {N_c} \\ \end{array} \right){p^{{N_c}}}{\left( {1 - p} \right)^{{N_f}}}$ | (1) |
其中, 0 ≤ p ≤ 1, N为时间T内的交互次数统计, T为一个预设的时钟. N ≥ 0, Nc ≥ 0, Nf ≥ 0. 利用分布函数估计事件发生的可信度, 函数为连续函数.
贝叶斯中的各节点初始状态未有过交互行为, 在[0, 1]上满足均匀分布, 即可用贝叶斯求交互成功的后验概率. 成功交互次数 Nc与p满足:
| $h\left( {{N_c},p} \right) = \left( \begin{array}{l} N \\ {N_c} \\ \end{array} \right){p^{{N_c}}}{\left( {1 - p} \right)^{{N_f}}}$ | (2) |
交互成功的后验分布为:
| $\pi \left( {\frac{p}{{{N_c}}}} \right) = \frac{{\Gamma \left( {N + 2} \right)}}{{\Gamma \left( {{N_c} + 1} \right)\Gamma \left( {{N_f} + 1} \right)}}{p^{{N_c}}}{\left( {1 - p} \right)^{{N_f}}}$ | (3) |
后验概率期望为:
| ${\mathop {{p}}\limits^ \wedge}_{B} = D{T_{mn}} = E\left( {\beta \left( {{N_c} + 1,{N_f} + 1} \right)} \right) = \frac{{{N_c} + 1}}{{N + 2}}$ | (4) |
由上述结果可知, 节点的交互成功率与节点的可信度成正比.
1.2 间接信任间接信任ITmn是利用可提供反馈信息的节点传递给预设节点的反馈值可靠度来判断节点信任度的, 与直接信任度类似, 高反馈值节点将具有高的信任度与高的相对占比. 通常情况下, 交互越频繁的节点之间反馈信息可信度越高. 定义节点交互频繁度IFmn为:
| $I{F_{mn}} = \frac{s}{t} \times {\beta ^{\textstyle\frac{1}{s}}},\;\beta \in \left( {0,\;1} \right) \cap s \ne 0$ | (5) |
其中, s代表节点m, n交互的次数, t代表m节点与周围其他节点的交互次数. 其中其他节点范围定义为以节点m, n连线为直径的圆内任意节点. β是IFmn的平衡系数, 根据经验多取值在0.4~0.7之间.
频繁的交互就可能导致相似节点出现的概率越大, 节点之间相似程度趋于稳定一致. 定义节点相似程度SImn为:
| $S{I_{mn}} = \left\{ \begin{array}{l} S{I_{mn}} + \dfrac{{1{\rm{ - }}S{I_{mn}}}}{2} \times \left( {1{\rm{ - }}\dfrac{{C{D_{mn}}}}{p}} \right),\;C{D_{mn}} < a \\ S{I_{mn}} - \dfrac{{S{I_{mn}}}}{2} \times \left( {1 - \dfrac{p}{{C{D_{mn}}}}} \right),\;C{D_{mn}} \ge a \\ \end{array} \right.$ | (6) |
其中, CDmn表示两节点共同交易过后对某个节点的评价差值, 其中共同交易过的节点集合也是以节点m, n连线为直径的圆内任意节点. a 为两节点可接受的相对最大评价误差, 误差来自于所有节点历史交互中评价值最高节点与最低节点的相对误差.
综上, 间接信任可表示为:
| $I{T_{mn}} = I{F_{mn}} \times S{I_{mn}}$ | (7) |
由上述结果可知, 节点的交互频繁度和相似程度都与节点的反馈信任度成正比.
1.3 信任度和成机会网络中, 信任合成采用最简单的带权求和以尽可能降低能耗, 故任意节点的综合信任Tmn定义为:
| ${T_{mn}} = \eta I{T_{mn}} + \left( {1 - \eta } \right)D{T_{mn}}$ | (8) |
其中, 0<η <1. 通常情况下 η 是一个大概率事件, 即相比于别的节点, 信任自己是相当容易的. 当η为0时, 信任度只与间接信任有关; 当η为1时, 信任度只与间接信任有关.
1.4 信任更新综合信任度的大小决定该节点是否能继续与下一个节点进行交互. 若综合信任度满足某一阈值, 则表示交互成功的列表更新一次; 若综合信任度不满足阈值, 那么不进行交互, 则表示其他的列表更新一次. 信任表更新如下:
| ${{Table}_{\rm new}} = \left\{ \begin{array}{l} Tabl{e_{\rm old}}\left( {succeed} \right) + 1 \\ Tabl{e_{\rm old}}\left( {other} \right) + 1 \\ \end{array} \right.$ | (9) |
其中, Tablenew表示的是更新后的信任列表, Tableold表示的是未更新的信任列表.
2 FB-SF模型可信机会路由实现方法主要包括节点的转发机制,对待转发的节点进行信任判断, 安全选择下一跳并进行转发, 最终消息传达到目的节点.
2.1 可信路由转发机制在机会网络中, 由于传输模式的不确定性, 如何判断节点的可信度是转发成功的关键.
第1步. 节点初始化: 系统产生M个模拟车辆节点, 都为非空的消息节点, 当携带源数据的节点在遇到第一个其他节点时, 利用信任评估模型判断这个节点是否可信. 具体计算可由综合信任度表达式一步一步获得, 具体过程如下. 经过多次交易以后, 正常节点可以在每次交互后获得一定的信任值, 累加之后可在一段时间内获得较高的信任度, 而且其他节点对其相似程度评价趋于稳定一致性, 优先被选为可信转发节点, 并判断为可信节点. 而恶意节点在间接信任中因为交互次数受限和节点间相似度不稳定不一致导致信任度较低, 在一段时间内或被抵制清除. 判断两个节点若都为可信节点, 那么这两个节点进行交互; 若不可信, 则初步判断为恶意节点. 则不进行数据转发, 继续在范围内寻找可信节点.
第2步. 节点复制策略: 被判断可信的节点之间采用基于二分法的复制策略, 可达到高效转发. 具体来说就是第一次复制后, 拥有副本的可信节点在遇到新的可信节点时都将自己的一半副本分给新的节点, 直到拥有副本的可信节点达到一定的数目, 且所有的可信节点中只保留剩余一个消息副本, 复制结束.
第3步. 等待中继节点: 若副本在复制阶段没有发现目的节点, 则每个携带副本的可信节点采用一种基于单复制的路由策略, 等待效用较高的中继节点将消息传给目的节点. 具体的来说就是消息根据预先设定的标准来转发到不同的中继, 这样可以避免节点在遇到新的节点后进行盲目转发而导致网络资源的浪费. 整个转发机制如图1所示. 如果要选择更高效的中继节点, 则延迟将增加.
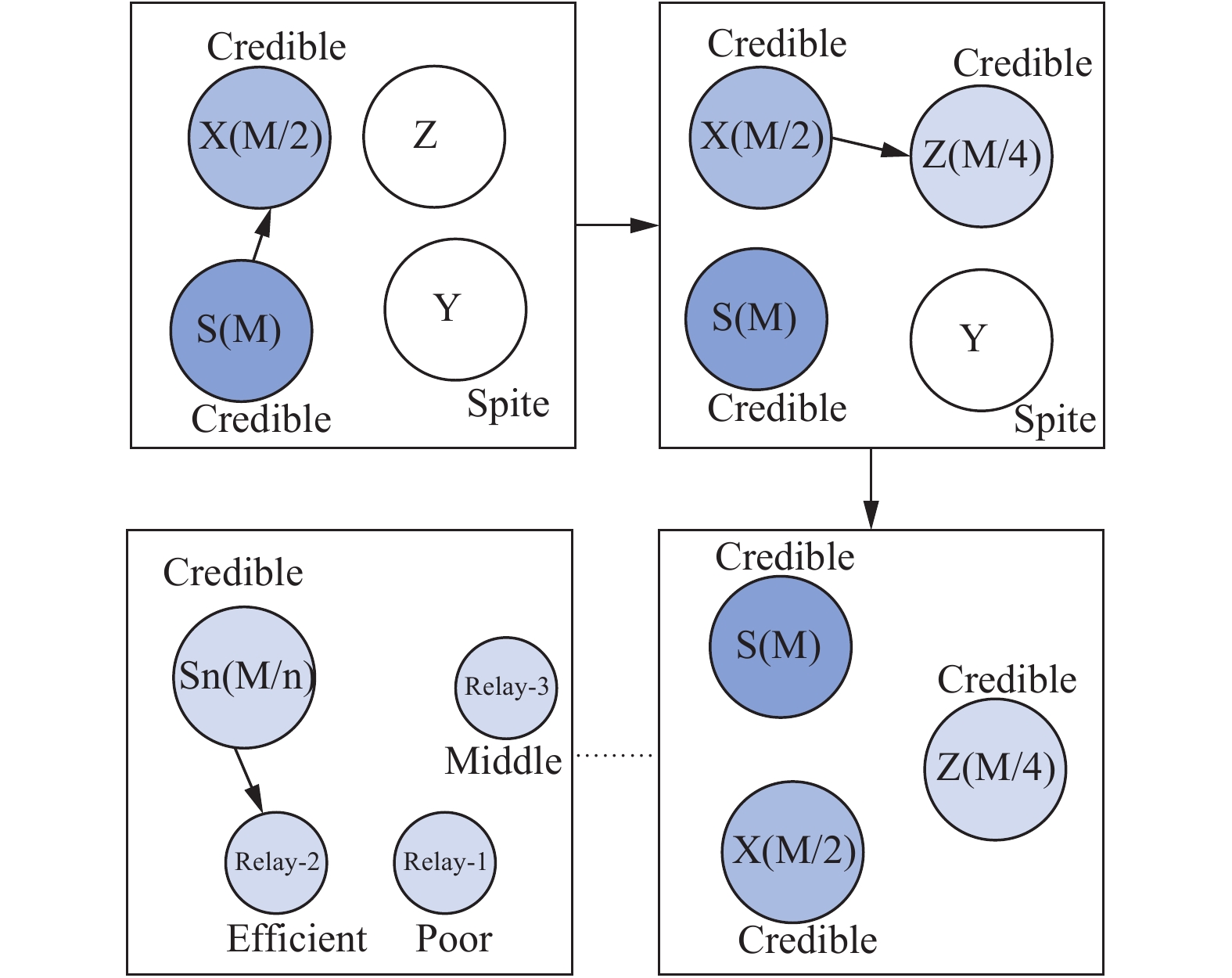
|
图 1 机会路由转发机制示意图 |
2.2 相关算法伪代码 2.2.1 路由转发机制
路由转发机制的伪代码如代码1所示.
代码1. 路由转发策略
输入: nrofCopies
输出: copiesLeft.size
Start
Math.ceil
Massage ← messageTransferred(id,from)
if (isBinary)
//receiving node gets ceil(n/2) copies
nrofCopies ← nrofCopies/2.0
else
//receiving node gets only single copy
nrofCopies ← 1
return Massage
//Create a list of message replicas
if (copiesLeft.size() > 0)
Timer = 0
getConnections ← copiesLeft
//Get a list of message copies
if (nrofCopies > 1 && nrofCopies= nrofRelay)
copiesLeft.size++
Timer = Timer + 12
else
return copiesLeft.size
//Reduce the number of legacy message copies
if (0 < Timer < 12)
endCopies ← nrofCopies /2.0
nrofCopies – –
2.2.2 信任度计算与更新信任度计算与更新过程如代码2所示.
代码2. 信任度计算与更新
输入: copiesLeft.size, node m, node n, Tableold, Trust threshold x
输出: DTmn,ITmn, Tmn, Tablenew, Node interaction
Start
copiesLeft.size(m,n) ← 0
if m=n
return
else
copiesLeft.size(m,n) update
//Calculated confidence
根据式(4), 式(7), 式(8)计算DTmn,ITmn and Tmn
//Trust update
根据式(9)更新Tablenew
if (Tableold
Tablenew
else
return
3 仿真实验 3.1 仿真工具本研究使用ONE (Opportunistic Network Environment simulator)[17,18]仿真工具, 模拟出一种智能交通系统, 分析了不同算法的3个性能指标, 即平均传输延时、成功投递率和恶意节点检测率, 比较了FB-SF模型和经典路由算法基于不同预设值的优缺点. 具体节点的仿真数据为默认配置. 如表1所示.
| 表 1 默认参数设置 |
车辆移动模型有随机移动模型(Random Way Movement, RWM), 基于巴士的移动模型(Bus Movement, BM), 基于地图的移动模型(Map Based Movement, MBM), 基于地图路由的移动模型(Map Route Movement, MRM)和基于最短路径的移动模型(Short Path Movement, SPMB). 各移动模型的简介如表2所示.
为能模拟出更加真实的车辆行驶环境, 我们选择其中实用性最强且算法高效的SPMB移动模型作为仿真的默认移动模型.
| 表 2 移动模型及简介 |
3.2 模型相关参数评估 3.2.1 参数s占比
节点交互频繁度的计算中, 参数s代表的是节点m与最邻近节点 n交互的次数, 不同占比的s可能导致不同的交互频繁度. 不同的s占比与相应节点交互频繁度关系如图2所示.
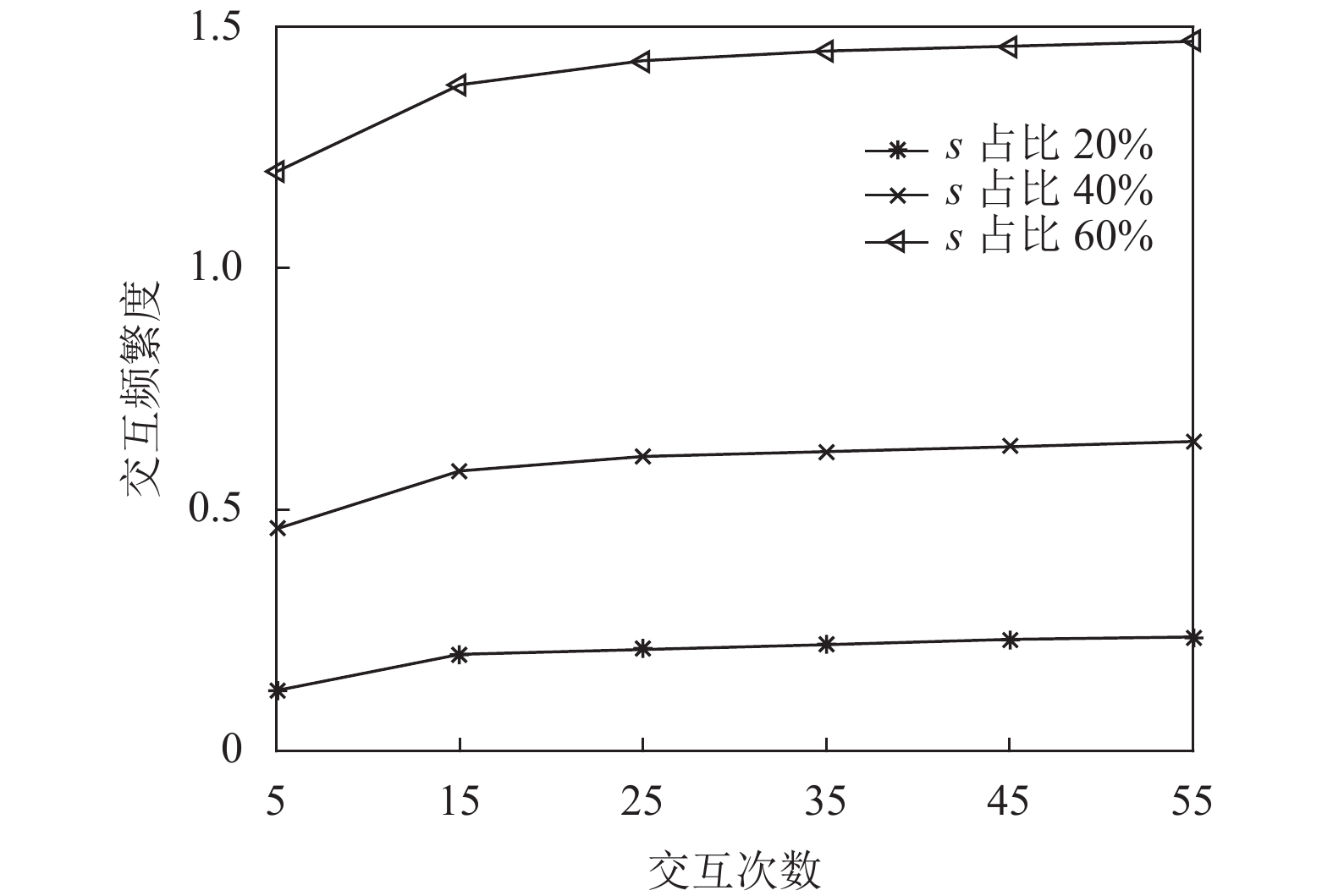
|
图 2 参数s占比与节点交互频繁度关系 |
3.2.2 误差交易评价
在节点相似度计算中, 两节点共同交易后对某节点评价可接受的最大误差a影响着不同节点的节点相似度. 不同的a值对节点的节点间相似度影响程度如图3所示.
由图2可得, 当m节点与最邻节点n交互的次数越来越多时, 交互频繁度就越来越高, 是因为当m节点与圆周范围内的节点交互时, 可能会有更多的自私节点或者恶意节点的存在导致节点交互失败, 交互频繁度降低. 因此, 选择高占比的s值可使节点交互更频繁, 节点间历史交易记录更多, 节点可信度就越大. 由图3可得, 随着误差评价增大, 历史交互节点数量增加, 正常节点没有不良历史记录和高的反馈值所以节点相似度逐渐趋于高稳定, 恶意节点分为两类可能出现的情况. A类恶意节点之前有过交互行为, 由于低的反馈值在出现短暂时间后相似度下降并趋于低稳定, B类恶意节点由于还没有交互行为, 所以在出现前期相似度不稳定, 但之后会因为低反馈值而使相似度持续降低最终达到低稳定. 但是正常节点的节点相似度一直高于恶意节点, 相似度越高, 节点信任值越高. 因此, 选择范围内尽可能大的评价误差可以有效排除恶意节点.

|
图 3 a值与节点的节点间相似度关系 |
3.3 性能指标 3.3.1 平均传输延时
传输延时是分组数据从源节点到达目的节点的时长, 常采用平均传输延时评价路由性能. 在机会网络中, 高延时被被允许存在, 但减小延时可以更好的提高资源的复用率和网络工作的效率. 3种算法的传输延时对比如图4所示.
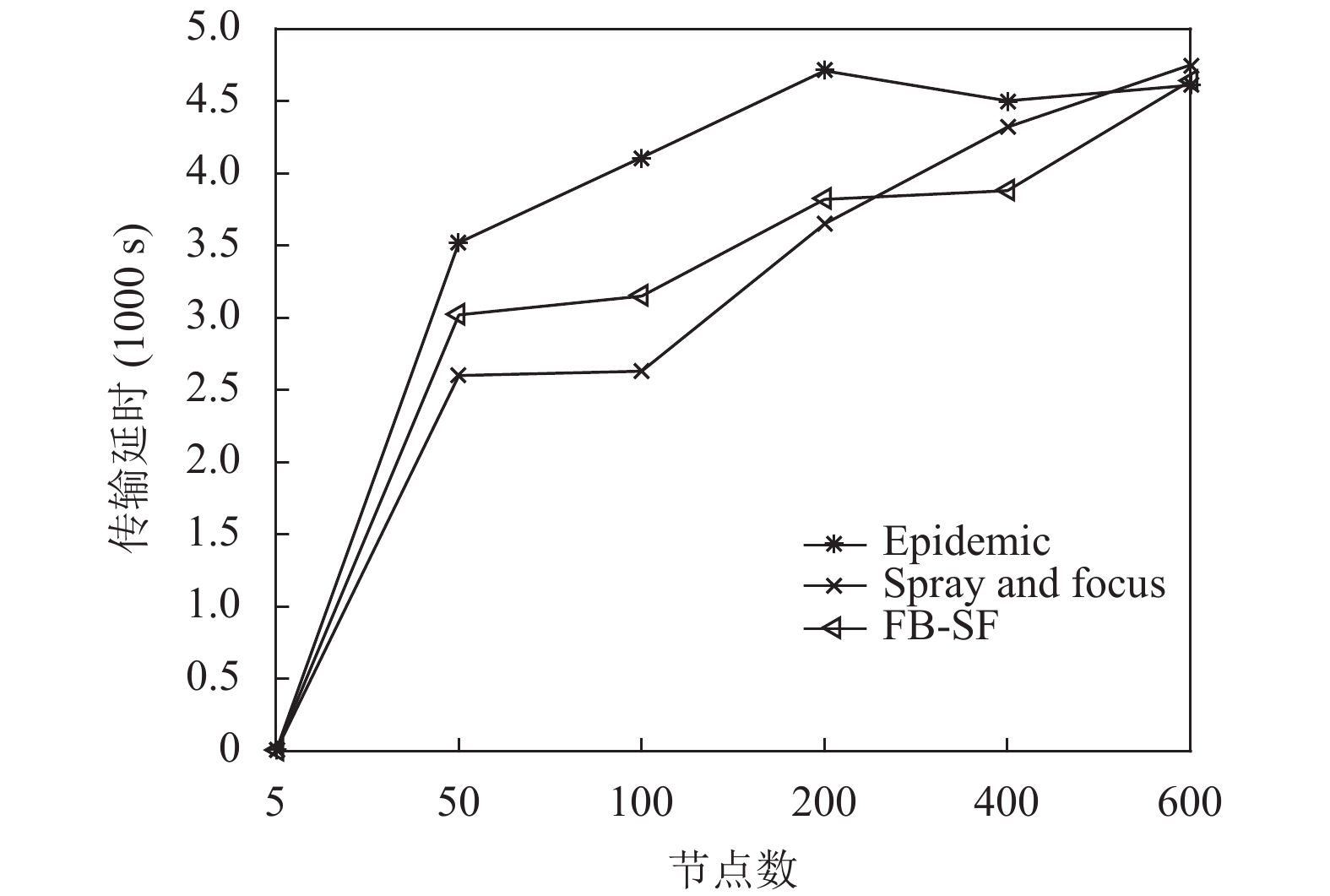
|
图 4 3种算法延时对比 |
3.3.2 成功投递率
成功投递率是指在规定的时间内成功接收的数据分组数占发送数据总量的比例. 比例越高说明数据的传输效率越高. 成功投递率是确定路由模型是否能正确投递相应分组据的重要指标. 3种算法的成功投递率对比如图5所示.

|
图 5 3种算法成功投递率对比 |
3.3.3 恶意节点检测率
恶意节点检测率是指一定量的正常节点数下, 路由所能检测的恶意节点数量占正常节点数的百分比. 此性能的检测依赖于仿真的运行时间和正常节点数目. 3种算法的恶意节点检测率对比如图6所示.
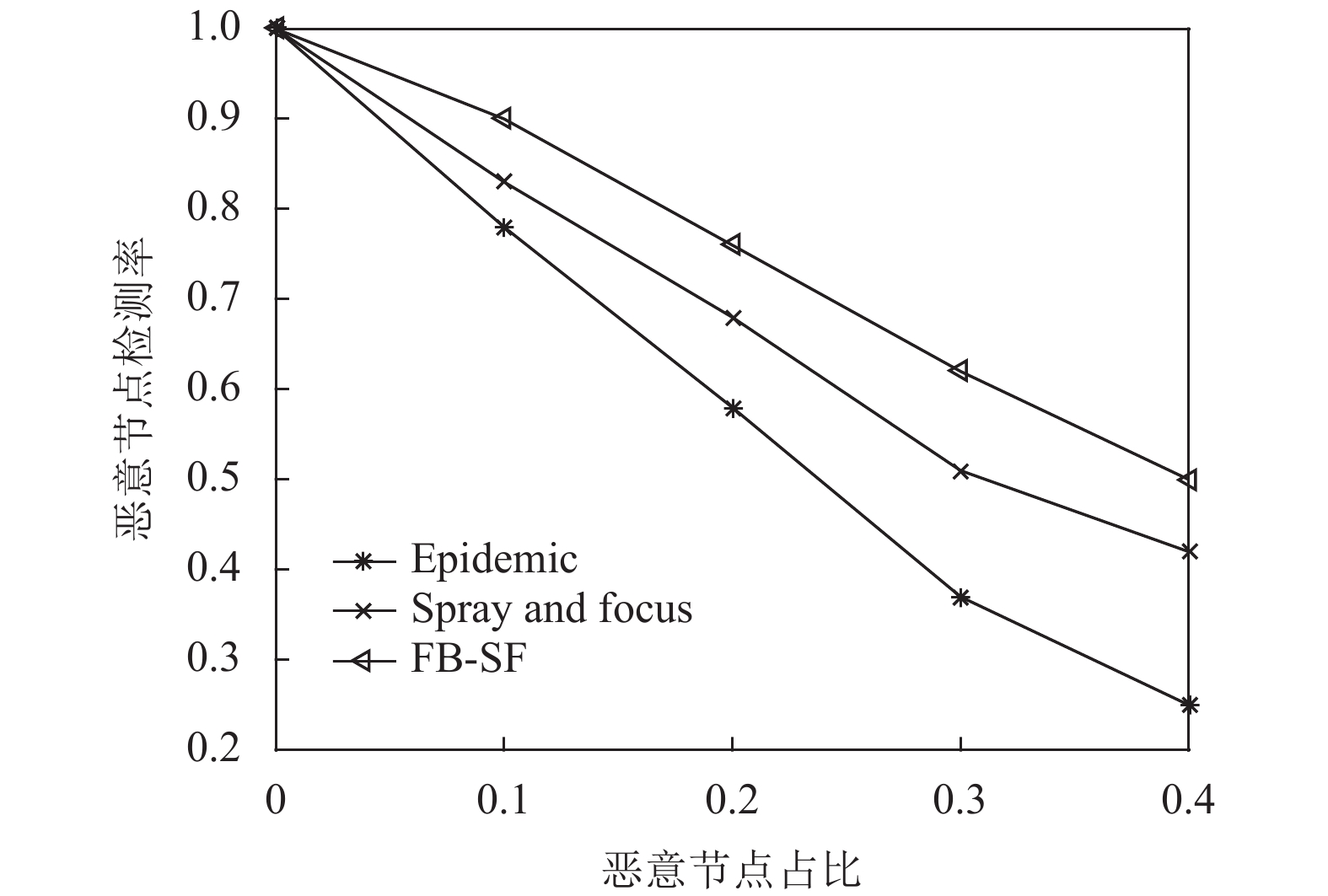
|
图 6 3种算法恶意节点检测率对比 |
4 仿真结果分析
由图4可知, 当车辆数大于50时, 各算法的传输延时开始出现明显不同. Epdemic算法由于泛洪机制而造成较大的延时, FB-SF模型在车辆数超过350时由于大量计算信任值而造成相应延时, 但总体来说延时在可控范围内. 车辆数达到饱和时, FB-SF模型比Epdemic算法的延时仅高约4%.
由图5可以看出, 3种算法的成功投递率在车辆数小于50时并无明显差别, 当车辆数大于100时. Epdemic算法的成功投递率稳定在0.145左右, 其他2个算法的投递成功率逐次上升. 当车辆数接近饱和时, FB-SF模型成功投递率比Spray and Focus算法提高了约4.6%并逐渐保持稳定.
由图6可得, 随着恶意节点占比越来越大, 各算法的检测率也依次下降. FB-SF模型在面对恶意节点入侵时性能优于Epdemic和Spray and Focus. FB-SF模型增加了节点间反馈可信度与节点综合信任度的度量, 使节点间的信任权重分配更加合理, 从而可以对恶意攻击进行有效检测.
5 结论与展望本文在ONE仿真平台上实现了对两种经典路由算法和FB-SF模型在不同车辆节点数下的成功投递率、传输延时和特定环境下恶意节点检测率三个指标进行研究与性能对比. 研究结果表明: 不同预设值对各路由算法均会产生不同程度的影响. FB-SF模型在抑制恶意入侵方面有良好的表现, 对车联网安全维护和车载数据传输提供了路由保障. 但是缺陷还是有的, 比如没有考虑信任模型与其他经典算法融合的效果. 在今后的工作中, 将把信任评估模型加在更多的路由算法中来对比同一个评估模型对不同机会路由的影响, 结合车联现状和发展前景, 提出更优的信任模型来应对更复杂的网络环境, 保障用户和车载信息安全.
| [1] |
王桐, 单欣, 郑欣蕊. 一种基于轨迹预测的机会网络路由协议. 应用科技, 2020, 47(3): 94-99. |
| [2] |
孙践知. 机会网络路由算法. 北京: 人民邮电出版社, 2013.1–2.
|
| [3] |
Qi YW, Yang L, Pan CS, et al. CGR-QV: A virtual topology DTN routing algorithm based on queue scheduling. China Communications, 2020, 17(7): 113-123. DOI:10.23919/J.CC.2020.07.010 |
| [4] |
周映, 张月霞. 5G环境下车联网跟驰模型. 计算机应用研究, 2021, 38(2). http://www.arocmag.com/article/02-2021-02-057.html
|
| [5] |
吴军, 莫伟伟, 印新棋, 等. 基于反馈可信度的可信机会路由转发模型. 计算机工程与应用, 2017, 53(8): 23-28. DOI:10.3778/j.issn.1002-8331.1611-0091 |
| [6] |
张玲玲, 吴军, 印新棋, 等. WMNs机会路由下弱可信节点共存机制. 计算机工程与设计, 2019, 40(10): 2757-2764. |
| [7] |
张光华, 庞少博, 杨耀红, 等. 机会网络中基于博弈论的可信路由模型. 华中科技大学学报(自然科学版), 2018, 46(1): 11-16. |
| [8] |
杨震, 赵丽. 机会网络中利用博弈论的可信路由协议. 重庆理工大学学报(自然科学), 2019, 33(6): 190-198. |
| [9] |
樊娜, 段宗涛, 王青龙, 等. 面向车联网环境的车辆行为可信决策机制. 计算机工程与设计, 2018, 39(1): 33-37, 43. |
| [10] |
Mahdi SQ, Gharghan SK, Hasan MA. FPGA-Based neural network for accurate distance estimation of elderly falls using WSN in an indoor environment. Measurement, 2021, 167: 108276. DOI:10.1016/j.measurement.2020.108276 |
| [11] |
何志立, 潘达儒, 宋晖. 一种基于聚类算法的机会网络路由算法. 华南师范大学学报(自然科学版), 2019, 51(4): 120-128. |
| [12] |
姚明辉, 张胜, 王瑜, 等. 机会网络中基于社团的能量均衡路由算法. 小型微型计算机系统, 2018, 39(9): 1914-1920. DOI:10.3969/j.issn.1000-1220.2018.09.005 |
| [13] |
王雪丽, 张琳娟, 张迪. 车载传感网中基于群特性的MaxProp路由协议改进. 计算机应用与软件, 2017, 34(5): 255-260, 298. DOI:10.3969/j.issn.1000-386x.2017.05.044 |
| [14] |
张宇, 张妍. 零信任研究综述. 信息安全研究, 2020, 6(7): 608-614. DOI:10.3969/j.issn.2096-1057.2020.07.006 |
| [15] |
朱研, 张辉. 关于无线自组网的分簇信任安全路由研究仿真. 计算机仿真, 2020, 37(6): 310-313. DOI:10.3969/j.issn.1006-9348.2020.06.063 |
| [16] |
曾红玉. 网络安全模型与零信任的实践探讨. 计算机产品与流通, 2020(7): 48. |
| [17] |
Mass J, Srirama SN, Chang C. STEP-ONE: Simulated testbed for Edge-Fog processes based on the Opportunistic Network Environment simulator. Journal of Systems and Software, 2020, 166: 110587. DOI:10.1016/j.jss.2020.110587 |
| [18] |
王文涛, 郑芳, 王奇枫, 等. 基于ONE平台的机会网络路由协议仿真分析. 中南民族大学学报(自然科学版), 2014, 33(3): 110-114. |
 2021, Vol. 30
2021, Vol. 30



