随着智能物联网(AIoT)的兴起, 人们对智能化服务的需求也越来越多. 无线传感网(WSN)作为AIoT的关键组成部分, 其运行状态, 直接影响AIoT的服务质量. 然而, WSN通常部署在环境恶略的地方. 员工无法对WSN中的所有节点进行24小时实时观察和检查. 但是, 一旦WSN中节点出现故障, 将直接影响系统最终的研判. 为此, 研究高效可靠的WSN节点故障诊断方法尤为重要, 它对延长WSN寿命, 保持系统稳定和提高系统服务质量具有重要的现实意义. 目前, WSN节点故障诊断方法可分为基于统计学原理、故障分类和感知数据的时空特性分析三大类. 常用的诊断算法, 如文献[1]采用2-回合投票故障诊断算法对故障进行诊断, 文献[2]以ICA进行故障属性的约简, 通过朴素贝叶斯进行故障诊断, 文献[3]利用WSN感知数据的时空相关性原理将诊断正常的候选簇头的观测值与簇内成员节点的观测值比较来对簇内成员节点进行诊断, 文献[4]以粗糙集进行故障属性的约简, 通过GA-KELM算法对对故障诊断. 这些方法要么存在故障属性约简不彻底, 要么算法模型的参数复杂等问题. 本文鉴于他们的研究经验, 提出一种基于RS-CSA-ELM的WSN节点故障诊断方法, 以RS对故障属性进行约简, 并以CSA优化EML参数作为故障诊断模型, 完成WSN节点故障诊断. 该算法仿真结果表明, 此法算法模型参数设置简单、易实现, 故障诊断的精确度高、误诊率低.
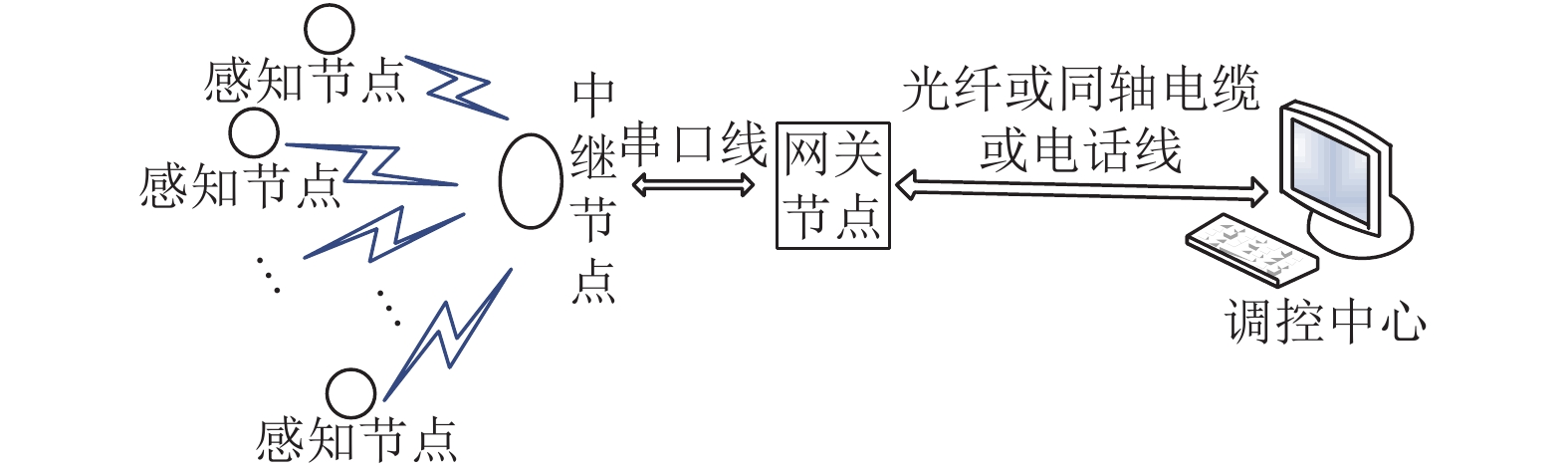
1 WSN节点故障分析 1.1 WSN网络结构WSN是一种高度自组织智能型数据处理网络, 通过节点的密集部署, 实现数据的量化收集、聚合和传输操作. 典型的WSN组成分为传感节点、中继节点、网关节点、调控中心4个部分. 其结构如图1所示.
1.2 WSN节点结构及故障分析WSN节点自身就是一个高内聚低耦合的结构化产品, 它由感知单元、处理单元、信息收发单元及能量保障单元, 其结构如图2所示. 这4个独立的单元相互协作完成节点的任务, 任何一个单元出现出现故障将导致最终数据的错误影响WSN的正常工作. 而每个单元都具有自己的特征, 因此查找节点故障等同于查找节点产生故障的功能单元. 这种检测方法精度高, 便于维修[5–7], 本文针对WSN网络结构及其节点结构, 将故障分为能量保障单元故障、处理单元故障、信息收发单元故障以及感知单元故障.
2 WSN节点故障诊断算法设计 2.1 故障诊断属性约简算法粗糙集理论属性约简算法(简称RS)能从模糊数据本身归纳出数据关键信息, 删除冗余信息, 求得最小表达式, 建立决策表. 正好可用于对WSN节点故障诊断属性的约简, 其过程如下: 设故障诊断决策表为
| $ {C_D}(i,j) = \left\{ \begin{array}{*{20}{l}} m[k],&d({x_i}) = d({x_j})\\ 0,&d({x_i}) \ne d({x_j}) \end{array}\right. $ |
其中,
|
图 1 典型WSN网络结构 |

|
图 2 WSN节点结构 |
基于上述分辨矩阵的故障属性约简算法步骤如下:
(1)利用上文描述, 根据故障样本决策表构建分辨矩阵
(2)约简分辨矩阵
(3)若
| $T = \mathop \wedge \limits_{{C_D}(i,j) \ne \emptyset } \{ \mathop \vee \limits_{m[k] \in {C_D}(i,j)} m[k]\} $ |
(4)向步骤(3)的RS属性样本T中每一项都添加步骤(2)中的单属性, RS属性样本约简T', 其每项都代表一个故障属性约简.
2.2 WSN节点故障诊模型RS-CSA-ELM算法对故障诊断原理描述为: 以WSN节点故障预兆构建故障样本数据集, 以故障种类属性和特征属性构建故障决策表. 首先, 根据RS剔除原始故障样本属性冗余信息, 获得约简后的故障属性组合; 其次, 利用属性之间的相关性选取最优属性约简; 以最优属性约简构建新的故障样本作为算法模型的训练样本, 最后, 建立RS-CSA-ELM故障诊断模型对WSN节点故障进行诊断, 如图3所示.

|
图 3 WSN节点的RS-CSA-ELM故障诊断模型 |
2.3 CSA-ELM算法
(1)极限学习机(ELM)原理
设给定N组WSM节点数据样本
| ${f_L}(x) = \sum\limits_{i = 1}^L {{\beta _i}G({\alpha _i} \cdot {x_j} + {\gamma _i})} = {t_i},j = 1,2, \cdots ,N$ |
其中,
| $H\beta = T$ |
其中,
| $ H = {\left[ {\begin{array}{*{20}{c}} {G({\alpha _1} \cdot {x_1} + {\gamma _1})}& \cdots &{G({\alpha _L} \cdot {x_j} + {\gamma _L})}\\ \vdots & \ddots & \vdots \\ {G({\alpha _1} \cdot {x_N} + {\gamma _1})}& \cdots &{G({\alpha _L} \cdot {x_N} + {\gamma _L})} \end{array}} \right]_{N \times L}} $ |
| $ \beta = {\left[ {\begin{array}{*{20}{c}} {\beta _1^T}\\ \vdots \\ {\beta _L^T} \end{array}} \right]_{L \times m}},\;T = {\left[ {\begin{array}{*{20}{c}} {t_1^T}\\ \vdots \\ {t_L^T} \end{array}} \right]_{N \times m}} $ |
当
(2) CSA优化ELM
极限学习机(ELM)是一类基于前馈神经网络的训练算法, 其具有学习速度快、泛化性能强、不易陷入局部极值的特性, 因此被广泛应用[9]; 但由于该算法中输入权值
乌鸦搜索算法(CSA)是仿效乌鸦在储备食物和盗窃食物的智能行为而形成的一种基于种群的优化算法, CSA与其它神经网络参数优化算法如GA、POS一样, 均是利用种群的优势来增加寻找最优解的概率, 同时避免陷入局部最优解. 但优化算法的参数设置对其性能影响很大, 所以参数越少的算法越易应用. 种群优化算法除种群大小和最大迭代次数外, 还要设置其它参数, 如GA还需再设置选择方法、交叉方法、交叉概率、变异方法以及变异概率; PSO还需再要设置有惯性权重、粒子自身的学习因子和社会学习因子; 而只需再设置乌鸦的飞行长度和辨识概率即可[11–13].
另外, CSA不是贪心算法, 如在搜索空间范围内只要没有比乌鸦产生的新位置更优, 它依然会飞向新位置, 这样产生的解是多样的, 使得算法具有最大概率寻找最优解功能. 乌鸦跟踪行为是随机的, 这样就增大了算法搜索空间, 即CSA具有全局搜索能力. 算法在迭代过程中, 种群中所有乌鸦都在不断地更新藏食地点, 从而保证种群中所有的藏食地点是最优的, 并利用乌鸦记忆记录最优存食位置. 迭代结束后, 找到种群中乌鸦的适应度值最优的记忆作为最后求到的最优解. 表1为CSA与GA和PSO算法的性能比较.
| 表 1 CSA与GA和PSO算法性能比较 |
CSA算法应用到ELM的输入权值

|
图 4 CSA-ELM算法流程 |
该算法的详细操作要领如下:
Step 1. 算法初始化. 确定ELM各层的神经元个数, 随机生成ELM的输入权值
Step 2. 计算乌鸦适应度. 适应度计算公式为:
| $f( \cdot ) = \frac{{{N_e}}}{N}$ |
其中, Ne为正确的样本数, N为训练样本总数.
Step 3. 更新乌鸦记忆. 更新的计算公式为:
| $ {m^{i,iter + 1}} = \left\{ {\begin{array}{*{20}{l}} {{x^{i,iter + 1}}},&{f\left( {{x^{i,iter + 1}}} \right)\;{\rm is\;better\;than\;}f\left( {{x^{i,iter}}} \right)}\\ {{m^{i,iter}}},&{o \cdot w} \end{array}} \right. $ |
检查终止条件, 若满足则输出最优的
Step 4. ELM训练和诊断. 将最终乌鸦位置和记忆作为最优的ELM的输入权值和阀值赋予ELM, 使用训练样本对ELM进行训练, 采用公式
根据上文所述, 将RS的故障属性约简算法与经CSA优化的极限学习机有机结合, 构建基于RS-CSA-ELM的WSN节点故障诊断算法, 其过程如下:
Step 1. 根据WSN节点组成结构, 构建符合实际情况的WSN节点故障属性表并做量化处理.
Step 2. 根据上文所提的故障属性约简算法对Step 1构建的WSN节点故障属性表进行属性约简, 删除冗余的故障属性信息, 得到最优的故障诊断决策表.
Step 3. 根据Step 2得到的故障属性决策表重构训练样本数据集.
Step 4. 将Step 3得到的训练样本数据集作为RS-CSA-ELM算法模型的输入, 利用CSA优化ELM的参数, 即利用训练的故障样本数据对ELM进行训练, 使其达到最佳的ELM故障模型, 而后用该模型对待诊样本数据进行故障诊断, 实现WSN节点故障任务.
3 仿真与结果分析 3.1 仿真实验设置(1) WSN节点故障属性的约简
为验证上述算法得有效性, 先构建其故障属性及量化表(表2), 再将表2转换为故障诊断决策表(表3). 最后采前文中设计的RS故障属性约简算法对表2进行约简, 以获得最优故障诊断决策.
| 表 2 部分故障属性及量化处理表 |
| 表 3 部分故障诊断决策表 |
(2)算法参数设置
仿真设置算法初始条件: 飞行长度
为验证所提算法的性能及可行性, 在Ubuntu16.04环境下用Python3.5+ Tensorflow编程仿真, 同时考虑到WSN实际工作环境, 实际所收集的数据参与真实数据之间存在误差. 模拟在同一条件下对优化前后EML性能进行仿真试验, 同时也对本文所提算法与最新文献所提算法作了对比仿真实验.
3.2 仿真结果分析首先, 在相同条件下, 对CSA优化前的ELM与优化后的ELM模型进行了对比测试, 其结果如图5、图6所示.
|
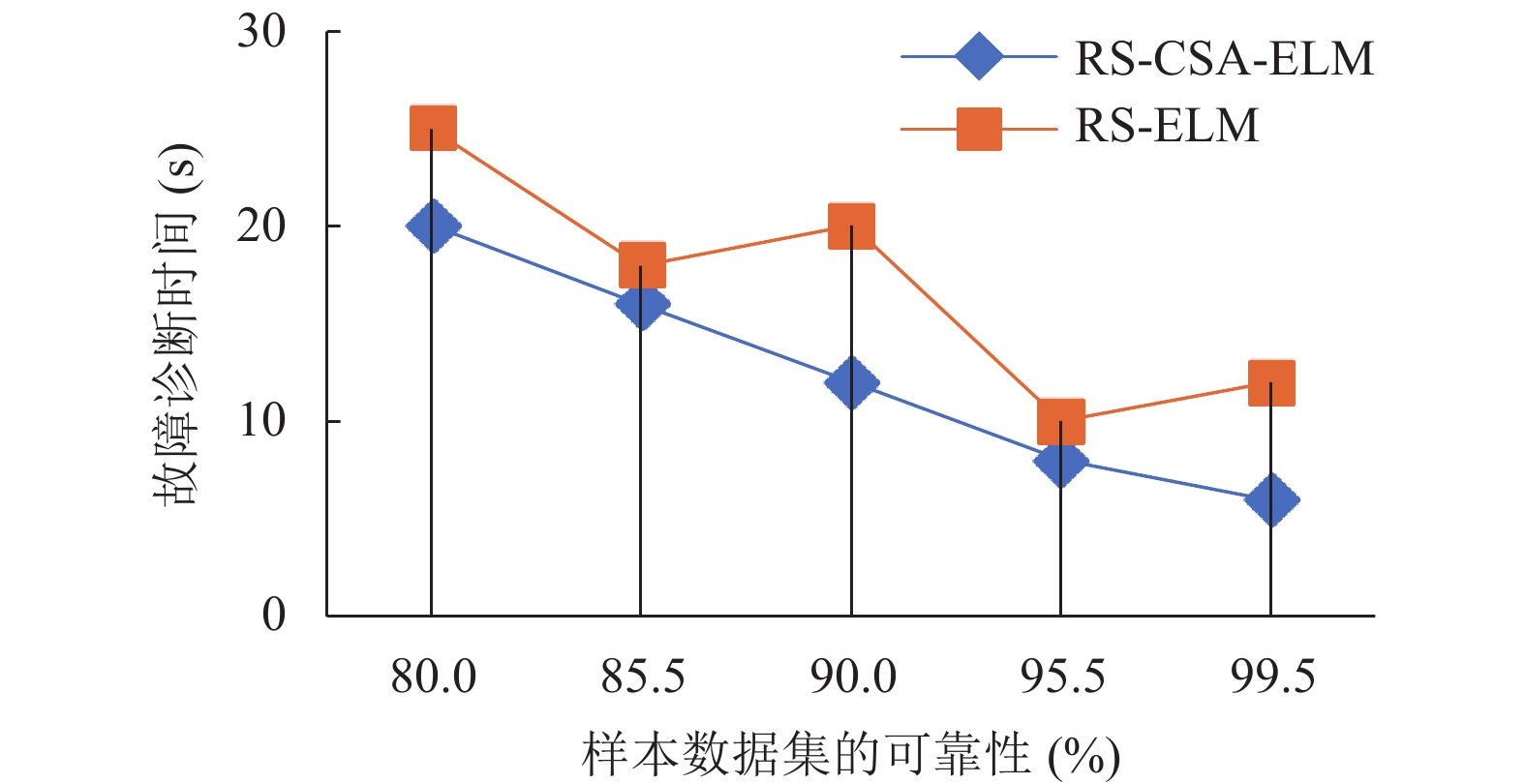
图 5 CSA优化前后的ELM故障诊断用时对比图 |
|
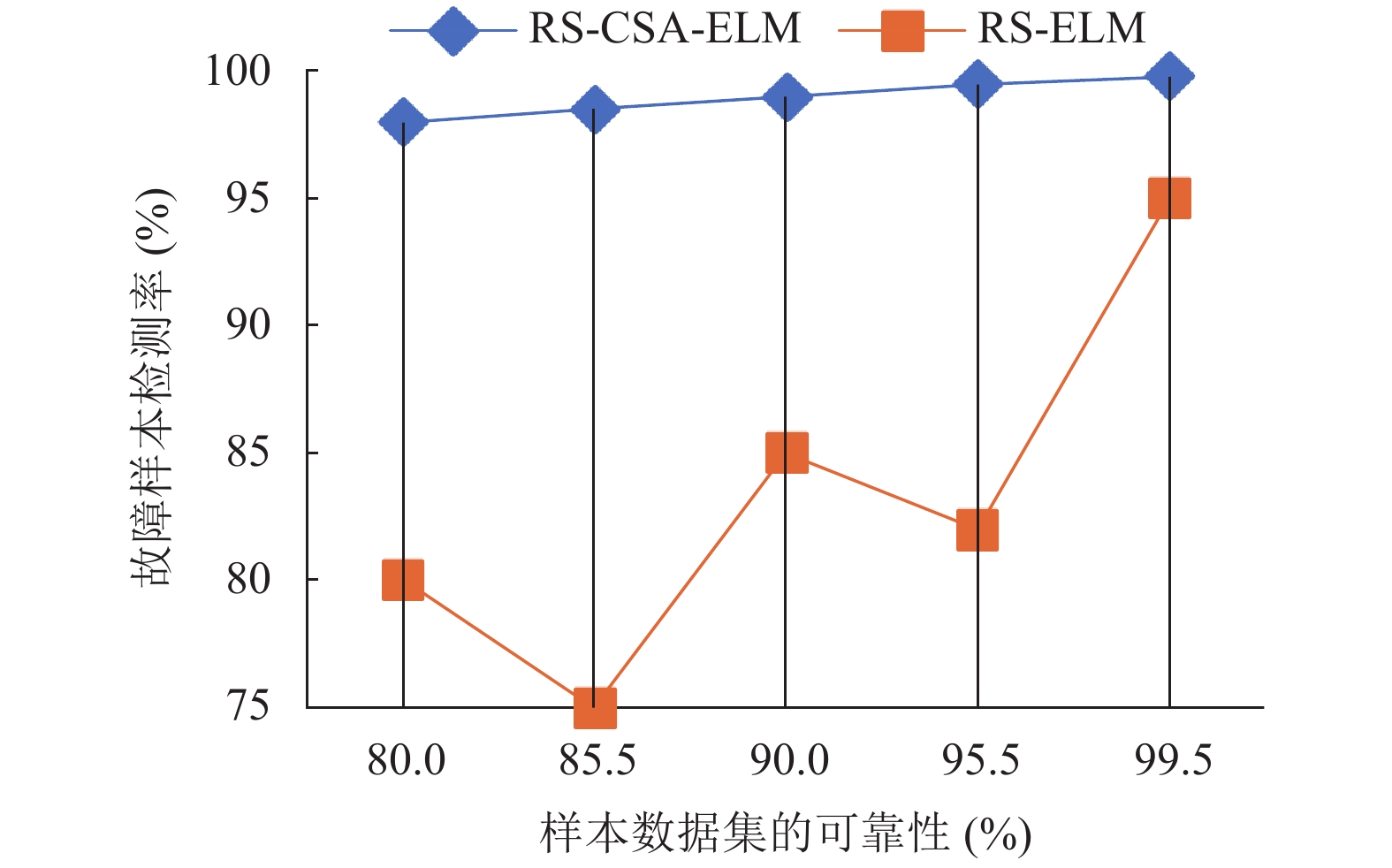
图 6 CSA优化前后的ELM故障检测精度比较图 |
其次, 对CSA优化RS-CSA-ELM模型的参数的做了仿真验证. 其结果如图7所示.
最后, 对可靠性为80%、85.5%、90%和99.5%样本数据集进行约简后, 将本文提的RS-CSA-ELM算法与文献[14]的RSOPNN算法及文献[15]的RS-PSO-KELM算法进行比较测试. 其结果如图8及图9所示.
从图5、图6可以看出经过CSA优化之后的ELM其稳定性得到了很大的提高; 从图7可以看出CSA在迭代到15次的时即可寻找到最优得ELM输入权值和隐含层阀值; 从图8可以看出3种算法对WSN节点故障诊断用时都是随样本数据集可靠性增加而减少, 但本文所提的RS-CSA-ELM算法与其它两种算法在相同条件下用时是最短的; 从图9可看出3种算法的诊断准确性随样本数据集可靠性增加而提高, 但本文所提的RS-CSA-ELM算法与其它两种算法在相同条件下诊断的准确性是最高的. 综上所述, 本文所提算法能够快而准的对WSN节点故障进行诊断识别, 且稳定性和诊断的准确性可满足实际应用要求.

|
图 7 CSA对RS-CSA-ELM模型寻优迭代次数图 |

|
图 8 算法诊断用时比较图 |

|
图 9 算法性能比较图 |
4 结束语
鉴于现有WSN节点在故障诊断方法的缺陷[16], 提出RS-CSA-KELM算法予以解决, 通过粗糙集理论属性约简算法(简称RS)对故障属性约简、利用CSA算法对EML的参数进行优化, 建立数据驱动式的RS-CSA-ELM故障诊断模型. 该模型对WSN节点故障的诊断快而准, 并能有效的解决误诊和漏诊等问题, 特别适合用于拓扑结构实时变化的网络的故障诊断. 当然, 所提之法仍需研究、改进, 如进一步考虑算法中各参数设置及各算法之间的优缺互补等问题.
| [1] |
丁晗. 无线传感器网络的故障节点侦测算法设计与分析[硕士学位论文]. 苏州: 苏州大学, 2016.
|
| [2] |
张新华. 基于ICA独立成分和加权依赖贝叶斯的传感器节点故障诊断. 重庆师范大学学报(自然科学版), 2015, 32(2): 138-142. |
| [3] |
曾庆杰, 朱晓娟, 王先超. 基于节能的WSN分簇式故障诊断算法. 阜阳师范学院学报(自然科学版), 2019, 36(4): 54-60. |
| [4] |
刘建伟. WSN节点故障诊断方法研究及测试平台设计[硕士学位论文]. 长沙: 湖南大学, 2017.
|
| [5] |
Sun YM, Liu XJ, Chen XG, et al. Research and application of a fault self-diagnosis method for roots flowmeter based on WSN node. Wireless Personal Communications, 2017, 95(3): 2315-2330. DOI:10.1007/s11277-017-4104-8 |
| [6] |
Duh DR, Li SP, Cheng VW. Distributed fault-tolerant event region detection of wireless sensor networks. International Journal of Distributed Sensor Networks, 2013, 9(9): 286-291. |
| [7] |
Oh SH, Hong CO, Choi YH. A malicious and malfunctioning node detection scheme for wireless sensor networks. Wireless Sensor Network, 2012, 4(3): 84-90. DOI:10.4236/wsn.2012.43012 |
| [8] |
周奚, 薛善良. 基于改进的粗糙集和神经网络的WSN故障诊断. 计算机科学, 2016, 43(S2): 21-25. |
| [9] |
郑茂辉, 刘少非. GA优化ELM神经网络的排水管道缺陷诊断. 哈尔滨工业大学学报: 1–7. http://kns.cnki.net/kcms/detail/23.1235.T.20200420.1814.002.html, [2020-04-29].
|
| [10] |
蒋鹏. 一种改进的DFD无线传感器网络节点故障诊断算法研究. 传感技术学报, 2008, 21(8): 1417-1421. DOI:10.3969/j.issn.1004-1699.2008.08.026 |
| [11] |
林涛, 郝章肖, 冯竞凯. 基于改进乌鸦搜索算法的云计算任务调度研究. 微电子学与计算机, 2020, 37(2): 20-24. |
| [12] |
王丽婷, 张金鑫, 张金华. 乌鸦搜索算法在SVM参数优化中的应用. 计算机工程与应用, 2019, 55(21): 214-219. DOI:10.3778/j.issn.1002-8331.1903-0381 |
| [13] |
Sun QY, Sun YM, Liu XJ, et al. Study on fault diagnosis algorithm in WSN nodes based on RPCA model and SVDD for multi-class classification. Cluster Computing, 2019, 22(3): 6043-6057. |
| [14] |
李洋, 高岭, 孙骞, 等. 基于RSOPNN的无线传感器网络节点故障诊断算法. 计算机工程与应用, 2017, 53(9): 111-116, 157. DOI:10.3778/j.issn.1002-8331.1511-0185 |
| [15] |
柴继超. 无线传感器网络节点故障诊断方法研究[硕士学位论文]. 哈尔滨: 哈尔滨理工大学, 2019.
|
| [16] |
Xing XD. Research on fault diagnosis technology of wireless sensor network based on improved frog leaping algorithm. Machine Tool & Hydraulics, 2019, 47(12): 97-102. DOI:10.3969/j.issn.1001-3881.2019.12.015 |
 2021, Vol. 30
2021, Vol. 30



