2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
针对CFD流场模拟结果的可视化处理是流体动力学分析的重要一环. 常用的流场可视化处理方法包括流线、轨迹线、FTLE分析等方法. 而上述方法的核心算法均为粒子追踪算法, 因此, 考虑到粒子追踪算法之于流场可视化的重要性, 为了提高流场可视化分析效率, 领域研究人员针对该算法的优化和并行化开展了一系列研究工作. 现有的并行化算法往往考虑的是比较单一的计算架构, 有的是基于共享存储的计算环境, 有的是HPC集群计算环境, 有的是结合GPU加速器的异构计算环境. 为了兼容各类型计算架构, 充分发挥异构并行计算环境的计算资源以实现流线快速生成, 我们基于自主研发的GPVis平台[1], 采用了数据并行原语结合分布式消息通讯的技术架构, 设计了一套流线生成系统, 通过数据并行原语实现设备无关的并行粒子追踪算法, 并结合数据空间域分解技术实现整个流场区域的流场生成任务的分而治之策略. 本文基于这一系列方法在国产超算平台上完成了该系统的实现和部署, 并与已有的流线生成系统在不同参数条件下进行了测试比较. 在对测试结果进行分析后, 我们发现新系统可有效改善传统流线生成方法的负载不均衡问题, 以较高的并行效率实现分布式计算环境下的可扩展计算.
1 研究背景 1.1 并行粒子追踪粒子追踪计算是流场可视化的重要算法之一. 而针对粒子追踪算法并行化的基本方法主要可分为两类: 种子点并行法Parallelize-Over-Seeds (POS)以及数据块并行法Parallelize-Over-Data (POD)[2]. 其中, POS算法的基本思想是将初始种子点均匀分布在各处理单元上, 并且让各处理单元进行独立计算. 而POD算法则是通过域分解将整体数据分为众多数据块, 并将各数据块分配到各处理单元, 然后每个处理单元负责完成进入该数据块的粒子的追踪计算, 直至粒子达到终止条件或进入其它数据块空间.
POS方法往往需要较大的计算设备内部存储空间来支撑, 或者需要通过频繁的I/O加载操作来消减一部分的内部存储空间需求. 这是由于POS方法并未针对数据分块方面制定域分解策略, 它要求每个节点在执行期间可以随机访问全部数据. 这就造成各处理单元要么在启动时读入所有数据, 要么将整个数据按空间分成小块再按需读取. 两种方法中前者的性能容易受到设备存储空间(系统内存以及GPU显存)的瓶颈限制, 后者则会带来较高的I/O相关的成本(如大量的I/O启动延迟所带来的时间成本, 或者为防止各计算单元的I/O操作之间的冲突而提供的高带宽并行I/O能力支撑而带来的硬件成本).
POD方法适用于高度可扩展的HPC环境, 可通过数据分块将单节点的内部存储空间需求降低到可接受的水平, 但同时由于任务的不可迁移也往往导致严重的负载不均衡问题.
鉴于两类基本方法存在的弊端, 研究人员在两类方法基础上, 发展出任务窃取法[3]、任务请求法[4]等混合并行方法. 混合并行方法一般会动态地且冗余地将数据块分配给各处理单元, 以实现更优的负载均衡, 同时也通过先验的规划或实时的策略来降低冗余数据读取所带来的附加的I/O操作对算法整体可扩展性的影响.
1.2 数据并行原语数据并行原语(Data Parallel Primitives, DPP)的设计思想最早来源于一种用于数据并行计算的扫描矢量模型[5]. 在数据结构、计算几何、图分析以及数值分析等众多算法领域, 扫描矢量模型被应用于重新设计各种算法以实现算法的并行化. 而数据并行原语DPP作为扫描矢量模型的升级版本, 可采用包括Map、Scan、Sort和Reduce在内的一些基础操作来实现各类并行算法. 从目前的研究来看, 除了Delaunay、FFT等少量算法, 在DPP模型基础上, 大部分的可视化算法都可以有相应的实现方法[6]. 虽然并不是所有可视化算法都可以通过DPP来实现, 但并不妨碍DPP模型在海量线程计算设备中的应用.
VTK-m[7]是较典型的且功能相对全面的一套基于DPP的可视化算法库. 为了发展适用于GPU、MIC等海量线程计算环境下的可视化算法, Kenneth等综合借鉴了PISTON[8]、Dax[9]和EAVL[10]等关注于海量线程计算的并行可视化架构的设计思想, 并在设备及算法通用性方面进行了优化, 于2016年提出了VTK-m并行可视化计算架构. VTK-m采用数据并行原语DPP作为算法并行化基本单元, 提供了一套与DPP兼容的计算设备抽象模型, 并针对底层硬件体系架构进行了兼容适配, 以提高VTK-m的兼容性和可移植性. 由于用户无需考虑底层硬件实现细节就可以设计实现各类高效率的算法, 因此VTK-m有助于降低海量线程计算环境下的并行算法的实现难度. 目前, VTK-m的计算设备抽象模型可兼容包括GPU、MIC在内的多种海量线程计算设备.
VTK-m将各类通用算法以基本任务单元的形式进行继承封装, 而基本任务单元的运行调度是通过各类符合DPP模型的设备适配器来驱动的(如图1所示). 这样, 基于VTK-m设计的可视化应用则可以通过底层设备适配器的切换而运行于各类海量线程环境. 通过VTK-m来编写可视化算法除了可保障算法的设备通用性之外, 在稳定性和安全性的保障方面也很便利. 例如, 如果通过Map映射操作来跟踪数据的拓扑连接时, VTK-m会在计算设备端的内部自动完成拓扑结构索引的处理而避免了不安全的操作, 这就使得编写基本任务单元比直接并行操作整体数据结构要更容易且更安全.

|
图 1 VTK-m可视化应用运行机制 |
1.3 基本任务单元
基本任务单元是指组成大规模数据并行处理程序的针对小规模数据的无状态的细粒度串行程序片段[11], 而采用DPP设计并行算法的核心任务之一就是基本任务单元的定义. 我们采用VTK-m来设计海量线程加速器环境下的并行粒子追踪算法. 由于VTK-m是面向共享内存的海量线程运行环境而设计的可视化算法库, 没有分布式存储及高成本通讯等问题, 而且计算资源受到单机能力顶值的限制, 不需要过多考虑算法的大规模扩展问题, 因此, 较适合采用POS的并行策略来设计并行粒子追踪算法. 但在实际算法设计中, VTK-m与传统的POS方法也有一定的区别. 比如在定义基本任务单元的层面, VTK-m虽然采用了与传统POS方法类似的做法, 将并行粒子追踪的基本任务单元定义为单个粒子的追踪任务, 但在细节上仍然与传统方法有所不同.
很多并行粒子追踪算法的基本计算单元将固定步数的单个或一组粒子追踪作为任务单元, 如文献[12]中采用的办法, 这样可以将计算粒度做到足够小, 从而有利于整体的负载均衡的实现. 但由于过小的粒度在异构计算环境下容易产生额外的调度开销, 因此, VTK-m并没有按这个方法来定义任务单元, 而是采用单个粒子的整条的追踪计算任务看作基本任务单元. 这样做既有利于降低任务调度开销, 也有利于降低任务单元之间的依赖性, 从而使得采用Map操作原语进行算法映射更为高效.
在确定了基本任务单元后, 只要将基本任务单元映射到一组执行线程上, 就可以通过海量线程计算设备的大规模并行能力来完成总体计算任务. 相应的, 在VTK-m的并行粒子追踪模块中, 采用设备无关的通用方式来描述单个粒子追踪基本操作的流程, 形成Advect函子, 然后通过Map操作来实现以函子形式封装的基本任务单元向底层并行计算设备的映射. Map操作是VTK-m中被高度优化的DPP之一, 针对底层硬件的特点采用了定制的任务映射方法以执行海量的基础任务单元. 特别是当运行环境是GPU这类加速器设备时, Advect函子所涉及的输入输出数据都将自动传输到设备内存中, 或者从设备内存中导出. 通过这种方式, 基本任务单元的执行位置实际上对开发人员是不可见的, 这也是为什么在编写基本任务单元时只能通过数组句柄来访问输入输出数据的主要原因.
2 系统设计受到单机计算存储能力顶值的限制, 大规模流场数据无法直接加载到单台机器的主线内存或加速器设备内存中. 因此, 无法仅靠基于GPU、MIC等海量线程计算硬件的并行粒子追踪系统来满足大规模流场数据可视化需求. 为了实现大规模流场的并行可视化, 我们需要在其基础上构建适用于异构集群环境的并行粒子追踪系统.
流场可视化方法常用于处理由CFD数值模拟产生的结果数据或中间数据. 而CFD模拟往往会因为计算过程的特点在各类不同的计算环境下运行, 因此, 流场可视化软件也需要适应如GPU加速器、SMP计算机、HPC计算机集群等各类不同的计算环境. 基于VTK-m的并行粒子追踪算法可以通过其架构中的计算设备适配器产生可运行于不同的计算硬件上的可执行程序, 具有很强的可移植性. 这是适应于上述的科学可视化运行环境特点的设计, 但美中不足的是, VTK-m并没有解决在大规模高性能计算机环境下开展可视化计算的问题, 这是因为在类似于SMP、GPU和MIC这种采用共享存储结合高速总线的体系架构中, 数据访问速度非常高, 无需过多考虑由于数据迁移所产生的时间消耗. 而HPC环境下却需要重点考虑如I/O、通讯等方面的负载对计算效率的影响. 这也正是本文中系统设计方面工作所面临的主要问题.
由于VTK-m可以在普通计算节点以及大规模线程环境下以粒子为处理单元并行地运行流线生成算法, 因此, 为了实现异构集群计算环境下的大规模并行粒子追踪, 我们只需要基于MPI消息通讯接口, 实现相关算法在HPC条件下的动态扩展即可. 为了达到上述目标, 我们设计了的适用于流场可视化的数据处理系统框架. 如图2所示, 系统框架结构包含5大部分, 分别为: 函子计算层, 数据分块层, 任务调度层, 进程通讯层以及渲染融合层.

|
图 2 并行粒子追踪系统结构图 |
(1) 函子计算层. 函子计算层负责调度单节点中的多线程或大规模线程资源, 以实现分配到单个节点上的可视化任务可以得到节点上足够全面的计算能力支撑. 在本系统中, 函子计算层的主要任务是基于VTK-m的多线程环境并行处理分配到节点本地的粒子追踪基本任务单元, 因此, 函子计算层主要是由VTK-m库以及之上的算法适配库组成. 通过继承和调用按VTK-m设计思想封装的基本任务单元模块WorkletMapField, 系统实现了兼容GPU、MIC等海量线程计算设备的并行粒子追踪模块.
(2) 进程通讯层. 进程通讯层主要负责节点进程间的基于MPI的消息接收和发送, 以及通讯相关的一系列并行算法, 主要模块包括消息通讯模块、数据交换模块以及进程协调模块. 其中消息通讯模块是对MPI接口的封装, 可用于体量小且实时性要求较高的消息的发送和接收. 数据交换模块在MPI协议基础上将节点间交换的大块数据封装成MPI数据包, 并逐包跟踪发送及接收进度, 以保证数据的顺序性和完整性. 进程协调模块包含了一系列分布式并行算法的MPI实现, 如扫描、搜索、合并、排序等. 在并行流线生成系统中, 粒子位置信息的交换以及积分结果曲线的汇总过程中需要用到较多的通讯资源, 此时需调用进程通讯层相关模块完成相应任务.
(3) 任务分布层. 任务分布层主要负责各节点及进程中计算任务的全生命周期管理. 从初期的任务创建, 到中期的任务执行以及任务迁移, 再到最后的任务回收, 任务分布层各功能模块以任务为单元跟踪其即时状态, 并根据任务的起始条件、终止或暂停条件调整任务的执行状态, 根据任务的数据需求以及节点的负载情况, 按总体任务调度策略发送或接收任务, 完成任务负载在节点间的流动. 由于任务执行过程采用的是基于VTK-m的多线程架构, 因此任务分布层还需要在线程级实现基本任务单元的调度运行, 从而实现线程级和进程级任务的有机融合.
(4) 数据分块层. 数据分块层主要负责实现可视化算法并行化中的域分解策略(如循环分块、八叉树分块、二分树分块等), 并在数据分布、存储及I/O等方面提供可调用的接口. 其中数据分布策略在并行算法中的I/O消耗最小化、负载均衡化等方面起到非常关键的作用, 尤其是对于粒子追踪这类负载不可预测的情况. 数据分布过程中单元数据块大小、重叠区域的设置、数据区块的节点分配都对可视化算法的整体运行效率以及负载均衡有很大影响. 在本文中, 我们针对并行粒子追踪算法中区域划分策略及冗余扩充策略进行了讨论, 并设计了新算法, 具体方法请见第3节.
(5) 渲染融合层. 渲染融合层主要负责图像相关的计算任务生成、执行以及合并操作, 主要功能包括图像渲染、图层融合、图元拼合等功能. 该层算法主要针对于图像并行的并行可视化算法, 而该类算法在体绘制和光线追踪法渲染等可视化应用中更为常见. 在本文所涉及的任务范围中, 渲染融合层只负责流线在并行生成并汇总后的单机渲染.
3 算法实现及改进正如1.1节中分析的那样, 包括POS和POD在内的基础并行算法均存在较严重的弊端, 而现有的混合并行算法有些并不适用于异构集群环境, 有些则存在各种其它问题, 如基础任务单元不兼容、包含整体预先分析处理步骤等.
为了避免上述问题, 我们设计了一套混合并行粒子追踪算法, 在总体的并行策略上采用了POD并行策略, 而在每个节点上由于采用了多线程的共享存储架构, 因此在节点层面上为了充分利用本地的存储计算资源采用了基于VTK-m实现的POS并行粒子追踪策略.
以下针对本文提出的混合并行算法中的具体方法进行说明如下.
3.1 粒子追踪算法设f为流场, y0为预设种子点, 则由该流场生成的流线是指如下常微分方程的解:
| $\begin{array}{*{20}{c}} {\dfrac{{{\rm{d}}y(s)}}{{{\rm{d}}s}} = y'(s) = f(y(s));}&{y({s_0}) = {y_0}} \end{array}$ |
其中, y(s)是一个关于沿流线方向的参数化步长距离s的三维位置函数. 求解流线的过程一般采用沿流线方向逐步积分的办法, 这个过程我们称之为粒子追踪过程. 粒子追踪过程其实质是粒子在流场作用下不断进行积分推进的过程, 常用的粒子追踪算法包括2阶、3阶、4阶以及4.5阶的龙格库塔积分方法. 本系统采用的是4阶龙格库塔积分求解方法.
采用DPP+POD策略的并行粒子追踪算法让不同的进程分管不同的数据块区域, 其算法如算法1所示. 因为积分过程会将粒子推向一系列难以预测的空间位置而形成流线, 而组成流线的这些空间位置有可能属于分布于不同进程的不同的数据块区域, 所以各个处理进程在计算本地的粒子积分的同时, 还需要接收可以落入本地数据区域的粒子, 以及将由于积分推进跨界进入非本地所属数据区域的粒子准确发送到数据块所属进程. 由上述流程可看出, 各进程无法仅根据自身情况判断计算过程是否可以终止, 而是需要将一个全局的统计信息作为终止条件来进行判断, 这就为算法的大规模并行带来了难度, 是实现算法高可扩展性所必须解决的问题. 另外, 与传统的POD策略并行算法不同的是, 由于基本任务单元的差别, 积分计算前将按份抽取一定量的粒子进行积分, 每份粒子的数量要求与海量线程计算设备的线程个数尽量接近.
算法1. 基于DPP+POD策略的并行粒子追踪算法
1) 加载本进程负责的数据块和种子点粒子, 已终止粒子累积计数器置零;
2) 判断本地粒子数是否为0, 如为0则到步骤9);
3) 从全部本地粒子中取出一份粒子;
4) 调用Map操作原语在多线程设备中对取出的粒子执行粒子追踪, 得到一部分已终止粒子和另一部分跨界粒子;
5) 将本轮已终止粒子数广播到全部进程;
6) 将本轮已终止粒子数累计入已终止粒子累积计数器;
7) 接收由其它进程广播发出的已终止粒子数, 并全部累计入已终止粒子累积计数器;
8) 对跨界粒子排序, 按粒子当前位置所属进程号将全部跨界粒子发送至所属进程;
9) 接收由其它进程发出的跨界粒子, 存入本地粒子库;
10) 判断当前已终止粒子累积计数器值是否与粒子总数相等, 如相等则退出, 否则转到步骤2).
3.2 数据分块实际上, 由于流场本身的不确定性, 粒子追踪的负荷在空间域的分布是随机的, 因此, 在没有先验信息的前提下, 采用数据无关的分块策略肯定是无法达到最佳的负载均衡的. 这也正是循环分块法建议在每个节点增加数据块数, 以逼近更均衡的负载分布的原因.
粒子追踪中较常用的数据分块策略包括循环分块法[13]、k-D树分块法[14]等. 循环分块法注重于计算进程的负载均衡, 因此该算法在每个进程分配散布于空间不同位置的数据块, 以缓解由粒子聚集所导致的负载失衡. 为实现进程中各个数据块的空间均匀散布, 循环分块法会要求进程个数不能被任意维度的网格数整除. 但是, 循环分块法选择忽略由于粒子流动本身的空间连续性而造成的算法邻域空间强相关性, 从而导致较高的节点间通讯量并极大地影响了整体并行效率. 而k-D树分块法想尽量避免粒子的跨节点漂移以减少节点间通讯从而提高并行效率, 该方法针对粒子分布来进行数据块的分配, 适用于面向时变流场可视化的动态分块策略, 但这种策略不适用于将粒子整条追踪过程设置为基本任务单元的算法, 因为该方法要求在追踪过程中检查粒子位置. 另外, 循环分块法采用固定的块大小也不利于算法的灵活性和可扩展性.
为了改善循环分块法的以上问题, 我们采用了递归二分法进行空间分块. 假设采用N个计算进程开展并行计算, 每个进程要求分配nb个数据块, 那么, 首先对整个数据空间进行多次切分, 切分原则为在3个维度中选择最长轴进行切分, 在多次切分后, 分块数总能超过N×nb块, 再将部分多余的分块与相邻分块融合后, 分块数可达到N×nb块, 从而满足数据分布化需求. 同时, 为减少维度分块数与进程数之间可能存在的整除关系所带来的数据块空间聚集的可能性, 各数据块将在随机洗牌后再进行循环分配.
3.3 数据冗余化并行算法的可扩展性与执行过程中的通讯量以及负载均衡程度紧密相关. 针对并行粒子追踪算法, 数据通讯主要发生在粒子跨越数据块边界进入另一个数据块的情况, 因此, 当粒子所属数据块足够大时, 越界情况发生的机率将会减少. 另外, 并行粒子追踪过程中负载失衡的主要原因在于某些区域存在相对低速区域、涡旋、临界点等需要长时间积分才能通过甚至无法通过的区域(又称为陷阱区), 尽管可以采用如文献[13]中所述办法, 在经过判断后发现这类粒子时立刻中止该粒子积分过程, 但这种办法实际阻断了后续结果的计算, 有可能对流场分析过程产生干扰, 而且基于VTK-m的任务单元定义方法也决定了不可能在计算中途阻断粒子积分, 而这种情况也为整体系统的并行效率提升增加了难度.
由前面的分析可看出, 不管是在降低数据通讯量或是提升负载均衡程度的解决办法中, 在无重叠的数据分块的基础上, 将数据区域进行冗余化扩充都是有效的办法之一, 我们称之为数据冗余化. 在并行算法中, 区域重叠法通过建立重叠区来扩展数据区域是最常用的数据冗余化策略. 重叠区又称为鬼区, 在多类并行算法中均有采用, 当然也包括一些并行粒子追踪算法.
3.4 进程间通讯并行粒子追踪算法中主要的进程间通讯分为两类: 一类是由于粒子越界所造成的负载流动, 这类通讯是点对点的通讯, 但具有随机不可控的特性, 无法预测通讯发生的位置和数量; 另一类是粒子终止状态汇报所产生的进程间通讯, 这类通讯是点对全体的通讯, 需要将单个进程的计算结果汇报到所有进程, 让每个进程了解当前已完成积分的粒子数, 在全部粒子完成积分时终止等待负载的工作循环, 进入流线生成的收尾阶段.
粒子在流场推动下会在不同的数据块区域之间移动, 由于不同的数据块预先指定由不同的进程负责, 因此积分计算负载将不可控地且被动地在进程间流动, 从而造成可能的负载聚集. 通过前面讲到的循环数据分块方法, 我们可以缓解这种负载聚集带来的通讯量聚集. 另外, 由于频繁的发送越界粒子有可能造成通讯数量过, 多且接收粒子的进程有可能在收到不足份的粒子前就开始积分计算从而造成计算时间的浪费, 因此, 改进的算法会在一个时间段里累积一部分越界粒子, 当粒子数量达到足份量时才进行发送, 除非在该时间段里无法累积到足量的粒子, 此时只能将全部越界粒子发出.
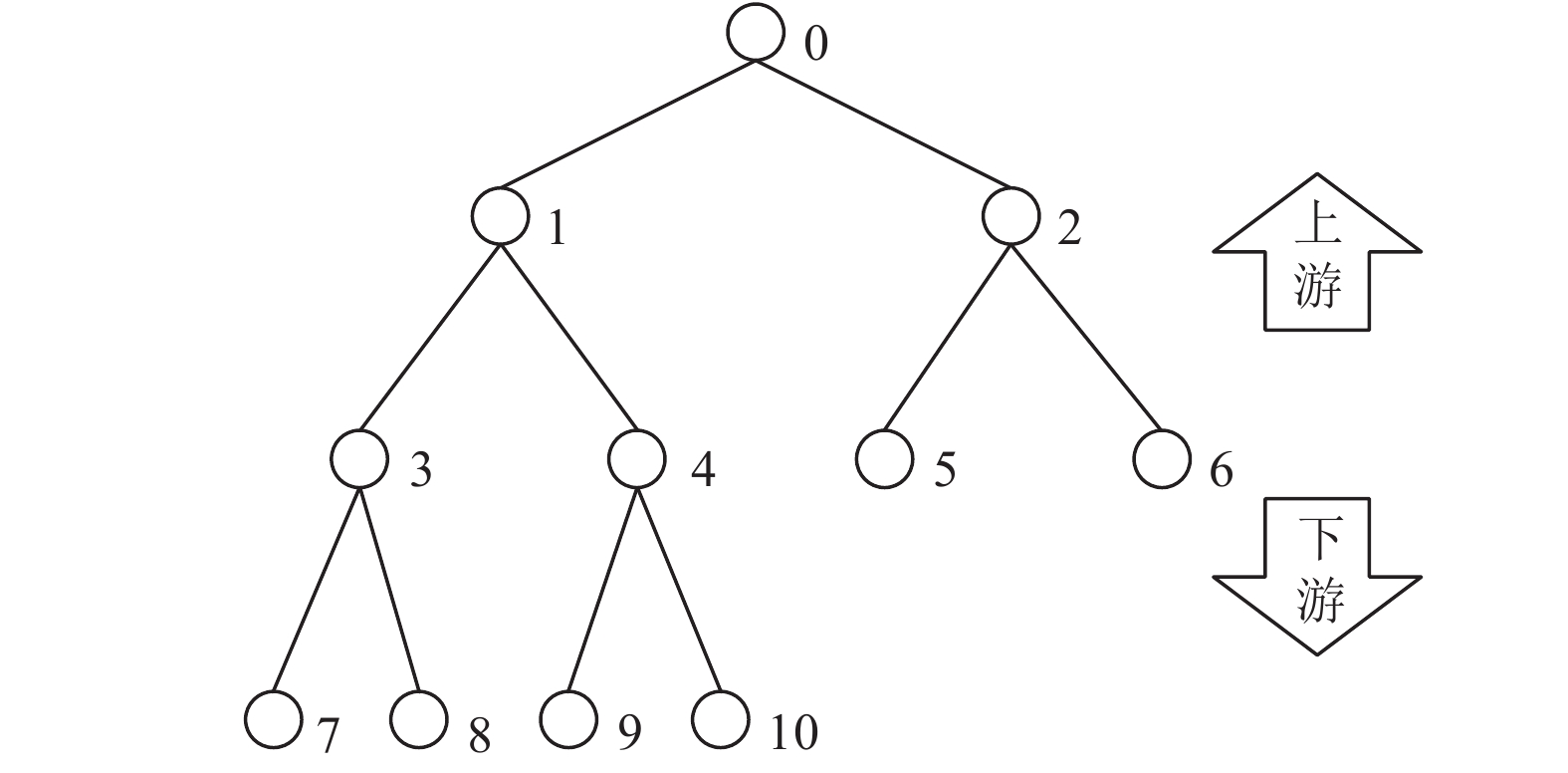
对于粒子终止状态汇报机制, 原有的广播形式的汇报算法实际上是非常昂贵的, 尤其是在进程数足够大时, 广播通讯的规模以几何规模增长, 对整体的扩展性能产生了非常大的影响. 为了改善这一情况, 我们设计了一套树型汇报机制, 如图3所示.
|
图 3 树型状态汇报机制示意图 |
如图3中, 所有进程被组织成二叉树的节点, 每个进程最多有一个上游进程和两个下游进程, 当下游进程汇报粒子终止情况下, 上游进程进行统计汇总再上报上游进程, 当最上游根进程发现全部粒子积分均终止时, 将向下游进程发送退出循环的信号并退出循环, 其它进程在收到退出循环信号后也进行同样操作. 整个通讯进程是异步且点对点的, 因此对整个计算过程的影响被降到最小. 经改进的并行算法如算法2所示.
算法2. 改进的基于DPP+POD策略的并行粒子追踪算法
1) 加载本进程负责的数据块和种子点粒子, 已终止粒子累积计数器置零, 打开循环开关;
2) 判断本地粒子数是否为零, 如为零则转到步骤12);
3) 从全部本地粒子中取出一份粒子;
4) 调用Map操作原语在多线程设备中对取出的粒子执行粒子追踪, 得到一部分已终止粒子和另一部分跨界粒子;
5) 对跨界粒子排序, 按粒子当前位置所属进程号将全部跨界粒子发送至所属进程;
6) 接收下游进程发来的经汇总的已终止粒子数消息, 并与本轮已终止粒子数相加得到待发送的经汇总的已终止粒子数;
7) 向上游进程发送经汇总的已终止粒子数;
8) 将经汇总的已终止粒子数累计入已终止粒子累积计数器;
9) 判断当前已终止粒子累积计数器值是否与粒子总数相等, 如相等则转到步骤11), 否则转到步骤12);
10) 接收上游发送的退出循环指令, 如未收到则转到步骤12);
11) 关闭循环开关, 并向下游进程发送退出循环指令;
12) 接收由其它进程发出的跨界粒子, 存入本地粒子库;
13) 判断循环开关是否打开, 如关闭则退出, 否则转到步骤2).
4 应用测试 4.1 测试环境我们在国产高性能计算集群上开展了系统和算法的相关测试. 该集群每个节点包含32个海光C86 7185 CPU (32核, 主频2.0 GHz), 128 GB内存. 编译器采用Intel编译器, 启用OpenMP与VTK-m相结合实现多线程并行, 多节点分布式并行MPI环境采用的是OpenMPI, 我们根据实验需要使用了1至256个节点开展测试.
4.2 测试数据及方法我们采用了由CFD模拟程序实际产生的数据来开展算法测试. 该测试数据是一套燃烧模拟结果数据[15,16], 其网格分辨率为670×459×459, 包含亿级网格规模. 相关的CFD模拟实验模拟了超音速喷射的可燃气体在空气中混合燃烧产生涡流的过程, 以研究燃烧反应过程对涡结构的影响. 模拟采用的是OpenCFD-Comb模拟程序. 本次测试只采用了一个时间步, 以实现基于可视化的稳态流场分析. 图4显示了该数据的流场可视化效果.
我们采用了16至1024个进程开展并行粒子追踪计算, 单个粒子的追踪步数最大值设定为10000步. 并行化方法均采用经过随机排序的递归二分法进行数据分块, 并采用了区域重叠最大化的数据冗余化策略, 单进程限定的内存使用规模为64 MB. 为了测试系统性能, 我们在相同的运行环境下编译运行了ALPINE系统[17]中的粒子追踪模块, 并基于相同的数据以及计算目标进行了对比测试. ALPINE系统中的粒子追踪模块是同样采用了VTK-m作为核心计算库的异构并行可视化软件.

|
图 4 测试数据可视化效果图 |
4.3 性能对比分析
我们设计了一套强扩展测试方案, 即通过总量固定的任务量来测试并行算法在不同的节点进程数的情况下的加速效率. 对于粒子追踪算法来说, 在设置固定的粒子总数的前提下, 将积分任务均匀分布到各节点或进程上开展强扩展测试, 我们可以测量并观察总的执行时间是如何随进程数的变化而发生变化的. 理想状态下, 加速比将线性增加. 而实际上对于进程间存在通讯的并行算法来说, 在进程数达到一定规模的情况下会出现加速比无法提升甚至下降的情况.
本次测试按两种粒子规模进行了粒子追踪测试, 其粒子规模n分别为1兆以及2兆. 测试结果如图5所示. 其中图5(a)为跟踪1兆粒子时的计算时长与核数关系图, 图5(b)为对应的负载均衡与核数关系图, 图5(c)为跟踪2兆粒子时的计算时长与核数关系图, 图5(d)为对应的负载均衡与核数关系图. 从测试结果可看出, ALPINE系统在核数达到512核之后迅速表现出背离加速方向的发展趋势, 且在数据规模相对较大时, 这种趋势更为明显且出现的时间也更早, 如图5(c)所示, 针对2兆粒子进行粒子追踪时, 核数达到128核之后, 该系统就无法进一步实现计算时间的缩减. 相比较而言, GPVis平台的粒子追踪系统在核数达到1024核的规模时, 仍然表现出加速潜力, 且整体加速趋势趋近于线性加速.
4.4 负载均衡分析图5(b)和图5(d)通过负载失衡度这一指标说明了计算过程的负载均衡情况. 负载失衡度是各进程中进程最大负载与各进程平均负载的比值. 从图可看出, 两组测试表现出相似的模式, 即ALPINE在核数达到256核之后, 负载失衡的情况迅速恶化, 而GPVis在核数增加时, 负载失衡度略有提升, 但仍在可控范围. 从两组测试结果中也可看出不同之处, 在数据规模相对较大时, ALPINE的失衡度升高较快, 而GPVis的负载失衡度受到数据规模的影响几乎可以忽略.

|
图 5 系统强扩展性能测试对比图 |
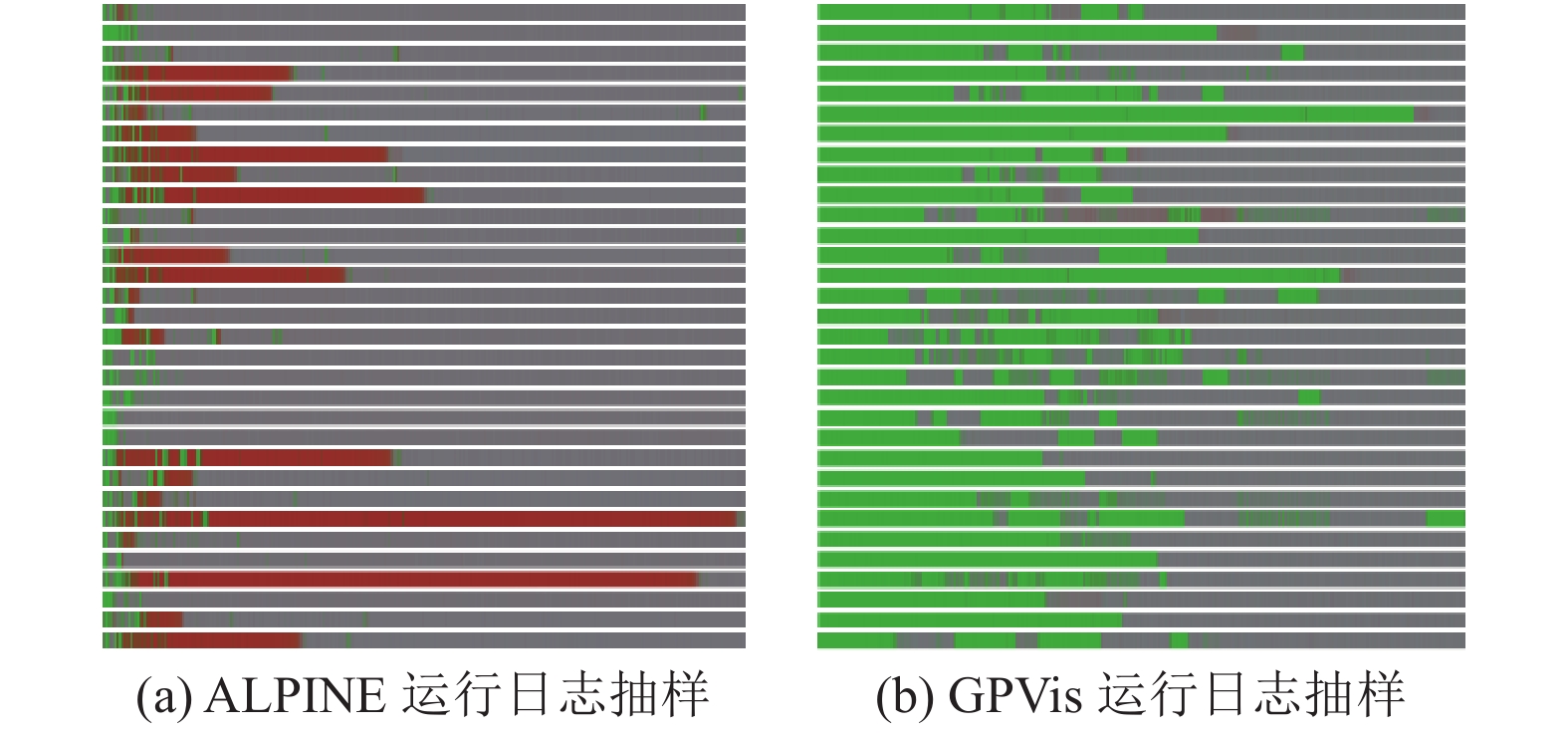
在对运行过程中的具体计算日志进行详细记录后, 我们发现了两者的主要区别. 我们记录两组测试中512核的运行日志, 并在512个进程中选取了32个进程进行可视化, 图6即为两组运行测试日志的可视化结果, 图6(a)为ALPINE运行日志的抽样, 图6(b)为GPVis运行日志的抽样. 图中每个横条代表一个进程的工作状态发展过程, 向右方向为时间方向, 两组横条的长度被归一化为相同的长度, 以表现整个计算过程. 横条中绿色代表计算时间, 红色代表通讯时间. 从图中可看出, ALPINE系统由于采用了全局广播通讯的终止粒子汇报机制, 当核数增加时, 相应的通讯时长逐渐占据主导而拖慢了整体性能, 而GPVis粒子追踪系统采用的优化的终止粒子汇报机制, 相应的通讯压力则非常小, 从整个计算周期来看, 占据非常小的比例. 这也是图5中两者负载失衡度变化趋势发生区别的主要原因.
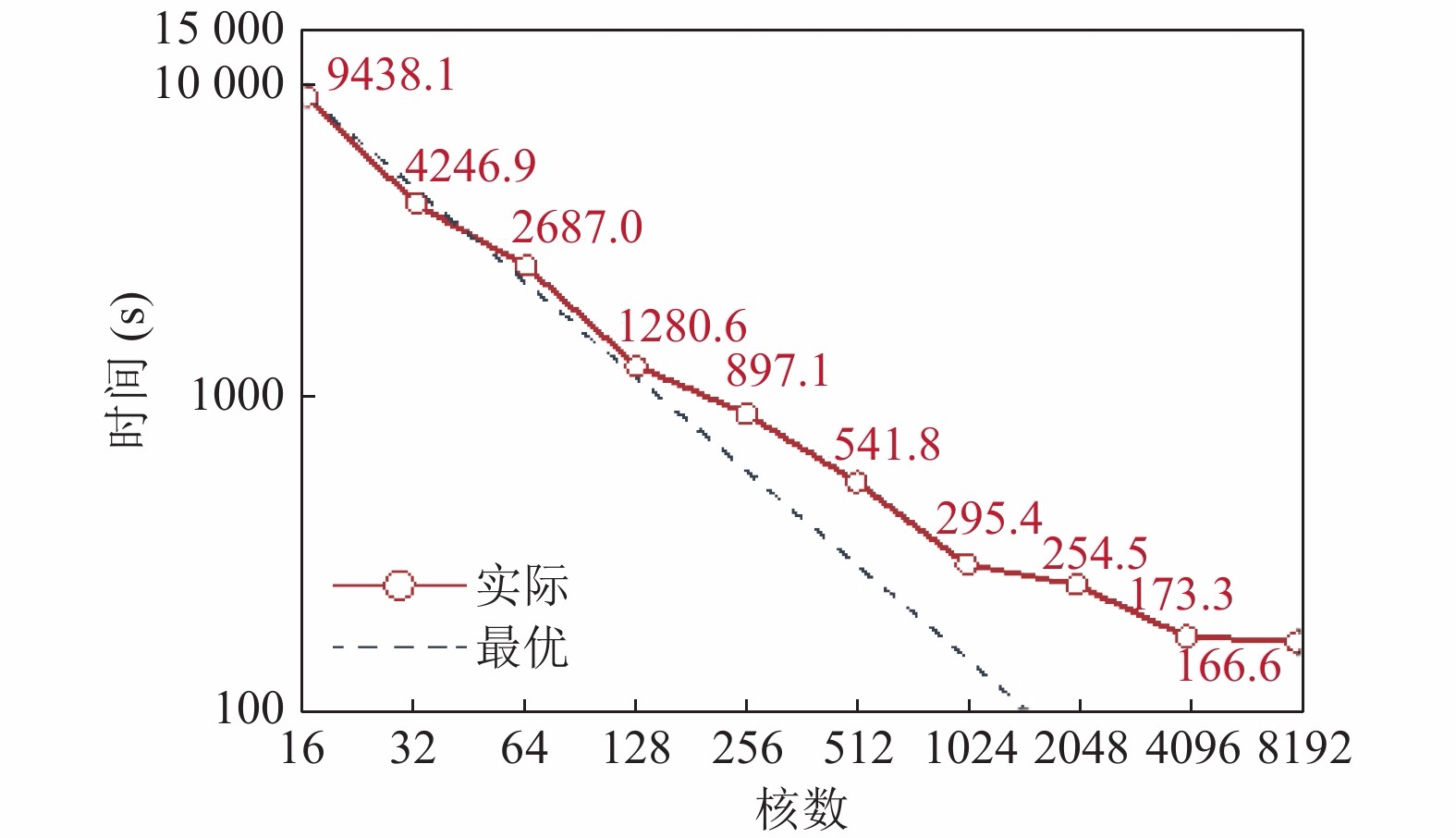
4.5 大规模测试分析当采用FTLE进行流场分析处理时, 需要开展大规模的流线生成计算, 计算规模为每个网格点设立一个被追踪的粒子. 那么对于本案例针对数据来说, 粒子数取与网格数相当的规模后大小约为140兆. 针对这一规模, 我们开展了相应的测试. 测试结果如图7所示, 从中可看出, 目标系统在较大的计算负载下且当核数达到万核级别时依然表现出可接受的加速趋势, 但并行效率则在1024核的50%之后出现快速下降, 其中在采用2048核、4096核和8192核时的并行效率分别为29%、21.3%和11.1%.
|
图 6 系统运行甘特图对比 |
|
图 7 大规模粒子追踪任务测试结果 |
4.6 测试小结
从测试结果可看出, 本文提出的系统及算法可适用于异构集群计算环境, 且在计算速度、可扩展性等方面表现优于ALPINE系统粒子追踪模块. 经过细致的运行日志分析, 我们发现了文中提出进程通讯算法优化方法在系统整体的可扩展性提升及负载均衡化方面起到了重要作用. 经过大规模测试分析, 我们认为, 本系统可用于大规模集群环境下的并行流线生成及流场分析场景.
5 结束语本文针对异构集群环境下的并行流线生成系统提出一种改进的基于POD+DPP的粒子追踪算法设计实现方案, 并针对流线生成过程中的粒子追踪算法的并行化的实现细节进行了分析和介绍. 在针对流线生成系统的并行测试后, 我们发现该系统可实现大规模CFD流场的流线并行生成, 达到了理想的可扩展能力, 并且在并行规模达到千核级别时仍表现出较高的并行效率, 在核数提高至万核级别时保持计算时长持续减少.
由于这次测试针对的数据属于稳态流场数据, 因此并未涉及非稳态流场的分析问题. 稳态流场与非稳态流场的流场或轨迹线生成方法有很大的差别, 前者更注重计算的分配, 后者更注重数据的动态加载过程, 后续我们将对本系统进行进一步升级, 并应用于时变流场的可视化处理. 另外, 从性能分析结果中可看出, 本文提出的优化方法虽然较传统方法提高了计算时间占用率, 但在进程数较多时并行效率仍然处于较低的水平, 存在进一步优化的空间.
| [1] |
单桂华, 刘俊, 李观, 等. 面向大规模数据的科学可视化系统GPVis. 数据与计算发展前沿, 2019, 1(1): 46-62. |
| [2] |
Pugmire D, Childs H, Garth C, et al. Scalable computation of streamlines on very large datasets. Proceedings of Conference on High Performance Computing Networking, Storage and Analysis. Portland, OH, USA. 2009. 1–12.
|
| [3] |
Dinan J, Larkins DB, Sadayappan P, et al. Scalable work stealing. Proceedings of Conference on High Performance Computing Networking, Storage and Analysis. Portland, OH, USA. 2009. 1–11.
|
| [4] |
Müller C, Camp D, Hentschel B, et al. Distributed parallel particle advection using work requesting. Proceedings of 2013 IEEE Symposium on Large-Scale Data Analysis and Visualization (LDAV). Atlanta, GA, USA. 2013. 1–6.
|
| [5] |
Blelloch E. Vector Models for Data-parallel Computing. Cambridge: MIT Press, 1990.
|
| [6] |
Moreland K, Geveci R, Ma KL, et al. A classification of scientific visualization algorithms for massive threading. Proceedings of the 8th International Workshop on Ultrascale Visualization. Denver, CO, USA. 2013. 1–10.
|
| [7] |
Moreland K, Sewell C, Usher W, et al. VTK-m: Accelerating the visualization toolkit for massively threaded architectures. IEEE Computer Graphics and Applications, 2016, 36(3): 48-58. DOI:10.1109/MCG.2016.48 |
| [8] |
Lo LT, Sewell C, Ahrens J. PISTON: A portable cross-platform framework for data-parallel visualization operators. The Eurographics Association. 2012. 11–20.
|
| [9] |
Moreland K, King B, Maynard R, et al. Flexible analysis software for emerging architectures. Proceedings of 2012 SC Companion: High Performance Computing, Networking Storage and Analysis. Salt Lake City, UT, USA. 2012. 821–826.
|
| [10] |
Meredith JS, Ahern S, Pugmire D, et al. EAVL: The extreme-scale analysis and visualization library. The Eurographics Association. 2012. 21–30.
|
| [11] |
Moreland K, Ayachit U, Geveci B, et al. Dax toolkit: A proposed framework for data analysis and visualization at extreme scale. Proceedings of 2011 IEEE Symposium on Large Data Analysis and Visualization. Providence, RI, USA. 2011. 97–104.
|
| [12] |
Sisneros R, Pugmire D. Tuned to terrible: A study of parallel particle advection state of the practice. Pugmire 2016 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW). Chicago, IL, USA. 2016. 1058–1067.
|
| [13] |
Peterka T, Ross R, Nouanesengsy B, et al. A study of parallel particle tracing for steady-state and time-varying flow fields. Proceedings of 2011 IEEE International Parallel & Distributed Processing Symposium. Anchorage, LA, USA. 2011. 580–591.
|
| [14] |
Zhang J, Guo HQ, Hong F, et al. Dynamic load balancing based on constrained K-D tree decomposition for parallel particle tracing. IEEE Transactions on Visualization and Computer Graphics, 2018, 24(1): 954-963. DOI:10.1109/TVCG.2017.2744059 |
| [15] |
Fu YW, Yu CP, Yan Z, et al. The effects of combustion on turbulent statistics in a supersonic turbulent Jet. Advances in Applied Mathematics and Mechanics, 2019, 11(3): 664-674. DOI:10.4208/aamm.2018.s10 |
| [16] |
Fu YW, Yu CP, Yan Z, et al. DNS analysis of the effects of combustion on turbulence in a supersonic H2/Air jet flow. Aerospace Science and Technology, 2019, 93: 105362. DOI:10.1016/j.ast.2019.105362 |
| [17] |
Larsen M, Ahrens J, Ayachit U, et al. The ALPINE in situ infrastructure: Ascending from the ashes of strawman. Proceedings of the in Situ Infrastructures on Enabling Extreme-Scale Analysis and Visualization. Denver, CO, USA. 2017. 42–46.
|
 2021, Vol. 30
2021, Vol. 30



