海洋石油平台达到报废年限后若没有其它用途就必须进行拆除. 根据HIS的研究报告未来五年将有600多座平台达到拆除条件, 海工平台拆除市场巨大^[1,2]. 桩腿内切割方式因具有作业效率高、风险低等优点被广泛应用于废弃导管架平台的拆除工作中; 桩腿切割前需在桩腿内进行抽泥作业, 使桩腿内泥面降至内切割工作位置. 清淤泵是桩腿内抽泥系统的核心设备之一, 对抽泥系统的性能起着决定性作用.

清淤泵的工作性能由多个指标所决定, 选择清淤泵时需对各指标进行综合分析. 计三有等^[3]将三角模糊数引入到模糊层次分析法中, 并利用其对大型集装箱码头堆放设备进行了综合评价, 有效减少了专家主观因素的影响; 王宇等^[4]利用模糊层次分析法对数控机床设备进行优化选择, 分析得出了数控机床设备的最优方案; 牛清娜等^[5]利用模糊层次分析法进行机械设备维修策略决策, 降低了设备维修的费用. 陈希祥等^[6]利用模糊层析分析法建立了测试设备的选择评判模型, 为测试设备选择提供合理依据.

清淤泵的配置选型是一个多准则、多属性的复杂决策过程. 为了实现清淤泵的科学配置选型, 本文基于熵权-模糊层次分析法建立了清淤泵的数学评价模型, 并通过计算分析得出了清淤泵的综合评价权重, 从多种性能相近的清淤泵型号中选出了最优方案.

1 清淤泵性能评价方法及评价体系 1.1 熵权-模糊层次分析法

模糊层次分析法是一种主观赋权法, 通过专家的赋分来确定各个指标权重的大小, 其权重的选择受专家主观经验影响较大^[7]; 而熵权法是根据系统的各指标提供的信息来确定权重的方法, 熵表征各指标的离散程度, 指标的离散程度越大, 则对综合评价的影响越大^[8]. 熵权-模糊层析分析法是在模糊层次分析法的基础上利用熵对准则层的指标权重进行了修正, 有效的减少了主观因素对评价结果的影响, 使得评价更符合实际情况.

1.2 清淤泵性能评价体系

桩腿内抽泥系统中清淤泵的性能直接决定了系统的效率、安全和可靠性等问题. 清淤泵的选择首先应满足抽泥系统的作业工艺要求, 即保证清淤泵的工作扬程、流量、功率达到最佳状态; 其次, 受桩腿内抽泥系统作业空间狭小的影响, 清淤泵的安装尺寸、出口直径、重量等指标也需要严格控制; 最后, 清淤泵的维修周期、使用寿命、供货周期等应尽可能满足海洋工作环境及任务安排的需求, 即在工作周期内能够保证较高的使用性能. 根据清淤泵的工况需求, 从桩内抽泥系统的作业工艺要求、工作环境、经济性等因素出发, 确定清淤泵性能的评价指标.

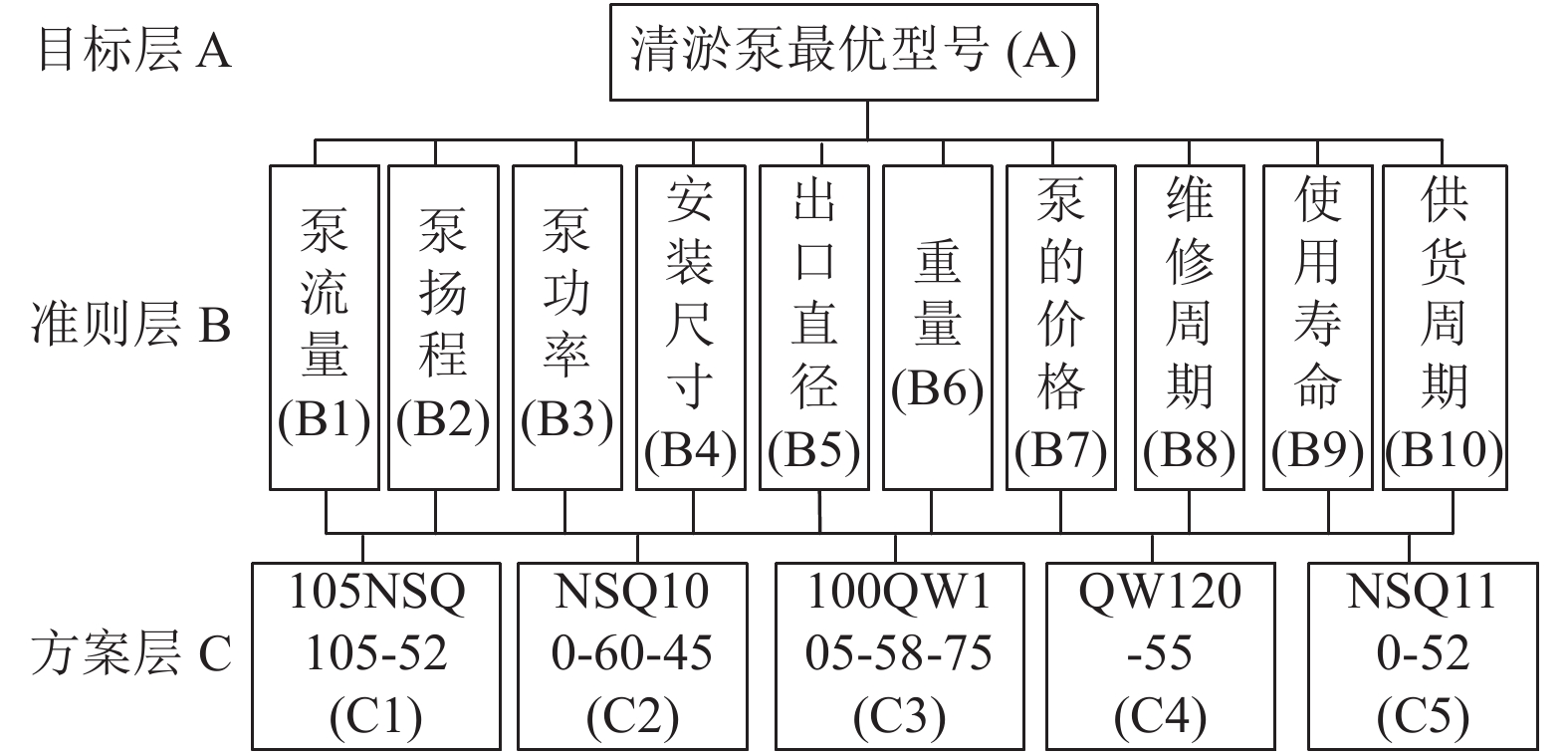
根据抽泥系统的工作特点, 综合考虑以上影响因素, 以清淤泵的最优型号为目标层, 以清淤泵性能评价的具体指标为准则层, 以清淤泵的配置方案为方案层, 建立清淤泵的性能评价递阶层次模型, 如图1所示.

2 熵权-模糊层次分析法数学理论模型 2.1 建立层次分析模型

某配置决策方案的方案集 $C = \{ {C_1},{C_2}, \cdots ,{C_n}\} $ , 评价指标集 $B = {\rm{\{ }}{B_1},{B_2}, \cdots ,{B_m}\} $ ,指标参数矩阵 $X = {\left( {{x_{ij}}} \right)_{m \times n}}$ ,其中 ${x_{ij}}$ 为第j个方案对应的第i个评价指标参数. 通过对所分析的问题进行分解组合, 建立递阶层次分析模型.

2.2 模糊层次分析法权重求解

(1)确定优先关系矩阵

利用三标度法将相邻层次的影响因素进行重要性对比^[9], 得出优先关系矩阵 $F = {\left( {{f_{ij}}} \right)_{m \times m}}$ , 式中:

${f_{ij}} = \left\{ {\begin{array}{*{20}{c}} 0,&{s\left( i \right) < s\left( j \right)} \\ {0.5},&{s\left( i \right) = s\left( j \right)} \\ 1,&{s\left( i \right) > s\left( j \right)} \end{array}} \right.$

(1)

其中, $s(i)$ , $s(j)$ 分别为指标 ${f_i}$ 与 ${f_j}$ 的相对重要性程度.

(2)优先关系矩阵转化为模糊一致矩阵

构建备选方案、制定模糊一致判断矩阵是模糊层次分析法的核心. 若矩阵 $R = {\left( {{r_{ij}}} \right)_{m \times m}}$ 满足: ${r_{ij}} = {r_{ik}} - {r_{jk}}{\rm{ + 0}}{\rm{.5}}$ , 则R为模糊一致矩阵. 通过下面的步骤完成优先关系矩阵到模糊一致矩阵的转化. 对F按行求和, 记为:

${r_i} = \sum\limits_{k = 1}^m {{r_{ik}}}, \quad i = 1,2, \cdots ,m$

(2)

变换得到:

${r_{ij}} = \frac{{{r_i} - {r_j}}}{{2m}} + 0.5,\quad i,j = 1,2, \cdots ,m$

(3)

得到的矩阵R即为模糊一致矩阵.

(3)计算指标权重

采用按行求和归一法来计算指标 ${f_i}$ 对上层因素A的指标权重为:

${w_i} = \frac{{\displaystyle\sum\limits_{k = 1}^m {{r_{ik}}} }}{{\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^m {{r_{ij}}} } }} = \frac{2}{{{m^2}}}\sum\limits_{k = 1}^m {{r_{ik}}}, \;\;\;i = 1,2, \cdots ,m$

(4)

2.3 熵权法修正指标

(1)原始数据标准化

由于评价指标有不同的量纲和数量级, 本文采用负向准则, 使用隶属度函数变换对原始数据作归一化处理, 隶属度函数如下:

${y_{ij}} = \frac{{\max \left( {{x_i}} \right) - {x_{ij}}}}{{\max \left( {{x_i}} \right) - \min \left( {{x_i}} \right)}}\quad $

(5)

式中, ${x_{ij}}$ 是第j个方案的第i个指标的数值. $\max \left( {{x_i}} \right)$ 、 $\min \left( {{x_i}} \right)$ 分别表示第i个准则相对于各方案的最大值和最小值.

以标准化后的数据为基础, 计算评价指标的信息熵, 即:

${e_i} = - k\sum\limits_{j = 1}^n {{p_{ij}}} \ln {p_{ij}},\quad {0 \le {e_i} \le 1}$

(6)

其中,

$k = \frac{1}{{\ln n}}$

(7)

${p_{ij}} = \frac{{{y_{ij}}}}{{\displaystyle\sum\limits_{j = 1}^n {{y_{ij}}} }}$

(8)

若 ${y_{ij}}$ 对于给定的评价指标i全部相等, 则:

${p_{ij}} = \frac{{{x_{ij}}}}{{\displaystyle\sum\limits_{j = 1}^n {{x_{ij}}} }} = \frac{1}{n}$

(9)

此时评价指标的信息熵最大, 取值为:

${e_i} = - k\sum\limits_{j = 1}^n {\frac{1}{n}} \ln \frac{1}{n} = k\ln n$

(10)

(2)计算指标i的偏差指数 ${g_i}$

对于给定评价指标i, ${y_{ij}}$ 的差异性越小, 则 ${e_i}$ 越大, 当 ${y_{i1}} = {y_{i2}} = \cdots = {y_{in}}$ 时, ${e_i} = {e_{\max }} = 1$ , 此时评价指标i几乎无作用. 当 ${y_{ij}}$ 的差异性越大, ${e_i}$ 越小, 故该项指标对于评价对象所起的作用越大. 定义偏差系数向量 $G = ({g_1},{g_2}, \cdots , {g_n})$ , 其中:

${g_i} = \frac{{1 - {e_i}}}{{\displaystyle\sum\limits_{i = 1}^n {1 - {e_i}} }}$

(11)

(3)评价权重修正

利用偏差指数 ${g_i}$ 对前面所求权重进行修正:

$w_i^* = \frac{{{w_i}{g_i}}}{{\displaystyle\sum\limits_{i = 1}^m {{w_i}{g_i}} }}$

(12)

2.4 评价方法

本文使用综合加权评价法确定最优方案. 综合加权评价法是目前应用最为普遍的计算评价指数的方法, 综合考虑各指标对评价因子的影响程度^[10]. 综合评价权重越大, 表示方案越优.

3 基于熵权-模糊层次分析法的清淤泵性能研究

根据桩腿内抽泥系统的工作要求, 从诸多型号的清淤泵中筛选出5种满足工作要求且性能相近的清淤泵型号, 清淤泵的型号及参数如表1所示.

3.1 模糊层次分析法确定初步权重

根据相邻层次之间的影响, 通过两两比较建立了11个优先关系矩阵, 目标层与准则层之间的优先关系矩阵为 $A - {B_i}$ , 如表2所示. 准则层与方案层之间的优先关系矩阵有 ${B_1} - {C_i}$ , ${B_2} - {C_i}$ , …, ${B_{10}} - {C_i}$ . 以 ${B_1} - {C_i}$ 为例建立准则层与方案层的优先关系矩阵, 如表3所示.

基于模糊层次分析法将各优先关系矩阵转成模糊一致矩阵, 并根据式(4)求得如表4所示的准则层的评价权重.

3.2 熵权法修正权重

熵权法是根据同一指标观测值的差异度对指标进行赋权, 观测值差异越大则指标权重越大, 即熵权法完全取决于观测值数据, 是一种客观赋权法^[11]. 熵权法求权重步骤如下:

首先, 对初始数据进行标准化处理, 消除各参数中量纲与数量级的影响; 其次, 将参数代入式(6)与式(7)中分别求得熵与偏差指数; 最后利用得到的偏差指数对模糊层次分析法的权重进行修正, 计算得到清淤泵各指标的准则层评价权重如表5所示.

3.3 加权综合评价

将熵权修正后的准则层的评价权重向量与方案的评价权重向量作内积, 得到方案层的综合评价权重, 计算公式如下:

${Q_i} = {W_{A - {C_i}}} = W_{_{A - {B_i}}}^*W_{_{{B_i} - {C_i}}}^{\rm{T}}$

(13)

其中, ${Q_i}$ 为第 $i$ 个方案的综合指标权重, $0 \le {Q_i} \le 1$ , ${Q_i}$ 越大表示方案越优; $W_{^{_{A - {B_i}}}}^*$ 为熵权修正后的准则层的评价权重向量; $W_{^{_{{B_i} - {C_i}}}}^{\rm{T}}$ 为模糊层次分析法得到的方案层相对评价权重向量的转置. 采用熵权-模糊层次分析法得到的综合评价指标权重如表6所示.

3.4 结果分析

根据表6可知, NSQ100-60-45型清淤泵在所有配置方案中综合评价权重最高, NSQ100-60-45为5种配置方案中的最优配置方案.

结合表4与表5分析可知, 流量及扬程始终排在第1、2位, 说明清淤泵的流量及扬程始终为其选型的过程中的主要考虑因素; 在模糊层次分析法的评价权重中, 维修周期与使用寿命的权重排序相同, 经过熵权耦合后, 维修周期的评价权重有所下降, 说明使用寿命在清淤泵的选择中更受重视, 熵权耦合后的评价指标权重更能有效的区分出评价指标体系中各指标的重要性.

本文利用偏差指数对模糊层次分析法的权重进行修正, 既保证了重要指标所占的权重, 又使得权重兼顾了主观性与客观性; 修正后的评价权重更加精确合理, 有效的提高了各指标重要性的区分度, 避免了各评价指标因差异性小而造成的不合理现象.

4 结语

(1)熵权修正后的模糊层次分析法更贴近实际工作需要, 适用于具有复杂属性的目标优化决策选型.

(2)将熵权-模糊层次分析法应用于清淤泵配置选型, 基于对模糊因素的考虑, 强化了问题分析突出点, 有效区分了清淤泵评价体系中各评价指标的重要性, 提高了配置方案的科学性和客观性.

(3)清淤泵是桩腿内清淤系统的核心设备之一, 其配置方案的选择对桩内抽泥系统具有重要意义. 从评价结果看, NSQ100-60-45型清淤泵具有使用寿命长、扬程较高、体积小、价格适中的特点, 更适用于桩腿内抽泥系统.