2. 四川省气象局, 成都 610072;
3. 中国科学院 大气物理研究所, 北京 100029
2. Sichuan Provincial Meteorological Service, Chengdu 610072, China;
3. Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China
基于卫星多波段数据融合算法, 将多传感器和多信息源的数据、信息加以联合、相关和组合, 以获得精确的位置估计和一致性估计. 基本策略是由低层到高层对多源信息进行整合、抽象的信息处理过程[1]. 通过多源信息的互补, 消除观测对象的不确定性、减小数据冗余, 可改善待观测对象的精确性和定量可靠性, 从而有效提高数据利用率.
现有融合算法主要有以下几类[1]:
(1)彩色空间变换融合法. 将低分辨率的RGB影像数据经过变换映射至HIS空间, 然后采用特定的融合算法使其与高分辨率数据进行融合处理, 进而置换相应的部分, 最后经过逆变换重构融合数据. 根据映射的颜色空间不同, 彩色空间融合法可分为HIS变换、YIQ变换、HLS变换融合法等.
(2)加权融合或基于信息量的融合. 可根据经验值或相关系数设置权重函数, 以减少冗余. 此算法的优点在于简单易行, 可结合基于特征的融合方法, 针对不同要求, 灵活改变信息特征提取方法.
(3)高通滤波融合(High-Pass Filter, HPF). 通过将高分辨率数据中的几何信息逐像素叠加到低分辨率数据中而进行. 先对高分辨率的全色数据和低分辨率的多光谱数据各波段进行直方图匹配, 对匹配后的全色数据进行高通滤波, 再将其加入多光谱的各个波段, 最后将多光谱各个波段的数据进行彩色合成.
(4)主成分变换融合(Principal Component Analysis, PCA). 通过该变换, 使多光谱数据在各波段具有统计独立性, 便于在各波段采用相应的融合策略.
(5)小波融合(Wavelet Transforms, WT). 小波变换作为新兴的数学分析方法日益受到广泛重视, 是分析和处理非平稳信号的一种有效工具. 小波变换以局部化函数所形成的小波基作为基底而展开, 是一种窗口大小固定不变但其形状可改变的时频局部化分析方法. 它已在图像编码领域、计算机视觉、语音信号处理等领域取得了突破性进展.
在小波融合算法中, 最常用到二进制小波变换, 常用来处理来自同一传感器的遥感数据, 通过对数据进行分解、重构, 在高、低频采用相应的融合策略来实现数据融合[2]. 但在实际应用中, 常需要融合来自不同传感器的数据, 需要扩展到多进制小波算法, 但为保证融合处理速度, 小波分解的阶数取得并不高, 这时融合结果空间细节的表现受到影响. 考虑到HSV融合法能突出空间信息表达能力、小波包融合法能克服小波变换对高频信息处理的缺陷, 所以构建两种改进算法: 基于HSV的小波融合法和基于区域特征的自适应小波包融合算法分别实现不同传感器的数据融合.
1 基于HSV的多进制小波融合(HSV-WT)多进制小波可理解为频率域的分解问题, 二进制小波把频率域分解成两个通道, 多进制小波把频率域分解成多个通道, 分别对每个分解层次的低、高频部分按各自的融合策略进行处理, 综合各组数据的特征信息, 最后根据多进制小波重构公式进行小波逆变换, 重构融合数据[3]. 因此它能突破待融合数据的分辨率比值限制, 实现分辨率之比非2n的数据融合.
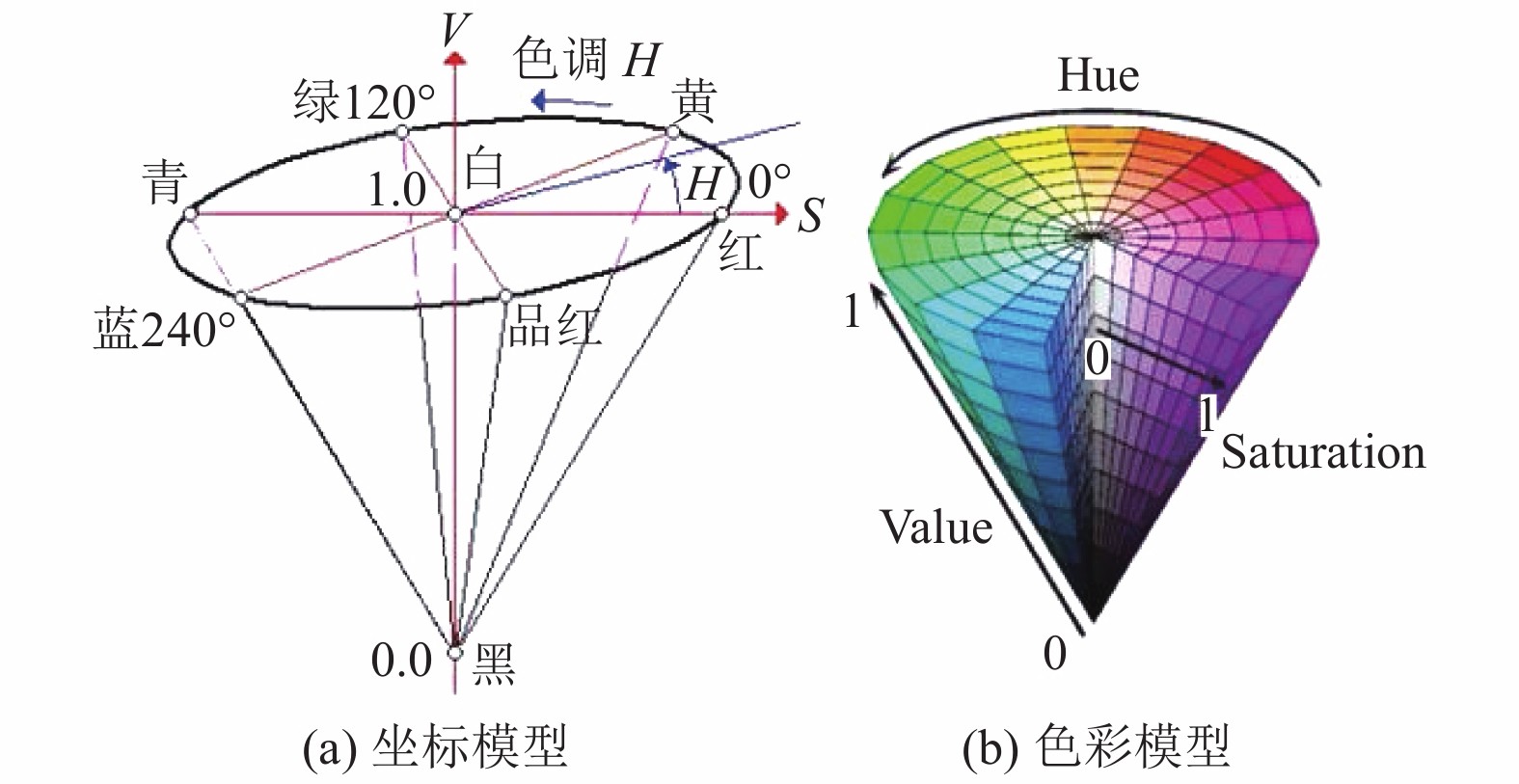
1.1 HSV融合法HSV分别代表 Hue (色调)、Saturation (饱和度)、Value (亮度), 融合模型为一圆锥体, 如图1所示, 圆锥底面对应色调H, 表示所处的颜色位置, 以绕V轴的旋转角度来表示不同颜色, 0°对应红色, 120°对应绿色, 240°对应蓝色, 互补色之间相差180°; 饱和度S从低到高表示为由轴心向锥体圆周过渡, 表示所选颜色的纯度和该色最大纯度之间的比率, 范围为0–1. 当S=0时, 只有灰度; 明度V表示色彩明亮程度, 范围为0–1[4,5].
|
图 1 HSV变换模型 |
从RGB空间转换到HSV空间[6]: 首先, 归一化RGB色彩空间的值, 求其最大值和最小值.
令
| $\left\{\begin{split} &{H = \left\{ {\begin{array}{*{20}{l}} {60\left( {G - B} \right)/\left( {m - n} \right)},&{R = m{\text{且}}G \ge B}\\ {360 + 60\left( {G - B} \right)/\left( {m - n} \right)},&{R = m{\text{且}}G < B}\\ {120 + 60\left( {B - R} \right)/\left( {m - n} \right)},&{G = m}\\ {240 + 60\left( {R - B} \right)/\left( {m - n} \right)},&{B = m}\\ 0,&{S = 0} \end{array}} \right.}\\ &{S = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{m - n}}{m}},&{m \ne 0}\\ 0,&{m = 0} \end{array}} \right.}\\ &V = m \end{split}\right.$ | (1) |
由于各传感器通过的光路不同或成像机制不同等原因, 多源遥感数据间可能出现相对平移、旋转或比例缩放等现象, 必须先对图像进行配准. 配准的关键在于从多个图像中找到具有共性特征的控制点, 包括相对配准和绝对配准[1].
(1)相对配准: 先在两幅待配准图像上选择同名控制点, 用二次多项式模型建立两个同名像素的关系, 最后重采样成相同分辨率的图像.
(2)绝对配准: 在统一地理坐标系下对待配准图像进行几何纠正, 常用多项式纠正法, 再重采样为相同分辨率图像.
多项式纠正法的关键是采用一定数量的具有空间坐标的地面控制点, 利用这些点对应的坐标, 通过平差原理计算多项式系数, 数学模型如下[7]:
| $\left\{ \begin{split} x=&{a}_{0}+\left({a}_{1}X+{a}_{2}Y\right)+\left({a}_{3}{X}^{2}+{a}_{4}XY+{a}_{5}{Y}^{2}\right) \\ &+ \left({a}_{6}{X}^{3}+{a}_{7}{X}^{2}Y+{a}_{8}{XY}^{2}+{a}_{9}{Y}^{3}\right)+\cdots \\ y=&{b}_{0}+\left({b}_{1}X+{b}_{2}Y\right)+\left({b}_{3}{X}^{2}+{b}_{4}XY+{b}_{5}{Y}^{2}\right) \\ &+\left({b}_{6}{X}^{3}+{b}_{7}{X}^{2}Y+{b}_{8}{XY}^{2}+{b}_{9}{Y}^{3}\right)+\cdots \end{split}\right. $ | (2) |
式中,
| $ N=\dfrac{(n+1)(n+2)}{2} $ | (3) |
根据上式计算多项式系数:
|
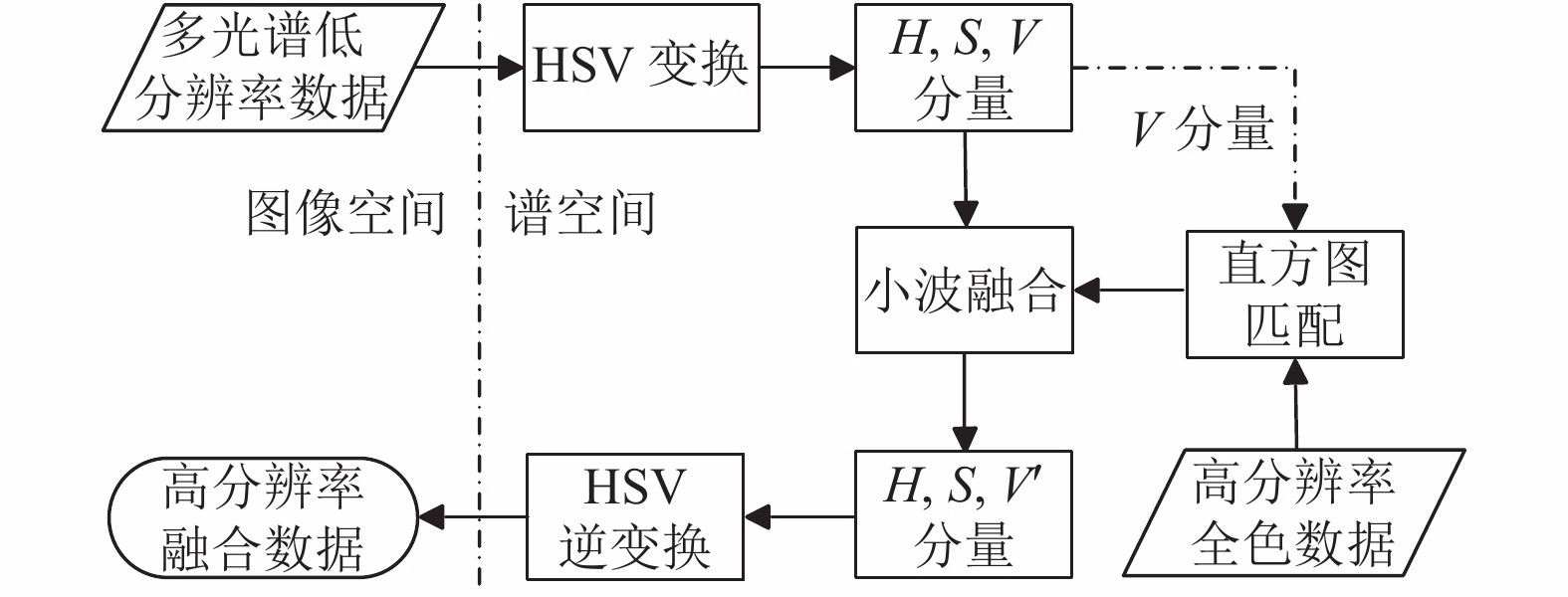
图 2 基于HSV的小波融合法实现框图 |
(1)将待融合的高分辨率数据
(2)将低分辨率多光谱数据
(3)将V分量和高分辨率数据
(4)利用多进制小波融合算法对V分量信息和高分辨率数据
(5)将得到的V'分量和前面的H、S分量数据进行HSV逆变换, 输出高分辨率的融合后数据.
2 基于区域特征的自适应小波包融合算法(AWP)小波包融合算法通过对不同分辨率的高频部分进一步划分, 进行递归分解, 突出高分辨率数据的细节层次信息. 该算法能突出细节区域特征, 且采用自适应算法, 故称之为基于区域特征的自适应小波包融合算法[12](Adaptive Wavelet Packet based on region features, AWP).
2.1 算法介绍多分辨率分析可以对信号进行有效的时效分解, 但由于其尺度函数时按二进制变化的, 因此在高频段其频率分辨率较差, 只能对信号的频段进行指数等间隔划分. 小波包分解为信号提供一种更加精细的分解方法, 通过把频带进行多层次划分, 对多分辨分析中没有细分的高频部分进一步分解, 并根据被分析信号特征, 自适应地选择相应频段, 使之与信号频谱相匹配, 从而提高时频分辨率, 因此具有更广泛的应用价值[13].
这种算法可同时对数据的高、低频部分进行任意尺度的递归分解和融合处理, 克服了传统小波融合算法对高分辨率数据高频细节信息处理的不足, 突出高分辨率数据细节层次信息, 获取高分辨率的多光谱融合数据, 从而提高数据可用度和研究对象解译的可靠性[1].
2.2 算法实现首先对配准的遥感数据进行小波包分解, 分解时, 对上一层的各高、低频部分进行全方位递归分解, 采用基于自适应能力和区域特征的融合策略对子数据融合, 最后逆变换重构数据. 一般情况下, 小波包分解层次越多, 融合结果中包含的细节信息就越丰富. 但随着分解层次的增多, 计算量增加, 而且易造成顶层融合数据损失增大[14]. 因此折中考虑两点, 一般分解层次取3–5之间. 本文的分解层次取3, Haar小波基.
如图3, 基于自适应能力和区域特征的融合策略为: 按照不同融合策略分别对每一级小波系数上的高、低频信息进行处理, 并合并系数. 加权平均法的基本原理是[1]:
| $ {C}_{F}\left({{m}},{{n}}\right)=\alpha \times{C}_{A}\left({{m}},{{n}}\right)+(1-\alpha )\times{C}_{B}\left({{m}},{{n}}\right) $ | (4) |
其中,

|
图 3 融合策略 |
平均梯度法的融合规则为[1]: 利用该像素的局部平均梯度确定融合后高频子数据的像素值. 设待融合数据为
| $\left\{ \begin{split} & {\text{当}}{{G}}{A}_{j}^{k}\left({{x}},{{y}}\right)>G{B}_{j}^{k}\left({{x}},{{y}}\right) {\text{时}}, \;\;{F}_{j}^{k}\left({{x}},{{y}}\right)={{G}}{A}_{j}^{k}\left({{x}},{{y}}\right) \\ &{\text{当}} {{G}}{A}_{j}^{k}\left({{x}},{{y}}\right)<G{B}_{j}^{k}\left({{x}},{{y}}\right) {\text{时}}, \;\;{F}_{j}^{k}\left({{x}},{{y}}\right)={{G}}{B}_{j}^{k}\left({{x}},{{y}}\right) \end{split}\right. $ | (5) |
最后使用重构滤波器逆向逐层二插值重构数据, 获取融合后数据.

|
图 4 基于区域特征的自适应小波包融合法 |
算法步骤具体说明如下:
(1)输入高分辨率的全色数据和多光谱数据.
(2)初始化分解系数、分解层次数目等参数.
(3)设计尺度函数
(4)根据小波包分解算法, 使用分解滤波器逐层抽样分解全色和多光谱数据, 获取高、低频分解数据.
(5)对小波包分解后的多光谱数据和全色数据进行融合. 采用基于区域特征的自适应小波包融合算法, 通过直方图均衡化, 求分解窗口的方差、能量和信息熵, 计算像素权值, 按照公式获取融合子数据.
设小波分解后的多光谱数据为
对三波段的子数据
| $ {S}_{i}=-{\sum }_{i=0}^{L}P\left(i\right){{log}}_{2}P\left(i\right) $ | (6) |
其中,
| $ {D_i} = \frac{{\displaystyle\sum _{i = 0}^{M - 1}\displaystyle\sum _{j = 0}^{N - 1}{{\left[ {G(i,j) - \bar G} \right]}^2}}}{{MN}} $ | (7) |
其中,
| $ {E}_{i}=-{\sum }_{i,j\in Z}^{N-1}P\left[i\right]\left[j\right]G(i,j) $ | (8) |
其中,
| $ P\left[i\right]\left[j\right]=\left\{\right\{0, 1, 0\}, \{1, 2, 1\}, \{0, 1, 0\left\}\right\}\text{. } $ |
计算子数据
| $ {W}_{i}=a\times {E}_{i}+b\times {D}_{i}+c\times {S}_{i} $ | (9) |
其中,
按照式(10)获取融合后数据
| $ {F}_{j}^{k}(x,y)=\dfrac{{A}_{j}^{k}(x,y) \cdot {W}_{a}+{B}_{}^{k}(x,y) \cdot {W}_{b}}{{W}_{a}+{W}_{b}} $ | (10) |
(6)根据上述的小波包重构滤波器逆向逐层插值重构数据, 获取融合后数据.
3 数据介绍 3.1 多光谱LandSat TM数据LandSat是美国陆地探测卫星系统, TM (Thematic Mapper)是LandSat-4、LandSat-5携带的专题绘图仪[17], LandSat TM波段信息如表1所示. 本文采用Level 1T 标准地形校正产品, 选用Band 4、Band 3、Band 2进行融合, 有利于分辨植被、土壤和道路等信息[18].
| 表 1 LandSat TM波段信息 |
3.2 全色SPOT-5数据
SPOT卫星是法国空间研究中心(CNES)研制的地球观测卫星系统, SPOT-5星上载有2台高分辨率几何成像装置(HRG)、1台高分辨率立体成像装置(HRS)、1台宽视域植被探测仪(VEG)等, 前后模式实时获得立体像对[19], 其波段信息如表2所示. 本文选用SPOT-5星的全色波段PAN的10 m分辨率HRS数据.
| 表 2 SPOT-5卫星的波段信息 |
3.3 合成孔径雷达SAR数据
合成孔径雷达SAR (Synthetic Aperture Radar) 采用搭载在飞机或卫星上的移动雷达, 达到和大型天线同样精度的雷达系统. 特点是分辨率高, 能全天候工作, 能有效地识别伪装和穿透掩盖物[20]. 本文选用欧洲空间局的ERS-2 (the second European Remote sensing Satellite) 雷达数据, 平均轨道高度为780 km, 其参数如表3所示[20].
4 结果分析本文采用HSV-WT、AWP算法对两组数据进行处理, 选取的滤波器窗口为3×3, 小波变换法采用了3层小波分解和重构算法, Haar小波基.
4.1 多光谱LandSat TM数据和全色SPOT数据融合采用HSV-WT和AWP对两组数据进行融合.
4.1.1 读取源数据先选择TM的Band 3与SPOT进行配准, 可发现两图左边部分的山脉区域清晰可见, 图5(b)中有一块白色云区.
4.1.2 数据配准校正将图5(a)作为基准数据, 对图5(b)数据进行校正. 通过控制点位法进行相对配准, 再通过二次多项式纠正法进行绝对配准, 如图6所示. 同理校正另外两个波段数据.
| 表 3 合成孔径雷达成像模式特性参数 |

|
图 5 源数据 |
采用多项式纠正法时, 误差如表4. 由表4所知, 采用一次多项式纠正时误差较大, 因为一次项纠正仅对旋转、平移、缩放带来的误差进行了纠正, 并没有对非线性变化引起的误差进行改正. 采用二次多项式时, 中误差明显变小, 不仅纠正了线性变形, 还进一步改正了非线性变形.
4.1.3 融合TM Band 4、Band 3、Band 2采用二进制小波变换法融合校正后的TM三通道数据, 如图7所示.

|
图 6 校正后的TM Band 3 |
| 表 4 多项式纠正误差(单位: m) |

|
图 7 TM Band 4、Band 3、Band 2融合结果 |
分析融合结果, 左边区域为山脉, 左边有一块白色区域为云, 旁边与其形状相似的黑色区域为云影. 卫星观测的角度以及山脉的凸凹不平等因素导致云和云影之间的位置差异; 深色区域为水体.
4.1.4 融合TM和SPOT数据分别采用HSV-WT、AWP对图5(a)和图7进行融合, 如图8所示.
4.1.5 融合评价观察图8发现, 使用两种方法融合后的结果既融入了全色SPOT数据的细节信息, 又保留了TM数据的光谱信息. 融合后数据在保持光谱信息和增强空间信息两方面得到提高. 对比图8(a)、图8(b)发现, 图8(a)的光谱失真较大, 视觉效果不如图8(b). 在图8(b)中, 山脉的纹理特性和右边部分的细节特征更加丰富, 更有利于地物判别. 比较两种融合结果的性能参数如表5.

|
图 8 融合结果 |
| 表 5 TM和SPOT融合后数据的参数结果 |
从表5可看出, 融合结果图8(a)、图8(b)在多光谱TM数据的基础上, 提高了方差, 其信息熵和清晰度都比源数据大; 对比融合结果图8(a)、图8(b), 在方差、信息熵、清晰度和相关指数4项指标上, 图8(b)较大, 且图8(b)的扭曲程度、偏差指数较小. 说明采用AWP方法较HSV-WT法更优, 采用AWP法处理过的图像更加清晰, 纹理信息更丰富, 对象的几何特征更完整.
4.1.6 融合另一组伦敦地区数据对另一组伦敦地区的数据采用相同方法进行处理, 选用TM的R、G、B波段合成彩色影像.
图9(a)采用TM的R、G、B波段融合表示彩色图像, 图像色彩更接近自然色彩, 更符合人的视觉特性. 图中, 黑色区域为水体, 绿色区域为地表. 放大观察图9(c)、图9(d), 图像的细节信息得到明显改善, 光谱信息的增加提高地物的纹理特性. 目视观察比较图9(c)、图9(d), 图9(d)的色彩更为自然, 纹理细节更丰富, 目视效果更加清楚. 表6列出图9融合结果的性能参数,
综合比较, 图9(d)数据优于图9(c), 说明采用AWT效果较好.

|
图 9 伦敦地区的数据融合结果 |
| 表 6 图9融合后数据的参数结果 |
4.2 多光谱LandSat TM数据和SAR数据融合
对意大利罗马地区的TM和ERS-2 SAR数据进行融合, 使用AWP实现.
4.2.1 读取源数据读取罗马地区的源数据, 将TM Band 4、Band 3、Band 2进行二进制小波融合, 如图10所示, SAR数据有一定的立体视觉性, 图10(b)中黑色区域为水体.

|
图 10 意大利罗马地区的源数据 |
4.2.2 数据配准
将图10(a)的SAR数据作为基准数据, 对图10(b)进行校正. 校正法同上, 图11所示为校正后的TM数据.
4.2.3 数据融合由4.1.5节和4.1.6节知, 基于自适应小波包融合算法较优, 故采用此算法融合图10的SAR数据以及图11的校正后TM数据, 融合结果如图12.

|
图 11 校正后的TM数据 |
4.2.4 融合评价
由图12, 融合后影像具有SAR数据的立体视觉性, 在融入TM的光谱信息后, 增加了纹理的清晰度, 有助于进一步区分地表的覆盖类型. 表7列出图12融合结果的性能参数,
由表7知, 融合后的方差、信息熵均高于源数据, 说明融合丰富了信息量. 融合后的清晰度提高较为明显, 说明融合后数据增强了细节特征.

|
图 12 SAR和TM融合结果 |
| 表 7 图12融合后数据的参数结果 |
4.3 与其他融合算法的对比分析
基于4.1.1节的多光谱LandSat TM数据和全色SPOT数据, 分别采用常用融合算法HSV变换、主成分变换(PCA)、多进制小波变换(WT)对同一组数据进行融合, 与采用本文算法HSV-WT、AWP的融合结果进行比较, 如表8所示.
从表8可看出,融合结果均在TM数据的基础上, 提高了方差, 其信息熵和清晰度都比源数据大; 对比各项参数, 本文算法AWP、HSV-WT在各项指标上, 均优于其他3种传统算法, 验证了本文改进算法的有效性.
| 表 8 不同融合算法的参数结果 |
5 结论
本文将低分辨率数据的多光谱信息、全色数据的高分辨率信息或SAR数据的高空间信息有机结合起来, 关注在尽可能保持原光谱信息的同时, 提高融合结果的空间分辨率. 主要结论如下:
(1)两种改进算法均优于传统融合算法, 融合后的数据在保持光谱信息和提高空间细节信息两方面均得到提高. 这两种算法相对传统小波算法, 能克服对高频信息处理的缺陷, 突破待融合数据的分辨率比值限制, 实现分辨率之比非2n的数据融合.
(2) HSV-WT将HSV的空间信息表达能力与多进制小波变换的良好局部化性质有机结合, 从而使融合后的数据在保持光谱信息和提高空间分辨率两方面的综合性能达到平衡. 实验证明此方法简单有效, 融合结果既融入了SPOT数据的细节信息, 又保留了TM数据的光谱信息.
(3) AWP克服小波变换容易受分解阶数影响的缺陷, 对高频部分进一步划分, 通过递归分解突出高分辨率数据的细节层次信息. 用此方法处理两组数据, 效果优于HSV-WT.
(4)下阶段应进一步探讨针对要突出的不同特征, 怎样选取波段组合; SAR数据具有穿透云层、植被的能力, 它所获得的信息取决于物体的几何特性和介电特性, 可思考怎样发挥其优点, 最大限度地提取地物特征信息.
| [1] |
张永生, 戴晨光, 张云彬, 等. 天基多源遥感信息融合——理论、算法与应用系统. 北京: 科学出版社, 2005.
|
| [2] |
刘春, 陈能. 基于小波变换的快鸟遥感影像数据融合. 同济大学学报(自然科学版), 2004, 32(10): 1371-1375. DOI:10.3321/j.issn:0253-374X.2004.10.021 |
| [3] |
张爱明, 李乃强. 多源遥感影像小波融合方法研究与分析. 现代测绘, 2009, 32(5): 39-41. DOI:10.3969/j.issn.1672-4097.2009.05.013 |
| [4] |
焦竹青, 徐保国. HSV变换和同态滤波的彩色图像光照补偿. 计算机工程与应用, 2010, 46(30): 142-144. |
| [5] |
石智, 张卓, 岳彦刚. 基于Shearlet变换的自适应图像融合算法. 光子学报, 2013, 42(1): 115-120. |
| [6] |
秦绪佳, 程燕飞, 范颖琳, 等. 基于三边滤波的HSV色彩空间Retinex图像增强算法. 小型微型计算机系统, 2016, 37(1): 168-172. DOI:10.3969/j.issn.1000-1220.2016.01.032 |
| [7] |
李雷, 陈福江, 李峰. 环渤海地区TM影像图制作. 北京测绘, 2012(5): 60-63. DOI:10.3969/j.issn.1007-3000.2012.05.016 |
| [8] |
李卫红, 周平华, 李琦, 等. “资源一号”02C卫星影像几何校正方法试验. 华北科技学院学报, 2015, 12(1): 99-102. |
| [9] |
王蕾, 杨武年, 任金铜, 等. GF-2卫星影像在土地变更监测中的适用性及潜力分析. 航天返回与遥感, 2017, 38(4): 96-105. DOI:10.3969/j.issn.1009-8518.2017.04.012 |
| [10] |
张大明, 李璐, 符茂胜, 等. 基于小波变换的全色和多光谱遥感图像融合. 国土资源遥感, 2008, 20(1): 50-54. |
| [11] |
常化文. 基于HSV变换与àtrous变换的图像融合. 计算机工程与设计, 2009, 30(4): 938-940. |
| [12] |
董广军, 张永生, 戴晨光. 高分辨率遥感影像融合处理技术的对比分析研究. 光学技术, 2006, 32(6): 827-830. DOI:10.3321/j.issn:1002-1582.2006.06.020 |
| [13] |
周伟, 桂林, 周林, 等. MATLAB小波分析高级技术. 西安: 西安电子科技大学出版社, 2006.9.
|
| [14] |
董广军, 张永生, 范永弘. PHI高光谱数据和高空间分辨率遥感图像融合技术研究. 红外与毫米波学报, 2006, 25(2): 123-126. DOI:10.3321/j.issn:1001-9014.2006.02.010 |
| [15] |
钱国栋, 邹珍军, 许宁. 遥感图像多模型融合处理与分析. 北京测绘, 2014(5): 19-25. DOI:10.3969/j.issn.1007-3000.2014.05.006 |
| [16] |
Hall DL, Llinas J. An introduction to multisensor data fusion. Proceedings of the IEEE, 1997, 85(1): 6-23. DOI:10.1109/5.554205 |
| [17] |
姚磊. 基于支持向量机的遥感影像分类研究[硕士学位论文]. 济南: 山东师范大学, 2012.
|
| [18] |
周亦, 胡琨菠, 张亚亚. 资源一号02C与SPOT5在土地调查监测应用中的对比分析. 北京测绘, 2015(6): 43-47. DOI:10.3969/j.issn.1007-3000.2015.06.011 |
| [19] |
王彩霞. 也论现代测绘定位技术. 科技论坛, 2009(35): 20. |
| [20] |
Roy DP, Ju J, Lewis P, et al. Multi-temporal MODIS-Landsat data fusion for relative radiometric normalization, gap filling, and prediction of Landsat data. Remote Sensing of Environment, 2008, 112(6): 3112-3130. DOI:10.1016/j.rse.2008.03.009 |
 2021, Vol. 30
2021, Vol. 30



