2. 中国科学院 沈阳计算技术研究所, 沈阳 110168;
3. 阜新市生态环境保护服务中心, 阜新 123100;
4. 辽宁省医疗器械检验检测院, 沈阳 110000
2. Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China;
3. Fuxin Ecological Environmental Protection Service Center, Fuxin 123100, China;
4. Liaoning Medical Device Test Institute, Shenyang 110000, China
随着时代飞跃的发展和提高, 人们的生活水平越来越好, 城市的扩张, 以及工业化的腾飞, 对环境的影响是越来越大. 人们慢慢将环境资源的可持续发展作为茶余饭后的话题[1], 尤其是人类生存所必须的水资源, 水资源中的污染物浓度值亦不可忽视, 污染物个数多达数十种. 因此, 伴着社会的发展, 水环境质量的分析, 是完成环境与经济的可持续发展的重要工作. 相关部门对水资源的管理和监测也越来越重视, 对各个流域的水质有着周期性的监测, 但随着环境质量的变化, 水质也会跟随着变化, 主要体现在: (1) 比如扩建, 那原地点的水质就会发生改变. (2) 比如某一处土地集中进行绿化, 那么土壤的质量必然会随着变化, 这就必定导致水质量的变动. 所以各个流域监测点位都是要随着时间, 伴着周围环境质量和土壤的质量的变化而变化的. 那么就必然涉及到点位优化的进行. 这对实时监测水质最新的动向很有意义, 也让把控着水质的动向, 对水资源更好的治理和监测[2].
水质监测过程中, 点位越多, 收集的信息就越多, 越能详细反映出水中污染物的真实状况. 然而, 碍于监测所需要的人力、资金、设备等成本的限制, 无法对区域水质进行全面, 无死角的布点监测. 因此, 为了能得到具有代表性又具有经济性的监测点位, 就需要对大气监测点进行优化处理. 本文就是采用auto-encoder结合聚类进行水质监测的点位优化. 遵循了监测点位优化的宗旨: 以尽量少的数据, 尽可能的代表全部的监测点位的数据.
1 研究方法根据要优化监测点位这一目的, 选用了聚类方面的算法, 由于是运用在水质监测方面, 那么选取了适用于水质、地质、农业、天气方面的聚类算法. 由于样本中高纬度的数据特征, 存在各种噪声, 如果不先剔除掉多余的特征和噪声, 模型的效果会受到很大影响, 但是如果只是单纯的剔除某些特征, 那么就会把特征之间的联系给抹掉, 聚类的结果不理想. 为了解决此问题, 本文采用了在聚类之前, 先用神经网络降维的方法进行特征降维, 将样本中原有的特征降维, 重新生成一个更低维度的新样本[3-6]. 但同时特征降维涉及到有效数据的完整性, 对于高纬度的水质监测点位数据, 需要将有效的数据保存到降维后的数据中, 剔除无效的数据. 由于数据样本不需要进行标记, 这里采用了无监督学习的auto-encoder神经网络[7-9]. 对于水质点位监测的数据, 传统的PCA方法因为其线性降维, 另外PCA方法更依赖初始的数据, 不能很好的保留有效信息的完整性, 相对来讲, 自编码器可以学习非线性关系, 有效数据的保留更加充分, 同时剔除无效的数据, 泛化能力更强. 图1为研究方法的整体流程图.
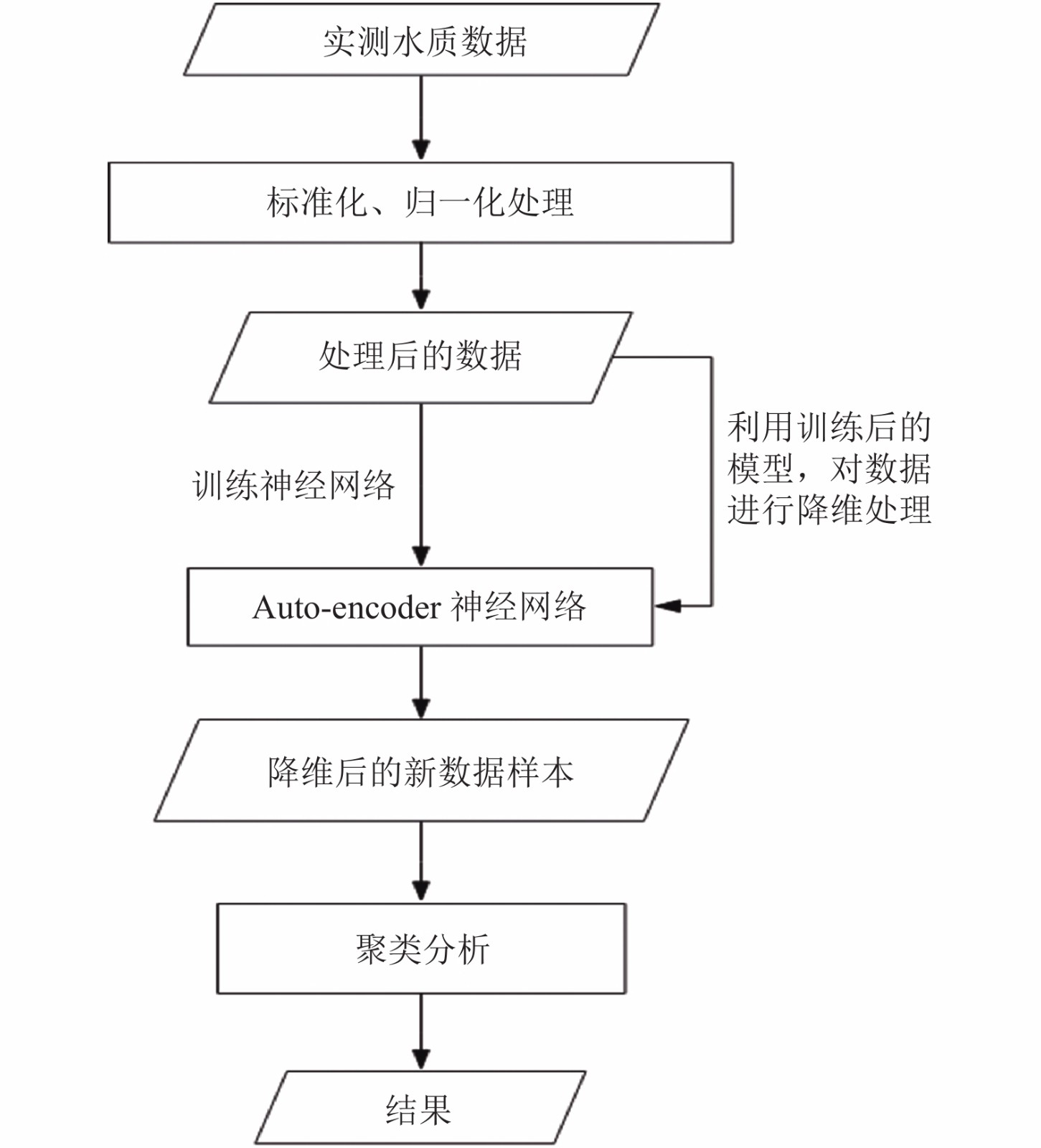
|
图 1 研究方法流程图 |
1.1 自编码器auto-encoder神经网络
Auto-encoder是神经网络的一种, 也是最常见的深度学习算法之一[10-13], 其结构如图2所示. Auto-encoder主要被用来降维和特征提取, 另外该神经网络属于无监督学习, 不需要标记训练数据, 这也是本文采用此种方法的原因[14].
自动编码器包括三层神经网络, 第一部分是输入层, 第二部分是隐藏层, 隐藏层可以为多层, 第三部分是输出层, 输入层n个神经元对应样本中的特征, 隐藏层k(k<n)个神经元是所需要降到的维数, 输出层是和输入层结构完全一致. 从输入层到隐藏层的传递叫编码过程, 提取特征, 压缩数据的维度, 从隐藏层到输出层的传递叫解码过程, 从而进行数据的重构, 通过重构的数据和输入的数据之间的误差来更新各层之间的权重和偏置, 为的是让输出层尽量和输入层一致. 通过函数表达式来表示, 由两部分组成, 一个编码器hide=f(input), 一个解码器output=g(hide), 最后使得input约等于g(f(input)).
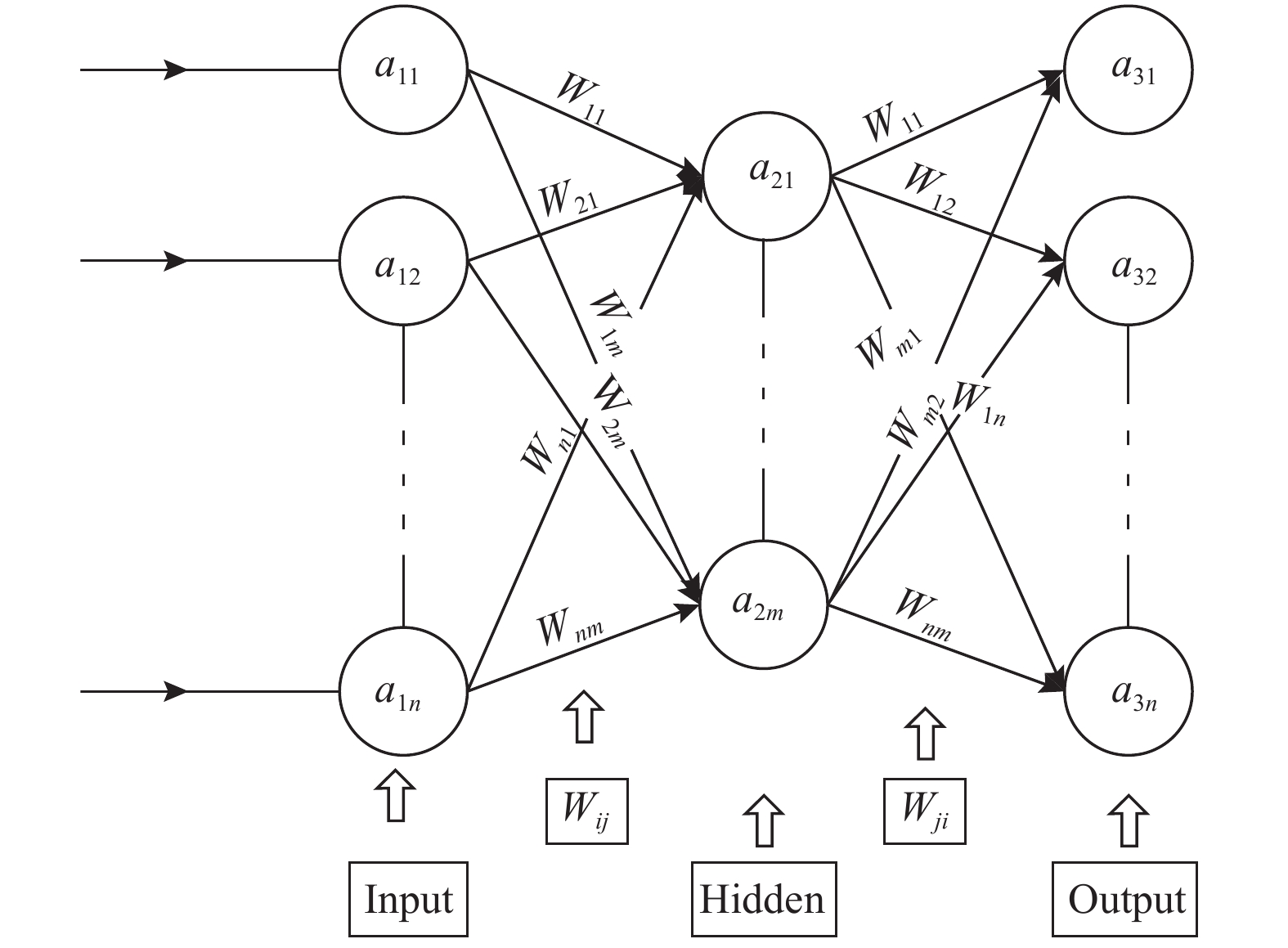
|
图 2 Auto-encoder神经网络结构示意图 |
输入层节点
输入层和隐藏层之间计算:
| ${Z^1} = {a^1}{W_{ij}} + {b^2}$ | (1) |
| $a_j^2 = f\left( {{Z^1}} \right)$ | (2) |
在隐藏层和输出层之间计算:
| ${Z^2} = {a^2}W_{ji}^{\rm{T}} + {b^3}$ | (3) |
| $a_i^3 = f\left( {{Z^2}} \right)$ | (4) |
其中, f是激活函数, 本文选择Sigmoid激活函数:
| $f\left( x \right) = {1 / {\left( {1 + {e^{ - x}}} \right)}}$ |
输出层
取误差公式:
| $E = \frac{1}{2}\sum\limits_{i = 1}^n {{{\left( {a_i^1 - a_i^3} \right)}^2}} $ |
记
| $E = \frac{1}{2}\sum\limits_{i = 1}^n {{\ell _i}^2} $ | (5) |
对权重进行链式求导并更新:
| $\left\{ \begin{split} \dfrac{{\partial E}}{{\partial {W_{ji}}}} = &\dfrac{{\partial a_i^3}}{{\partial {W_{ji}}}} \cdot \dfrac{{\partial {\ell _i}}}{{\partial a_i^3}} \cdot \dfrac{{\partial E}}{{\partial {\ell _i}}}\\ {W_{ji}} = &{W_{ji}} + \eta \left( { - \dfrac{{\partial E}}{{\partial {W_{ji}}}}} \right)\\ {W_{ji}} =& {W_{ji}} + \eta {a^2}{\ell _i} \end{split}\right. $ | (6) |
由于输入层到隐藏层的权重参数矩阵和隐藏层到输出层的权重参数矩阵互为转置关系, 因此, 只需要把后者的权重转置赋值到前者.
对偏置
| $\left\{ \begin{split} \dfrac{{\partial E}}{{\partial {b^3}}} =& \dfrac{{\partial E}}{{\partial {b^3}}} \cdot \dfrac{{\partial {\ell _i}}}{{\partial {a^3}}} \cdot \dfrac{{\partial E}}{{\partial {\ell _i}}}\\ {b^3} =& {b^3} + \eta {\ell _i} \end{split}\right. $ | (7) |
对偏置
| $\left\{ \begin{split} \frac{{\partial E}}{{\partial {b^2}}} =& - {a^2}\left( {1 - {a^2}} \right) \cdot \sum\limits_{i = 1}^n {{W_{ji}} \cdot {\ell _i}} \\ {b^2} =& {b^2} + \eta {a^2}\left( {1 - {a^2}} \right)\sum\limits_{i = 1}^n {{W_{ji}} \cdot {\ell _i}} \end{split}\right. $ | (8) |
式中,
整个auto-encoder算法伪代码如算法1.
算法1. Auto-encoder
1. 初始化auto-encoder中各层之间的连接权重、偏置和学习速率.
2. for all 数据集中每一个样本do
3. while (对于当前样本) do
4. 根据式(1), 式(2)计算隐藏层的输出值;
5. 根据式(3), 式(4)计算输出层的输出值;
6. 根据式(5)计算输入层和输出层的误差;
7. if (达到停止条件)
8. break;
9. else if
10. 根据式(6)~式(8)更新权值和偏置;
11. end if
12. end while
13. end for
14. 得到更新所有样本之后最新的权值和偏置;
15. for all 数据集中每一个样本 do
16. 根据式(1), 式(2)计算隐藏层的输出值;(此步骤, 特征提取并降维)
17. 将降维后的新样本存入文件中保存;
18. end for
1.2 聚类分析本文采用聚类中的系统聚类方法对上述神经网络降维的数据样本进行分类. 对于没有预先处理的水质点位监测数据, 模糊聚类算法是最适合的. 但是由于数据及预先用神经网络进行了降维处理, 特征数量减少, 原本监测点位有限, 因此本文选用了适用于少量特征、少量点位的系统聚类法, 并且运行速度有一定的提升. 首先, 将类别分为n类, 即每个监测点位分为一类, 计算各类之间的距离, 找出所有类间距中的最短距离的两个类, 并合并他们为一个新类, 重新计算
欧式距离公式为:
| $dist(X,Y) = \sqrt {\sum\limits_{i = 1}^n {{{({x_i} - {y_i})}^2}} } $ |
系统聚类算法伪代码如算法2.
算法2. 系统聚类算法
1. 将降维后的数据样本分为
2. for all类别do
3. 计算类间距;
4. 找出类间距中的最短间隔距离;
5. 找到最短间隔的两个类, 合并他们;
6. 合并之后新的类别数目为
7. if (
8. break;
9. end for
2 实验分析本文数据集来源为某市实时监测的各个断面的水质污染物浓度值.
2.1 数据预处理首先对数据进行预处理, 将数据映射到
| ${x_{\rm norm}} = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}}$ |
其中,
实验过程如图1所示, 将标准化、归一化处理后的数据输入自编码器神经网络, 初始化各层之间的权重参数, 初始化隐藏层和输出层的偏置参数, 开始训练. 将自编码器神经网络降维后的新数据样本聚类分析, 产生点位优化的结果.
2.3 评价指标本文首先检验原点位与优化后的点位之前的相关性, 在给定
| 表 1 相关性检验 |
为进一步验证, 本文采用F检验法—方差齐性检验和t检验法验证原点位与优化后的点位之间所监测的数据是否具有一致性. 结果如表2. 所采用的公式为:
| $ \left\{ \begin{split} &{S}_{{\text{合}}}=\sqrt{\frac{\left({n}_{1}-1\right){S}_{1}^{2}+\left({n}_{2}-1\right){S}_{2}^{2}}{{n}_{1}+{n}_{2}-2}}\\ &t=\frac{{\overline{x}}_{1}-{\overline{x}}_{2}}{{S}_{{\text{合}}}}\cdot \frac{n}{2} \end{split}\right.$ |
| 表 2 一致性检验 |
为了进一步验证优化后的点位选择更加精准, 本文通过姚式指数公式同时计算优化后与优化前的水质量指数和原点位的水质量指数进行比较. 结果如表3,公式如下:
| $I = \sqrt {\max \frac{{{C_j}}}{{{S_j}}} \cdot \left[ {\frac{1}{m}\sum\limits_{j = 1}^m {\frac{{{C_j}}}{{{S_j}}}} } \right]} $ |
| 表 3 质量指数对比 |
2.4 结果分析
根据神经网络降维结合聚类所产生的点位选择结果如图3.
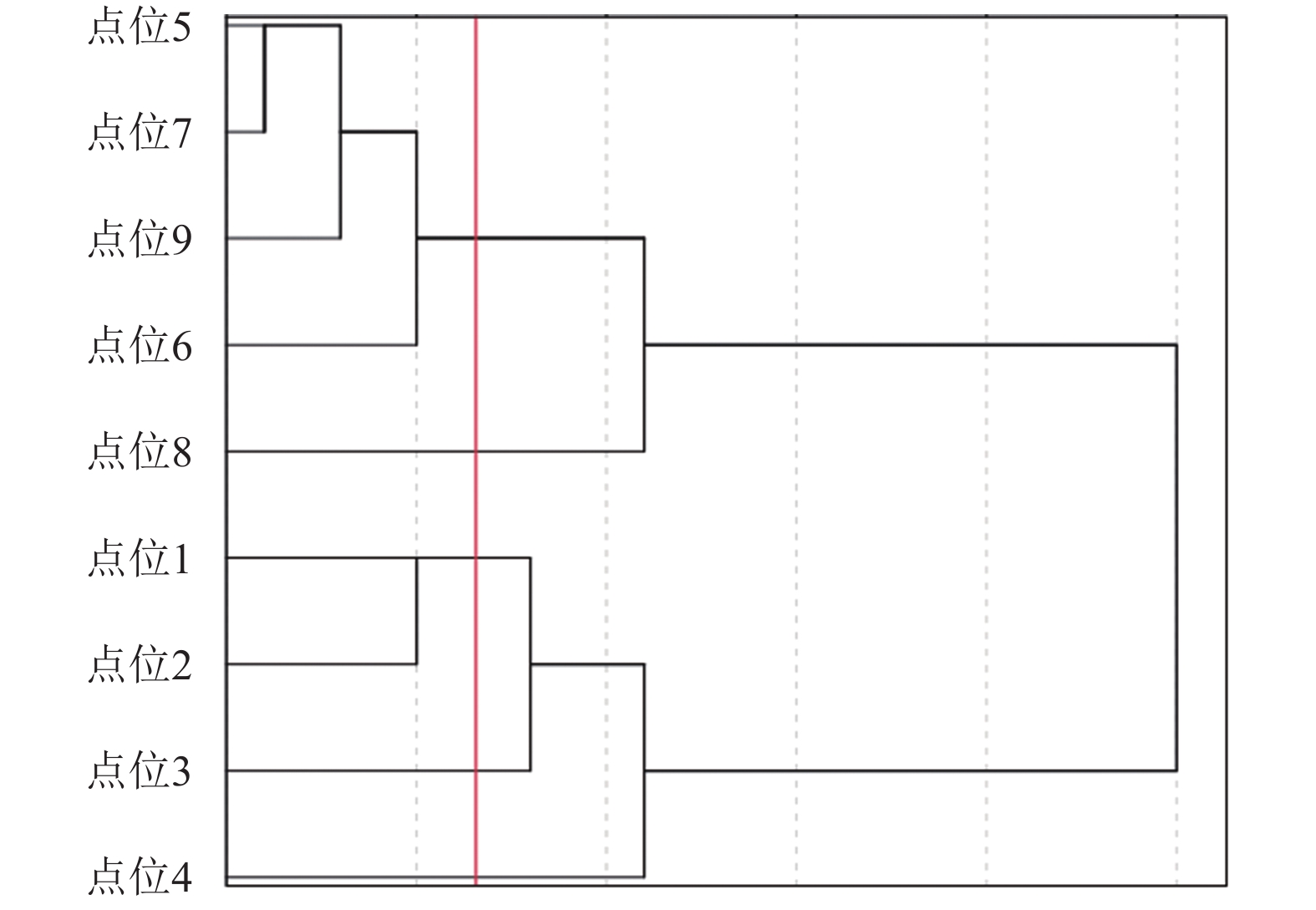
|
图 3 实验结果图 |
如图3所示, 神经网络降维结合聚类的算法选出了从9个监测点位中选出了5个监测点位. 而原本单独使用的模糊聚类算法选出的是6个监测点位. 根据表1所示的相关性检验, 表明原点位与优化后的各污染物浓度密切相关, 无明显差异性. 根据表2结果, 进一步证实了原点位和优化后点位各污染物这两组数据评价结果一致, 表明优化后的点位可以替代原点位. 根据表3结果, 表明本文所选的点位优化算法所产生的5个点位的质量指数, 比模糊聚类算法产生的6个点位更接近原本的9个点位的质量指数. 综上所述, 本文所选算法所产生的点位更能代表全部的9个监测点位.
3 结论本文针对水质点位优化提出了一种神经网络结合聚类的点位优化算法, 通过神经网络对数据进行降维处理, 并通过系统聚类的方法选出合适的点位. 本文所提出的方法相较于单一的聚类方法, 减少了点位的选择, 并且提高了点位选择的准确性, 实现了以尽量少的点位, 保证数据的代表性.
| [1] |
王陆平. 大气质量评价模型和监测点位优化研究[硕士学位论文]. 西安: 西安科技大学, 2017.
|
| [2] |
赵晓亮, 齐庆杰, 赵东洋, 等. 阜新市空气监测点位优化的聚类分析. 地球与环境, 2015, 43(3): 350-355. |
| [3] |
杨剑锋, 乔佩蕊, 李永梅, 等. 机器学习分类问题及算法研究综述. 统计与决策, 2019, 35(6): 36-40. |
| [4] |
徐学良. 人工神经网络的发展及现状. 微电子学, 2017, 47(2): 239-242. |
| [5] |
董鑫, 夏文瀚, 倪健, 等. 受限玻尔兹曼机结合聚类的特异点挖掘方法. 软件导刊, 2020, 19(2): 136-139. |
| [6] |
张春霞, 姬楠楠, 王冠伟. 受限波尔兹曼机. 工程数学学报, 2015, 32(2): 159-173. |
| [7] |
Premachandran V, Yuille AL. Unsupervised learning using generative adversarial training and clustering. Proceedings of 5th International Conference on Learning Representations. Toulon, France. 2017. 1–10.
|
| [8] |
李通, 王红军, 邓萍. 基于聚类的无监督神经网络模型. 2018中国自动化大会(CAC2018)论文集. 西安, 中国. 2018. 650–658.
|
| [9] |
崔广新, 李殿奎. 基于自编码算法的深度学习综述. 计算机系统应用, 2018, 27(9): 47-51. DOI:10.15888/j.cnki.csa.006542 |
| [10] |
Santos EC. Clustering-based resource allocation mechanism in long term evolution advanced networks with auto-encoder for feature learning. Transactions on Emerging Telecommunications Technologies, 2019, 30(7): e3591. |
| [11] |
Zhang ZH, Chen DD, Wang ZL, et al. Depth-based subgraph convolutional auto-encoder for network representation learning. Pattern Recognition, 2019, 90: 363-376. DOI:10.1016/j.patcog.2019.01.045 |
| [12] |
王雅思, 姚鸿勋, 孙晓帅, 等. 深度学习中的自编码器的表达能力研究. 计算机科学, 2015, 42(9): 56-60, 65. |
| [13] |
袁非牛, 章琳, 史劲亭, 等. 自编码神经网络理论及应用综述. 计算机学报, 2019, 42(1): 203-230. |
| [14] |
殷瑞刚, 魏帅, 李晗, 等. 深度学习中的无监督学习方法综述. 计算机系统应用, 2016, 25(8): 1-7. DOI:10.15888/j.cnki.csa.005283 |
| [15] |
邢蕾, 赵鹏飞. BP神经网络的一个解析算例. 科技创新导报, 2016, 13(25): 90-91, 93. |
| [16] |
陈海鹏, 申铉京, 龙建武, 等. 自动确定聚类个数的模糊聚类算法. 电子学报, 2017, 45(3): 687-694. |
 2021, Vol. 30
2021, Vol. 30



