2. 福建省船舶与海洋重点实验室, 厦门 361021
2. Fujian Province Key Laboratory of Naval Architecture and Marine Engineering, Xiamen 361021, China
非线性科学是近些年来研究的热点之一, Wang等[1]将非线性系统应用于伺服电机的控制中, Zhang等[2]应用超谐波响应分析法测试旋转叶片受气压影响的形变程度, Zheng等[3]运用非线性系统到分子动力学, 充分说明了对非线性系统研究的重要性. 自1963年Lorenz提出了第一个具有非线性动力学特性的混沌吸引子, 即Lorenz系统. 此后, 学术界对混沌系统的研究逐渐深入. 2020年, Peng等将改进的返回结果映射法应用于混沌系统的参数估计, 与经典返回结果映射法相比节省了大量的运算时间[4]. Zhuang等[5]应用Jaya-Powell算法估计Lorenz混沌系统的参数, 为边缘计算提供了便利. 国外研究员用改进的粒子群算法估计基于混沌响应的永磁同步电动机模型参数, 并取得了良好的效果[6].
混沌是非线性系统中普遍存在的一种现象, 它作为非线性动力系统的固有特性引起了极大的关注[7], 尤其是混沌系统在生物医学、保密通信以及信息科学等领域需求的推动下, 致使许多国内外研究者加入研究, 并提出了大量的研究方法[8-10], 但这些研究方法大多以参数已知为前提. 在许多实际应用中, 由于系统的复杂性等因素, 导致系统参数在大多数情况下是无法确定的, 为了降低在参数寻优过程中的难度, 需要对未知参数设置一定的范围, 所以对混沌系统中的未知参数进行有效评估成为混沌系统中的关键问题[11]. 对混沌系统中的未知参数进行有效评估实质是多维复杂函数优化问题, 群体智能优化算法对解决复杂函数优化问题提出了有效的方案. 例如: 人工蜂群算法[12]、萤火虫算法[13]、差分进化算法[14]、花朵授粉算法[15]、粒子群算法[16]等相继被用于对混沌系统的参数估计, 具有比传统优化算法更好的效果.
人工蜂群算法是仿生智能计算领域中一种十分典型的群体智能优化算法, 它是通过模仿蜜蜂的采蜜过程而得到的, 主要特点是可以直接通过对局部候选解的优劣进行比较, 选出全局最优值[17]. 相比其他群智能优化算法, 人工蜂群算法在处理多维问题及全局搜索方面所需参数较少, 计算简单,易于实现等优点[18,19]. 故本文利用人工蜂群算法解决混沌系统中参数估计的问题.
1 混沌系统参数估计定义m个参数的n维混沌系统的状态变量估计值如式(1):
| $\dot X = F(X,{X_0},\theta )$ | (1) |
式(1)中,
假设系统结构已知, 当对系统参数进行估计时被估计系统可定义为式(2):
| $\dot Y = F\left( {Y,{X_0},\hat \theta } \right)$ | (2) |
式(2)中,
参数估计问题也可转化为式(3):
| $\hat \theta = \arg \mathop {\min }\limits_\theta J(\theta ) = \arg \mathop {\min }\limits_\theta \frac{1}{N}\sum\limits_{i = 1}^N {||{x_i}} - {y_i}|{|^2}$ | (3) |
式(3)中, N表示用于状态变量的数据长度, xi和yi分别表示在其状态变量下系统的真值和估计值. 显然,
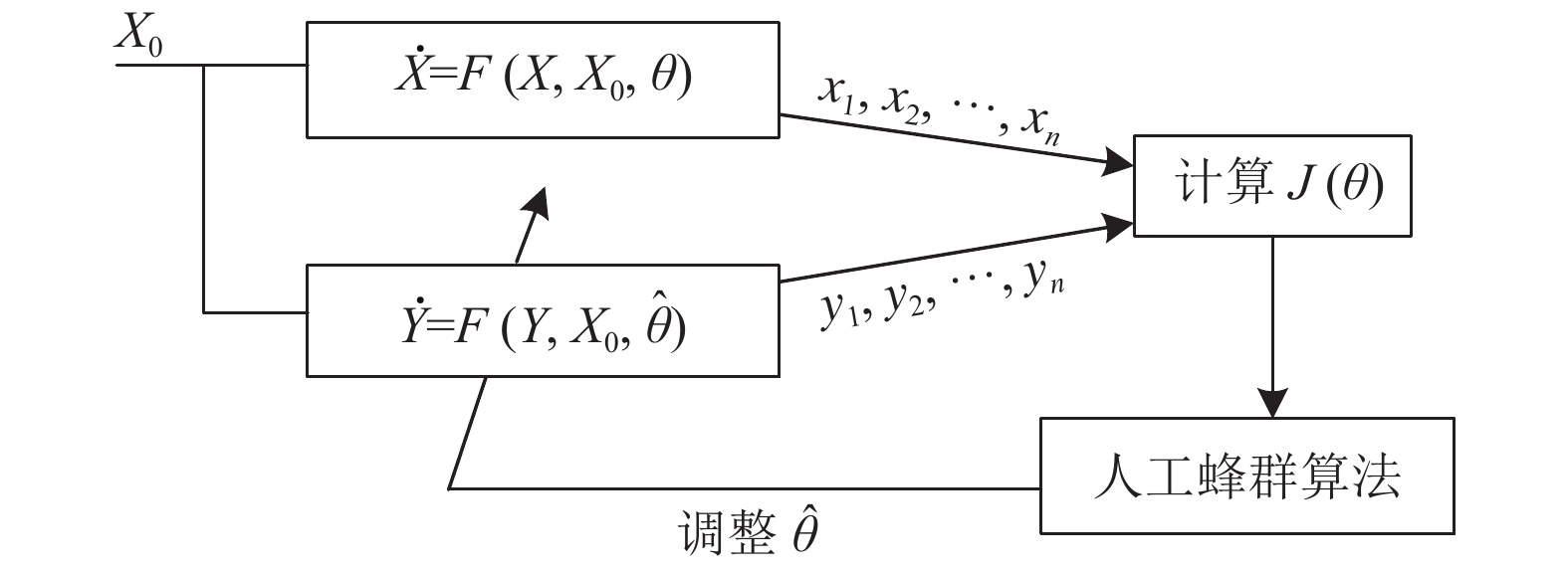
|
图 1 混沌系统参数估计框图 |
2 基于人工蜂群算法的混沌系统参数估计 2.1 人工蜂群算法
人工蜂群算法(Artificial Bee Colony algorithm, ABC)是一种通过模仿蜜蜂的采蜜过程而得到的优化算法, 它是由土耳其学者Karaboga于2005年提出的用来解决多变量函数的优化问题[20]. 通过对问题的局部寻优行为, 找到全局最优值的过程. ABC算法主要有初始化、雇佣蜂、观察蜂和侦查蜂4个阶段.
初始化阶段: ABC算法在初始化阶段, 每只雇佣蜂会随机产生一个食物源, 每个食物源与待优化解的个数
| $V(i,j) = {V_{\min }}(j) + {{rand}} \times {\rm{[}}{V_{\max }}(j) - {V_{\min }}(j){\rm{]}}$ | (4) |
式(4)中,
雇佣蜂阶段: 在此阶段, 每只雇佣蜂通过搜索方程在其当前位置的附近生成新的食物源VEB(i), 其搜索方程如式(5):
| ${V_{{\rm{EB}}}}(i,j) = V(i,j) + \lambda \times [V(i,j) - V(r,j)]$ | (5) |
式(5)中,
当得到新的食物源VEB(i), 便对其进行评估且与旧的食物源V(i)进行比较. 如果VEB(i)的适用性优于V(i), 则将VEB(i)替换V(i); 否则保留V(i).
观察蜂阶段: 当所有雇佣蜂搜索完成后, 它们通过舞蹈分享保存的信息给观察蜂. 观察蜂根据相应的概率在雇佣蜂传递的信息基础上更新候选解, 并评估其适应度选择食物源. 更新方程如式(6):
| ${V_{{\rm{OB}}}}(i,j) = V(i,j) + \beta \times [V(i,j) - V(k,j)]$ | (6) |
式(6)中,
当得到新的食物源VOB(i), 便对其进行评估且与更新的食物源V(i)进行比较. 如果VOB(i)的适用性优于V(i), 则将VOB(i)替换V(i); 否则保留V(i).
侦查蜂阶段: 为了防止陷入局部最优, 对于连续klimit次没更新的解由式(4)重新生成新的候选解代替它.
当得到新的候选解VSB(i), 便对其进行评估且与原候选解V(i)进行比较. 如果新候选解的适用性优于原候选解, 则替换它; 否则保留原候选解.
ABC算法的优化流程图如图2所示.
2.2 基于人工蜂群算法的混沌系统参数估计法的实现虽然ABC算法在处理多维问题及全局搜索方面所需参数较少, 计算简单, 易于实现. 但其收敛速度相对较慢, 精度不高.
本节为充分利用搜索方程对蜂源进行搜索得到优化解, 引入了可选择的概率p得到新的搜索机制, 舍弃了概率计算和限制次数内蜂群没替换重新生成随机蜂群的方法, 算法的具体改进之处如下.
在雇佣蜂阶段, 改用搜索方程如式(7):
| ${V_{{\rm{EB}}}}(i,j) = {V_{\min }}(j) + {V_{\max }}(j) - V(i,j)$ | (7) |
式(7)中,
在观察蜂阶段, 引用了差分进化中变异[21]的方法. 其搜索方程如式(8):
| ${V_{{\rm{OB}}}}(i,j) = {V_{{\rm{best}}}}(j) + \phi \times [V({r_1},j) - V({r_2},j)]$ | (8) |
式(8)中,
在侦查蜂阶段, 引用了概率p, 如果
| ${V_{{\rm{SB}}}}(i,j) = V(i,j) + \phi \times [V(i,j) - V(k,j)]$ | (9) |
式(9)中,

|
图 2 ABC算法流程图 |
本文ABC算法的优化步骤如算法1所示.
算法1. 本文ABC算法
1.初始化阶段: 设置最大迭代次数FEmax, 蜜蜂个数为
While (符合终止条件)
2. 雇佣蜂阶段:
由式(7)更新参数估计值, 并通过式(3)计算得到目标函数值J2;
将当前最优目标函数值J1和J2进行比较, 最小值即为最优值, 选出最优值放于J1.
3. 观察蜂阶段:
由式(8)更新参数估计值, 并通过式(3)计算得到目标函数值J3;
将当前最优目标函数值J1和J3进行比较, 最小值即为最优值, 选出最优值放于J1.
4. 侦察蜂阶段:
比较概率p和rand的大小, 根据比较结果决定是否更新参数估计值;
由式(9)更新参数估计值, 并通过式(3)计算得到目标函数值J4;
将当前最优目标函数值J1和J4进行比较, 最小值即为最优值, 选出最优值放于J1.
迭代次数
End
3 仿真分析 3.1 基准函数测试为了验证本文ABC算法的有效性, 将本文ABC算法和ABC算法及文献[12]中的IABC算法的优化能力进行评估. 分别采用了Sphere函数、Griewank函数、Ragstrigin函数、Rosenbrock函数、Ackley函数、Schaffer函数6个标准的测试函数进行测试, 测试函数的表达式、维度、搜索范围及函数最优值如表1所示[22].
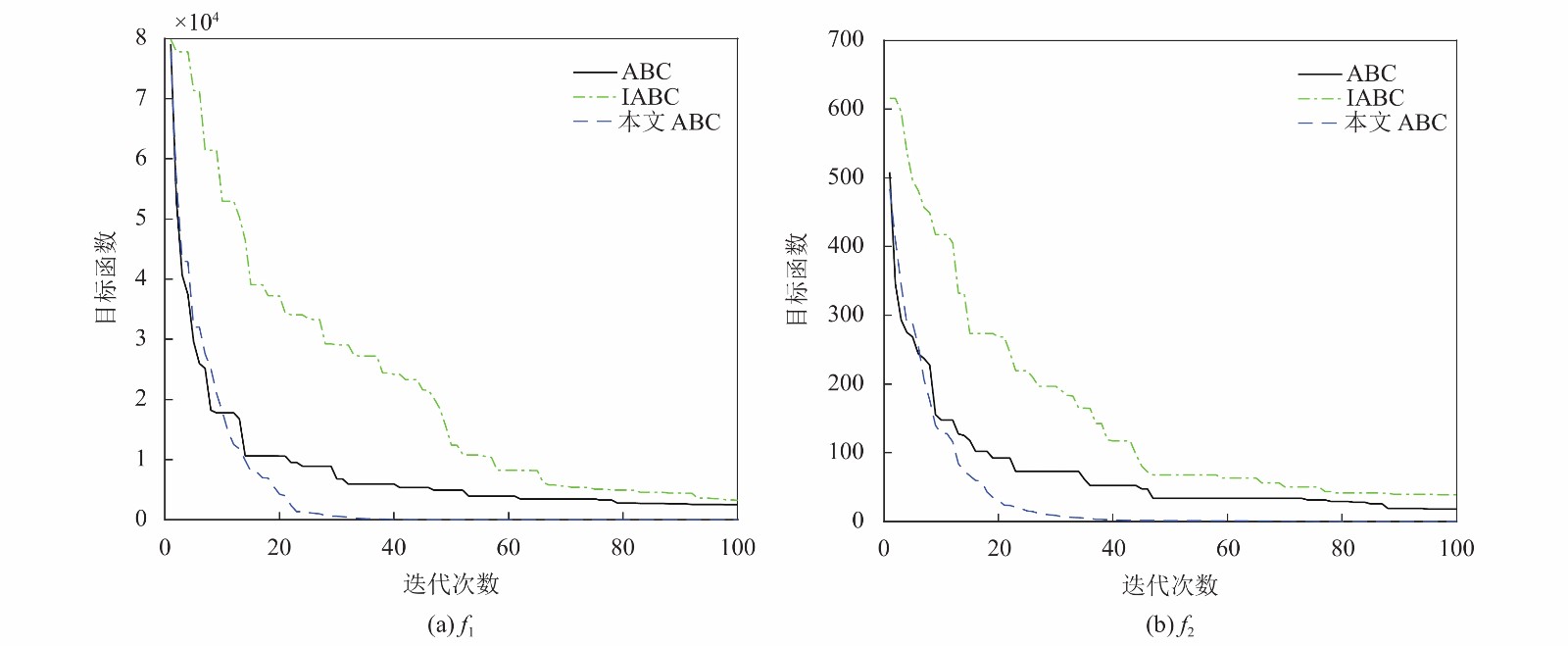
将所有函数的最大迭代次数FEmax设置为100, 各函数的收敛曲线如图3所示. 从各函数的收敛曲线图可以看出, 本文ABC算法与ABC算法及IABC算法相比下降趋势更快、坡度更陡、所用迭代次数更少, 其函数f3、f5和f6尤为明显. 故本文ABC算法相比ABC算法和IABC算法收敛速度更快, 优化效果更佳. 这说明本文ABC算法是可行的.
| 表 1 标准测试函数 |
|

|
图 3 标准测试函数收敛曲线 |
3.2 Lorenz系统参数估计
Lorenz系统是最典型的混沌系统[23,24], 这里以Lorenz系统为例, 验证本文ABC算法对混沌系统中未知参数估计的适用性. Lorenz系统的状态方程如式(10):
| $\left\{ \begin{array}{l} \dot x = a(y - x) \\ \dot y = bx - y - x{\textit{z}} \\ \dot {\textit{z}} = xy - c{\textit{z}} \\ \end{array} \right.$ | (10) |
式(10)中
未知参数的真实值a=10, b=28, c=8/3. 以x(0)=0.1, y(0)=0.1, z(0)=0为初始状态值对系统进行仿真, 设置采样次数N=10000. 数值仿真采用四阶Rayleigh-Benard法[25]来计算式(10)中每个整数点的变量值, 步长h=0.01, 混沌系统[26]如图4所示.

|
图 4 Lorenz混沌吸引子三维图 |
在本文ABC算法中, 设置最大迭代次数FEmax=100, 种群大小SN=20, 混沌系统的未知参数范围设置为:
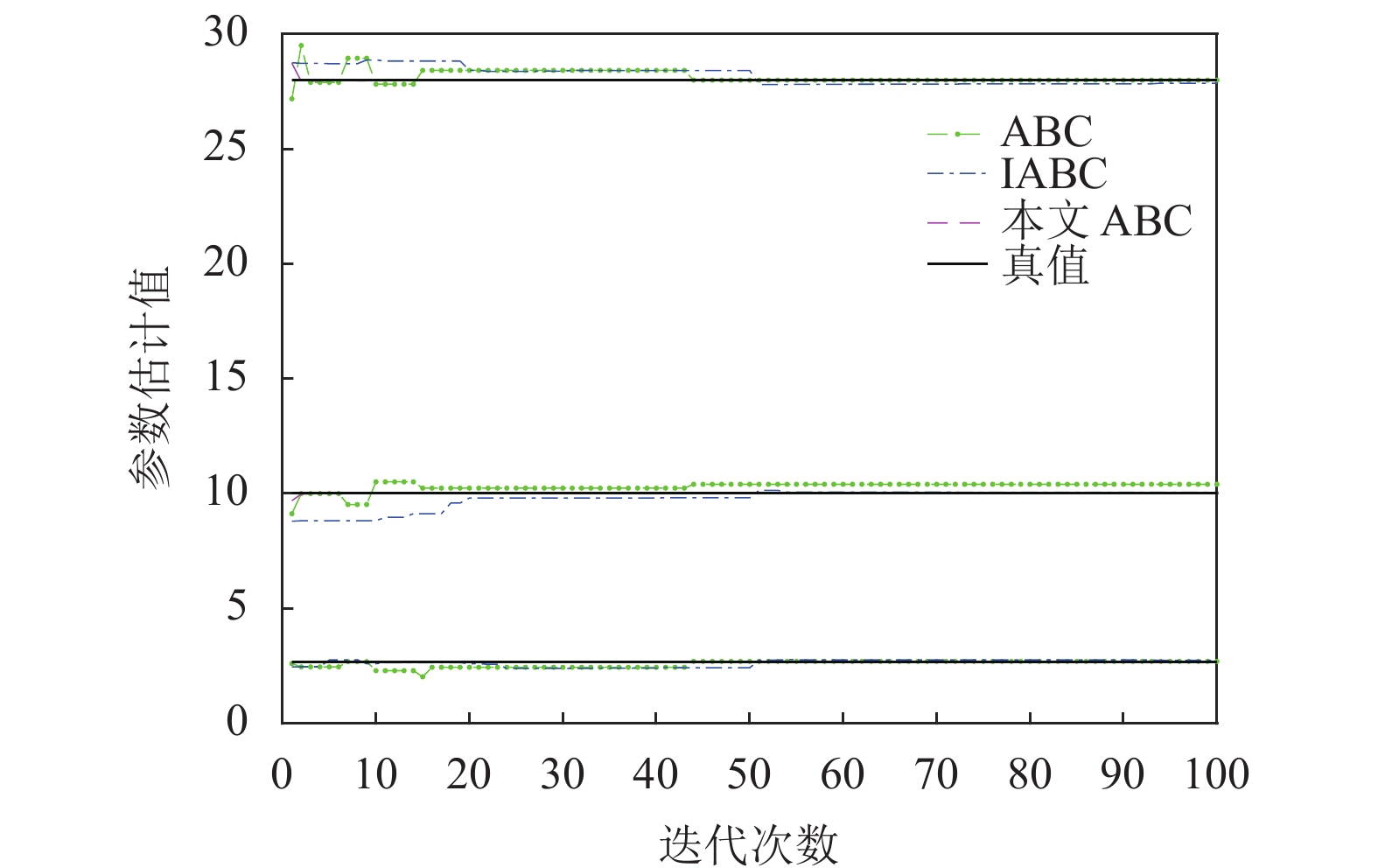
|
图 5 参数估计值收敛曲线 |

|
图 6 目标函数值收敛曲线 |
由图5和图6仿真结果可以得出, 本文ABC算法的收敛性及稳定性明显优于ABC算法及IABC算法.图7、图8和图9分别是通过两种算法得到的最优估计参数值由式(10)得出的状态变量估计值和真值之间的对比图, 其中误差e(t)的方程如式(11).
| $e(t) = \sum\limits_{t = 0}^{N - 1} {\left| {{\delta _i}(t) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta } (t)} \right|} $ | (11) |
式(11)中
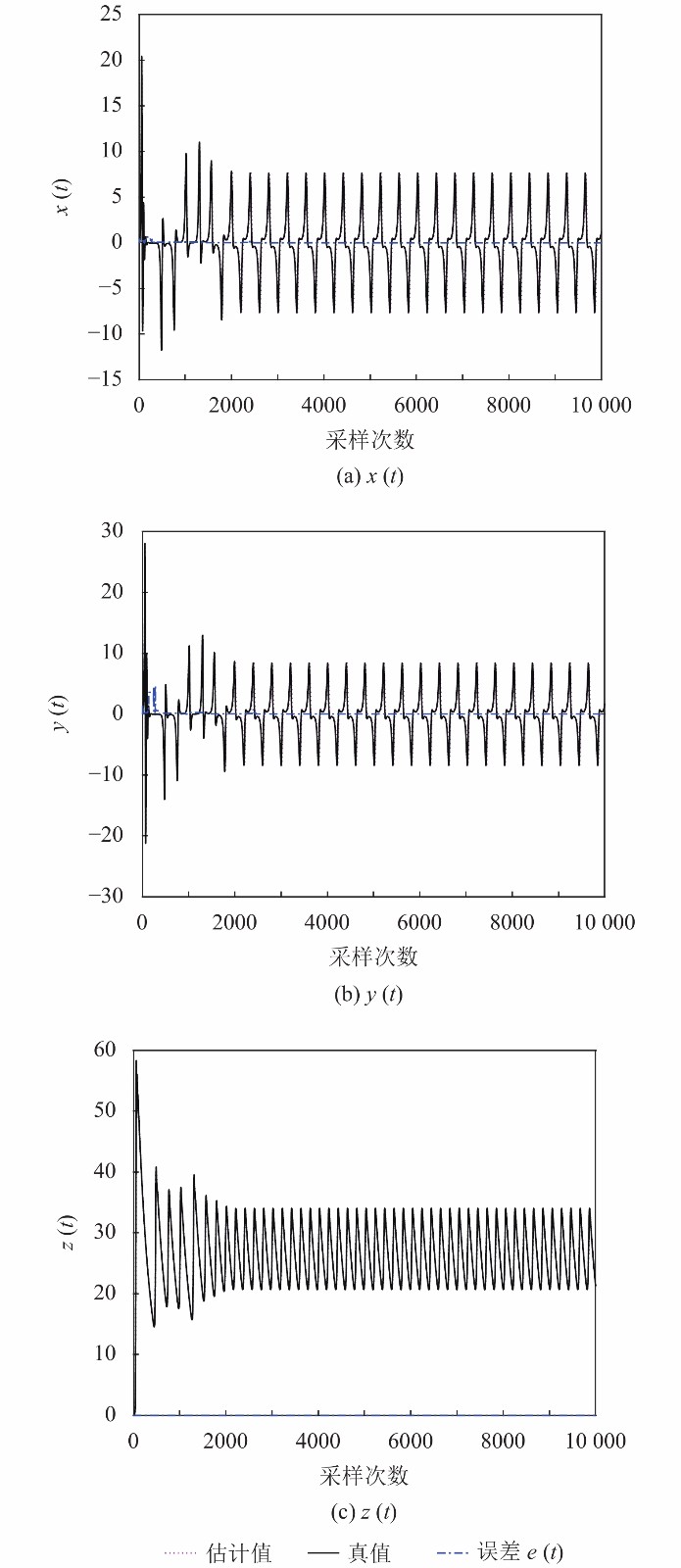
|
图 7 ABC算法状态变量 |
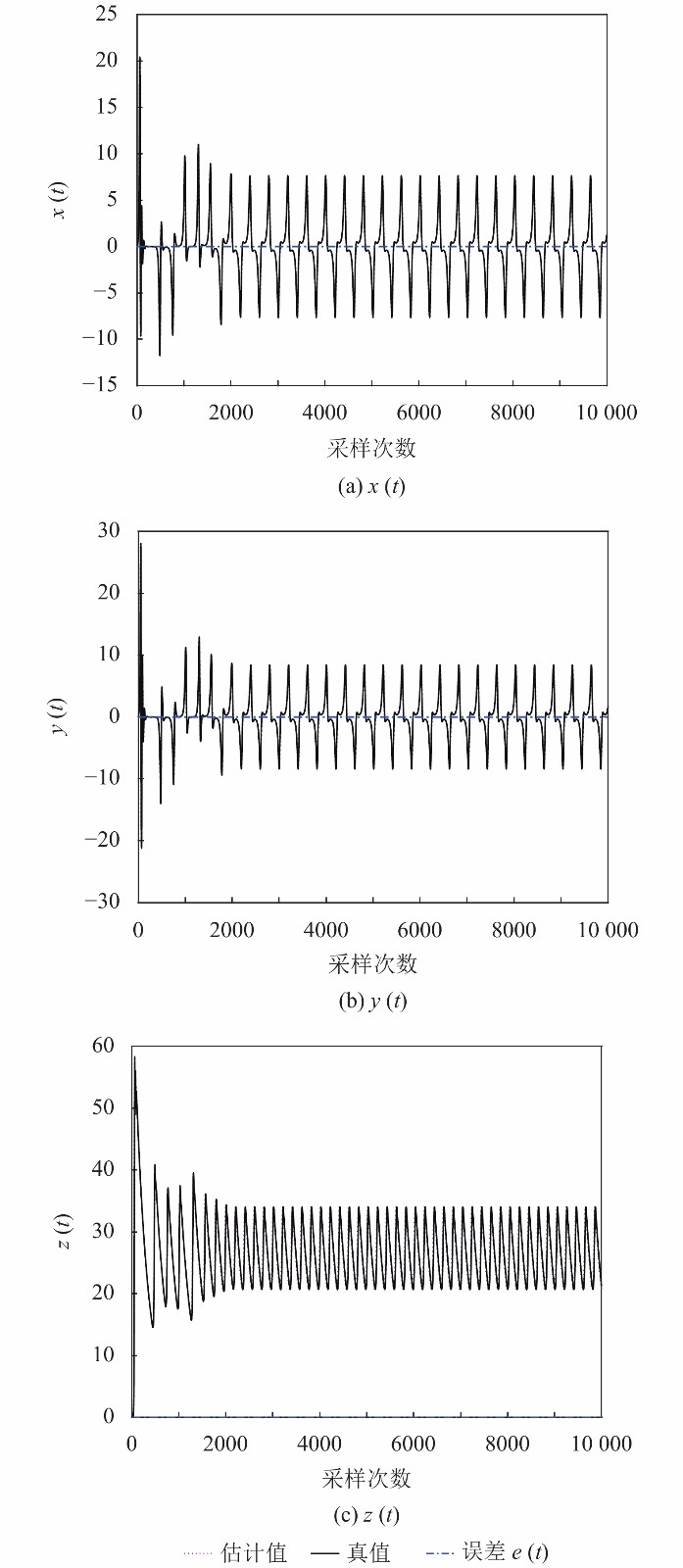
由图7~图9可见, 图9中真值和估计值曲线更趋近于重合尤其随采样次数的增大, 重合度越高, 而图7中的真值和估计值曲线在随采样次数增大时有明显的分叉现象, 图8的重合度相比于图9较差, 所以本文ABC算法的趋近性明显优于ABC算法和IABC算法. 参数a、b、c及目标函数的最优值、最差值和平均值是由ABC算法和本文ABC算法及IABC算法分别独立运行30次计算得到的平均值, 记录于表2.

|
图 8 IABC算法状态变量 |
由表2可以得出, 在最优值、最差值和平均值上由本文ABC算法仿真得出的参数a趋近于10、参数b趋近于28、参数c趋近于8/3的效果明显优于由ABC算法和IABC算法仿真得出的参数趋近值. 利用本文ABC算法得出的目标函数值也明显小于由ABC算法和IABC算法得出的目标函数值, 故本文ABC算法在稳定性及收敛速度上明显优于ABC算法和IABC算法.
|
图 9 本文ABC算法状态变量 |
| 表 2 文献[14]ABC和本文ABC算法参数估计结果 |
4 结论
针对人工蜂群算法收敛速度相对较慢, 精度不高,本文首先引入了可选择的概率p得到新的搜索机制; 在此基础上, 将混沌系统中复杂的参数估计问题转化为多维问题, 利用改进的人工蜂群优化算法求解混沌系统的参数. 测试函数优化实验证了人工蜂群算法改进方案的有效性; Lorenz混沌系统的参数辨识仿真实验结果表明了本文的基于人工蜂群算法的混沌系统参数辨识方法比传统ABC算法及IABC算法具有更高的估计精度, 且较快的收敛速度.
| [1] |
Wang SB, Na J. Parameter estimation and adaptive control for servo mechanisms with friction compensation. IEEE Transactions on Industrial Informatics, 2020, 16(11): 6816-6825. DOI:10.1109/TII.2020.2971056 |
| [2] |
Zhang B, Ding H, Chen LQ. Super-harmonic resonances of a rotating pre-deformed blade subjected to gas pressure. Nonlinear Dynamics, 2019, 98(4): 2531-2549. DOI:10.1007/s11071-019-05367-x |
| [3] |
Zheng HW, Wang RB, Qiao LK, et al. The molecular dynamics of neural metabolism during the action potential. Science China Technological Sciences, 2014, 57(5): 857-863. DOI:10.1007/s11431-014-5530-4 |
| [4] |
Peng YX, Sun KH, He SB. An improved return maps method for parameter estimation of chaotic systems. International Journal of Bifurcation and Chaos, 2020, 30(4): 2050058. DOI:10.1142/S0218127420500583 |
| [5] |
Zhuang L, Cao LP, Wu Y, et al. Parameter estimation of Lorenz chaotic system based on a hybrid Jaya-Powell algorithm. IEEE Access, 2020, 8: 20514-20522. DOI:10.1109/ACCESS.2020.2968106 |
| [6] |
Yousri D, Allam D, Eteiba MB, et al. Chaotic heterogeneous comprehensive learning particle swarm optimizer variants for permanent magnet synchronous motor models parameters estimation. Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 2020, 44(3): 1299-1318. DOI:10.1007/s40998-019-00294-4 |
| [7] |
Lazzús JA, Rivera M, López-caraballo CH. Parameter estimation of Lorenz chaotic system using a hybrid swarm intelligence algorithm. Physics Letters A, 2016, 380(11–12): 1164-1171. |
| [8] |
Kapitaniak T, Mohammadi SA, Mekhilef S, et al. A new chaotic system with stable equilibrium: Entropy analysis, parameter estimation, and circuit design. Entropy, 2018, 20(9): 670. DOI:10.3390/e20090670 |
| [9] |
Shekofteh Y, Jafari S, Rajagopal K. Cost function based on hidden Markov models for parameter estimation of chaotic systems. Soft Computing, 2019, 23(13): 4765-4776. DOI:10.1007/s00500-018-3129-6 |
| [10] |
石建平, 李培生, 刘国平, 等. 基于改进粒子群优化算法的混沌系统参数估计. 华中科技大学学报(自然科学版), 2018, 46(9): 70-76. |
| [11] |
Peng YX, Sun KH, He SB, et al. Parameter estimation of a complex chaotic system with unknown initial values. The European Physical Journal Plus, 2018, 133(8): 305. DOI:10.1140/epjp/i2018-12091-1 |
| [12] |
Ding ZH, Lu ZR, Liu JK. Parameters identification of chaotic systems based on artificial bee colony algorithm combined with cuckoo search strategy. Science China Technological Sciences, 2018, 61(3): 417-426. DOI:10.1007/s11431-016-9026-4 |
| [13] |
Mousavi Y, Alfi A. Fractional calculus-based firefly algorithm applied to parameter estimation of chaotic systems. Chaos, Solitons & Fractals, 2018, 114: 202-215. |
| [14] |
Liu FC, Li X, Liu X, et al. Parameter identification of fractional-order chaotic system with time delay via multi-selection differential evolution. Systems Science & Control Engineering, 2017, 5(1): 42-48. |
| [15] |
Xu SH, Wang Y, Liu X. Parameter estimation for chaotic systems via a hybrid flower pollination algorithm. Neural Computing and Applications, 2018, 30(8): 2607-2623. DOI:10.1007/s00521-017-2890-2 |
| [16] |
Huang Y, Guo F, Li YL, et al. Parameter estimation of fractional-order chaotic systems by using quantum parallel particle swarm optimization algorithm. PLoS One, 2015, 10(1): e0114910. DOI:10.1371/journal.pone.0114910 |
| [17] |
Zhang P, Yang RY, Yang RH, et al. Parameter estimation for fractional-order chaotic systems by improved bird swarm optimization algorithm. International Journal of Modern Physics C, 2019, 30(11): 1950086. DOI:10.1142/S0129183119500864 |
| [18] |
Biswas S, Chatterjee A, Goswami SK. An artificial bee colony-least square algorithm for solving harmonic estimation problems. Applied Soft Computing, 2013, 13(5): 2343-2355. DOI:10.1016/j.asoc.2012.12.006 |
| [19] |
Zhang M, Tan YT, Zhu JH, et al. Modeling and simulation of improved artificial bee colony algorithm with data-driven optimization. Simulation Modelling Practice and Theory, 2019, 93: 305-321. DOI:10.1016/j.simpat.2018.06.004 |
| [20] |
Karaboga D, Basturk B. A powerful and efficient algorithm for numerical function optimization: Artificial Bee Colony (ABC) algorithm. Journal of Global Optimization, 2007, 39(3): 459-471. DOI:10.1007/s10898-007-9149-x |
| [21] |
Yildizdan G, Baykan ÖK. A novel modified bat algorithm hybridizing by differential evolution algorithm. Expert Systems with Applications, 2020, 141: 112949. DOI:10.1016/j.eswa.2019.112949 |
| [22] |
Peng YX, Sun KH, He SB, et al. The influence of samples on meta-heuristic algorithm for parameter estimation of chaotic system. Modern Physics Letters B, 2019, 33(4): 1950041. DOI:10.1142/S0217984919500416 |
| [23] |
Shams Z, Shahmansoorian A. Fault estimation based on observer for chaotic lorenz system with bifurcation problem. Transactions of the Institute of Measurement and Control, 2020, 42(3): 576-585. DOI:10.1177/0142331219879267 |
| [24] |
石建平, 李培生, 刘国平. 基于混合群智能优化算法的混沌系统参数估计. 计算物理, 2019, 36(5): 621-630. |
| [25] |
Cornick M, Hunt B, Ott E, et al. State and parameter estimation of spatiotemporally chaotic systems illustrated by an application to Rayleigh-Bénard convection. Chaos, 2009, 19(1): 013108. DOI:10.1063/1.3072780 |
| [26] |
Chen Y, Pi DC, Wang B. Enhanced global flower pollination algorithm for parameter identification of chaotic and hyper-chaotic system. Nonlinear Dynamics, 2019, 97(2): 1343-1358. DOI:10.1007/s11071-019-05052-z |
 2021, Vol. 30
2021, Vol. 30



