滚动轴承作为许多机械的基础零部件, 其运行状态往往会影响整台机械的工作状态, 对生产和安全造成直接影响[1]. 有关资料记载, 大型企业因滚动轴承故障而引发的一次生产线非计划停产造成的经济损失可达数千万元[2]. 因此对滚动轴承进行科学有效的故障诊断具有十分重要的意义.
故障诊断方法的研究主要分为基于解析模型和基于数据驱动两方面. Hsiao等[3]提出了一种分层多模型方案来检测和隔离机器人机械手的执行器故障. 代祥[4]提出了一种电网信息物理模型故障诊断优化模型, 将故障问题表示成求解目标函数是极值的0-1整数规划问题, 从而通过严密的数学方法来确定故障元件. 基于解析模型的方法需要对故障诊断问题进行解析化表达, 对于复杂度较高的系统建模难度大, 且建立的模型在其他系统上的普适性较低[4], 实际推广使用具有一定局限性. 近年来, 随着机器学习研究的兴起, 基于数据驱动的故障诊断方法已成为重点研究领域之一[5]. 姚德臣等[6]将改进后的支持向量机(SVM)应用于轴承的故障诊断研究当中. Peng等[7]将主成分分析(PCA)算法应用到电动潜水器泵轴的损坏原因检测中. Yang等[8]将BP人工神经网络(BPNN)应用于滚动轴承的故障诊断. 这些传统的基于数据驱动的方法都取得了相对不错的效果, 但随着人工智能技术的发展, 现已证实这些浅层网络结构, 因其特征提取能力不足, 难以挖掘提取故障数据中更深层次的微小特征[9], 从而限制了诊断准确率的提升.
随着互联网、物联网等快速兴起与普及, 当前社会数据的增长速度比以往任何时期都要迅猛[10]. 大数据给深度神经网络提供了充足的训练“原料”, 给基于数据驱动的机械智能故障诊断的深入研究和应用提供了新的机遇[11].
深度学习理论由Hinton等[12]于2006年提出, 近年来, 深度学习技术因其强大的特征提取和学习能力在语音识别[13]和计算机视觉[14]领域迅速发展, 并产生了许多新的突破. 卷积神经网络(CNN)由LeCun等[15]于1989年提出. 2012年, Krizhevsky等[14]将卷积神经网络与深度学习理论结合提出“AlexNet”网络结构. 深度卷积网络能够由浅到深逐步抽象特征, 自动特征提取, 其独特的网络结构能有效的在保留数据特征的同时减少参数数量降低数据复杂度, 并通过多层次的非线性映射关系学习深层次的故障特征[16]. 将深度学习技术应用于故障诊断领域产生了不错的效果, 宫文峰等[17]通过引入全局均值池化技术代替传统CNN的全连接层部分, 使用改进后的CNN算法识别轴承故障种类. 杜小磊等[18]提出一种基于SSST和DCCNN的滚动轴承故障诊断方法提高了信号的时频分辨率.
上述研究都只是单独使用深度CNN进行训练, 忽略了滚动轴承在发生故障时的时序特征. 滚动轴承性能退化是依存于服役时间的连续演化过程, 相较于常规“事后诊断”, 变工况下滚动轴轻微损伤甚至早期退化状态的准确识别对于指导预测性维护工作等有更大价值[19].
CNN有着强大的图像特征提取能力, 但在处理带时序问题时准确率和效率都没有循环神经网络(RNN)高, RNN可以学习到历史信息, 因而RNN更适合处理时间序列. 作为RNN的变体, 长短期记忆网络(LSTM)通过遗忘门、输入门和输出门等机制解决了普通RNN不易处理的远距离信息上下文依赖、梯度消失或梯度爆炸等问题. LSTM在语音识别、文本识别等方面有成功的应用, 同时也被用于故障诊断领域提取故障信号时间序列的特征. Qu等[20]使用基于LSTM的深度学习方法对研磨系统进行故障诊断, 诊断错误率小于3%. 于洋等[21]使用LSTM结合迁移学习实现了多种类型工况下轴承故障声发射信号特征的自适应提取与智能识别.
针对以上分析, 本文拟将CNN与LSTM的优势结合, 提出一种首先使用CNN提取数据特征, 再结合LSTM处理时序特征的滚动轴承故障诊断方法. 为了最大程度的保留振动信号的时序特征, 采用一维卷积神经网络(1D-CNN)进行特征提取, 用全局池化层代替传统CNN网络架构中的Flatten层以及全连接层, 从而避免Flatten操作和全连接层带来的参数特征的割裂. 以达到减少人工特征提取时间、适应时序问题、提高故障诊断精度的目的.
1 1D-CNN-LSTM诊断模型 1.1 CNN模型CNN模型通常包含3个主要组成部分: 卷积层、池化层、全连接层. 卷积层的作是通过对输入数据的局部区域与卷积核进行卷积运算, 通过滑动卷积核窗口使局部感受野遍历整个输入数据. 卷积计算公式如下:
| $ x_i^l = f\left( {W_i^l*{X^{(l - 1)}} + b_i^l} \right) $ | (1) |
式中,
池化层的作用是空间合并也叫做子采样或者下采样, 可以在保持最重要信息的同时降低特征图的维度. 它有多种类型, 一般采用平均池化或者最大池化, 采用最大池化表达式为:
| $ y_i^{(l + 1)}(j) = \max x_i^j(k)\;\;k \in {D_j} $ | (2) |
式中,
全连接层是一个传统的多层感知器, 在输出层使用一个Softmax激活函数. 主要作用就是将前面提取到的特征结合在一起进行非线性激活输出各分类的概率分布然后进行分类, 表达式为:
| $ p({y_j}) = \frac{{\exp ({y_j})}}{{\displaystyle\sum\limits_{k = 1}^m {\exp ({y_k})} }} $ | (3) |
式中,
长短期记忆网络(LSTM)[22], 是一种带有记忆功能的神经网络, 是RNN的一种变种, LSTM对时序型数据处理具有极为优秀的表现, 被广泛应用于自然语言处理等领域. LSTM使用输入门、输出门与遗忘门实现对信息的控制. 单个LSTM神经元如图1所示, 图中
遗忘门用于控制先前时刻的状态是否保留到当前神经元状态, 实现对记忆的筛选. 输入门将前一时刻的状态值与当前输入值输入激活函数Sigmoid,得到一个重要度值来决定信息的更新情况, 再通过tanh函数来处理前一时刻的状态值和输入信息得到候选单元状态. 输出门控制单元状态的最终输出, 单元状态通过输出门的过滤, 经由tanh函数压缩得到单元最终输出.

|
图 1 LSTM神经元结构图 |
1.3 改进的1D-CNN-LSTM故障诊断模型
在使用CNN处理一般二维图像信号时通常会选用二维卷积核(2D-CNN), 而滚动轴承性能退化一般是依存于服役时间的连续演化过程, 因此原始的滚动轴承故障振动信号一般为基于时间序列的一维数据. 宫文峰等[18]通过人工裁剪和堆叠将一维振动信号处理成了二维图像进行诊断. 这种处理方法割裂了数据的时间序列连续性, 导致模型难以捕捉振动信号的时间序列特性. 本文模型为了保留输入振动信号的时间序列信息, 以及尽量减少人工处理信息操作, 直接使用一维卷积核对一维的时间序列振动信号进行卷积处理(1D-CNN), 避免了时间序列的割裂.
传统的CNN在卷积层之后同常会使用Flatten层降维再使用全连接层得到目标形状的特征向量进行分类或预测. Flatten操作通过将二维矩阵按行或列展平来实现数据降维, 其在按行或列拆分图形矩阵时改变了各数据的空间位置, 从而丢失了部分有用特征. 本文采用最大池化层代替Flatten层和全连接层作为1D-CNN层与LSTM层之间的连接, 来避免这部分特征的丢失. 这种类似全卷积网络的结构支持网络采用反卷积层对最后一个卷积层的特征图进行上采样, 使它恢复到与输入图像相同的尺寸, 因此通过这种方法输入到下一步即LSTM层中的特征图保留了原始输入的空间信息.
本文提出的基于1D-CNN-LSTM的故障诊断方法网络结构如图2所示, 模型主要分为1D-CNN部分、LSTM部分以及分类输出部分, 损失函数采用交叉熵损失函数, 梯度下降采用Adam优化器. 输入信号为同一工况下滚动轴承不同状态的振动信号. 1D-CNN部分通过一系列的一维卷积层来提取振动信号图像特征, 并通过MaxPooling操作逐渐降低特征图维度. 这一操作降低了输入LSTM部分数据的复杂度, 既可以加快LSTM网络处理信号的速度, 同时又避免了Flatten操作, 尽可能的保留了输入数据的时序特征, 确保了模型的精度. LSTM部分由两层LSTM网络构成, 借由LSTM独特的网络结构, 通过遗忘门、输入门、输出门的选择过滤操作可以进一步提取出1D-CNN部分所忽略的时间序列特征, 从而提高故障诊断模型的精度. 最后通过Softmax层分类输出该振动信号所表示的滚动轴承的工作状态, 模型各层具体参数如表1所示.

|
图 2 模型结构图 |
| 表 1 1D-CNN-LSTM结构参数 |
由于提出的模型具有较深的网络结构, 为了增强模型鲁棒性, 防止发生过拟合现象, 模型在1D-CNN部分与LSTM部分连接处引入了随机丢弃机制(dropout), 随机丢弃神经元之间的权重, 从而降低网络对某一单一神经元的依赖, 该操作同样可以降低输入振动信号中带有的噪声影响, dropout层按一定的比例随机将神经元权重置为0, 其表达式为:
| $ r_i^l \sim Bernoulli(p) $ | (4) |
| $ {\tilde X^l} = {r^l}{X^l} $ | (5) |
式中,
本实验数据来自美国凯斯西储大学(CWRU)的轴承实验平台. 如图3所示, 实验平台包括一个2马力的电机, 一个转矩传感器, 一个功率计以及电子控制设备(没有显示), 被测试轴承支承电机轴. 模拟现实中的点蚀等故障, 实验使用电火花加工技术在轴承上布置了单点故障. 实验中使用加速度采集振动信号, 传感器安放在电机壳体上. 振动数字信号的采样频率为12 kHz, 驱动端轴承故障数据同时以48 kHz的采样频率采集.

|
图 3 轴承振动数据采集试验台 |
外圈故障是固定不变的, 为了对该故障相对于轴承受载区域的位置对电机/轴承系统的振动响应直接影响进行定量研究, 实验中分别对驱动和风扇端的轴承外圈布置3、6以及12点钟方向的故障.
本实验选择了在同一工况下驱动端滚动轴承的6种不同状态的12 kHz采样振动信号数据作为实验数据集, 滚动轴承数据集详细信息如表2所示.
实验选取样本为载荷为1马力, 转速约为1772 r/min的驱动端滚动轴承的6种工作状态数据作为训练数据. 12 kHz采样频率下每秒采集12000个点, 转轴每转一圈传感器采集的点数为406个点(12000×60/1772≈406), 在保障数据可信度的情况下考虑到数据集的长度, 每种工作状态的每个样本长度设置为400个采样点. 由于各故障数据集采样点数量不一致, 最少为121410最多为122426, 因此全部取前120000采样点, 每个样本长度为400个采样点, 每种工作状态包含300个样本. 按8:2的比例将300个样本分成训练集与测试集进行训练. 训练样本共计1440个, 测试样本共计360个.
| 表 2 滚动轴承故障数据集 |
2.2 实验结果及分析
不同的dropout比率对模型的表现存在一定的影响, 该值取值一般在0.2到0.5之间, 为了选择最佳的dropout比率, 本文对0.2、0.3、0.4、0.5这4个常用比率分别进行了5组实验, 实验结果如图4所示.

|
图 4 不同dropout比率结果对比图 |
如图4所示, 曲线表示不同dropout比率下的模型5组实验预测平均准确率, 柱形表示模型的平均损失值. 实验结果表明dropout比率为0.3时模型平均损失值最低, 且正确率最高, 因此本文模型的dropout比率定为0.3.
本文采用上述模型进行了10次实验, 迭代次数为50次. 10次实验结果表明1D-CNN-LSTM模型在滚动轴承故障诊断问题中最高准确率可达100%, 平均准确率达到了99.833%. 结果如表3所示.
| 表 3 1D-CNN-LSTM模型实验结果 |
第10次实验的训练损失率下降曲线以及正确率曲线如图5所示. 随着训练迭代次数增加, 损失率下降, 准确率逐步上升, 模型表现良好.

|
图 5 训练损失和训练精度 |
为验证本方法在故障诊断精度上的优势, 本文利用相同数据集使用不同的算法模型另外进行了5组对比实验, 每个模型运行5次, 迭代次数均为50, 结果如表4所示. 实验1采用本文所提出的改进1D-CNN-LSTM模型; 实验2采用未改进的1D-CNN-LSTM模型, 该模型CNN与LSTM的连接部分采用了传统的Flatten层和全连接层; 实验3单独使用1D-CNN模型; 实验4单独使用LSTM模型; 实验5单独使用2D-CNN模型; 实验6使用2D-CNN与LSTM组合的模型. 实验结果表名本文所提出的改进1D-CNN-LSTM模型在故障诊断准确率上有最好的表现, 准确率达到了99.83%.
由实验1和实验2对比可以发现, 改进后的1D-CNN-LSTM网络在精度和训练速度都有更好的表现, 通过卷积池化层连接CNN和LSTM两部分网络相对于Flatten层和全连接层来说输入信号的有效特征保留的更加全面, 降维效果也更加优秀; 实验1和实验3结果对比可以看出, 在引入了LSTM后, 模型精度确实有相应提高; 实验1和实验4对比可以发现, 通过卷积操作降低特征图的维度可以大大加快LSTM模型的训练速度; 实验3和实验5对比可以发现, 一维卷积网络在处理一维的滚动轴承振动信号数据方面可以保留更多有效的特征, 在故障诊断精度方面比二维的卷积网络更具优势; 实验1和实验6对比可以看出, 相对与二维卷积网络改良后的一维卷积网络结构可以保留下更多可以被LSTM所提取的时间序列特征, 从而提高模型的诊断精度.
| 表 4 对比实验结果 |
首先通过1D-CNN提取特征并简化特征图维度再输入LSTM进行时序特征提取的方法比直接使用LSTM进行故障诊断训练速度减少了461.35 s. 在引入LSTM后改进的1D-CNN-LSTM模型训练时间仅增加了8.61秒. 实际使用环境中一般采用已训练好的模型对现有故障进行诊断分类, 且对模型精度的要求远高于训练速度, 本文所提出的模型在对包含360个样本的测试集进行诊断分类操作时所需时间不足1 s, 可以满足绝大对数的使用场景要求, 因此相对于精度的提高训练时长的增加是可以接受的.
以上实验分析表明, 采用1D-CNN与LSTM组合的结构, 利用全局最大池化层规避使用Flatten层的操作, 可以有效的保留并利用输入信号的时序特征, 从而提高模型在故障诊断时的精度; 通过1D-CNN提取并简化信号特征, 减少输入LSTM的参数量, 可以有效降低LSTM的训练时间, 增强模型时序特征提取能力. 因此本文所提出的模型改进方案是有意义的.
2.3 不同负载迁移实验为验证改进的1D-CNN-LSTM模型的鲁棒性和泛化能力, 采用迁移学习的方法评估算法模型在不同负载下的迁移适应性, 同时可以解决一部分对训练时间有较高要求的问题.
迁移学习能够学习到以往任务中的知识和经验, 并用于新任务中. 其目的是从一个或多个源任务中抽取知识、经验, 应用于一个新的目标领域中. 本文采用基于参数的迁移学习(parameter-transfer learning): 目标领域和源领域的任务之间共享相同的模型参数. 本次迁移实验通过冻结上文所述在1马力载荷下的1D-CNN-LSTM模型的主要参数从而保留已训练好的模型的特征提取能力, 再添加一层全连接层使其适应目标领域, 并将模型运用到3马力载荷下的轴承故障识别诊断中, 迁移学习模型结构如图6所示.
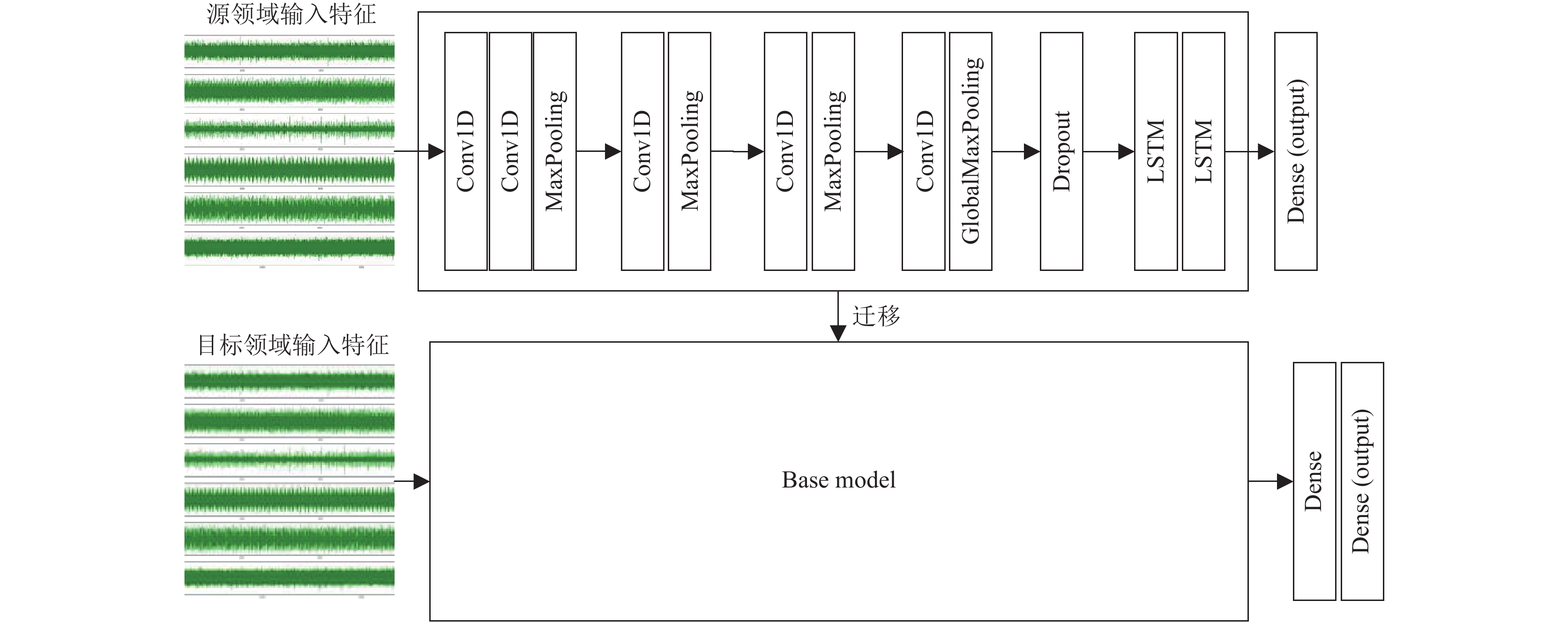
|
图 6 迁移学习模型结构 |
使用迁移学习模型对3马力载荷工况下得滚动轴承信号数据进行故障诊断, 模型所使用的超参数与1马力载荷工况下的相同, 5次实验结果如表5所示, 测试集准确率达99.72%, 表明本文所使用的算法模型在不同工况下仍具有较高准确率, 有较强的泛化能力, 且平均训练用时仅有18.024 s, 相比于源领域训练用时下降了63.13%.
| 表 5 迁移学习实验结果 |
第5次实验的训练损失率下降曲线以及正确率曲线如图7所示. 随着训练迭代次数增加, 损失率平滑下降, 准确率逐步上升, 在15次迭代左右, 故障诊断正确率到达相对稳定状态, 因此考虑通过减少迭代次数到20次迭代, 进一步压缩模型训练时间, 从而适应对模型训练时间有极端要求的场景. 通过实验表明, 在仅20次迭代训练情况下迁移学习模型仍能达到99.72%的故障诊断准确率, 且训练用时仅为8.43 s, 与源领域相比下降了82.76%, 这对紧急情况下的快速故障诊断有着指导性的意义.

|
图 7 迁移学习训练损失和训练精度 |
3 结束语
针对传统CNN以及现在故障诊断算法的不足, 本文提出了基于改进的1D-CNN-LSTM的深度学习算法用于电机滚动轴承的智能化故障诊断. 所提方法改进了传统CNN模型的结构, 引入最大池化层来替代Flatten层和全连接层避免了特征时序特征割裂, 并引入LSTM来提取时序特征. 该方法无需手工特征提取, 端到端的算法结构有较好的可操作性和通用性. 通过对比实验, 验证了该方法故障诊断精度的优越性, 将所提的方法与单一结构的深度学习算法以及基于传统的二维CNN的算法相关算法进行实验对比, 实验结果表明所提方法模型的测试精度方面具有一定优势. 通过迁移学习实验, 缩短了模型训练时间并验证了该算法模型在其他工况下仍有较好的表现, 模型具有较好的泛化能力. 然而, 由于提出的模型网络结构较深, 模型在训练速度上并不具有明显优势. 在以后的研究中将对其进行深入研究, 提高模型的训练速度.
| [1] |
唐立力, 陈国彬. 基于MEA优化BP神经网络的农机滚动轴承故障诊断. 农机化研究, 2019, 41(3): 214-218. DOI:10.3969/j.issn.1003-188X.2019.03.038 |
| [2] |
阳建宏, 黎敏, 丁福焰, 等. 滚动轴承诊断现场实用技术. 北京: 机械工业出版社, 2015. 1–5.
|
| [3] |
Hsiao T, Weng MC. A hierarchical multiple-model approach for detection and isolation of robotic actuator faults. Robotics and Autonomous Systems, 2012, 60(2): 154-166. DOI:10.1016/j.robot.2011.10.003 |
| [4] |
代祥. 基于电网信息物理模型的故障诊断优化模型. 电力学报, 2019, 34(2): 158-166. |
| [5] |
文成林, 吕菲亚, 包哲静, 等. 基于数据驱动的微小故障诊断方法综述. 自动化学报, 2016, 42(9): 1285-1299. |
| [6] |
姚德臣, 杨建伟, 程晓卿, 等. 基于多尺度本征模态排列熵和SA-SVM的轴承故障诊断研究. 机械工程学报, 2018, 54(9): 168-176. |
| [7] |
Peng L, Han GQ, Pagou AL, et al. Electric submersible pump broken shaft fault diagnosis based on principal component analysis. Journal of Petroleum Science and Engineering, 2020, 191: 107154. DOI:10.1016/j.petrol.2020.107154 |
| [8] |
Yang Y, Yu DJ, Cheng JS. A roller bearing fault diagnosis method based on EMD energy entropy and ANN. Journal of Sound and Vibration, 2006, 294(1–2): 269-277. |
| [9] |
Zhou Q, Li YB, Tian Y, et al. A novel method based on nonlinear auto-regression neural network and convolutional neural network for imbalanced fault diagnosis of rotating machinery. Measurement, 2020, 161: 107880. DOI:10.1016/j.measurement.2020.107880 |
| [10] |
雷亚国, 贾峰, 孔德同, 等. 大数据下机械智能故障诊断的机遇与挑战. 机械工程学报, 2018, 54(5): 94-104. |
| [11] |
李国杰, 程学旗. 大数据研究: 未来科技及经济社会发展的重大战略领域——大数据的研究现状与科学思考. 中国科学院院刊, 2012, 27(6): 647-657. DOI:10.3969/j.issn.1000-3045.2012.06.001 |
| [12] |
Hinton GE, Salakhutdinov RR. Reducing the dimensionality of data with neural networks. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647 |
| [13] |
Hinton G, Deng L, Yu D, et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Processing Magazine, 2012, 29(6): 82-97. DOI:10.1109/MSP.2012.2205597 |
| [14] |
Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe, NV, USA. 1097–1105.
|
| [15] |
LeCun Y, Boser B, Denker JS, et al. Backpropagation applied to handwritten zip code recognition. Neural Computation, 1989, 1(4): 541-551. DOI:10.1162/neco.1989.1.4.541 |
| [16] |
LeCun Y, Bengio Y, Hinton G. Deep learning. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [17] |
宫文峰, 陈辉, 张泽辉, 等. 基于改进卷积神经网络的滚动轴承智能故障诊断研究. 振动工程学报, 2020, 33(2): 400-413. |
| [18] |
杜小磊, 陈志刚, 张楠, 等. 基于同步挤压S变换和深度学习的轴承故障诊断. 组合机床与自动化加工技术, 2019(5): 90-93, 97. |
| [19] |
Zhang Y, Tang BP, Han Y, et al. Bearing performance degradation assessment based on time-frequency code features and SOM network. Measurement Science and Technology, 2017, 28(4): 045601. DOI:10.1088/1361-6501/aa56c9 |
| [20] |
Qu XY, Zeng P, Xu CC, et al. RNN-based method for fault diagnosis of grinding system. Proceedings of the IEEE 7th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER). Honolulu, HI, USA. 2017. 673–678.
|
| [21] |
于洋, 何明, 刘博, 等. 基于TL-LSTM的轴承故障声发射信号识别研究. 仪器仪表学报, 2019, 40(5): 51-59. |
| [22] |
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
 2021, Vol. 30
2021, Vol. 30



