高精度武器在现代战争中发挥着越来越重要的作用,高精度制导攻击型武器可以对各种目标实施精确打击, 是我方目标的重要威胁[1], 能有效地对抗高精度制导攻击型武器, 实现对目标的保护是防空系统的重要任务. 防空系统可分为远程防空、中程防空和近程防空三类. 火炮战斗车具有抗干扰能力强、适应性强、火力密集等优点, 是近程防空武器系统的重要组成部分, 其火控系统的精度会直接影响到近程防空系统的防御性能, 所以, 对战斗车火控系统精度进行综合评估, 是评价近程防空武器性能的重要方法[2].
上世纪九十年代, 我国就已经开始了火控系统精度评估的相关研究. 进入新世纪后, 很多学者参与到了火炮瞄准精度评估、火控系统靶试精度评估以及航电武器系统精度评估的工作中[3-6]. 近年来, 有学者根据高炮武器研制需求, 给出了高炮武器总体性能评估方案[7]; 有学者基于节省人力、物力、财力的目的, 研究了基于半实物仿真的精度评估相关技术[8]; 有学者从提高武器系统动态精度角度出发, 设计了基于时间序列的动态精度评估方法[9]. 这些研究工作为解决火控系统精度评估问题提供了思路和方法, 但是对试验调试时如何及时获取试验调试中火控系统实时信息以及如何快速有效的处理大量试验数据以期获得更加精确的系统精度评估数据缺少相应的研究. 本文以集成了火控雷达、光电跟踪设备、火控解算计算机、武器系统、定位定向设备的某型火炮战斗车火控系统为例, 给出了解决试验调试时各设备间通信数据量大、实时性要求高、定位故障困难、获取高精度评估结果困难等问题的精度评估数学模型以及具体的计算方法.
1 需求分析在火控系统试验调试阶段及时了解战斗车各设备的工作状态, 及时定位设备故障, 对各设备产生的数据进行保存以及回放分析可为系统的试验调试节约大量的时间; 自然友好的可视化页面, 简单易懂的使用操作可使非软件开发人员熟练的掌握设备使用方法; 对火控系统中火控雷达、光电跟踪设备测量精度评估以及火控解算计算机解算精度评估、武器随动系统精度评估可以有效的评估火控系统的整体性能.
根据以上分析, 综合评估设备应具有以下功能:
(1)能实时显示火控系统各设备的状态信息、故障信息、测量数据.
(2)能实现对火控系统各设备通信数据的保存、导出、回放.
(3)能对火控雷达和光电跟踪设备测量目标距离、方位角、高低角测量精度评估. 其中光电跟踪通过激光测距, 红外和电视测量方位角和高低角, 对光电跟踪设备的评估可分为激光测距精度评估、红外和电视方位角和高低角精度评估(以下统称光电跟踪精度评估).
(4)能对火控解算计算机解算方位角和高低角、武器随动系统的方位角和高低角精度进行评估.
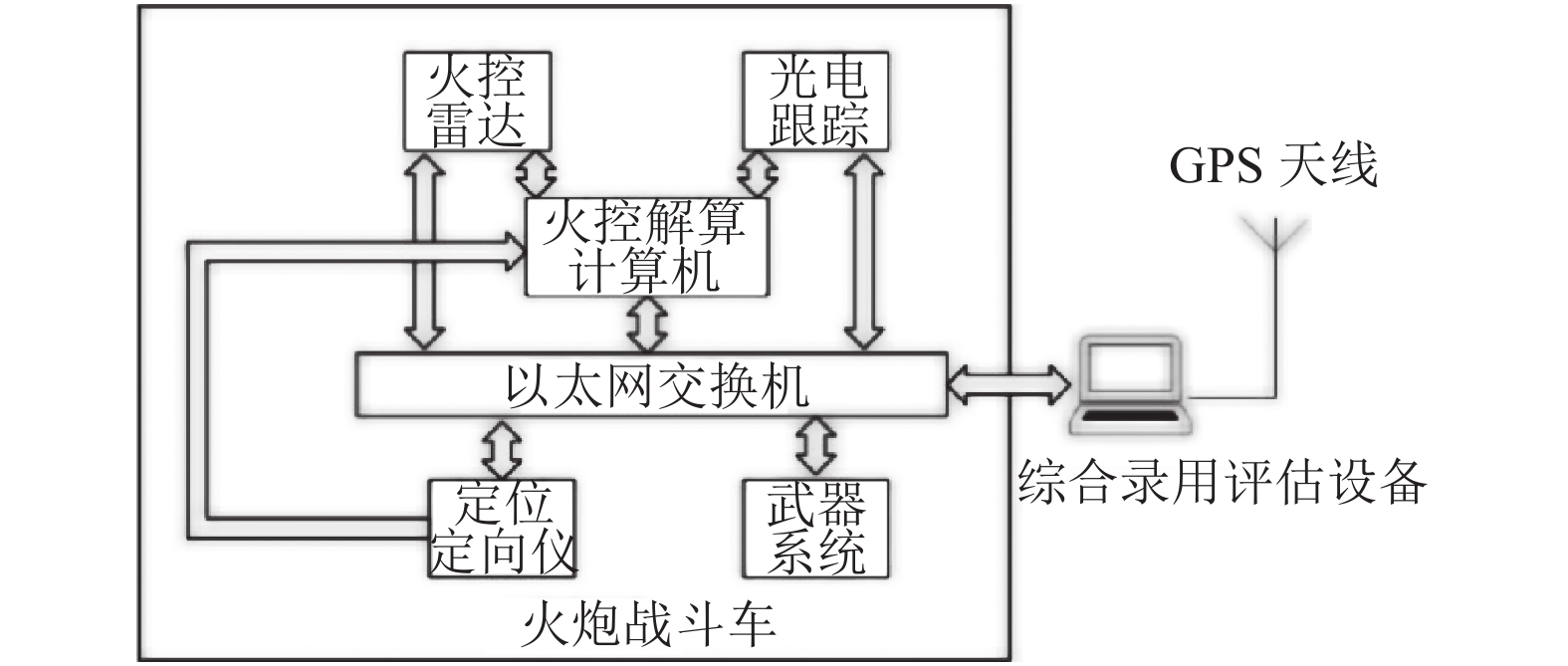
2 数据的录取与保存为了及时获取火控系统各设备通信数据以及精确地对火控系统评估, 综合评估设备需要采集目标的运动状态真值、战斗车各设备的测量数据、解算计算机根据测量数据解算出的诸元值以及武器系统状态值. 实际上, 目标运动状态真值通过试验基地靶机携带的GPS设备获得, 其他数据需要通过综合评估设备来获取, 为了方便后继的数据处理, 需要对综合设备获取的报文附上精确的GPS时标. 战斗车各设备之间通过交换式以太网采用UDP无连接传输协议进行相互通信, 具有数据量大, 速度快的特点, 各设备发送的报文数据都通过交换机, 可将综合评估设备连接至交换机进行各设备数据的捕获. 综合评估设备和战斗车连接框图可用图1表示.
|
图 1 综合评估设备与火炮连接图 |
2.1 数据的录取与显示
在战斗车的以太网中, 各设备以帧为单位进行数据的发送和交换, 交换机基于MAC地址对数据帧进行转发, 将综合评估设备连接至交换机并将其网卡的工作模式设置为混杂模式, 即可实现对所需数据包的捕获. 数据包捕获机制工作在数据链路层, 一般由最底层针对特定操作系统的包捕获机制、最高层针对用户程序的接口和包过滤机制三部分组成[10]. 底层包捕获机制通过操作系统的协议栈访问传输的原始数据包, 高层针对用户程序接口使用户通过简单的函数调用就能获得期望数据包, 包过滤机制实现特定数据包的获取.
WinPcap是Windows平台上应用广泛的第三方数据包捕获机制, 然而WinPcap已经多年无人维护且主要针对Windows XP之前的版本, 已经不适合如今的需求. 可选用Npcap来实现数据包的获取, Npcap是基于WinPcap的数据包捕获机制, 在WinPcap的基础上做了诸多改进.
通过设置Npcap包过滤规则, 可以从战斗车的以太网中获取期望的UDP数据包. 剥去UDP数据包首部, 得到的是火控系统各设备自定义报文, 在自定义报文中, 有发送方和接收方的标识, 根据报文标识可完成报文的识别, 报文识别后, 可调用相应的解析显示函数完成对报文信息的实时解析与显示.
2.2 数据的存放在完成报文解析与显示的同时需要给每个报文头添加GPS时标后将报文保存, 以便后继的报文查看和精度分析. 战斗车各设备以相同频率发送报文, 为了快速存储和保证报文添加GPS时标的精确度, 采用即发即存、按帧存储、二进制格式保存的方式将报文进行存放. 为避免数据帧过长, 可选取某单机设备发送的报文为基准报文, 将两个基准报文之间发送的所有报文作为一帧数据, 基准报文为数据帧的第一个数据包.
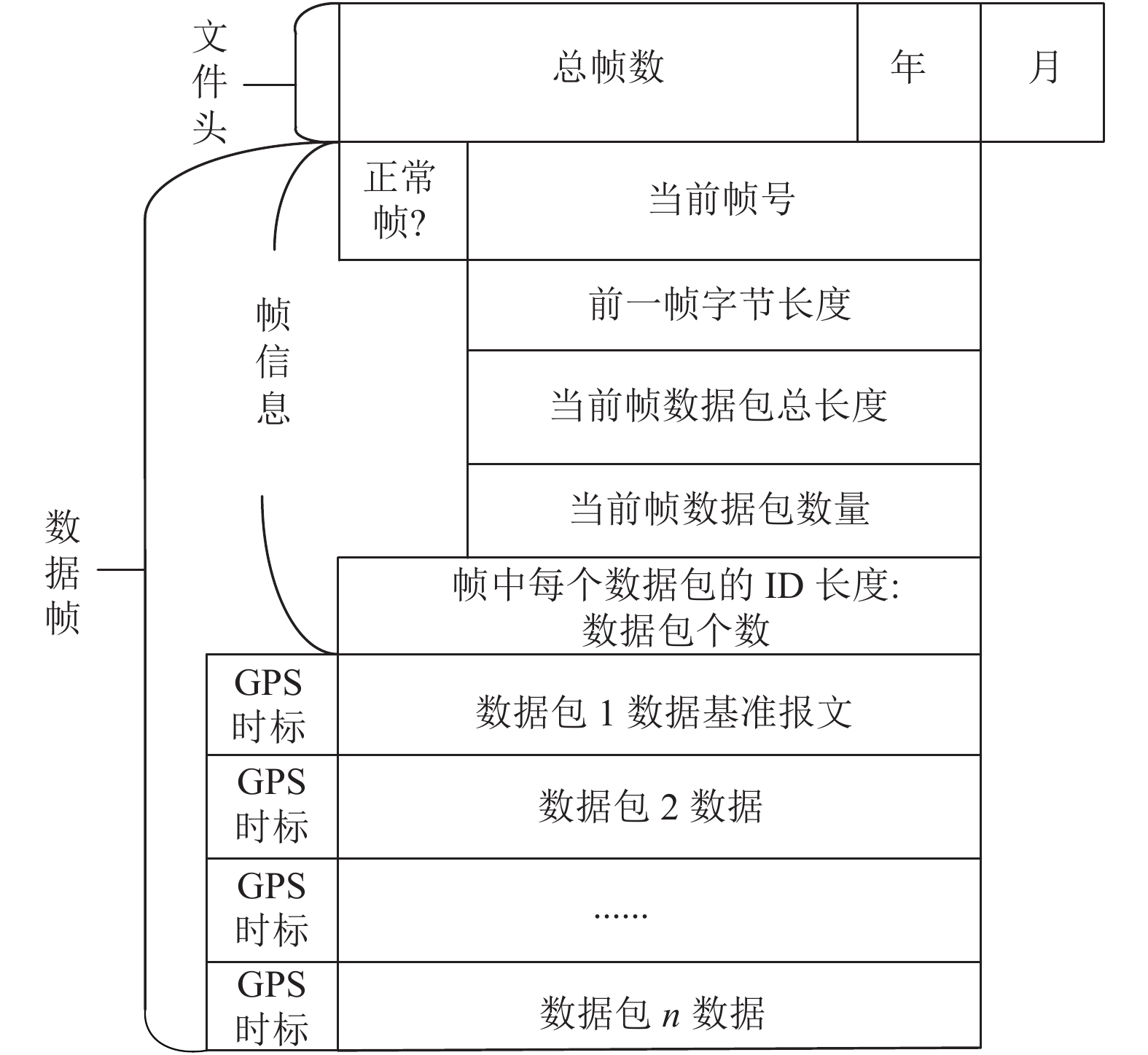
保存报文的文件由文件头和多个数据帧组成, 文件头有6个字节, 前4个字节存储总帧数, 后两个字节分别存储基准年份和月份. 数据帧由帧信息和数据包组成, 帧信息中第一个字节存储该帧是否为正常帧, 当有基准报文时为正常1, 没有基准报文帧长度达到3500个字节时为非正常帧. 其余字节存储当前帧号、前一帧字节长度、当前帧数据包总长度等信息, 由这些信息可以实现快速定位指定帧. 文件存储格式如图2所示.
|
图 2 文件存储格式 |
3 雷达和光电精度评估
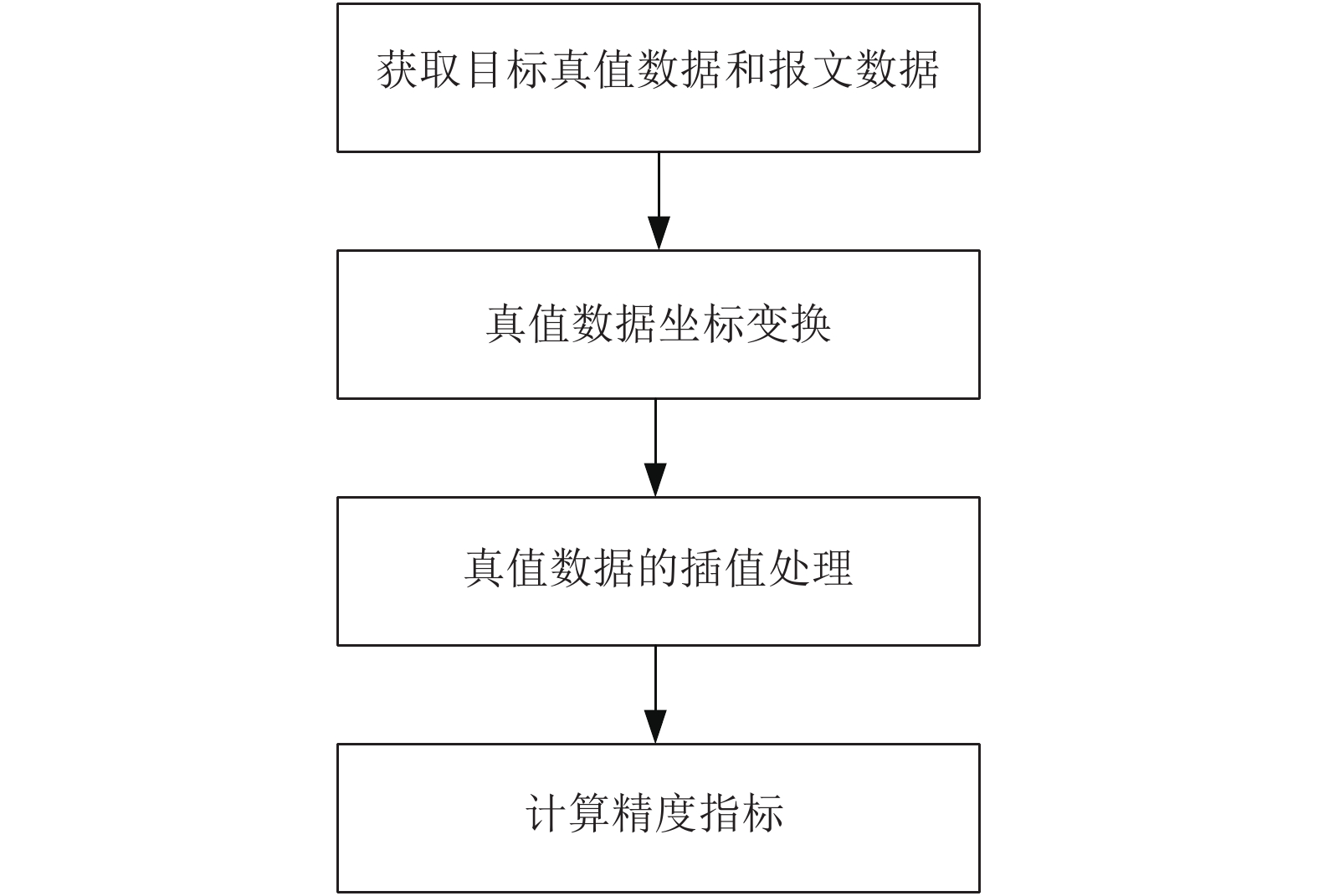
火控雷达和光电设备探测目标的能力取决于雷达的探测精度, 火控雷达和光电设备是火炮战斗车火控系统重要组成部分, 其精度评估是火控系统综合评估的重要内容. 首先对GPS真值数据预处理, 然后经过插值和滤波处理提高真值数据的精度, 最后在同一GPS时标下, 对处理好的真值数据和录取的报文数据进行数据分析和精度统计, 获得火控雷达和光电设备跟踪精度信息. 评估流程如图3所示.
|
图 3 火控雷达和光电评估流程 |
3.1 真值数据坐标变换
真值文件由试验基地提供, 由于不同基地不同设备提供的真值文件格式可能不一样, 为了方便后继数据的处理, 需要将试验基地提供的以原始大地坐标系(大地经度L, 大地纬度B, 大地高H)下的真值文件转换为站心坐标系[11](EUN)最后转换成以雷达(光电)回转中心为原点的坐标.
假设一真值点在大地坐标系下坐标为
| $ \left[\begin{array}{c}x\\ y\\ {\textit{z}}\end{array}\right]= \left[\begin{array}{c}(N+h)\cos\mu \cos\varphi \\ (N+h)\cos\mu \sin\varphi \\ \left[N\left(1-{e}^{2}\right)+h\right]\sin\mu \end{array}\right]$ | (1) |
其中,
| ${e^2} = \left( {{a^2} - {b^2}} \right)/{a^2} = 0.006\;694\;379\;99$ |
其中, a = 6378137±2 m, 为大地坐标系椭球的长半轴; b = 6356752.3142 m, 为大地坐标系椭球的短半轴.
若标定点的大地原始坐标系中的坐标为
| $ \left[\begin{array}{c}e\\ n\\ u\end{array}\right]=M\left[\begin{array}{c}x-{x}_{0}\\ y- {y}_{0}\\ {\textit{z}}-{{\textit{z}}}_{0}\end{array}\right]$ | (2) |
其中,
| $M = \left[ {\begin{array}{*{20}{c}} { - \sin \varphi_0 }&{\cos \varphi_0 }&0 \\ { - \sin \mu_0 \cos \varphi_0 }&{ - \sin \mu_0 \sin \varphi_0 }&{\cos \mu_0 } \\ {\cos \mu_0 \cos \varphi_0 }&{\cos \varphi_0 \sin \varphi_0 }&{\sin \varphi_0 } \end{array}} \right]$ |
如图4所示, 真值点T在站心坐标系坐标点为
| $ \left[\begin{array}{c}{x}_{T}\\ {y}_{T}\\ {{\textit{z}}}_{T}\end{array}\right]= \left[\begin{array}{ccc}\mathrm{cos}\theta & -\mathrm{sin}\theta & 0\\ \mathrm{sin}\theta & \mathrm{cos}\theta & 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}e\\ n\\ u\end{array}\right]\rm{+}\left[\begin{array}{c}\Delta x\\ \Delta y\\ \Delta {\textit{z}}\end{array}\right]$ | (3) |

|
图 4 站心坐标向武器托架中心坐标转换 |
最后, 根据武器托架中心和雷达(光电)中心的位置关系, 将真值数据转化为以雷达(光电)中心为原点的球坐标系.
3.2 真值数据的插值处理真值的频率和录取的数据频率不同, 导致真值的时标和录取数据的时标不同, 需要将真值时标和录取数据时标对齐, 确保真值和录取数据都是同一时刻下的数据. 由于真值频率小, 时标对齐时需要对真值数据进行拟合. 综合考虑拟合真值精度、占用内存以及处理时间等因素, 选用20点最小二乘法进行二次曲线真值拟合.
假设二次曲线拟合多项式为:
| $ f\left(x\right)= {a}_{0}+{a}_{1}x+{a}_{2}{x}^{2}$ | (4) |
选取某一录取数据时标为拟合时刻
| ${R^2} = \sum\limits_{i = - 10,i \ne 0}^{10} {{{\left[ {{y_i} - \left( {{a_0} + {a_1}{x_i} + {a_2}x_i^2} \right)} \right]}^2}} $ | (5) |
对上式求
| $ XA= Y $ | (6) |
其中,
| $ X= \left[\begin{array}{ccc}20& { \displaystyle\sum\limits _{i=-10,i\ne 0}^{10}{x}_{i}}& {\displaystyle \sum\limits _{i=-10,i\ne 0}^{10}{x}_{i}^{2}}\\ { \displaystyle\sum\limits _{i=-10,i\ne 0}^{10}{x}_{i}}& { \displaystyle\sum \limits_{i=-10,i\ne 0}^{10}{x}_{i}^{2}}& { \displaystyle\sum\limits _{i=-10,i\ne 0}^{10}{x}_{i}^{3}}\\ { \displaystyle\sum\limits _{i=-10,i\ne 0}^{10}{x}_{i}^{2}}& {\displaystyle \sum \limits_{i=-10,i\ne 0}^{10}{x}_{i}^{3}}& {\displaystyle\sum\limits _{i=-10,i\ne 0}^{10}{x}_{i}^{4}}\end{array}\right]$ |
| $Y = {\left[ {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{i = - 10,i \ne 0}^{10} {{y_i}} }&{\displaystyle\sum\limits_{i = - 10,i \ne 0}^{10} {{x_i}{y_i}} }&{\displaystyle\sum\limits_{i = - 10,i \ne 0}^{10} {x_i^2{y_i}} } \end{array}} \right]^{\rm{T}}}$ |
| $A = {\left[ {\begin{array}{*{20}{c}} {{a_0}}&{{a_1}}&{{a_2}} \end{array}} \right]^{\rm{T}}}$ |
则通过
可将以上处理看成如图5的窗处理, 不断的改变

|
图 5 目标真值数据拟合 |
3.3 精度指标计算
对火控雷达和光电跟踪精度的评估通过火控雷达和光电跟踪测量目标距离d、方位角
系统误差可表示为:
| $\bar \beta = \frac{1}{n}\sum\limits_{i = 1}^n {\Delta {\beta _i}} $ | (7) |
随机误差可表示为:
| ${S_\beta } = \sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {\left( {{\beta _i} - \bar \beta } \right)} } $ | (8) |
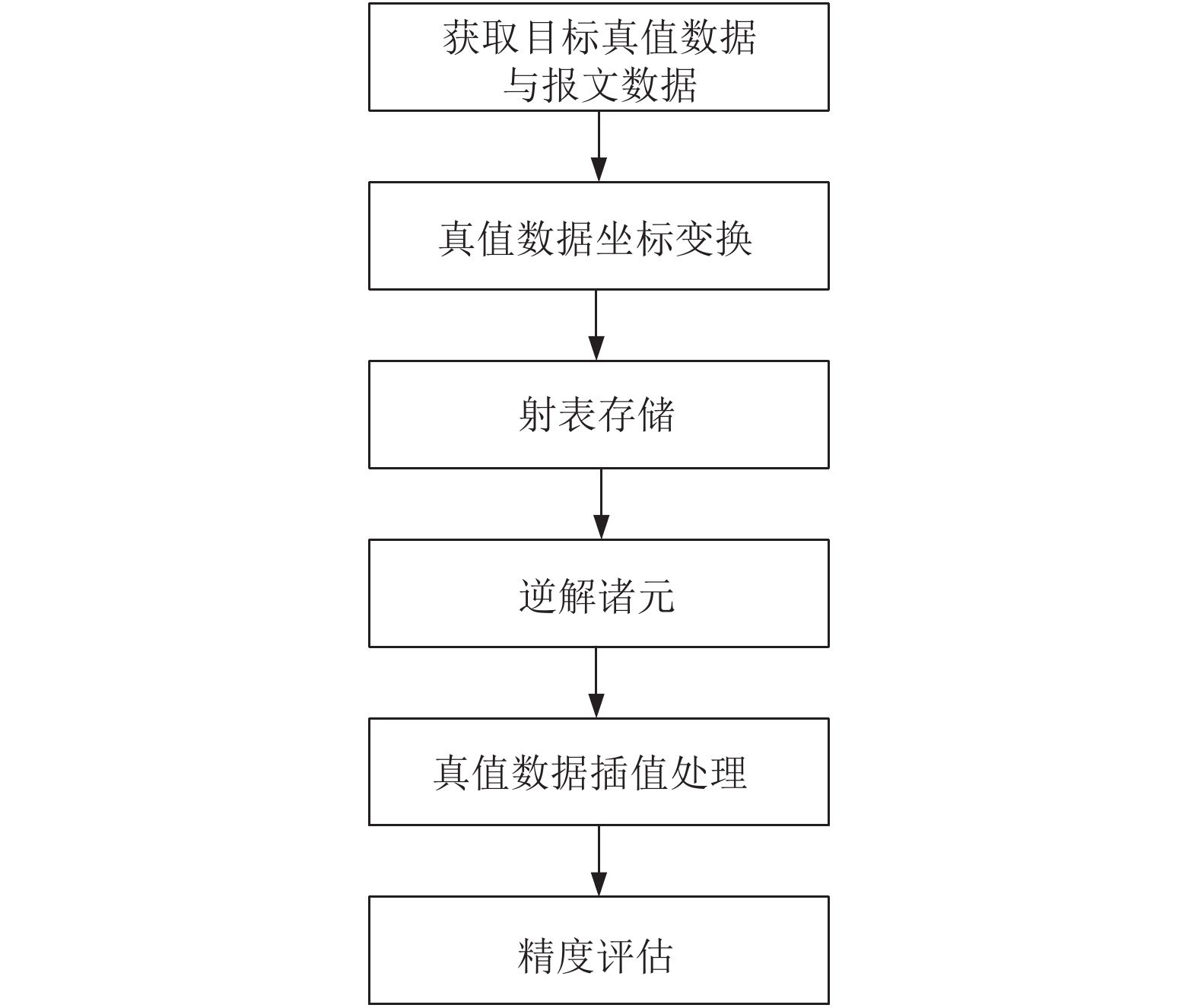
火控解算精度和武器系统精度直接关系到战斗车对目标的打击精度, 是评价火炮战斗车火控系统性能优劣的重要指标之一, 同样也是火控系统精度分析的重要组成部分. 其评估流程如图6所示.
|
图 6 火控解算和武器系统评估流程 |
4.1 射表存储
将弹道方程的数字解按照便于查找射击诸元的格式形成的数字表格称为射表. 将试验基地提供的射表采用Access数据库按照基本表和修正表分类存储, 使用时, 可通过目标的距离和高度来确定射表中的弹道数据.
4.2 逆解诸元[12]对火控解算和武器系统精度评估是在已知目标航路真值信息下进行, 因此使用逆解法求解某时刻
如图7假设已知航路上一点A, 记时刻
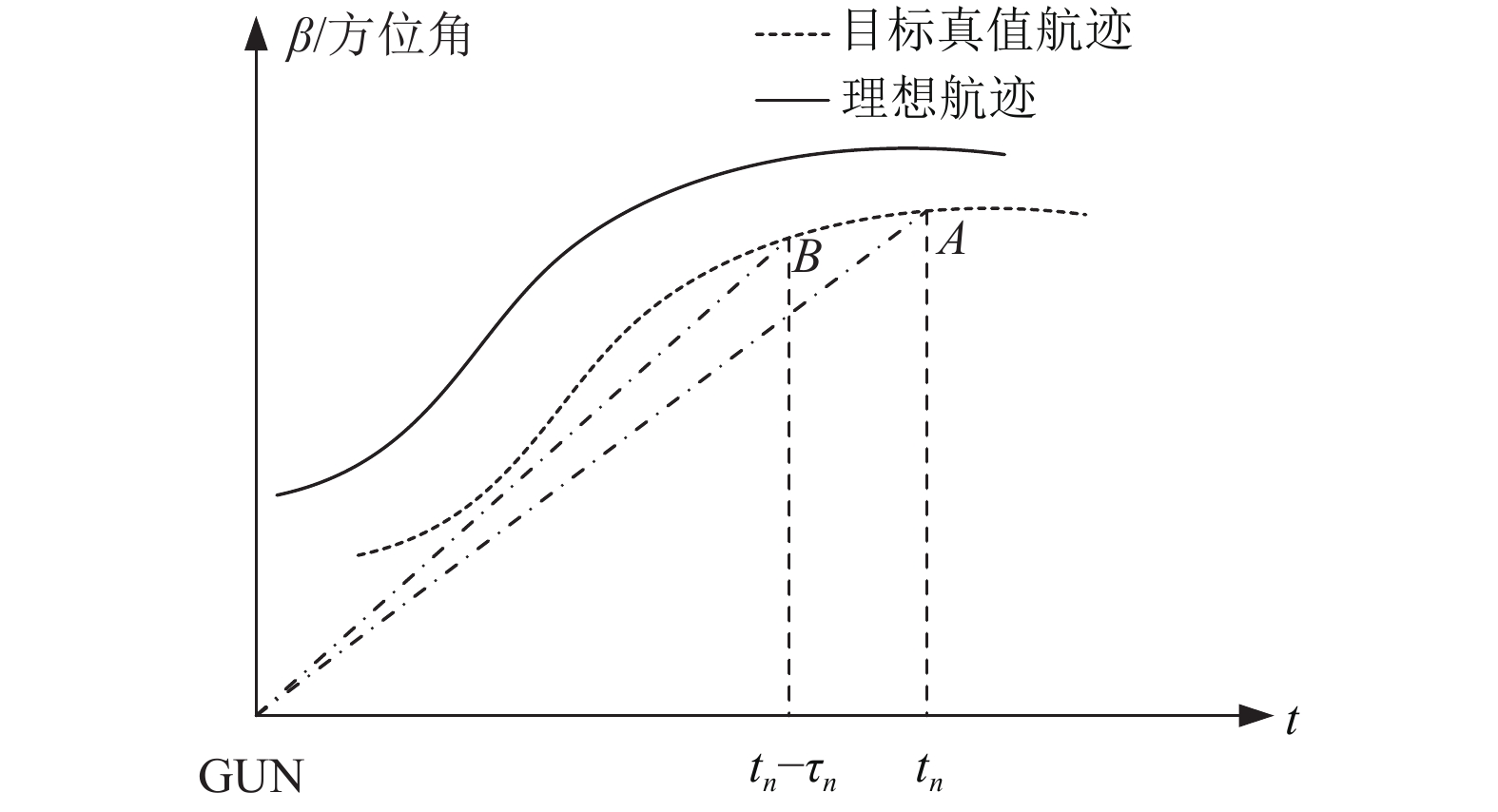
|
图 7 逆解法示意图 |

|
图 8 基本表数据的4次三点插值示意图 |
4.3 数据的插值处理
根据逆解法原理可以求出每个
| 表 1 逆解法Tn时刻对应数据表 |
已知
在平面有
| $ {L}_{n}\left(x\right)= \sum \limits_{j=0}^{n}\left( {{y}_{i} \prod \limits_{i=0,i\ne j}^{n}\frac{x-{x}_{i}}{{x}_{j}- {x}_{i}}} \right)$ | (9) |
使
对火控解算和武器系统的评估通过火控解算和武器系统方位角
| $ \Delta {\beta _i} = {\beta _i} - {\beta _{0i}}\;(i = 1,\;2,\;3,\cdots,\;n). $ |
系统误差可表示为:
| $\bar \beta = \frac{1}{n}\sum\limits_{i = 1}^n {\Delta {\beta _i}} $ | (10) |
随机误差可表示为:
| ${S_\beta } = \sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {\left( {{\beta _i} - \bar \beta } \right)} } $ | (12) |
一套完整评估设备的硬件包括定制专用计算机(含航插接口、千兆网口、RS232串口、PCI-e接口)、GPS同步授时仪(含同步时钟卡、天线)、双绞线. 设备使用时, 通过双绞线将专用计算机连接至火炮战斗车的以太网交换机上, 将GPS同步时钟卡以及GPS天线连接至专用计算机.
5.2 软件实现软件部分是整个综合评估设备的核心, 它需要采集报文并对报文进行处理, 从需求分析可以看出, 综合评估设备的软件部分需实现以下功能:
(1) 对战斗车各设备发送的报文进行解析与录取存放, 并将解析结果实时显示.
(2) 支持离线解析录取的报文信息, 即实现对报文的回放.
(3) 支持对报文数据进行不同状态查询, 支持设置查询范围.
(4) 支持火控雷达、光电跟踪设备的测量精度评估, 火控解算系统解算精度评估, 武器系统控制精度评估, 并支持将评估结果显示与导出.
软件设计总体功能模块如图9所示.

|
图 9 软件的总体功能模块 |
数据录取界面设计如图10, 页面采用多标签页设计, 分别显示不同设备的状态与数据信息; 在综合页面显示各设备与综合评估设备的通信状态、设备故障、设备工作方式以及设备的重要数据信息. 这些设计, 不仅方便了用户快速掌握设备的重要信息还保证了对各设备信息显示的完整性.

|
图 10 数据录取页面 |
某次试验指挥仪-雷达过程回放如图11所示, 经与指挥台数据对比, 回放页面正确显示出各状态信息和数据信息. 在过程回放页面用户通过选择设备标签查看各单机设备信息, 可以快速了解设备工作状态, 定位设备故障. 在右侧的回放控制中, 可以逐帧回放也可以选择不同速率回放.

|
图 11 某次试验指挥仪-雷达的过程回放 |
在精度评估界面, 可进行气象数据、火炮参数、火炮相对于雷达光电中心坐标等参数的设置, 通过不同的待评估报文和真值数据在设置参数的影响下生成评估文件并可对评估文件进行精度分析. 评估的项目有雷达测距系统误差和随机误差; 雷达方位角、高低角、径向速度的系统误差和随机误差; 火控解算、武器系统的方位角和高低角的系统误差和随机误差; 红外、电视的方位角和高低角系统误差和随机误差等. 图12为某次试验数据精度评估数据输出结果.
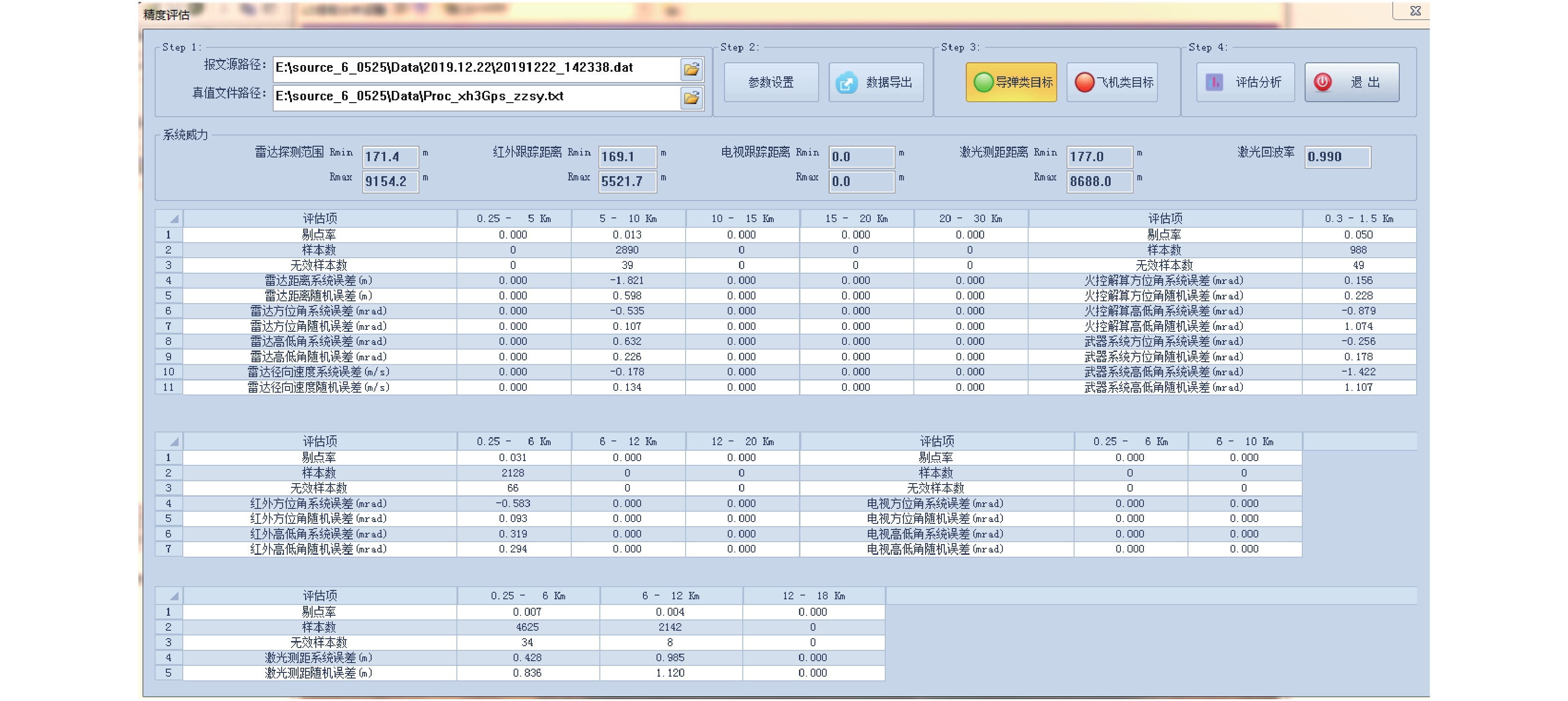
|
图 12 某次试验精度评估结果 |
6 结束语
本文从理论上分析了火炮战斗车火控系统精度评估的过程, 阐述了各单机设备精度评估数学模型建立的过程以及具体的计算方法. 通过对战斗车单机设备通信特点以及试验调试过程中实际需求的分析, 本文设计并实现了战斗车火控系统综合评估设备, 该设备方便了用户在战斗车试验过程中对战斗车各设备状态的掌握. 通过分析综合评估设备计算出的精度数据, 不仅可以准确的判断各单机设备是否符合设计要求, 还能综合评价战斗车火控系统的总体性能. 目前, 该设备已经应用于某型战斗车的试验调试阶段, 有效的缩短了试验调试时间, 提高了该型号战斗车的生产效率.
| [1] |
赵思勇. 高炮火控系统试验数据采集与统计分析研究[硕士学位论文]. 南京: 南京理工大学, 2007.
|
| [2] |
刘正, 刘斌胜. 某型车载遥控武器站火控系统精度仿真分析. 计算机仿真, 2013, 30(4): 9-12. DOI:10.3969/j.issn.1006-9348.2013.04.003 |
| [3] |
袁慧馨. 空空导弹火控系统靶试精度评估技术研究. 电光与控制, 2006, 13(6): 64-67. DOI:10.3969/j.issn.1671-637X.2006.06.017 |
| [4] |
徐国亮, 冷述振. 舰炮武器系统对大目标跟踪精度评估修正方法. 火力与指挥控制, 2007, 32(5): 125-128. DOI:10.3969/j.issn.1002-0640.2007.05.036 |
| [5] |
刘立欣, 刘亦菲, 李杰. 基于CCD的火炮瞄准射击精度评估系统. 第七届全国信息获取与处理学术会议论文集. 桂林, 中国. 2009. 652–654.
|
| [6] |
刘军, 周德云, 张堃, 等. 航电武器系统精度评估研究. 计算机仿真, 2010, 27(1): 71-75. DOI:10.3969/j.issn.1006-9348.2010.01.027 |
| [7] |
舒立鹏, 丁天宝, 王峰, 等. 高炮武器总体性能评估软件研究. 火炮发射与控制学报, 2017, 38(4): 30-34. |
| [8] |
韩洁, 杜会盈, 毛洪川, 等. 基于半实物仿真的精度评估技术. 科技传播, 2018, 10(11): 99-101. DOI:10.3969/j.issn.1674-6708.2018.11.055 |
| [9] |
刘德耀, 韩旭, 普仕凡. 基于时间序列模型的舰炮武器系统动态精度评估方法. 南京理工大学学报, 2018, 42(1): 18-25. |
| [10] |
郭凯. 基于WinPcap的数据包捕获系统的设计与实现[硕士学位论文]. 西安: 西安电子科技大学, 2013.
|
| [11] |
黄立人, 高砚龙, 任立生. 关于NEU(ENU)坐标系. 大地测量与地球动力学, 2006, 26(1): 97-99. |
| [12] |
薄煜明, 郭治, 钱龙军, 等. 现代火控理论与应用基础. 北京: 科学出版社, 2012.132–133.
|
 2021, Vol. 30
2021, Vol. 30



