科学与工程领域的大多数优化问题本质上都是“多模态”的, 这类问题被称为多模态优化问题, 其特点是目标函数同时具有多个全局最优解或局部最优解. 传统使用的求解方法在求解MMOPs时须反复计算多次, 才有可能找到不同的最优解, 这样既费时又费力. 因此, 寻找可行有效的求解MMOPs的新算法一直以来备受广大科技工作者的关注[1-4]. 为此, 许多被称为小生境的技术包括拥挤[5]、共享[6]、聚类[7]、物种[8]和种群拓扑[9]等被提出. 小生境的主要思想是将整个种群划分为几个小生境(亚种群), 每个亚种群集中于寻找一个或几个最优值.
差分进化算法(Differential Evolution, DE)[10]是由Storn和Price在1995年提出的一种全局优化启发式算法. 由于其简单、有效, 已被用于处理各种各样的优化问题, 例如全局优化问题[11], MMOPs[12], 多目标优化问题[13]等. 近年来,一些基于小生境的DE变体[14-18]被提出以处理MMOPs, 但是, 这些方法在最优解数量大、维度高和复杂性高的时候效果往往不太理想.
本文提出了一种基于邻域低密度个体的差分进化算法(Low Density Points Differential Evolutionary, LDPDE)求解MMOPs. 算法在每一代, 首先使用密度峰值聚类的方法求得每一个个体的密度, 然后, 优先对邻域范围密度低于当前个体的目标个体进行突变操作, 随着种群的进化, 种群个体逐渐收敛到小生境中心, 进化过程将会自动的从探索阶段转化为收敛阶段, 进而平衡算法的探索与收敛能力. LDPDE算法的主要特点有: (1) LDPDE是一种基于距离的小生境方法, 它可以通过邻域范围内个体的密度变化达到算法探索与收敛之间的平衡. (2) 提出了一种新的DE变异算子, 称为DE/low-density/1, 该算子在算法的探索阶段可以寻找尽可能多的有效个体.
1 差分进化算法考虑优化模型:
| $\mathop {\min }\limits_{x \in \Omega \subseteq {R^n}} f(X)$ | (1) |
其中,
差分进化算法是一种简单有效的全局优化启发式算法. 与其他进化算法类似, DE有4个步骤: 初始化、变异、交叉和选择. 标准的DE算法过程如下:
(1) 初始化
首先, DE从最小和最大界限约束的搜索空间内对个体进行均匀随机化, 可以表示为:
| $x_{i,n}^j = x_{\min }^j + rand(0,1) \cdot \left( {x_{\max }^j - x_{\min }^j} \right)$ |
其中,
(2) 变异
初始化后, 从当前种群中随机选择的个体经过变异算子产生突变个体
| ${v_i} = {x_{r_1^i,n}} + F \cdot \left( {{x_{r_2^i,n}} - {x_{r_3^i,n}}} \right)$ |
其中,
(3) 交叉
交叉算子通过重新组合目标个体
| $u_i^j = \left\{ {\begin{array}{*{20}{l}} {v_i^j},&{rand < Cr \vee j = {j_{rand}}} \\ {x_{i,n}^j},&{\rm otherwise} \end{array}} \right.$ |
其中,
(4) 选择
选择运算符确定目标或实验个体是否进入到下一代. 如果新的实验个体的函数值等于或小于目标个体的函数值, 它将替换相应的目标个体. 下一代
| ${x_{i,n + 1}} = \left\{ {\begin{array}{*{20}{l}} {{u_i}},&{f({u_i}) \le f({x_{i,n}})} \\ {{x_{i,n}}},&{f({x_{i,n}}) < f({u_i})} \end{array}} \right.$ |
最后, DE继续执行变异、交叉和选择运算符, 直到满足终止条件为止. 算法1中以伪代码的形式给出了标准DE的算法过程.
算法1. 标准差分进化算法(DE)
输入: 目标函数(最小值)f(x); 比例因子F; 交叉率Cr; 种群大小NP; 进化代数MaxIt.
1) 随机初始化种群
2)
3)
4)
5)
6)
7)
8)
9)
10)
11) 输出
密度峰值聚类[19]是一种简单有效的快速聚类方法, 由Rodriguez和Laio[20]通过发现潜在簇的密度峰值提出. 对于每个数据点
数据点
| $\rho (i) = \sum\limits_{j \in {I_S}\backslash \{ i\} } {{{\rm e}^{ - {{\left( {\textstyle\frac{{{d_{ij}}}}{{{d_c}}}} \right)}^2}}}} $ | (2) |
其中,
| $\psi (i) = \sum\nolimits_{j = 1}^n {{{\rm e}^{ - {{\left( {\textstyle\frac{{\left\| {x(i) - x(j)} \right\|}}{\sigma }} \right)}^2}}}} $ | (3) |
则熵H为:
| $H = - \sum\nolimits_{i = 1}^n {\frac{{\psi (i)}}{{\textit{z}}}\log \left( {\frac{{\psi (i)}}{{\textit{z}}}} \right)} $ | (4) |
其中, 归一化因子z为:
| ${\textit{z}} = \sum\nolimits_{i = 1}^n {\psi (i)} $ | (5) |
现在只要找到使得H值最小的
为了解决多模态优化问题, 许多策略被提出并将嵌入到DE中. 以下将简要介绍与DE相结合的各种策略.
(1) 拥挤(CDE): 文献[14]将拥挤方案和健身共享嵌入到DE中, 分别形成CDE算法和SharingDE算法. 在CDE算法中, 对于每个子代个体, 通过在父代种群中随机选择C个父代个体, 然后将子代与该群体中最相似(欧氏距离最近)的父代进行比较. 如果子代更好, 它将取代该种群中最相似的父代个体. 否则, 子代个体将被遗弃. SharingDE算法则利用共享方案来防止种群收敛到同一个高峰.
(2) 物种(SDE): 在SDE算法[15]中, 根据个体的适宜性和小生半径r将整个种群分为几个物种. 每个物种都有一个具有最佳适应性的物种种子, 并且DE运算符只在当前物种种群内执行. 然后将生成的N个子代个体与N个父代个体合并为一个种群, 从合并种群中选择N个最佳个体, 形成一个新的种群.
(3) 聚类: Qu等[16]提出了嵌入到CDE算法和SDE算法中的邻域突变策略(包括NCDE和NSDE)中, DE运算符在每个个体的欧几里得邻域中执行. 遵循这一思想, Gao等[17]提出了一种具有自适应策略(包括self-CCDE和CSDE)的聚类DE, 它采用自适应参数控制来增强DE的搜索能力. Zhang等[18]提出了一种新的基于位置敏感哈希的小生境技术以降低时间复杂度, 并将其应用于NCDE中, 称为Fast-NCDE算法.
以上这些方法在处理MMOPs问题时已经显示出各方面的有效性, 但它们也有一定的缺点. 一方面, 随着MMOPs问题全局最优解的数量增加, 这些方法将全部最优值点找到的机会就越小; 另一方面, 在解决具有高维度和高复杂性的MMOPs时, 几乎所有这些固定方法都会失效. 因此, 为解决高维度和高复杂性的MMOPs, 许多其他基于DE的多模态算法被提出. Biswas等[22]提出了一种新的信息共享机制, 该机制使用本地信息矩阵来诱导有效的利基行为, 称为LoINDE算法(包括LoICDE算法和LoISDE算法). 同时, 他们还提出了一种新的以父代为中心的标准化邻域(PCNN)变异算子, 以维持多个最优值, 称为PNPCDE算法[23]. Wang等[24]提出了是一种基于距离的小生境方法, 称为MSTDE算法, 通过DPR策略切割少量大的加权边来形成多个小生境, 平衡收敛性和多样性.
3 基于低密度的差分进化算法在本节中, 我们将提出基于密度峰值的差分进化算法(LDPDE).
3.1 基于孤立个体的变异算子受文献[25]启发, 提出一种用于多模态优化的新DE变异算子, 称为DE/low-density/1. 该算子的主要特征是它在当前个体邻域中随机选择密度低于当前个体的个体作为变异算子的目标个体, 因此, 目标个体可以被选择变异算子迁移到隔离区域. 在典型的小生境方法中, 同一山谷中的个体倾向于通过在山谷中下降聚集在一起. 而在本文提出的方法中, 个体积极地迁移到其他山谷. DE/low-densit/1中使用的变异算子描述如下:
| ${v_i} = x_{r_1^p,n}^{\rm near} + {F_1} \cdot \left( {{x_{r_2^i,n}} - x'_{r_2^i,n}} \right)$ | (6) |
其中,
当
| ${v_i} = x_{r_1^i,n}^{\rm near} + {F_2} \cdot \left( {x'_{r_2^i,n} - x'_{r_3^i,n}} \right)$ | (7) |
其中,
如图1所示[25], 图1(a)为邻域变异算子的行为特征, 图1(b)为基于孤立个体的变异算子的行为特征. 基于孤立个体的变异算子可以促使种群个体向孤立个体附近迁移, 提高算法的多模态开发能力, 而邻域变异算子只在小生境内进行, 避免差分进化的贪婪原则带来的错误替换, 提高算法的收敛性.
将以上两种变异操作结合形成的改进的变异算子描述如下:
| $ {v_i} = \left\{ {\begin{array}{*{20}{l}} {x_{r_1^p,n}^{\rm near} + {F_1} \cdot \left( {{x_{r_2^i,n}} - x'_{r_2^i,n}} \right)},&{find(i){\text{非空}}}\\ {x_{r_1^i,n}^{\rm near} + {F_2} \cdot \left( {x'_{r_2^i,n} - x'_{r_3^i,n}} \right)},&{\rm otherwise} \end{array}} \right.$ | (8) |
随着种群的进化,

|
图 1 两种变异算子的行为特征 |
LDPDE的算法过程的伪代码的在算法2给出.
算法2. 基于邻域低密度个体的差分进化算法(LDPDE)
输入: 目标函数(最小值)f(x); 比例因子F; 交叉率Cr; 种群大小NP; 最大计算次数MaxFEs; 邻域大小
1) 随机初始化种群
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
21)
22)
23) 输出
本文采用了CEC2013测试套件[26]中所有20种常用的多模态测试函数来评估LDPDE的性能, 该测试套件中的测试函数具有各种不同的特征, 这使实验更加全面且令人信服. 下面对这20个基准测试函数作简要说明.
F1: Five-Uneven-Peak Trap(1D),
| $F1(x) = \left\{ {\begin{array}{*{20}{l}} {80(2.5 - x)},&{0 \le x < 2.5} \\ {64(x - 2.5)},&{2.5 \le x < 5.0} \\ {64(7.5 - x)},&{5.0 \le x < 7.5} \\ {28(x - 7.5)},&{7.5 \le x < 12.5} \\ {28(17.5 - x)},&{12.5 \le x < 17.5} \\ {32(x - 17.5)},&{17.5 \le x < 22.5} \\ {32(27.5 - x)},&{22.5 \le x < 27.5} \\ {80(x - 27.5)},&{27.5 \le x \le 30} \end{array}} \right.$ |
F2: Equal Maxima(1D),
| ${F_2}(x) = {\sin ^6}(5\pi x)$ |
F3: Uneven Decreasing Maxima(1D),
| $F3(x) = {\operatorname{e} ^{ - 2\log (2){{\left( {\textstyle\frac{{x - 0.08}}{{0.853}}} \right)}^2}}}{\sin ^6}\left( {5\pi \left( {{x^{{3 / 4}}} - 0.05} \right)} \right)$ |
F4: Himmelblau(2D),
| $F4({x_1},{x_2}) = 200 - {\left( {x_1^2 + {x_2} - 11} \right)^2} - {\left( {{x_1} + x_2^2 - 7} \right)^2}$ |
F5: Six-Hump Camel Back(2D),
| $F5\left( {{x_1},{x_2}} \right) = - 4\left[ {\left( {4 - 2.1x_1^2 + \frac{{x_1^4}}{3}} \right)x_1^2 + {x_1}{x_2} + \left( {4x_2^2 - 4} \right)x_2^2} \right]$ |
F6, F8: Shubert(2D, 3D),
| $F6,8\left( {\overrightarrow x } \right) = - \prod\nolimits_{i = 1}^D {\sum\nolimits_{j = 1}^5 {j\cos \left[ {(j + 1){x_i} + j} \right]} } $ |
F7, F9: Vincent(2D, 3D),
| $F7,9\left( {\overrightarrow x } \right) = \frac{1}{D}\sum\nolimits_{i = 1}^D {\sin (10\log ({x_i}} ))$ |
F10: Modified Rastrigin-All Global Optima(2D),
| $F10\left( {\overrightarrow x } \right) = - \sum\limits_{i = 1}^D {(10 + 9\cos (2\pi {k_i}} {x_i}))$ |
其中,
剩下的10个函数为4个复合函数在不同维度大小的情况, 把4个函数简称为
F11: CF1(2D). 全局最优点数量为6.
F12: CF2(2D). 全局最优点数量为8.
F13, F14, F16, F18: CF3(2D, 3D, 5D, 10D). 全局最优点数量为6.
F15, F17, F19, F20: CF4(3D, 5D, 10D, 20 D). 全局最优点数量为8.
将LDPDE与几种基于DE的多模态算法进行比较, 包括CDE算法, SDE算法, NCDE算法, NSDE算法, LoICDE算法, LoISDE算法, PNPCDE算法, Fast-NCDE算法和MSTDE算法. 这些算法横跨从2004年到2019年的时间间隔. 此外, 为了具有可比性, 所有对比算法的参数配置都与原始论文中的设置相同.
4.2 参数设置LDPDE中的放大系数
| 表 1 参数设置 |
LDPDE中的种群规模、最大计算次数MaxFEs和比较算法的结果参考自文献[24]. 所有的结果都是在同一测试套件中使用相同的MaxFEs下得到的, 每种算法均运行51次以进行统计并避免随机性.
对于给定的MaxFEs在精度水平
表2列出了LDPDE与其他多模态算法在F1–F20上PR和SR的详细比较结果. 为了结果清晰, 最佳PR果用黑体标出. 符号"+"、"−"和"
| 表 2 LDPDE与其他多模态算法在F1–F20上PR和SR的详细比较结果 |
从表2可以看到LDPDE在所有函数上都表现很好. 对于简单函数
多模态函数
总之, LDPDE在所有20个函数上与CDE, SDE, NCDE, NSDE, LIPS, LoICDE, LoISDE, PNPCDE, self-CCDE, self-CSDE, fast-NCDE和MSTDE算法相比
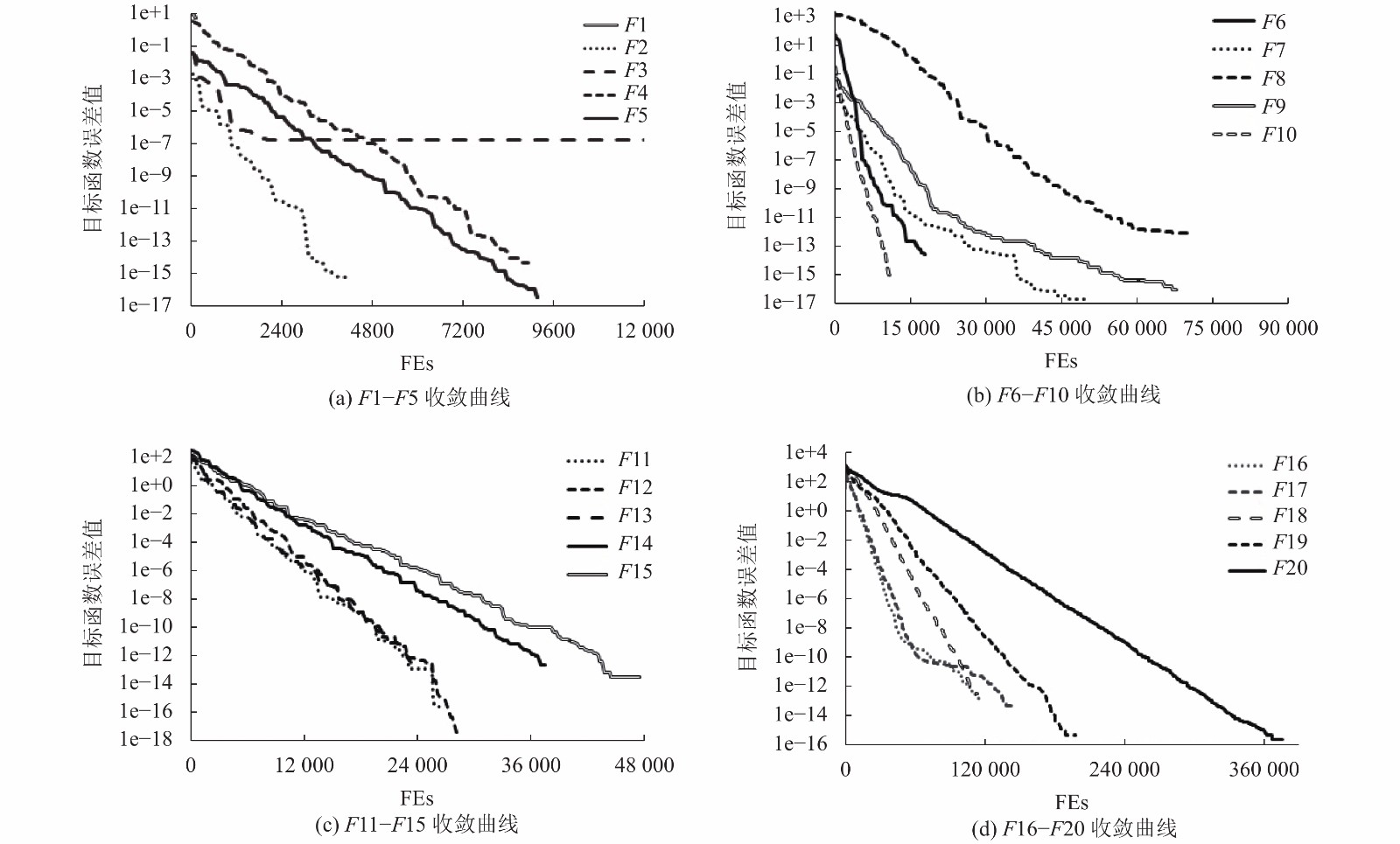
|
图 2 目标函数误差值收敛曲线 |
5 结论与展望
针对多模态优化问题, 本文提出了一种基于邻域低密度个体的差分进化算法LDPDE, 它可以通过邻域范围内个体的密度变化达到算法探索与收敛之间的平衡, 有效提升了算法的可靠性和收敛速度, 结合新提出的DE/low-density/1变异算子, 使得算法在探索阶段可以寻找尽可能多的有效个体. 在CEC2013多模态基准测试的实验结果表明, LDPDE对比其它多种基于DE的多模态优化算法具有更好的性能, 显示了LDPDE在求解多模态优化问题上的优势.
| [1] |
Pham MT, Song MH, Koh CS. Coupling particles swarm optimization for multimodal electromagnetic problems. Journal of Electrical Engineering & Technology, 2010, 5(3): 423-430. DOI:10.5370/JEET.2010.5.3.423 |
| [2] |
Zhao SZ, Suganthan PN. Diversity enhanced particle swarm optimizer for global optimization of multimodal problems. Proceedings of 2009 IEEE Congress on Evolutionary Computation. Trondheim, Norway. 2009. 590–597.
|
| [3] |
Kumar V, Chhabra JK, Kumar D. Variance-based harmony search algorithm for unimodal and multimodal optimization problems with application to clustering. Cybernetics and Systems, 2014, 45(6): 486-511. DOI:10.1080/01969722.2014.929349 |
| [4] |
Lapizco-Encinas G, Kingsford C, Reggia J. Particle swarm optimization for multimodal combinatorial problems and its application to protein design. Proceedings of 2010 IEEE Congress on Evolutionary Computation. Barcelona, Spain. 2010. 1–8.
|
| [5] |
De Jong K. Analysis of the behavior of a class of genetic adaptive systems[Ph.D. thesis]. Ann Arbor: University of Michigan, 1975.
|
| [6] |
Lin CY, Wu WH. Niche identification techniques in multimodal genetic search with sharing scheme. Advances in Engineering Software, 2002, 33(11–12): 779-791. DOI:10.1016/S0965-9978(02)00045-5 |
| [7] |
Yin XD, Germay N. A fast genetic algorithm with sharing scheme using cluster analysis methods in multimodal function optimization. In: Albrecht RF, Reeves CR, Steele NC, eds. Artificial Neural Nets and Genetic Algorithms. Vienna: Springer, 1993. 450–457.
|
| [8] |
Bessaou M, Pétrowski A, Siarry P. Island model cooperating with speciation for multimodal optimization. Proceedings of the 6th International Conference on Parallel Problem Solving from Nature PPSN VI. Paris, France. 2000. 437–446.
|
| [9] |
Kennedy J, Mendes R. Population structure and particle swarm performance. Proceedings of 2002 Congress on Evolutionary Computation. Honolulu, HI, USA. 2002.1671–1676.
|
| [10] |
Storn R, Price K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 |
| [11] |
Zhou XG, Zhang GJ, Hao XH, et al. A novel differential evolution algorithm using local abstract convex underestimate strategy for global optimization. Computers & Operations Research, 2016, 75: 132-149. DOI:10.1016/j.cor.2016.05.015 |
| [12] |
Wang HF, Moon I, Yang SX, et al. A memetic particle swarm optimization algorithm for multimodal optimization problems. Information Sciences, 2012, 197: 38-52. DOI:10.1016/j.ins.2012.02.016 |
| [13] |
Zhang ZH, Zhong CQ, Xu ZZ, et al. A non-dominated sorting cooperative co-evolutionary differential evolution algorithm for multi-objective layout optimization. IEEE Access, 2017, 5: 14468-14477. DOI:10.1109/ACCESS.2017.2716111 |
| [14] |
Thomsen R. Multimodal optimization using crowding-based differential evolution. Proceedings of 2004 Congress on Evolutionary Computation. Portland, OR, USA. 2004. 1382–1389.
|
| [15] |
Li XD. Efficient differential evolution using speciation for multimodal function optimization. Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation. Washington, DC, USA. 2005. 873–880.
|
| [16] |
Qu BY, Suganthan PN, Liang JJ. Differential evolution with neighborhood mutation for multimodal optimization. IEEE Transactions on Evolutionary Computation, 2012, 16(5): 601-614. DOI:10.1109/TEVC.2011.2161873 |
| [17] |
Gao WF, Yen GG, Liu SY. A cluster-based differential evolution with self-adaptive strategy for multimodal optimization. IEEE Transactions on Cybernetics, 2014, 44(8): 1314-1327. DOI:10.1109/TCYB.2013.2282491 |
| [18] |
Zhang YH, Gong YJ, Zhang HX, et al. Toward fast niching evolutionary algorithms: A locality sensitive hashing-based approach. IEEE Transactions on Evolutionary Computation, 2017, 21(3): 347-362. DOI:10.1109/TEVC.2016.2604362 |
| [19] |
邓然然, 李伟, 杨荣新. 自调节步长果蝇优化的自适应密度峰值聚类. 计算机系统应用, 2020, 29(4): 126-136. DOI:10.15888/j.cnki.csa.007343 |
| [20] |
Rodriguez A, Laio A. Clustering by fast search and find of density peaks. Science, 2014, 344(6191): 1492-1496. DOI:10.1126/science.1242072 |
| [21] |
Wang SL, Wang DK, Li CY, et al. Comment on “clustering by fast search and find of density peaks”. arXiv: 1501.04267, 2015.
|
| [22] |
Biswas S, Kundu S, Das S. Inducing niching behavior in differential evolution through local information sharing. IEEE Transactions on Evolutionary Computation, 2015, 19(2): 246-263. DOI:10.1109/TEVC.2014.2313659 |
| [23] |
Biswas S, Kundu S, Das S. An improved parent-centric mutation with normalized neighborhoods for inducing niching behavior in differential evolution. IEEE Transactions on Cybernetics, 2014, 44(10): 1726-1737. DOI:10.1109/TCYB.2013.2292971 |
| [24] |
Wang ZJ, Zhan ZH, Zhang J. Distributed minimum spanning tree differential evolution for multimodal optimization problems. Soft Computing, 2019, 23(24): 13339-13349. DOI:10.1007/s00500-019-03875-x |
| [25] |
Otani T, Suzuki R, Arita T. DE/isolated/1: A new mutation operator for multimodal optimization with differential evolution. Proceedings of the 24th International Conference on Advances in Artificial Intelligence. Perth, Australia. 2013. 99–105.
|
| [26] |
Li XD, Engelbrecht A, Epitropakis MG. Benchmark functions for CEC’2013 special session and competition on niching methods for multimodal function optimization [Technical Report]. Australia: Evolutionary Computation and Machine Learning Group, RMIT University, 2013.
|
 2021, Vol. 30
2021, Vol. 30



