目前我国的空气污染日趋严峻, 众多地区频繁出现了雾霾天气[1], 对人们的健康和生产活动的危害日趋显著. 因空气污染导致过早死亡的人数不断增加, 已经成为造成中国居民死亡的第四大死因[2]. 严重雾霾天气导致高速关闭, 航班停飞, 影响人们日常生产活动的进行[3]. 由于空气质量指数(Air Quality Index, AQI)的评价标准更符合人们对空气质量的真实感受, 且治理空气污染需要长时间的控制才能得到显著效果, 因此对空气质量指数进行有效的预测, 能短时间内减少对人们健康的危害和促进社会的稳定, 具有重大的现实意义.
目前国内外主要采用机器学习的方法对空气质量进行预测, 如Bai等利用小波分析将污染物历史时间序列分解成不同尺度, 结合BP神经网络模型对每日空气污染物的浓度进行预测, 结果表明该模型的预测性能优于mono-BPNN模型[4]. Wang等提出一种结合了两阶段分解技术和通过差分算法优化的极限学习机的混合预测模型, 对中国北京和上海的每日AQI数据进行实证研究, 实证结果表明该混合模型的预测精度更高[5]. 刘笃晋等利用改进的人工蜂群算法优化神经网络的权值和阈值, 在空气质量预测中有很好的应用[6]. 常恬君等建立了Prophet-随机森林优化模型, 对上海市空气质量进行分析预测, 预测结果表明该模型的预测精度更高[7].
目前很少有研究关注空气质量指数预测模型的预测性能受离群点影响较大的问题, 并且任何预测模型都存在误差, 大多数研究忽视了误差修正能提高模型的预测精度. 因此, 本文首先利用孤立森林算法对空气质量数据进行离群点分析, 然后选取对离群点泛化性能较强的离群鲁棒极限学习机模型(ORELM)对空气质量指数进行预测, 最后构建误差修正模块进一步提高模型的预测性能.
1 空气质量指数预测模型研究本文对空气质量指数的预测研究, 首先利用孤立森林算法验证实验数据中是否存在离群点, 然后采用随机森林算法筛选出最优因素子集作为预测模型的输入变量, 最后构建离群鲁棒极限学习机预测模型对AQI指数进行预测, 模型相关理论介绍如下.
1.1 基于孤立森林的离群点检测离群点指在一个时间序列中远离一般水平的极端大值和极端小值. 由于常常会出现某日空气质量特别好或特别差的情况, 则AQI值极小或极大, 因此空气质量指数数据中一般会存在离群点. 为验证本文的空气质量数据中是否存在离群点, 采用孤立森林算法对其进行分析.
孤立森林(isolation Forest, iForest)是一种无监督学习算法, 最早由莫纳什大学的Liu FT、Ting KM和南京大学的周志华提出[8]. 在孤立森林中, 异常值的定义为分布稀疏且离密度高的群体较远的点[9]. 孤立森林的基本思想是采用一个随机超平面对数据集空间进行切割, 切割一次产生两个子空间, 然后继续采用一个随机超平面对两个子空间进行切割, 一直循环下去, 直到每个子空间只剩下一个数据点[10]. 由于异常值处于密度较低的区域, 很早就能停止切割, 正常的数据处于密度较高的区域, 需要进行很多次切割才能停止.
孤立森林算法是一种集成学习算法, 由多颗孤立树(isolation Tree, iTree)组成, 每棵孤立树都具有二叉树结构[11]. 其构建一颗孤立树的步骤如下:
(1)从数据集中均匀抽取Ψ个样本作为孤立树的训练样本.
(2)在训练样本中, 随机选择一个样本特征, 并在该样本特征的最小值和最大值范围内随机选择一个值P作为孤立树的根节点.
(3)对样本进行切割, 将小于P的样本值划分到根节点的左边, 大于P值的样本点划分到根节点的右边.
(4)对切割产生的左右两个数据集重复步骤(2)和步骤(3)操作, 直到节点只有一个数据或者达到最大限度树的高度.
重复上述的操作构建N棵孤立树,利用测试数据对孤立森林进行训练, 使每一个样本点遍历所有孤立树, 直到达到终止条件, 计算样本点经过的路径长度[12]. 在这种随机分割策略下, 异常点的路径通常都较短, 最先被分割出来.
1.2 随机森林算法筛选最优因素子集空气质量指数的影响因子较多, 利用随机森林对影响因子进行重要性度量, 筛选出最优因素子集作为预测模型的输入变量, 可以减少冗余因子对预测结果的影响.
随机森林算法是由Breiman等提出, 其变量重要性度量可以作为分析特征选择的工具, 且具有很好的鲁棒性[13,14].
随机森林进行特征选择的主要思想是向一个重要特征中加入噪声时, 预测的准确率会降低, 若是无关特征则预测准确率变化不大. 具体利用袋外数据计算随机森林中的每个决策树的袋外数据误差, 记原始袋外数据误差为
| $MDA=\sum{{}{\left( errOO{{B}_{1}}-errOO{{B}_{2}} \right)}/{}{{{N}_{\rm tree}}}\;}$ | (1) |
若袋外误差准确率降低幅度越大, 则该特征对该样本的影响越大. 利用随机森林算法分析特征重要性的具体步骤如下:
(1)利用Bootstrap重采样方法, 从原始数据集中随机产生K个训练集, 构成K棵决策树[15];
(2)从m个特征中随机选取n个特征作为分裂属性集, 并从该属性集中选择最好的分裂方式对该节点进行分裂;
(3)每棵树都完整生长, 不进行任何修剪;
(4)将生成的多颗决策树组成随机森林, 利用投票的方法得到分类结果;
(5)利用袋外数据误差计算每个特征的重要性, 并对特征进行降序排序;
(6)确定一个删除比例, 将相应比例不重要的特征从当前特征变量中剔除, 从而得到一个新的特征集;
(7)新的随机森林由上一步得到的新的特征子集来构建, 计算特征集中每个特征的重要性, 并进行排序;
(8)重复步骤(5)–(7), 直到剩下n个特征;
(9)计算以上生成的每个特征集和相应建立的随机森林的袋外数据误差, 选择误差最低的特征子集.
1.3 离群鲁棒极限学习机预测模型极限学习机(Extreme Learning Machine, ELM)是一种特殊的单隐含层前馈神经网络, 其在训练过程中随机生成输入层与隐含层间的权值以及隐含层的阈值, 并且在整个训练过程中, 权值和阈值都保持不变, 只需要预先设置隐含层神经元数, 就能得到预测结果[16]. 因此该算法结构简单, 训练速度快. 模型表达式可简化为:
| $ H\beta = Y $ | (2) |
| $\begin{array}{l} H\left( {{w_1},{w_2},\cdots,{w_l},{b_1},{b_2},\cdots,{b_l},{x_1},{x_2},\cdots,{x_Q}} \right)\\ =\left[\!\!\! {\begin{array}{*{20}{c}} {g({w_1} \cdot {x_1} + {b_1})}&{g({w_2} \cdot {x_1} + {b_2})}& \cdots &{g({w_l} \cdot {x_1} + {b_L})}\\ \vdots & \vdots &{}& \vdots \\ {g({w_1} \cdot {x_Q} + {b_1})}&{g({w_2} \cdot {x_Q} + {b_2})}& \cdots &{g({w_l} \cdot {x_Q} + {b_L})} \end{array}} \!\!\!\right] \end{array} $ | (3) |
| $\beta = [\begin{array}{*{20}{c}} {{\beta _1}}&{{\beta _2}}&{ \cdots }&{{\beta _L}]{}^{\rm{T}}} \end{array}$ | (4) |
| $Y = \left[ {\begin{array}{*{20}{c}} {{y_1}}&{{y_2}}&{ \cdots }&{{y_Q}} \end{array}} \right]_{m \times Q}^{\rm{T}}$ | (5) |
其中, H为模型网络结构隐含层的输出,
| $\beta = {H^ + }Y$ | (6) |
其中, H+是隐含层的输出矩阵H的Moore-Penrose广义逆.
由于最小二乘法分配给每个输入数据相同的权重, 因此当输入数据集中存在离群点时, 这些离群点的影响会被放大, ELM模型的预测性能会降低[17]. 为了解决离群值对模型预测性能的影响, Zhang和Luo[18]提出了离群鲁棒极限学习机(Outlier Robust Extreme Learning Machine, ORELM). ORELM模型为了不失去稀疏性且能达到最小化凸, 其目标函数变成一个约束凸优化问题[19], 表达式为:
| $\left\{ {\begin{array}{*{20}{l}} {\min \limits_{\beta}{{\left\| e \right\|}_1} + \dfrac{1}{c}\left\| \beta \right\|_2^2} \\ {e = y - H\beta } \end{array}} \right.$ | (7) |
该约束凸优化问题可以由拉格朗日乘数(Augmented Lagrange Multiplier, ALM)方法来求解, 表达式为:
| ${L_\mu }\left( {e,\beta ,\lambda } \right) = {\left\| e \right\|_1} + \frac{1}{c}\left\| \beta \right\|_2^2 + {\lambda ^{\rm{T}}}\left( {y - H\beta - e} \right) + \frac{\mu }{2}\left\| {y - H\beta - e} \right\|_2^2$ | (8) |
拉格朗日函数可以通过增广拉格朗日乘子来求解, 新的迭代方式为:
| $\left\{ {\begin{array}{*{20}{l}} {{\beta _{k + 1}} = {\arg\min \limits_{\beta} }{L_\mu }({e_t},\beta ,{\lambda _k})} \\ {{e_{k + 1}} = {\arg\min \limits_{e} }{L_\mu }({e_t},{\beta _{k + 1}},{\lambda _k})} \\ {{\lambda _{k + 1}} = {\lambda _k} + \mu (y - H{\beta _{k + 1}} - {e_{k + 1}})} \end{array}} \right.$ | (9) |
βk+1和ek+1通过以下公式求得:
| $\left\{ {\begin{array}{*{20}{l}} {{\beta _{k + 1}} = {{\left( {{H^{\rm{T}}}H + \dfrac{2}{{C\mu I}}} \right)}^{ - 1}}{H^{\rm{T}}}\left( {Y - {e_k} + \dfrac{{{\lambda _k}}}{\mu }} \right)} \\ {{e_{k + 1}} = shrink\left( {y - H{\beta _{k + 1}} + \dfrac{{{\lambda _k}}}{\mu },\dfrac{1}{\mu }} \right)} \end{array}} \right.$ | (10) |
不论是单一预测模型还是混合预测模型都会存在一定的误差, 可以通过一些非线性模型对原预测模型的误差进行预测, 进而修正模型的预测结果, 以达到提高模型预测性能的目的. 误差修正模块构建的关键是误差时间序列的预测及修正模型的选择. 具体步骤如下:
(1)产生误差时间序列
O(t)为t时刻的模型预测值, A(t)为在t时刻的真实值, 则模型在t时刻的预测误差值为:
| $error(t) = A(t) - O(t)$ | (11) |
(2)进行误差预测
由于误差值具有时间序列特征, 假设t时刻的误差值由前k个时刻的误差值预测得到,
| $Ef(t) = f[error(t - 1),error(t - 2),\cdots,error(t - k)]$ | (12) |
由于支持向量机模型是一种基于时间序列的回归模型, 泛化性能强, 需要调节的参数少, 本文选择支持向量机模型作为误差时间序列预测模型.
(3)进行误差修正, 得到最终预测值
得到误差序列预测值后, 大部分误差修正模型直接将原模型预测值和误差预测值相加得到最终的模型预测值, 忽略简单相加产生的问题. 本文通过建立非线性预测模型
| $F(t) = F[Ef(t),O(t)]$ | (13) |
其中, 非线性预测模型
本文选取北京市2013年12月2日到2017年2月28日共1184组AQI数据和6种污染物数据(PM2.5, PM10, NO2, SO2, CO, O3), 以及同时期风速、气压、气温、降雨量4种气象数据作为研究对象, 数据来源于中国环境监测总站和中国气象局.
3.2 离群点检测利用Python语言中的isolationForest包完成对空气质量数据集的离群点检测, 将经过预处理的空气质量指数数据作为输入数据, 使其遍历每一棵孤立树, 计算其路径长度, 结果如图1所示.
如图1所示, AQI数据中存在一定数量的离群点, 若是将这些离群点都删除, 会影响数据集的分布. 本文采用对离群点泛化性能较强的离群鲁棒极限学习机预测模型对空气质量指数进行预测来减小离群点的影响.
3.3 最优因素子集筛选利用随机森林对影响因素进行重要性排序通过R语言中的randomForest程序包来完成, 将前一天的空气污染物数据和当天的气象数据作为输入数据, 当天的AQI数据作为输出值. 其中参数设置: 决策树(Ntree)设置为100棵, importance=TRUE表示要计算变量的特征重要性, 其他参数为默认值. 因子重要性排序如图2所示, 其中日均风速的重要性最大. 依次将重要性最小的因子去掉, 将剩下因素子集输入极限学习机模型中进行预测, 以均方根误差为评价指标. 各因素子集对应的均方根误差如图3所示. 由图3中可以看出, 当不重要的因子删除时, 预测误差降低; 随着重要性高的因子删除, 误差又逐渐提高. 当因子数量为8个时, 均方根误差达到最低. 最终筛选出来的最优特征子集为日均风速、NO2、PM10、CO、PM2.5、日均气压、日均气温及O3.

|
图 1 离群点检测结果 |

|
图 2 因素重要性排序 |

|
图 3 各因素子集相对应的均方根误差 |
3.4 预测模型实证分析
为了证明本文选择的离群鲁棒极限学习机模型在预测离群样本点上的优越性, 将其与极限学习机模型进行对比实验, 两个模型的隐含层神经元数量都设置为50. 首先对空气质量数据集进行归一化处理, 将其中的1100组数据作为训练集数据, 剩余的84组数据作为测试集数据. 根据筛选出来后的最优因素子集, 将预测日前一天的NO2、PM10、CO、PM2.5、O3数据以及预测日的日均风速、日均气压以及日均气温数据作为模型的输入数据, 预测日当天的AQI数据作为模型的输出变量. 以平均绝对百分误差(MAPE)、均方根误差(RMSE)、平均绝对误差(MAE)作为评价指标, 结果如表1所示.
| 表 1 预测结果评价表 |
由表1所示, 离群鲁棒极限学习机的3个误差值都小于极限学习机, 表明ORELM模型对存在离群点的样本数据泛化性能更强, 能有效的提高模型的预测性能.
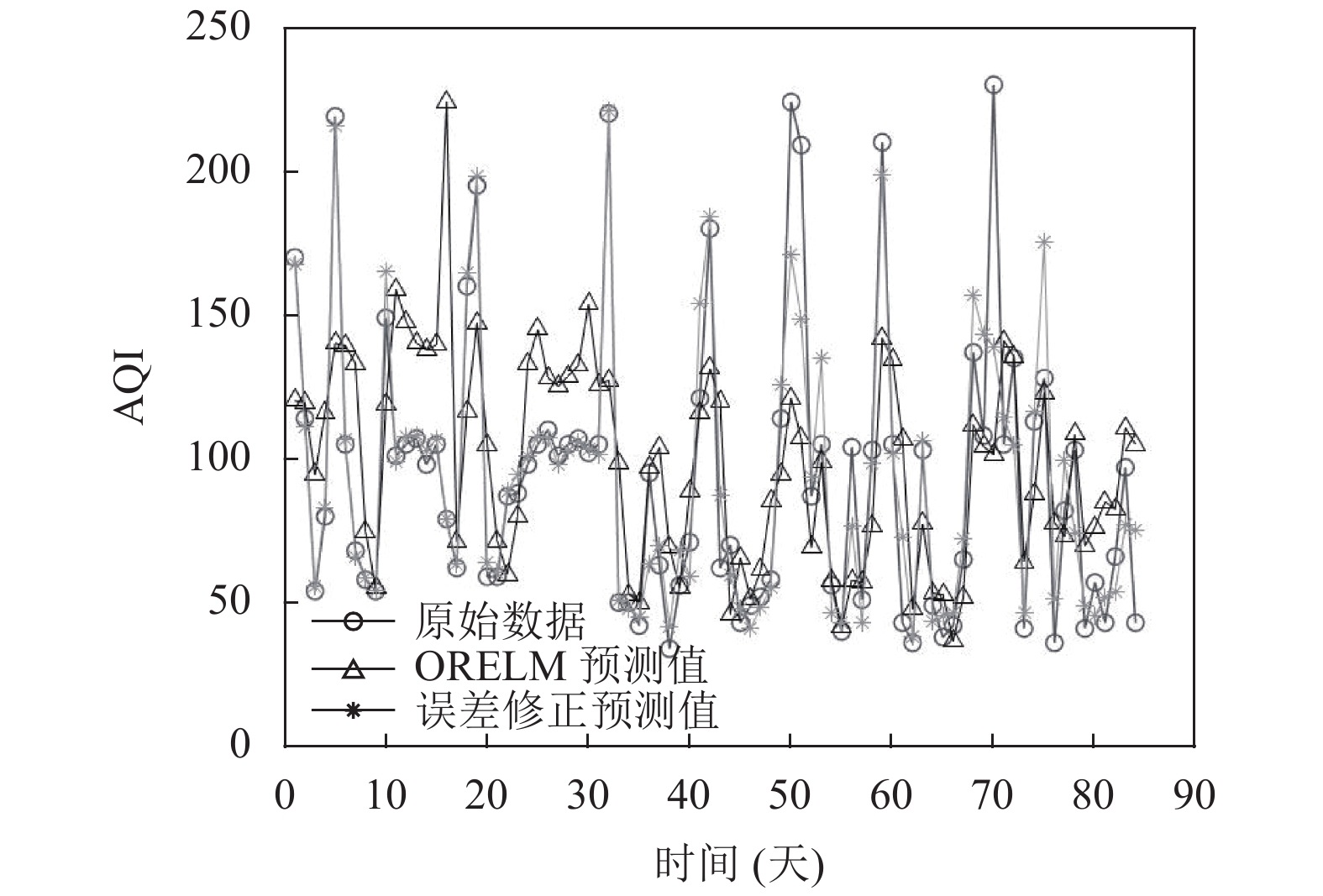
3.5 误差修正实证分析为了验证误差修正模块的有效性, 将经过误差修正后的预测结果与原模型预测结果进行比较, 预测结果对比图如图4所示. 由图4可以看出经过误差修正之后的模型拟合能力更强, 预测精度明显提高. 经误差修正后, 模型的MAPE、RMSE、MAE分别为0.1289、18.7728、11.2148, 均比原模型预测误差低, 表明误差修正模块能有效的提高模型的预测性能.
|
图 4 模型预测对比图 |
4 结论
空气污染一般需要长时间的治理才能得到显著效果, 因此, 提高空气质量指数预测模型的精度, 对人们身体健康和社会稳定具有重大的研究意义. 本文从离群点检测和误差修正两个角度来提高模型的预测性能. 利用孤立森林对空气质量数据进行离群点检测, 检测结果表明数据集中存在一定数量的离群点, 采用对离群点泛化性能更强的离群鲁棒极限学习机模型对空气质量进行预测来消除离群点的影响, 并对模型预测值进行误差修正. 根据平均绝对百分误差(MAPE)、均方根误差(RMSE)、平均绝对误差(MAE) 3个评价指标, 得出离群鲁棒极限学习机模型对存在离群点的样本数据泛化性能更强, 经过误差修正后, 预测误差降低, 表明误差修正能有效的提高模型的预测性能. 而对于空气污染程度不同的城市, 该模型是否能对空气质量指数进行有效的预测以及更长的预测时间都是后续需要进一步研究的内容.
| [1] |
王继志, 杨元琴, 周春红, 等. 雾霾低能见度天气分析与预测方法研究. 中国气象学会会议论文集. 广州, 中国. 2007. 152–156.
|
| [2] |
Yang GH, Wang Y, Zeng YX, et al. Rapid health transition in China, 1990–2010: Findings from the Global Burden of Disease study 2010. The Lancet, 2013, 381(9882): 1987-2015. DOI:10.1016/S0140-6736(13)61097-1 |
| [3] |
谢杨, 戴瀚程, 花岡達也, 等. PM2.5污染对京津冀地区人群健康影响和经济影响. 中国人口·资源与环境, 2016, 26(11): 19-27. DOI:10.3969/j.issn.1002-2104.2016.11.003 |
| [4] |
Bai Y, Li Y, Wang XX, et al. Air pollutants concentrations forecasting using back propagation neural network based on wavelet decomposition with meteorological conditions. Atmospheric Pollution Research, 2016, 7(3): 557-566. DOI:10.1016/j.apr.2016.01.004 |
| [5] |
Wang DY, Wei S, Luo HY, et al. A novel hybrid model for air quality index forecasting based on two-phase decomposition technique and modified extreme learning machine. Science of the Total Environment, 2017, 580: 719-733. DOI:10.1016/j.scitotenv.2016.12.018 |
| [6] |
刘笃晋, 蒲国林, 王光琼. 基于蜂群优化神经网络的环境空气质量预测. 计算机与数字工程, 2018, 46(4): 639-643. DOI:10.3969/j.issn.1672-9722.2018.04.002 |
| [7] |
常恬君, 过仲阳, 徐丽丽. 基于Prophet-随机森林优化模型的空气质量指数规模预测. 环境污染与防治, 2019, 41(7): 758-761, 766. |
| [8] |
Liu FT, Ting KM, Zhou ZH. Isolation forest. Proceedings of 2008 Eighth IEEE International Conference on Data Mining. Pisa, Italy. 2008. 413–422.
|
| [9] |
李星男, 施展, 亢中苗, 等. 基于孤立森林算法和BP神经网络算法的电力运维数据清洗方法. 电器应用, 2018, 37(16): 72-79. |
| [10] |
李新鹏, 高欣, 阎博, 等. 基于孤立森林算法的电力调度流数据异常检测方法. 电网技术, 2019, 43(4): 1447-1456. |
| [11] |
陈佳, 欧阳金源, 冯安琪, 等. 边缘计算构架下基于孤立森林算法的DoS异常检测. 计算机科学, 2020, 47(2): 287-293. DOI:10.11896/jsjkx.190100047 |
| [12] |
肖伟洋. 基于孤立森林算法的空气质量数据异常检测分析. 信息与电脑, 2019, 31(17): 38-40. |
| [13] |
Breiman L. Random forests. Machine Learning, 2001, 45(1): 5-32. DOI:10.1023/A:1010933404324 |
| [14] |
姚登举, 杨静, 詹晓娟. 基于随机森林的特征选择算法. 吉林大学学报(工学版), 2014, 44(1): 137-141. |
| [15] |
林开春, 邵峰晶. 基于随机森林和神经网络的空气质量预测研究. 青岛大学学报(工程技术版), 2018, 33(2): 32-36. |
| [16] |
王小川, 史峰, 郁磊, 等. MATLAB神经网络43个案例分析. 北京: 北京航空航天大学出版社, 2013. 243–255.
|
| [17] |
胡义函, 张小刚, 陈华, 等. 一种基于鲁棒估计的极限学习机方法. 计算机应用研究, 2012, 29(8): 2926-2930. DOI:10.3969/j.issn.1001-3695.2012.08.033 |
| [18] |
Zhang K, Luo MX. Outlier-robust extreme learning machine for regression problems. Neurocomputing, 2015, 151: 1519-1527. DOI:10.1016/j.neucom.2014.09.022 |
| [19] |
王建州, 杨文栋. 基于非线性修正策略的空气质量预警系统研究. 系统工程理论与实践, 2019, 39(8): 2138-2151. DOI:10.12011/1000-6788-2018-2470-14 |
 2021, Vol. 30
2021, Vol. 30



