1 引言

近几年来, 生成对抗网络(Generative Adversarial Network, GAN)在计算机视觉、图像处理等多个领域得到越来越多的应用. 其中包括应用最广泛的图像到图像的转换, 它可以将来自不同域的图像进行相互之间转换. 场景图像转换可以看成是图形处理和计算机视觉领域相结合的问题. 传统的场景图像转换算法大多是基于模型的方法. 孙毅刚等^[1]提出一种基于改进的snake模型, 该算法利用模糊连接度准确找到雨雪轮廓点, 并通过模糊相似度函数确定雨雪边界, 实现雨雪场景图像转换. 刘杰平等^[2]基于大气散射模型, 提出了一种适应人眼视觉特征的HSI色彩空间估计大气光和透射率, 实现雾霾场景图像转换. 费子豪等^[3]建立了基于高频分量直方图均衡化, 低频分量同态滤波处理的小波变换模型, 完成晴天多云场景图像转换.

场景图像转换是图像转换的一类问题. 解决图像转换问题大多使用基于学习的方法, 利用卷积神经网络的强大特征表示能力, 学习源域到目标域图像的映射函数. 为了学习到这个映射函数, 许多国内外学者展开了广泛的科学研究. 得益于文献[4], 其将生成对抗网络(GAN)引入到深度学习领域, 给生成图像工作带来了更加新颖的方法. 基于GAN网络模型, 提出各种改进的图像转换模型. Mirza等^[5]提出了带条件约束的cGAN(conditional GAN)模型, 该网络模型通过添加条件变量限制生成结果. 基于cGAN的思想, Isola等^[6]提出Pix2Pix算法模型, 该算法要求配对的图像数据集, 能够无监督地学习到不同域图像之间的映射关系. Kim等^[7]提出DiscoGAN模型在跨域图像转换中发挥不错的效果. Yi等^[8]借鉴对偶学习的思想提出DualGAN. Radford等^[9]提出DCGAN, 极大的提高了图像生成的实用性. Zhu等^[10]提出了CycleGAN网络, 该方法突破了要求成对图像数据集的限制, 无需配对数据集就能够实现不同域图像之间的转换工作.

本文正是基于CycleGAN网络, 提出了一种场景图像转换的新方法. 通过改进的生成网络结构、SSIM结构重建损失和身份保持损失, 应用到场景图像转换上能够取得很好的效果.

2 相关工作 2.1 生成对抗网络(GAN)

生成对抗网络(GAN)是一个十分强大的生成模型, 它能够在各种不同的计算机视觉任务中取得优秀的结果. GAN基于连续数据, 且假设有无限建模能力^[11]. 其灵感来源于零和博弈思想, 通过双方的博弈过程, 达到两者之间纳什平衡. 其由两种网络结构模型组成: 生成网络G (Generator)和判别网络D (Discriminator). 判别网络D用来判断样本图像是原始图像还是由生成网络G生成的图像, 目的是将他们区分开来. 而生成网络G则尽可能的生成更加逼真的图像, 以此来迷惑判别网络D, 达到以假乱真的目的. 通过G和D之间相互对抗, 直到生成的图像判别网络无法分辨.

GAN的优化目标函数为:

$ \begin{split} \mathop {\min }\limits_G \mathop {\max }\limits_D V(G,D) =& {{{E}}_{x\sim {p_{\rm data}}(x)}}\left[ {\log D(x)} \right] \\ &+{{{E}}_{{\textit{z}}\sim {p_{\textit{z}}}({\textit{z}})}}\left[ {\log (1 - D(G({\textit{z}})))} \right] \end{split} $

(1)

其中, x表示真实图片, 采样于真实数据分布, ${\textit{z}}$ 表示输入生成网络G的随机噪声, 采样于正态分布. $D(x)$ 表示输入的图片x接近真实图片的概率. 训练是批量进行的, E为数学期望. D希望 $D(x)$ 变大, $D(G({\textit{z}}))$ 变小, 所以D尽可能的最大化目标函数. G希望 $D(G({\textit{z}}))$ 变大, 这时G尽可能的最小化目标函数.

2.2 CycleGAN模型

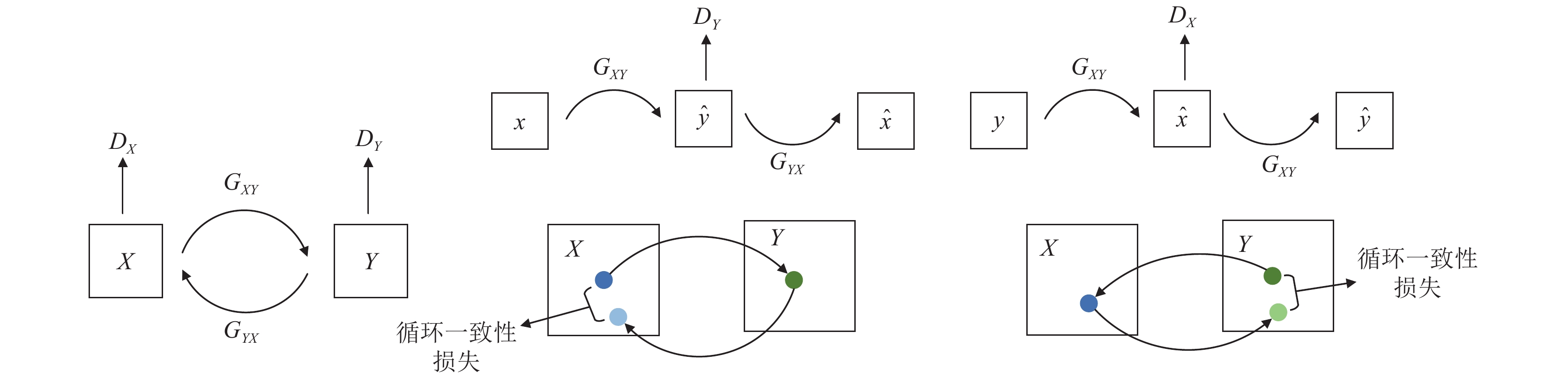
CycleGAN模型工作在无配对的数据集上, 实现跨域图像转换. 其网络结构由两个生成网络 ${G_{XY}}$ 、 ${G_{YX}}$ 和两个判别网络 ${D_X}$ 、 ${D_Y}$ 组成. G与D相互对抗过程类似于一种双向环结构. 其整体结构如图1所示.

图1中, 左边部分是 ${G_{XY}}$ 与 ${D_Y}$ , ${G_{YX}}$ 与 ${D_X}$ 之间的对抗. 中间部分是将X域中的图像经过两次转换回原域后反馈调节网络参数, 右边部分与之类似, 作用于Y域中的图像.

该模型的目标函数由两部分损失函数组成, 对抗损失和循环一致损失. 对抗损失表示生成网络和判别网络之间的对抗, 生成网络尽可能生成接近真实样本分布的图像, 而判别网络尽可能将他们分辨出来. 通过网络之间的对抗, 模型可以学习到很好的映射函数 ${G_{XY}}$ 和 ${G_{YX}}$ , 然而单靠对抗损失还不能够保证学习函数能够将单个输入 ${x_i}$ 映射到期望的输出 ${y_i}$ , 因此需要循环一致损失缩小映射函数空间. 循环一致损失类似于对偶学习, 它通过前后两次转换将输入x映射回原始域, 例如 $x \to {G_{XY}}(x) \to {G_{YX}}({G_{XY}}(x)) \approx x$ , 然后根据反馈回来的信息就能指导模型优化改进.

2.3 跳跃连接和残差块

跳跃连接(skip connections)^[12]常用在生成网络结构中, 以保证图像空间位置信息在网络传递中的连续性. 通常生成网络包含下采样部分和上采样部分, 在下采样中, 输入是原始图像, 每经过一次下采样, 图像都会在空间上被压缩, 同时扩张图像的通道数. 相反, 上采样中, 图像在空间上拓展, 相应的通道数减少. 这样的网络是线性的, 图像数据从输入层流入, 通过网络一层接一层的向下流动, 最后到达输出层.

在下采样部分的网络中, 经过每一个连续的层, 模型都会提取到图像特征内容, 但却丢失了图像空间位置信息. 在下采样的最后一层, 特征图已经有足够强的能力学习到图像的内容, 但几乎不理解空间位置. 对于预测分类问题, 这已经足够了, 所以我们可以把它连接到一个稠密层上, 来输出一个特定类出现在图像中的概率. 然而, 对于图像生成或者图像转换问题, 需要在上采样回到原始图像大小过程中将下采样丢失的空间位置信息传递回每一层. 这就是需要跳跃连接, 它允许网络将在下采样过程中捕获的高级抽象信息与从网络的先前层反馈来的特定空间信息进行混合.

为了让网络提取到的特征更加丰富, 避免在非采样层中, 过深的网络进行卷积和池化操作时导致的图像信息丢失, 我们也引入了残差块(residual block)^[13]. 其结构如图2所示.

残差块通过跳跃连接将浅层特征直接传递到深层特征, 其工作方式是将输入与残差块的网络输出叠加后作为最后的输出. 通过跳跃连接将图像特征向神经网络的更深层传递, 即使网络结构更深, 也不会出现特征丢失的现象. 同时还有效的解决了梯度消失和梯度爆炸问题, 提高了网络的稳定性.

3 改进的网络模型

本文从网络结构和损失函数两个方面改进网络模型.

3.1 判别网络结构

本文设计了一个全卷积多层下采样网络结构, 通过提取场景图像特征, 将真假图像辨别出来. 所提的判别网络包含两类 ${D_X}$ 和 ${D_Y}$ , ${D_X}$ 用来判别输入的图像是否来自X域中的真实图像, ${D_Y}$ 将Y域中的真实图像y与生成的图像区分开来. 它们共用同一网络结构, 但模型参数不共享. 判别网络结构如图3所示.

网络的输入为3通道大小为的图片, 随后通过边下采样边拓展通道的方式, 提取图像内容特征. 采用步幅为2, 卷积核大小为3×3的卷积操作, 每次卷积后图像宽高都减小一半, 除了输入层和输出层外, 其他层还需要连接Instance Normalization实例归一化层以及紧跟着Leaky ReLU激活层. 最后通过一个卷积核为1的卷积操作输出形状为1×16×16的特征图, 对其求取平均值作为判别网络的输出, 也就是输入图片判别为真实图像的概率.

3.2 生成网络结构

仅用卷积层提取特征存在缺陷, 没有考虑输入图像与生成图像在纹理特征和图像结构上的联系, 造成生成的图像细节模糊. 为了弥补该缺陷, 本文改进生成网络结构, 通过引入跳跃连接, 将下采样过程中丢失的图像空间结构信息传递回上采样中, 以及在加深的网络层中加入残差块进一步抑制图像纹理特征信息在传递过程中的丢失现象.

所提的生成网络同样包含两类 ${G_{XY}}:X \to Y$ 和, ${G_{XY}}$ 生成网络将X域中图像x作为输入, 尽可能去生成接近Y域数据样本分布的图像 $\hat y$ . ${G_{YX}}$ 则是与之相反, 将Y域中的图像尽可 ${G_{YX}}:Y \to X$ 能转化为X域中图像. 它们的网络结构如图4所示.

该网络输入输出图像均为3通道大小为256×256的图片. 模型左侧为下采样结构, 采用步幅为2卷积核为5×5的卷积层, 同时紧跟其后的是实例归一化层以及Leaky ReLU层. 在这里我们参考Ulyanov等^[14]的建议, 使用实例归一化层(instance normalization), 在生成网络中使用实例归一化层比批量归一化层^[15]更能生成令人满意的结果. 总共进行3次下采样, 每次图像宽高减半, 通道数加倍, 最终到达256×32×32尺寸为止. 随后保持该尺寸经过9个残差块传递图像特征, 对应着模型底部的结构. 之后, 进行向上采样回原图像尺寸, 这部分属于模型右侧的结构, 其采用相同的步幅2、卷积核5×5的反卷积层, 以及Instance Normalization层和Leaky ReLU层, 每次上采样图像大小加倍, 通道数减半, 不同的是使用跳跃连接将下采样过程中对应大小尺寸的特征图连接过来. 最后, 将上采样的结果通过通道数为3的反卷积层连接, 输出相同尺寸的图像.

3.3 损失函数

损失函数即本文所提模型的目标函数, 它是由对抗损失、SSIM重建损失和身份保持损失3个部分组成.

3.3.1 对抗损失

在原始的GAN模型中, 网络的训练过程存在着不稳定和生成图像质量不高等问题, 针对该问题, 我们将交叉熵损失替换为最小二乘损失^[16]. 对应的生成网络 ${G_{XY}}$ 和判别网络 ${D_Y}$ 的对抗损失定义如下:

$ \begin{split} {L_{\rm gan}}({G_{XY}},{D_Y}) = &\frac{1}{2}{{{E}}_{y\sim {p_{\rm data}}(y)}}\left[ {{{\left( {{D_Y}(y) - 1} \right)}^2}} \right] \\ &+\dfrac{1}{2}{{{E}}_{x\sim {p_{\rm data}}(x)}}\left[ {{{({D_Y}({G_{XY}}(x)))}^2}} \right] \end{split} $

(2)

式中, $y \sim {p_{\rm data}}(y)$ 表示变量y采样于Y域空间服从的概率分布, $x \sim {p_{\rm data}}(x)$ 表示变量x采样于X域空间服从的概率分布, ${{E}}\left[ {} \right]$ 表示计算数学期望值. 对于生成网络 ${G_{XY}}$ , 其目标是尽可能最大化 ${L_{\rm gan}}({G_{XY}},{D_Y})$ , 即生成更接近目标域 $Y$ 数据分布的图像来混淆判别网络 ${D_Y}$ 的决策. 而判别网络 ${D_Y}$ 则尽可能最小化目标, 将真实样本y和生成样本 $\hat y$ 区分开.

$ {G_{XY}}^*,{D_Y}^* = \arg \mathop {\min }\limits_{{D_Y}} \mathop {\max }\limits_{{G_{XY}}} {L_{\rm gan}}({G_{XY}},{D_Y}) $

(3)

如式(3)所示, 通过两者对抗最终达到最优解 ${G_{XY}}^*$ 和 ${D_Y}^*$ .

同样的, 对于生成网络 ${G_{YX}}$ 和判别网络 ${D_X}$ 的对抗损失定义如式(4), 通过两者之间的对抗过程寻找到最优解 ${G_{YX}}^*,{D_X}^*$ , 如式(5)所示.

$ \begin{split} {L_{\rm gan}}({G_{YX}},{D_X}) = &\frac{1}{2}{{{E}}_{x\sim {p_{\rm data}}(x)}}\left[ {{{\left( {{D_X}(x) - 1} \right)}^2}} \right]\\ &+\frac{1}{2}{{{E}}_{y\sim {p_{\rm data}}(y)}}\left[ {{{({D_X}({G_{YX}}(y)))}^2}} \right] \end{split} $

(4)

$ {G_{YX}}^*,{D_X}^* = \arg \mathop {\min }\limits_{{D_X}} \mathop {\max }\limits_{{G_{YX}}} {L_{\rm gan}}({G_{YX}},{D_X}) $

(5)

3.3.2 SSIM重建损失

通过优化上述对抗损失函数可以学习到很好的映射函数 ${G_{XY}}^*$ 和 ${G_{YX}}^*$ , 产生接近目标域空间分布的样本. 但如果有足够大的样本容量, 生成网络可以将同一组输入图像映射到目标域中任意随机排列的图像, 对于 ${G_{XY}}^*$ 生成网络, 它完全可以将所有的X域图像都映射到目标Y域的同一图像上, 从而导致对抗损失失效. 因此, 本文引入了重建损失来帮助网络进一步缩小无效的映射函数空间, 确保映射函数能够将单个输入映射到期望的输出.

同时, 为进一步保证生成图像过程中结构特性不丢失, 引入Wang等^[17]提出的结构相似性指数(Structural Similarity Index Measurement, SSIM)来衡量两幅图像的结构差异.

对于给定的图像x和y, 其结构相似性指数定义如下:

$SSIM(x,y) = \frac{{(2{\mu _x}{\mu _y} + {c_1})(2{\sigma _{xy}} + {c_2})}}{{\left( {\mu _x^2 + \mu _y^2 + {c_1})(\sigma _x^2 + \sigma _y^2 + {c_2}} \right)}} $

(6)

$ {c_1} = {({k_1}L)^2},{c_2} = {({k_2}L)^2} $

(7)

式中, ${u_x}$ 是图像x的均值, $\sigma _x^2$ 是图像x的方差, ${\sigma _{xy}}$ 是图像x和y的协方差. ${c_1}$ 与 ${c_2}$ 为两个常数, 避免除零, L为像素范围, ${k_1} = 0.01,{k_2} = 0.03$ 为默认值. SSIM结构相似性范围为−1到1, 值越大表示图像x和y越相似.

因此, 我们引入SSIM重建损失, 如式(8)所示, 模型尽可能的最小化该目标.

$ \begin{split} &{L_{\rm ssim + rec}}({G_{XY}},{G_{YX}})\\ =&{{{E}}_{x\sim {p_{\rm data}}(x)}}\left[ {1 - S\!S\!I\!M(x,{G_{YX}}({G_{XY}}(x)))} \right]\\ &+ {{{E}}_{y\sim {p_{\rm data}}(y)}}\left[ {1 - S\!S\!I\!M(y,{G_{XY}}({G_{YX}}(y)))} \right] \end{split} $

(8)

3.3.3 身份保持损失

为了让生成网络将其目标域的图像作为输入后保持不变性, 我们引入了身份保持损失. 存在这样一种情况, 将Y域中的图像y输入到 ${G_{XY}}$ 中, 满意的结果应该是图像y原封不动的从生成网络中输出. 身份保持损失能够帮助我们做到这一点, 该项损失帮助调节生成网络, 以确保它只调整完成转换所需的图像部分, 而不是更多的内容. 在保持图像内容前后一致性的同时, 也间接地维持了图像的色彩饱和度. 身份保持损失公式如式(9)所示.

$ \begin{split} {L_{id}}({G_{XY}},{G_{YX}}) = &{{{E}}_{y \sim {p_{\rm data}}(y)}}\left[ {{{\left\| {{G_{XY}}(y) - y} \right\|}_1}} \right]\\ &+{{{E}}_{x \sim {p_{\rm data}}(x)}}\left[ {{{\left\| {{G_{YX}}(x) - x} \right\|}_1}} \right] \end{split} $

(9)

模型通过最小化目标函数 ${L_{id}}({G_{XY}},{G_{YX}})$ , 保证转换图像前后内容的一致性, 同时也避免转换后的图像出现色彩失真现象, 以保留更多的色彩细节.

综合以上三项损失函数, 得到最终的目标函数为 $L({G_{XY}},{G_{YX}},{D_X},{D_Y})$ . 如式(10)所示.

$ \begin{split} &L({G_{XY}},{G_{YX}},{D_X},{D_Y})\\ =& {L_{\rm gan}}({G_{XY}},{D_Y}) + {L_{\rm gan}}({G_{YX}},{D_X})\\ &+ {\lambda _1}{L_{\rm ssim + rec}}({G_{XY}},{G_{YX}}) + {\lambda _2}{L_{id}}({G_{XY}},{G_{YX}}) \end{split} $

(10)

其中, ${\lambda _1}$ 和 ${\lambda _2}$ 分别控制3项损失之间的相对重要性.

4 实验结果与分析 4.1 实验环境和数据集

本文算法进行实验的平台环境及配置如表1所示. 选用Tensorflow作为深度学习框架, 在GPU上使用CUDNN加速训练模型, 使用的编程语言为Python.

数据集包括4个类别的场景图像, 两类季节场景summer、winter和两类天气场景cloudy、sunny. 数据分别选自MWD (Multi-class Weather Dataset)数据集、Two-class Weather Classification数据集, 组成我们需要的两类场景转换数据集, 数据集一为多云与晴天场景转换数据集(cloudy2sunny), 数据集二为夏季与冬季场景转换数据集(summer2winter). 每个数据集中每类场景各自包含训练数据5000张图片, 测试数据1000张图片, 图片大小都为256×256.

4.2 训练过程及参数设置

基于TensorFlow深度学习框架, 使用GPU加速, 采用迭代交替的方式对本文算法模型进行训练. 优化算法使用Adam, 批量大小为1, ${\lambda _1}$ 、 ${\lambda _2}$ 分别取10和5, 所有的网络从学习率为0.0002开始训练, 前100个epochs保持0.0002的学习率不变, 后100个epochs中学习率线性衰减为0, 交替迭代训练生成网络和判别网络. 模型参数如表2所示.

4.3 对比实验验证

为验证所提模型的有效性, 分别进行两类场景图像转换对比实验. 第一类场景为天气场景图像转换(多云与晴天互转), 首先分别选取不同域的图片, 输入到对应的生成网络中, 得到转换后的图像结果. 然后将实验结果与GAN、Pix2Pix、CycleGAN模型得到的结果进行定性和定量对比. 第二类场景为季节场景图像转换(夏季与冬季互转), 验证过程与上述类似.

(1)定性对比实验

使用数据集一(cloudy2sunny)训练本文所提模型. 分别选取多云图片和晴天图片各一张进行对比实验, 得到如图5所示结果. 从实验结果中可以发现, GAN模型转换后的晴天和多云场景图像模糊不清. Pix2Pix模型生成的目标场景图像部分存在结构上的缺陷问题. CycleGAN模型转换后的场景图像容易造成图像色彩失真, 与真实的图像存在差异. 本文算法生成的目标场景图像(多云和晴天)更加的接近真实场景图像.

使用数据集二(summer2winter)时, 同样选取夏季和冬季图片各一张, 将实验结果图与GAN、Pix2Pix、CycleGAN模型得到的结果进行对比, 如图6所示. 通过对比可以看出, 所提模型转换后的结果更加接近目标真实场景, 同时保持了完整的图像结构和纹理细节信息. 通过这两类场景图像转换的对比实验, 验证了本文所提模型应用到场景图像转换上的有效性和可行性.

(2)定量对比实验

定量对比部分, 我们采用广泛使用的PSNR^[18]和SSIM这两种全参考的图像质量评价指标, 来对生成的图像进行客观的定量评判. 在同一测试数据集上, 使用这两种评价指标, 将本文算法和其他算法生成的图像与真实图像进行定量对比. 各算法的评价指标结果如表3所示.

5 结束语

本文设计了基于改进生成对抗网络的图像转换算法, 应用在天气和季节场景的图像转换上能够获得很好的效果. 具体改进方法涉及以下几个方面: 首先是改进生成网络的网络结构, 通过在网络的下采样部分和上采样部分中间加入跳跃连接, 保证下采样部分的图像空间位置信息传递的连续性, 以及在非采样部分使用残差块, 保证层数加深的网络不丢失图像内容信息. 其次, 选用SSIM相似性指数作为衡量图像结构差异的指标, 组成SSIM结构重建损失, 目的是使得模型生成的图像结构更完整. 此外, 还通过添加身份保持损失, 保证转换前后图像色彩不失真和内容的一致性. 在今后的研究工作中, 我们将考虑进一步优化网络结构和损失函数, 在纹理、细节等方面, 增强原图和转换图之间的结构相似性和语义一致性.