1 引言

近年来随着科学技术的不断发展, 各种传感器, 电子元器件的体积进一步减小, 精度进一步提高, 而这些传感器和电子技术的快速发展又进一步推动环境监测从区域化粗粒度监测向更细粒度的区域网格化监测发展. 同时网格化监测手段与大数据技术的有机结合, 又使得环境监测部门可以获得更多尺度、更加详细的空气污染信息, 通过分析这些空气污染数据不但可以迅速的发现污染源头, 快速治理, 还可以对网格化监测区域内未来的空气污染状况进行预测, 因此挖掘空气污染数据的潜在信息对于推动我国生态文明建设, 改善空气质量污染状况, 提升人民生活的幸福度具有一定的意义.

长期以来, 空气质量的预测一直是国内外空气污染监测与治理相关领域的研究热点之一. 按照研究手段分类, 空气质量预测可以分为统计预测、数值预测和以机器学习为代表的人工智能算法预测这3种方案^[1], 其中统计预测是指通过分析空气中污染物的变化规律来进行预测, 常用的模型有灰度模型和回归模型. 但是单一的灰度模型或者回归模型又各自存在一些缺陷, 有的学者提出了将基于残差修正的灰度模型^[2]应用到空气质量预测的工作上面, 有效的提高了灰度模型的预测精度. 也有学者将多元线性回归模型应用到空气质量分析中, 都取得了一定的成果^[3].

有关于空气质量的数值预测是指以大气运动规律为基础, 综合空气中污染物之间可能发生的物理和化学变化, 利用数学的方法建立起污染物在空气中扩散模型来预测未来一段时间内污染物浓度的变化, 其中主流的模型有CQMA, NAQPMS, CAMs等. 虽然数值预报在空气质量预测方面有着不可取代的作用, 但是由于数值预报本身的不确定性, 所以可能会导致单一的数值预报模式的预测精准度存在问题, 所以来自浙江理工大学的谢磊提出了一种综合多种数值预报模式的空气质量的预测方法, 在一定程度上提高了空气质量的数值预测的精度^[4].

近年来随着人工智能学科的快速发展, 已经有越来越多的人将有关于机器学习, 神经网络等方面的相关知识应用到空气中污染物预测和空气质量预测方面. 有学者将支持向量机的方法与空气质量的预测相结合, 提出了基于改进萤火虫寻优支持向量机的预测模型(IFA-SVM), 该模型改进了以往使用的萤火虫算法-支持向量机(FA-SVM)在训练模型时收敛速度慢和参数震荡等问题^[5]. 有国外学者将ANN应用到空气质量预测方面并取得了较高质量的预测效果^[6], 也有学者将BP神经网络应用到空气中污染物浓度的预测工作方面, 并且使用K近邻算法(KNN)来优化传统BP神经网络方法不能体现历史时间窗内的数据对当前预测影响的问题^[7]. 还有学者将能够高效的提取连续时间特征的长短期记忆神经网络(Long Short-Term Memory, LSTM)应用到空气中污染物的浓度预测方面. 来自西安电子科技大学的张晗提出了一种基于LSTM的空气污染物预测模型, 可以有效的提取有关空气污染物浓度的历史数据之间的时间特征从而获得一个准确率较高的预测数据^[8]. 还有学者将经济因素的影响添加到空气质量的预测中, 并取得一定的成果^[9].

当前对于空气中污染物浓度预测的相关研究大多是以可以产生大量, 多元监测数据的大中型监测站为研究对象, 而以网格化监测中小微型监测站作为研究对象的研究较少. 同时, 由大中型监测站所产生的空气质量数据与网格化监测中小, 微型监测站所产生的空气质量数据在数据种类, 特征维度方面都有一定的区别, 比如说部分网格化监测中的小微型监测站所产生的监测数据并不包括当前时刻的温度, 湿度, 风向,气压等信息, 而且网格化监测中的小微型监测站所产生的监测数据之间除了具备天然的时间关联, 还由于小微型监测站之间的影响关系而具备空间关联. 所以在预测网格化监测中小微型监测站的空气中污染物浓度相关问题上使用以往常用的线性回归算法或者LSTM算法都会使预测结果由于温湿度等信息的缺失和空间特征的忽略而产生一定的误差.

因此为了有效的提取网格化监测中小微型监测站之间的空间关联特征和空气污染物数据之间天然的时间关联特征, 本文将能够有效且快速的提取非欧结构中的空间特征的图卷积神经网络(Graph Convolutional Network, GCN)与可以有效提取时序数据之间的时间特征的长短期记忆神经网络(LSTM)相结合, 提出了一种可以应用于网格化监测中空气质量预测的GCN-LSTM模型. 然后本文结合了沈阳市浑南区的14个小微型监测站的PM_2.5数据对本文提出的方法进行验证.

2 基于GCN-LSTM的空气质量预测模型

空气质量网格化监测中的各个小微型监测站的空间分布属于非欧式结构, 也就是说网格化监测中的每个小微型监测站周围的邻接监测站的个数和监测站之间距离是不确定的, 所以对网格化监测所产生的监测数据使用传统的卷积神经网络(Convolutional Neural Networks, CNN)并不能有效的提取数据之间的空间信息. 因此需要使用GCN来提取数据之间的空间特征, 并且使用LSTM来处理数据之间的时间特征, 最后再使用线性回归层来综合时空特征来产生比较准确, 有效的预测信息.

2.1 图卷积神经网络概述

图卷积神经网络(GCN)是一种以图数据为研究对象的卷积神经网络, 由Bruna等在2013年首次提出^[10]. 图卷积神经网络的出现为一些非欧的图数据的处理提供了新的思路, 比如GCN可以应用到社交网络分析, 推荐系统, 交通流量预测等^[11].

GCN的本质目的就是利用图卷积来提取非欧结构的图数据的空间特征, 根据文献[12]中提出的理论, 对于图 $G = (V,E,A)$ , 输入信号X和输出信号Y, 图卷积神经网络采取的处理方式f定义为:

$f(X,A) = Y$

(1)

其中, V表示图中的节点个数, $V = \left\{ {{v_i}} \right\}_{i = 1}^N$ 而E表示的边的集合, A是图的邻接矩阵, $A \in {R^{N\times N}}$ , 矩阵A中的元素 ${A_{ij}}$ 表示图G中节点 ${v_i}$ 和 ${v_j}$ 之间的连接关系. 图卷积的前向传播公式为:

${H^{(l + 1)}} = \sigma \left( {{\tilde D^{ - \textstyle\frac{1}{2}}}\tilde A{\tilde D^{ - \textstyle\frac{1}{2}}}{H^l}{W^l}} \right)$

(2)

式中, $\tilde A = A + I$ , I是大小为N×N的单位矩阵; $\tilde D$ 为对角矩阵, $\tilde D_{ii} = \displaystyle \sum\limits_j {{{\tilde A}_{ij}}} $ ; ${H^l} \in {R^{N\times D}}$ 表示第l层的输出值, 其中 ${H^0} = X$ ; $\sigma (\cdot)$ 表示激活函数; ${W^l}$ 表示第l层的参数值.

2.2 长短期记忆神经网络概述

LSTM网络是循环神经网络(Recurrent Neural Network, RNN)的一种变种^[13], 是由Hochreiter和Schmidhuber为解决RNN中的长期依赖问题在1997年首次提出. 由图1 RNN的示意图及其展开图可以看出, 虽然每个RNN单元都会将自身提取的信息传递给下一个单元, 但是当传递链的长度增加到一定程度的时候会出现信息丢失, 也就是上文提到的长期依赖的问题, 这也就促使了LSTM的出现与流行.

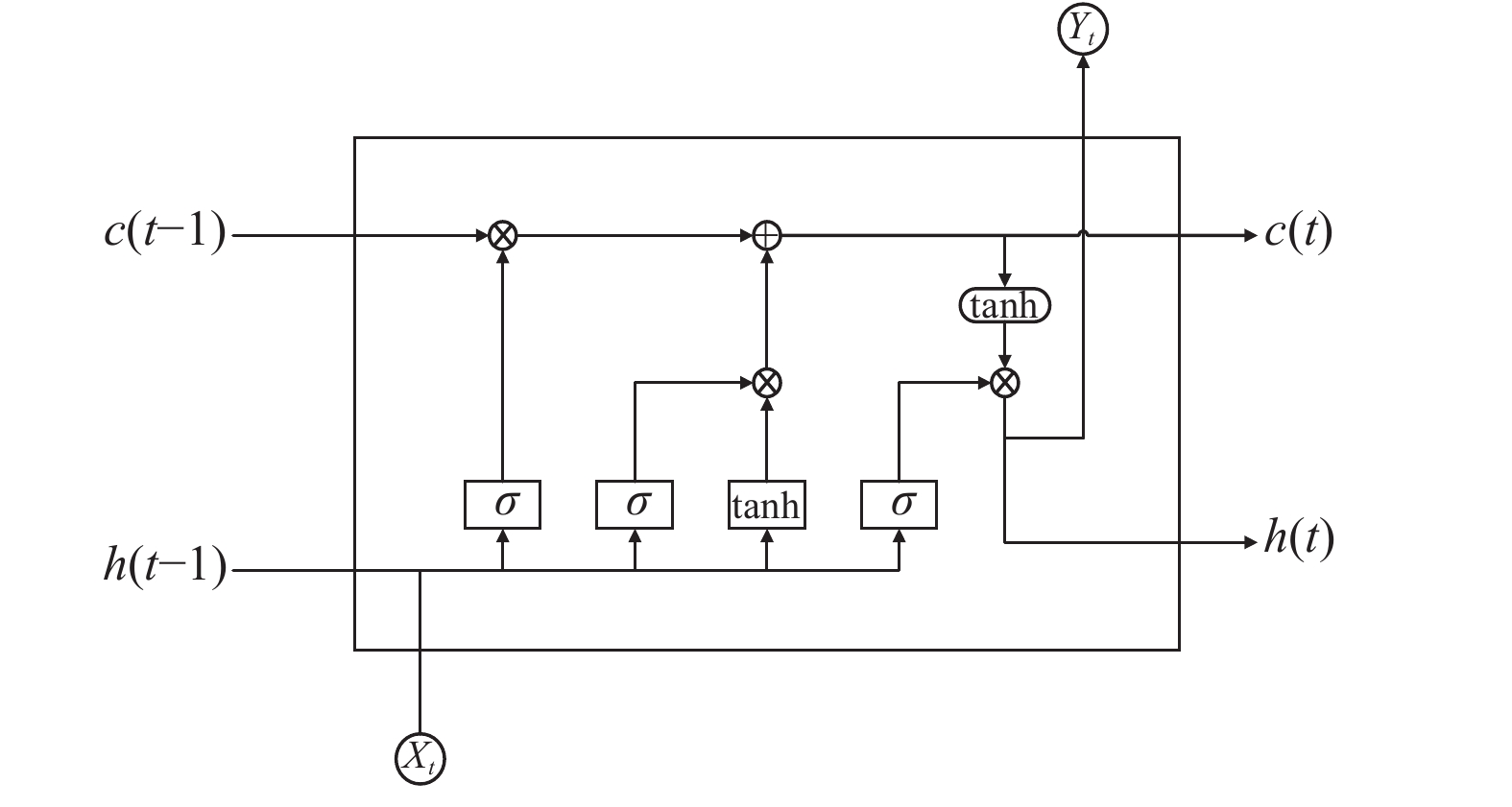
通过图2 LSTM的细胞结构示意图可以看出, LSTM采用了3种门控机制来解决传统RNN中的长期依赖问题.

LSTM的3种门控单元分别为: 遗忘门f, 输入门i和输出门o. 其中遗忘门用来控制当前细胞状态 ${C_t}$ 要丢弃哪些信息, 遗忘门的状态更新公式为:

${f_t} = \sigma ({W_f}[{h_{t - 1}},{x_t}] + {b_f})$

(3)

输入门控制了当前网络的输入 ${x_t}$ 会有多少保留到单元状态 ${C_t}$ 中, 输入门的状态更新规则为:

${i_t} = \sigma ({W_i}[{h_{t - 1}},{x_t}] + {b_i})$

(4)

${\tilde C_t} = \tanh ({W_c}[{h_{t - 1}},{x_t}] + {b_c})$

(5)

${C_t} = {f_t}\times{C_{t - 1}} + {i_t}\times{\tilde C_t}$

(6)

输出门控制了当前细胞状态能输出多少信息. 输出门的状态更新规则为:

${o_t} = \sigma ({W_o}[{h_{t - 1}},{x_t}] + {b_o})$

(7)

${h_t} = {o_t}\times\tanh ({C_t})$

(8)

式中, $\sigma $ 表示Sigmoid函数, 会根据输入产生[0,1]之间的向量; ${\tilde C_t}$ 表示的是候选细胞信息; ${W_f},{W_i},{W_o}, {W_c}$ 表示的是LSTM细胞状态更新过程中的权重系数矩阵; ${b_f},{b_i},{b_o},{b_c}$ 表示状态更新过程中的偏置矩阵.

2.3 GCN-LSTM模型

网格化监测中的小微型监测站的空气质量预测问题可以描述为: 通过小微型监测站时长为s的历史时刻数据 $[{X_{t - s}},\cdots,{X_{t - 1}}]$ 和各个监测站之间的空间关系A来预测下一个时刻t的空气质量 ${X_t}$ , 即:

${X_t} = F([{X_{t - s}},\cdots,{X_{t - 1}}],A)$

(9)

式中, ${X_t}$ 表示t时刻网格化监测体系中各个小微型监测站的空气中污染物的预测浓度; A表示不同小微型站之间的空间影响关系即邻接矩阵; F为处理方式, 在本文中F表示GCN-LSTM模型.

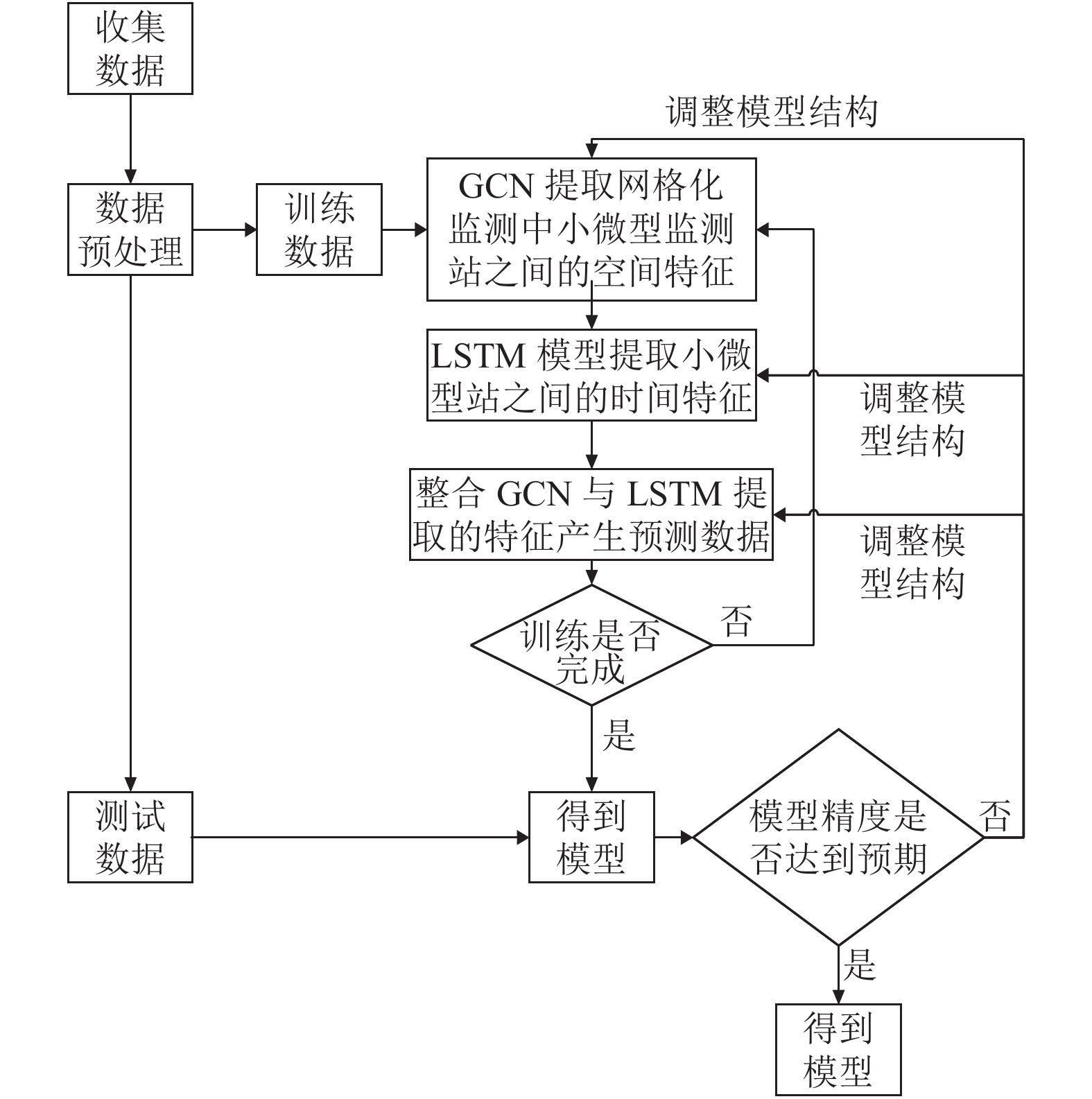
GCN-LSTM模型由图卷积神经网络和长短期记忆单元两部分组成, 如图3所示. 本次研究将长度为s的历史时间序列数据输入模型, 利用双层GCN结构解析网格化监测中小微型监测站的拓扑结构, 提取空间特征; 然后将具备空间特征的时间序列数据输入LSTM中学习时间特征, 最后通过一个线性回归层得到预测数据, GCN-LSTM模型具体的训练流程如图4所示.

首先将收集到的原始数据进行数据预处理和数据集划分, 然后将训练集和验证集组成的训练数据输入到如图3结构所示的GCN-LSTM模型中对模型进行训练; 最后将测试数据输入到训练完成的模型中观察模型的预测精度是否达到预期, 如果没有达到预期则调整模型GCN和LSTM中的隐层节点数然后再次训练直到得出达到预期精度的模型.

3 实验结果与分析 3.1 数据说明与预处理

本文使用的数据样本集为沈阳市浑南区14个小微型监测站的2020年1月到5月之间的PM_2.5浓度值, 数据采样的时间间隔是1小时, 每天可以获取336个样本数据.

部分原始数据如图5所示, 在图5中横轴代表的是PM_2.5原始数据的组数, 纵轴代表的是PM_2.5原始数据的浓度值. 从图上可以看出部分原始数据存在缺失和失真的情况. 因此在使用此数据集进行模型训练和验证之前需要对原始数据进行数据预处理, 补充缺失数据和清洗掉异常数据.

本文对于数据集中的缺失数据和异常数据采取的是如式(10)所示一元线性插值的方式进行数据补充和清洗, 同时采用式(11)对原始数据进行归一化使原始数据都映射到[0,1]之间.

${x_{a + i}} = {x_a} + \frac{{i({x_{a + j}} - {x_a})}}{j},0 < i < j$

(10)

式中, ${x_{a + i}}$ 为插值产生的补充数据, ${x_a}$ 为距离缺失数据最近的之前时刻的数据, ${x_{a + j}}$ 为距离缺失数据最近的之后时刻的缺失数据, $j$ 表示缺失数据的个数, $i$ 表示第 $i$ 个需要补充的缺失数据.

${\widetilde x_i} = \frac{{{x_i} - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}}$

(11)

式中, ${x_i}$ 为原始PM_2.5数据; ${\widetilde x_i}$ 为归一化后的PM_2.5数据; ${x_{\max }}$ 为原始数据中的最大值; ${x_{\min }}$ 为原始数据中的最小值.

3.2 实验环境

实验所用的硬件配置为: Intel(R) Core(TM)i5-5200U CPU@2.20 GHz, 8 GB内存; 实验所用的软件环境为: Windows10 (64位)操作系统, Python3.7, PyTorch1.5.0.

3.3 评价指标

本次研究的目的是预测网格化监测中的小微型监测站的空气质量和空气中污染物浓度的变化趋势, 所以为了能够更好的衡量预测的效果, 本文采用了2个评价指标: 绝对平均误差(Mean Absolute Error, MAE), 均方根误差(Root Mean Squared Error,RMSE), 来分析预测结果和真实测量值之间的偏差. 一般来说当预测值与真实值之间的偏差越小MAE和RMSE的值也就越小, 也就是说MAE和RMSE的值越小, 模型的预测效果越好.

$MAE = \frac{1}{N}\sum\nolimits_{i = 1}^N {\left| {{y_i} - {{\widehat y}_i}} \right|} $

(12)

$RMSE = \sqrt {\frac{1}{N}\sum\nolimits_{i = 1}^N {{{({y_i} - {{\widehat y}_i})}^2}} } $

(13)

式中, ${y_i}$ 为真实的PM_2.5浓度的测量值; ${\widehat y_i}$ 为PM_2.5浓度的预测值.

3.4 预测结果分析

本次研究将数据集以7:1:2的比例划分训练集, 验证集和测试集, 并且使用长短期记忆神经网络作为对比模型, 模型的训练过程如算法1所示.

算法1. 模型搭建与训练

输入: 时间序列长度 $\scriptstyle s $ , 小微型监测站所构成的图的邻接矩阵 $\scriptstyle A \in {R^{N\times N} }$ , PM_2.5的浓度表示 $\scriptstyle C \in {R^{N\times M}}$ , 模型选择标志flag

输出: 训练好的模型

1. 对邻接矩阵A添加自连接, 并对自连接后的邻接矩阵进行对称归一化处理.

2. 对PM_2.5的浓度数据C进行归一化并且构建数据集D.

3. for $\scriptstyle m < M$ do

4. $\scriptstyle{X_m} \leftarrow \left[ {x_m^1,x_m^2,\cdots x_m^N} \right]$

5. $\scriptstyle m \leftarrow m + 1$

6. end

7. for $\scriptstyle[{X_{t - s}}\cdots{X_t}] \in C$ do

8. $\scriptstyle D \leftarrow \{ X = [{X_{t - s}}\cdots{X_{t - 1}}],Y = {X_t}\} $

9. $\scriptstyle t \leftarrow t + 1$

10. end

11. 按照7:1:2划分数据集D得到训练集train, 验证集valid和测试集test

12. if flag == LSTM do

13. 使用PyTorch搭建一个隐层节点数分别为80, 108和36的3层LSTM网络.

14. else if flag == GCN-LSTM do

15. 搭建如图3所示的GCN-LSTM模型.

16. end if

17. repeat

18. 从train中随机选取batch为64的数据输入模型进行训练.

19. 以MSE作为loss, 使用Adam算法以1e–4为学习率更新权重.

20. until 满足停止条件.

21. 返回训练完成的模型.

实验中分别采用LSTM和GCN-LSTM两种模型使用14个小微型监测站过去12个小时的PM_2.5数据来预测未来1小时的PM_2.5浓度, 预测结果对比如表1所示.

从表1中两种模型的对比可以看出, 本文所提出的GCN-LSTM模型在大多数小微型监测站中MAE和RMSE这两种评价指标的数值都要比使用LSTM模型的值要小. 而且这两种评价指标都是越小就代表模型的预测值与实际的测量值之间的偏差越小, 也就是说在网格化监测中小微型监测站的PM_2.5的预测问题上, 本文提出的模型的预测效果要优于以往研究中所使用的LSTM模型.

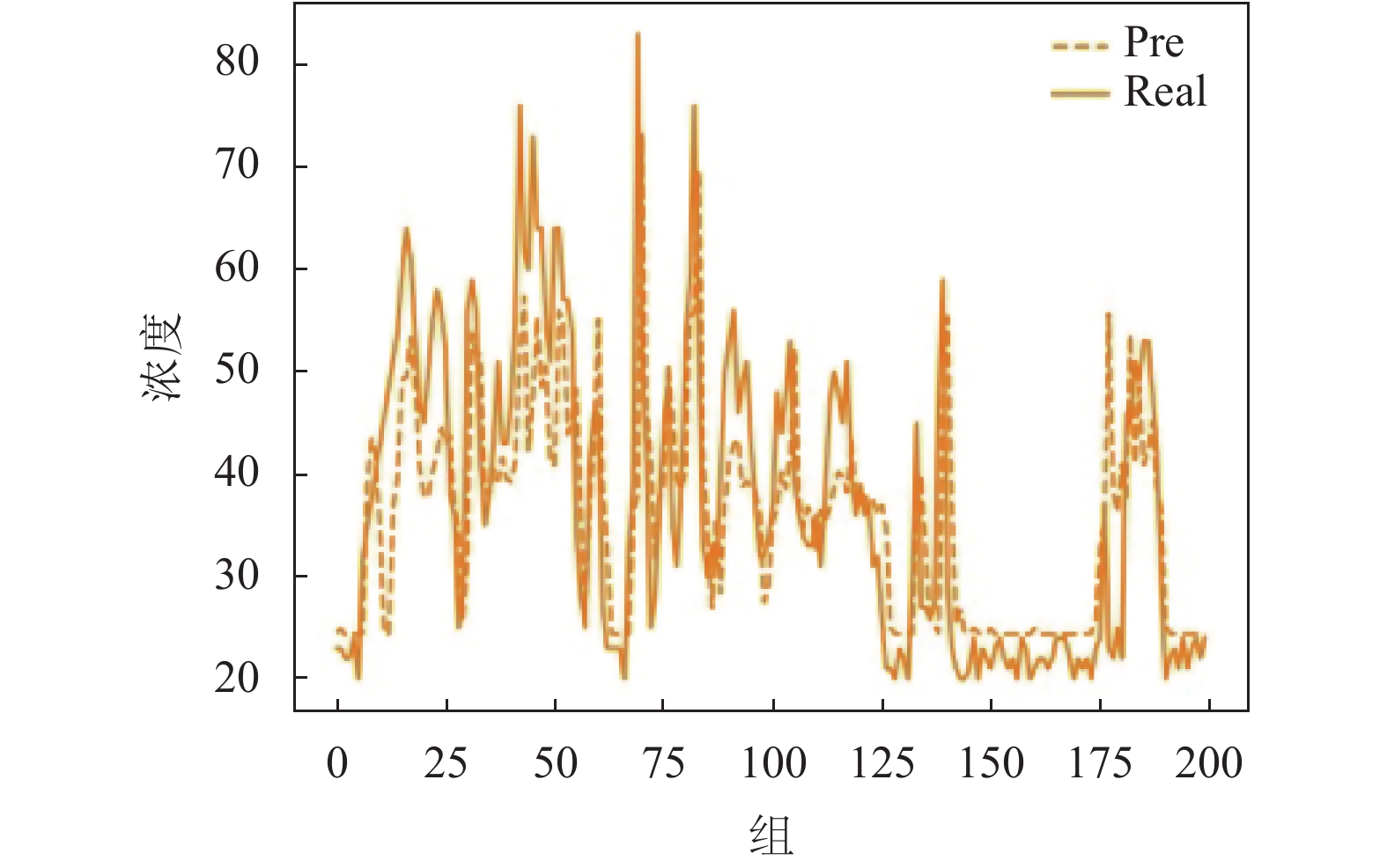
图6和图7分别为实验中预测效果最好的监测站点全运路监测点和预测效果最差的南屏东路监测点的部分预测结果. 图6和图7中的横轴代表第几组测试数据, 纵轴代表PM_2.5的浓度值, pre代表有GCN-LSTM模型产生的PM_2.5浓度的预测值, real代表当前监测站的实际的PM_2.5的监测值. 从图上的预测曲线与实际测量值的曲线的拟合程度来看, 无论是全运路监测点还是南屏东路监测点, 预测曲线的变化趋势都大致与实际的测量值的曲线的变化趋势相同. 这都说明了GCN-LSTM模型可以有效的预测网格化监测中的小微型监测站的PM_2.5的变化趋势, 为我国环境监测和治理提供一定的参考.

4 结论与展望

针对时空关联性高的网格化监测中的小微型监测站的空气质量预测问题, 本文提出了一种基于GCN-LSTM的空气质量预测方法. 尝试通过使用GCN算法从监测站的拓扑图中提取有效的空间特征, 并采用LSTM来学习以往空气中污染物浓度数据中的时间特征, 最后采用一个线性回归层来整合特征并产生预测结果, 进而提高网格化监测中小微型监测站空气质量预测的精度. 实验结果表明本文的GCN-LSTM算法在网格化监测中的小微型监测站空气质量的预测问题上要比LSTM算法表现更优. 未来, 将对GCN-LSTM模型结构进一步优化, 研究更有效的缺失数据和异常数据的处理方法, 从而提高模型的整体预测效果和精度.