近年来云数据中心的构造与使用成了政府和各大IT企业越来越重视的问题, 为了倡导绿色云计算, 云数据中心的构造目标是低能量消耗、高服务质量(Quality of Service, QoS)、节省物理空间和高可靠性等[1-3]. 一个数据中心(Data Center, DC)通常配置有大量的紧密堆积在一起物理节点(Physical Machines, PMs), 目的是提高建筑物空间的利用率; 虚拟化技术是云数据中心中最重要的技术, 虚拟化允许用户对云资源的访问是透明与简单方便的, 它通过虚拟机(Virtual Machines, VM)的形式将应用程序封装在虚拟机之中, 通过虚拟机分配策略将其分配到具体的数据中心的物理节点之中执行. 所以虚拟机分配(Virtual Machine Distribution, VMD)等策略很大程度上影响了云平台的整体性能, 目前大量的文献把性能指标关注在SLA违规比率、服务质量QoS、系统能量消耗、虚拟机迁移次数等方面[4].
虚拟机分配的理想目标是尽量利用个数比较少的云数据中心, 同时提高每个数据中心的云资源利用效率, 在此基础上提高云数据中心的灵活性和可用性, 降低硬件成本和操作成本(能量消耗, 物理空间占用等)[5].
本文设计了一种用于企业的云数据中心的工作场景, 它可以接受大量客户端的虚拟机的请求, 并将这些虚拟机分配到云数据中心的具体物理节点执行. 参考了经典的装箱问题(classical in packing problem)模型, 包括经典的最好适应算法Best-Fit-Algorithm (BFA)、首次适应算法First-Fit-Algorithm (FFA), 下次适应算法Next-Fit-Algorithm (NFA)、最坏适应算法Worst-Fit-Algorithm (WFA)和随机算法Random Allocation -Algorithm (RAA)等来将大量的虚拟机放置到各个数据中心的物理节点完成云计算. 建立了虚拟机放置过程中各种约束因素的数学模型, 利用贪心算法(greedy algorithm)优化云数据中心之间的虚拟机放置策略. 测试结果表明, 经过优化的最好适应算法BFA具有比较好的性能, 这对于其他企业建立与构造云数据中心有比较好参考价值.
1 相关工作目前学术界针对云端的虚拟机分配与迁移策略, 进行了大量的研究. 主要分为两类, 第一类是针对从虚拟机到单数据中心中的物理节点的分配与迁移. 第二类是针对从虚拟机到多个云数据中心的分配与调度. 前一类关注的虚拟机在物理节点之间的选择、分配和迁移; 后者关注的是虚拟机在多个云数据中心的分配与放置.
针对第一类问题, 例如文献[6]提出并评价了云端多虚拟机迁移的负载与性能变化; 文献[7]提出了一种利用动态放置应用程序的方法EnaCloud, 实现云平台的能效管理. 文献 [8]同样从CPU维度对虚拟机的动态配置问题进行建模, 并利用改进的蚁群算法进行求解. 文献[9]提出了PS-ABC算法, 该方法能够在长期服务项目的局部时间段内实现较好节能效果, 但是在服务项目全局的能耗优化问题上, 效果并不理想. 文献[10]在此基础上提出了PS-ES启发式算法, 不仅实现了当前场景的能源优化, 而且也有效降低了长期服务项目总体的能源消耗, 但其考虑的维度较单一. 文献 [11]在Beloglazov研究的基础上提出(Service Level Agreement, SLA)违规算法, 引入最小能源最大利用率策略, 进一步优化虚拟机配置方法.
针对第二类研究, 主要涉及到经典装箱问题, 此类问题是一个基于多约束的整数规划问题, 同时也是一个NP-hard问题. 即将云数据中心抽象为箱子, 箱子的容量是云数据中心资源的大小, 包括物理服务器个数、CPU主频高低、CPU内核个数, 内存大小、空余磁盘空间大小和应用程序类型等; 虚拟机抽象为装入的物品. 例如文献[12]利用装箱问题提出了启发式算法, 但是它们考虑的维度比较单一. 文献[13]提出了向量装箱和多维装箱问题, 文献[14]采用了首次适应减少算法(First-Fit Decreasing, FFD)来提高装箱性能与效果. 文献[15]采用遗传算法来优化资源的消耗, 能量的消耗和虚拟机的放置. 文献[16]将多虚拟机放置设计为一个多目标约束满意问题, 目标是为了最小化物理节点个数和虚拟机迁移次数. 文献[17]利用了约束编程模式, 采用一个灵活和能量相关的框架来分配虚拟机到各个云数据中心.
在贪心算法方面文献[18,19]提出了云计算中的基于贪心算法的任务调度及改进, 把改进任务竞争时间和改进任务执行代价作为主要因素. 实验结果表明贪心算法在串行调度算法的基础上可以改进任务调度的性能, 但是它们并没有将贪心算法使用到物理资源使用和低能量消耗相关的算法之中, 也没有用来优化云端的虚拟机到数据中心的分配.
最近这三年又有文献提出采用软件的方法来提高虚拟机分配和虚拟机放置策略的性能, 还有文献提出需要在虚拟机迁移过程中考虑网络攻击危险, 保证云数据中心的可靠性. 例如文献[20]把虚拟机迁移过程划分为物理主机状态检测、虚拟机映射、虚拟机选择、虚拟机放置4个复杂的步骤, 虚拟机映射主要通过任务粒度、软件代价等来进行调整; 虚拟机放置属于一类经典装相问题, 即把大量的虚拟机VM放置到大量的物理节点之中, 它提出要考虑虚拟机映射和虚拟机放置之间的相互联系的算法来改善性能. 文献[21] 提出了云数据中心基于安全检测的虚拟机迁移策略. 利用隔室技术及SIR (Susceptible, Infected, Recovered)模型在虚拟机迁移过程将有安全威胁的虚拟机隔离出来, 保证云数据中心的能量消耗与安全威胁的平衡.
本文提出的虚拟机分配策略属于第二类方法, 主要针对从虚拟机到云数据中心的分配, 考虑的问题装箱问题的维度不仅是硬件条件, 还有软件条件, 采用贪心算法进行优化, 即在虚拟机分配的时候只要局部的各个维度的资源最高即可得到资源, 完成分配.
2 贪心算法的虚拟机分配策略描述 2.1 虚拟机分配的层次结构本文提出的云数据中心的虚拟机分配的工作场景如图1, 包括3层的逻辑结构: 用户层、云服务提供者层、云数据中心集层.
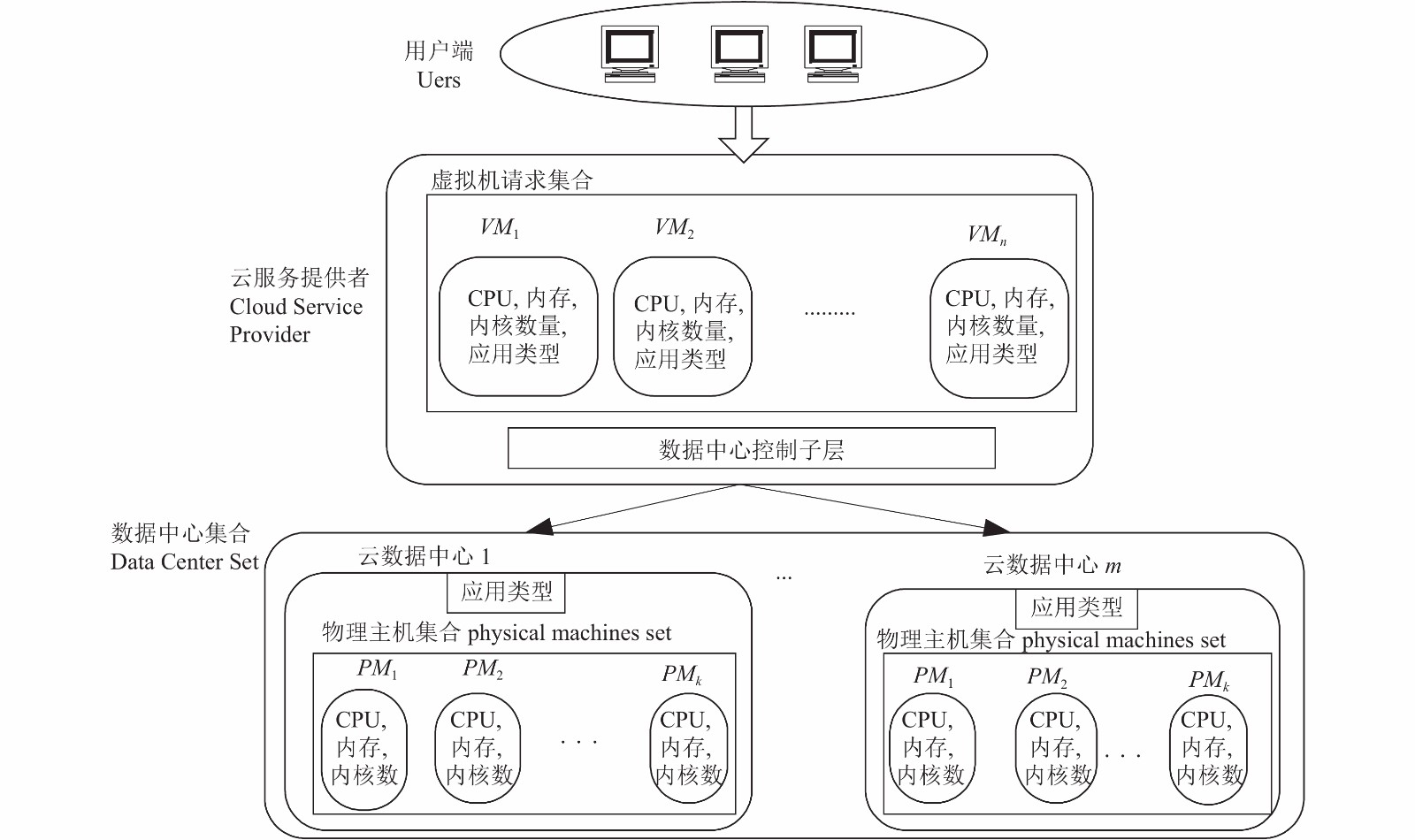
|
图 1 贪心算法的虚拟机分配工作场景 |
用户层Users处于顶层. 所有的应用程序的请求在这一层产生, 并形成虚拟机请求集(VM Request Set, VMRS)它们将被发送到下一层: 云服务提供者层(Cloud Service Provider Layer, CSPL).
中间层CSPL包括两个子层, 上面的子层全部是来自用户层的虚拟机请求集. 虚拟机请求由CPU使用率、内存大小、内核数目、应用程序类型(基于CPU的请求或基于I/O的请求)组成. 下一子层是(Data Center Control Layer, DCCL)数据中心控制层, 它拥有虚拟机请求和各个数据中心的信息, 虚拟机分配过程中要考虑各种约束条件, 包括资源是否满足约束条件、用户请求约束条件、用户端和CSP之间的SLA约束条件等.
所有的虚拟机请求都被放置到云数据中心被执行, 所以最下一层是(Data Center Set Layer, DCSL) 云数据中心集层. 数据中心集层的功能是完成被分配到每个具体的数据中心的虚拟机到其下物理节点的分配.
本文是假设每个云数据中心的节点是同构条件下的物理节点, 同构条件下的计算机在统计其计算能力和存储能力的时候可以按照线性关系累加. 同时该工作场景下的所有云数据中心在同一个地理位置, 这样各个物理主机的网络带宽基本类似.
2.2 虚拟机分配的多维约束描述我们把各个云数据中心的最大能量消耗和最小能量消耗分别定义为energymax和energyidle. 被分配到各个云数据中心的虚拟机也定义了一个与其相关的代价变量dcprice, dcprice的数值相当于是一种资源需求, 就是混合多个维度的资源需求. 虚拟机分配主要用来处理n个虚拟机的请求, 每个虚拟机
DC集合中的云数据中心必须记录一个具体的价值参数dcprice, 该dcprice为放置到该DC中的虚拟机的多维的资源请求数值, 在云计算的服务等级协议SLA协议中, 在用户User和云服务提供者CSP之间, 该价值dcprice为固定不变的. 利用一个向量来表示DC集合中的所有数据中心中的价值:
| $\left\{\!\!\!\! \begin{array}{l} energymax vector = \left\{ {dce{{max }_1},dce{{max }_2},\cdots ,dce{{max }_m}} \right\}\\ energyidlevector = \left\{ {dceidl{e_1},dceidl{e_2},\cdots ,dceidl{e_m}} \right\} \end{array}\right. $ |
根据前面的思路, 认为把虚拟机请求集放置到具体的云数据中心为装箱问题, 我们需要考虑的问题的约束条件和维度具体包括:
1)应用程序请求调度约束条件: 这个约束将考虑虚拟机请求的所有维度参数, 包括虚拟机请求的CPU使用率、内存大小、内核数目、请求类型(基于CPU的请求或基于I/O的请求).
2)能力约束条件(capacity). 这个约束主要是判断云平台的整体的资源使用状态, 虚拟机请求集的整体资源需求之和必须小于或者等于云数据中心的整体资源, 当然这个资源数据必须考虑多个维度之总和.
3)放置约束条件. 这里约束了如果整体资源已经足够, 可以只从云数据中心集合中选择一个云数据中心, 它们要求尽量少的使用云数据中心.
2.3 贪心算法优化的虚拟机分配方法根据前面提到的, 在虚拟机分配的时候假设每个DC中有k个物理主机PM, 设计
| $CD{C_r}(i) = \sum\limits_{j = 1}^k {CP{M_r}} (i)$ | (1) |
这里
| $ CDCSE{T_r} = \sum\limits_{j = 1}^m {CD{C_r}} (j) $ | (2) |
类似于式(2), 我们定义n个虚拟机请求组成的虚拟机请求集的整体资源需求能力(capacity)为式(3):
| $ CVMRSE{T_r} = \sum\limits_{j = 1}^n {CV{M_r}} (j) $ | (3) |
这里
| $UD{C_r}(j) = \frac{{\displaystyle\sum\limits_{i = 1}^n {CV{M_r}} (j)*{V_{ij}}}}{{CD{C_r}(j)}};\;\forall j \in \left\{ {1,2,\cdots, m} \right\}$ | (4) |
如果
| $\left\{\!\!\! \begin{array}{l} dcpricevector = \left\{ {dcpric{e_1},dcpric{e_2},\cdots,dcpric{e_m}} \right\}\\ energy\max vector = \left\{ {dce{{max }_1},dce{{max }_2}, \cdots,dce{{max }_m}} \right\}\\ energyidlevector = \left\{ {dceidl{e_1},dceidl{e_2}, \cdots,dceidl{e_m}} \right\} \end{array}\right. $ |
如果把能量最大向量和能量最小向量考虑进去, 那么云数据中心
| $ \begin{split} energyDC(j) = &((dce{max_j} - dceidl{e_j})\times \max \{ UD{C_r}(j)\}\\ & + dceidl{e_j},\;\;{\text{其中}},\forall j \in \left\{ {1,2,\cdots, m} \right\} \end{split} \!\!\!\!\!\!\!\!\!\!\!\!\!\! $ | (5) |
式中,
| $TEC = \sum\limits_{j = 1}^m {energyDC} (j)$ | (6) |
与每个数据中心关系密切的这两个参数就是在跨数据中心进行虚拟机分配的总价值参数dcprice和其对应的能量消耗参数TEC. 我们定义
| $ {fnDC(\!j\!)\!\! =\!\! \left\{ {{\omega _{\rm en}}\!\times\! energyD{C_r}(j)} \right\}} { \!+\! \left\{ {{\omega _{\rm ex}}\!\times\!\left(\!\! {\sum\limits_{i = 1}^n \!{dcpric{e_j}\!\times\!{V_{ij}}}\!\! } \right)} \right\}} $ | (7) |
这里
| $overallfnDC = \sum\limits_{j = 1}^m {fnDC} (j)$ | (8) |
overallfnDC是所有在DC集中的每个
| $\sum\limits_{i = 1}^n {CV{M_r}} (i)*{V_{ij}} \le CD{C_r}(j);\;\forall j \in \{ 1,2,\cdots,m\} $ | (9) |
| $\sum\limits_{i = 1}^n {CV{M_r}} (i) \le CDCSE{T_r}$ | (10) |
| $\sum\limits_{j = 1}^m {{V_{ij}}} = 1;\;{\forall _i} \in \{ 1,2,\cdots,n\} $ | (11) |
| ${V_{ij}} \in \{ 0,1\} ;\;\forall i \in \{ 1,2,\cdots,n\} ,\forall j \in \{ 1,2,\cdots,m\} $ | (12) |
式(9)满足了前面提到的虚拟机调度约束条件; 式(10)满足了资源使用能力约束条件; 式(11)和式(12)满足了虚拟机放置约束条件, 一个虚拟机只能放置到惟一的云数据中心, 因为通过
虚拟机分配是一个NP-Hard问题, 本文应用贪心算法的启发式算法, 参考前面公式中计算的overallfnDC总体价值参数和总能量消耗TEC参数, 将虚拟机请求集放置到目标函数最合适的云数据中心之中.
云数据中心控制层使用和收集虚拟机请求集的所有信息, 数据中心集
在针对应用程序虚拟机分配时, 本文把贪心启发式算法应用到经典的装箱问题解决办法之Random Allocation Algorithm (RAA)随机选择算法、下次适应算法Next Fit Allocation (NFA)、首次适应算法First Fit Allocation (FFA)、最好适应算法Best Fit Allocation (BFA) 和最坏适应算法Worst Fit Allocation (WFA)之中.
利用某个企业的4个大规模云数据中心作为测试环境, 访问云服务器的客户端的物理节点硬件组成情况如下表1, 云数据中心的物理节点情况配置如表2, 虚拟机请求通过一个统一的Web应用程序访问, 主要包括3类虚拟机, 每个虚拟机对资源的请求需求如表3.
为了仿真需要, 实验中改变虚拟机请求个数从25到250个, 其中步长为25. 因为本文利用的云数据中心中的物理主机是同构的, 且每个云数据中心中的主机个数是常量, 所以针对启发式算法而言, 首次适应算法FFA和最好适应算法BFA的实验结果应该是一样的, 所以我们的实验结果统计主要针对于RRA、WFA、BFA、NFA四类算法.
| 表 1 云客户端配置 |
| 表 2 云数据中心中的物理节点配置 |
| 表 3 应用程序端的虚拟机需求情况 |
3.2 云数据中心的数量测试
表4显示了随着虚拟机数目的增加, 被分配了云数据中心的个数的变化情况, 从表可以看出, NFA, BFA及RAA三类启发式算法
| 表 4 云数据中心个数随的虚拟机请求的变化(单位:个) |
因此, 每个虚拟机被放置到数据中心的时候, 它将都被访问到, 进一步观察结果可以得到, BFA比NFA使用更加少的云数据中心个数, 这是因为在分配虚拟机的时候, BFA算法首先考虑的是云数据中心, 而NFA算法往往首先考虑的是数据中心中的之前的虚拟机分配情况.
3.3 云数据中心的整体代价测试表5显示了随着虚拟机请求数量的变化, 云平台的整体资源参数dcprice的变化. 由于表4已经表明被分配虚拟机的云数据中心数量是随着虚拟机请求个数的增加, 基于这个事实, 价值向量dcpricevector也就是系统所包含的软硬件资源数量也是随着云数据中心的增加而增加, 整个系统的总体资源可以通过式(13)进行计算.
| $\left\{ \begin{split} &Totalprice = \sum\limits_{j = 1}^m {\sum\limits_{i = 1}^n {dcpric{e_j}\times{V_{ij}}} }\\ &{V_{ij}} \in \{ 0,1\} ,\;\forall i \in \{ 1,2,\cdots,n\} ,\;\forall j \in \{ 1,2,\cdots,m\} \end{split}\right. $ | (13) |
如果
| 表 5 云数据中心总价值向量随着的虚拟机请求个数的变化 |
表5的结果表明BFA启发式算法比NFA算法随着虚拟机请求数量的变化, 它增加得比较缓慢, 它们之间的差异几乎可以忽略; RAA算法和WFA算法的总体价值是不一致的, 因为总体价值主要依赖于虚拟机请求被分配到的一个具体云数据中心.
3.4 系统整体能量消耗测试表6显示了随着虚拟机个数请求变化, 云平台的总体能量消耗情况, 能量消耗的通过式(6)进行计算, 和表4和表5比较起来, BFA和WFA两个被优化的贪心算法之间的差异不是很大, 得到这种结果的原因是能量消耗的大小主要依赖于一个具体的云数据中心的利用效率, 而不是云数据中心的被分配个数; WFA和RA两个算法中云数据中心的利用效率要低于NFA和BFA算法. NFA和BFA算法中的云数据中心的资源利用效率比较高; 整体来所能量消耗都是随着虚拟机请求个数的增加而增加.
3.5 目标函数代价测试表7显示了随着虚拟机请求个数的增加, 系统的总体的代价函数值overallfnDC变化情况. overallfnDC主要通过式(8)来进行计算, 同时满足式(9)~式(12)的约束条件, overallfnDC主要考虑了2类约束条件, 能量TEC和总体价值dcprice. 如果两个权重值都设置为0.5, 那么能量TEC和总价值fnDC都平衡考虑.
从表7中可以看出, 如果既考虑云数据中心的数量也考虑云数据中心的使用效率, 那么BFA和WFA两个算法的差异比较小. NFA和FFA算法的差异要小于WFA和RAA算法, 因为
| 表 6 云数据中心能量消耗随着的虚拟机请求个数的变化(单位: kWh) |
| 表 7 云数据中心总体价值随着的虚拟机请求个数的变化 |
所有上面的实验结果图都显示BFA最好适应算法在跨云数据中心的虚拟机分配的启发式算法中具有比较好的性能.
4 结论与展望本文运用贪心算法优化了传统的虚拟机分配算法, 云数据中心的物理节点规模将持续不断扩大, 这样将导致能量消耗的增加和资源规模总价值的增加, 本文主要考虑了这两个重要参数, 讨论了虚拟机分配的三类主要约束条件. 但是随着云平台上的应用程序的种类增加和可用性的需求, 为了完成高服务质量QoS的需求, 云数据中心的虚拟机分配需要考虑更加多的维度, 这个是本文的后续工作.
| [1] |
Mann ZÁ. Resource optimization across the cloud stack. IEEE Transactions on Parallel and Distributed Systems, 2018, 29(1): 169-182. DOI:10.1109/TPDS.2017.2744627 |
| [2] |
Lei Z, Sun EX, Chen SB, et al. A novel hybrid-copy algorithm for live migration of virtual machine. Future Internet, 2017, 9(3): 37. DOI:10.3390/fi9030037 |
| [3] |
Jin XB, Zhang F, Wang L, et al. Joint optimization of operational cost and performance interference in cloud data centers. IEEE Transactions on Cloud Computing, 2017, 5(4): 697-711. DOI:10.1109/TCC.2015.2449839 |
| [4] |
Thiruvenkadam T, Karthikeyani V. An approach to virtual machine placement problem in a datacenter environment based on overloaded resource. International Journal of Computer Science and Mobile Computing, 2014, 3(6): 837-842. |
| [5] |
Gao YQ, Guan HB, Qi ZW, et al. A multi-objective ant colony system algorithm for virtual machine placement in cloud computing. Journal of Computer and System Sciences, 2013, 79(8): 1230-1242. DOI:10.1016/j.jcss.2013.02.004 |
| [6] |
Dad D, Yagoubi D E, Belalem G. Energy efficient VM live migration and allocation at cloud data centers. International Journal of Cloud Applications and Computing, 2014, 4(4): 55-63. DOI:10.4018/ijcac.2014100105 |
| [7] |
Li B, Li JX, Huai JP, et al. EnaCloud: An energy-saving application live placement approach for cloud computing environments. Proceedings of 2009 IEEE International Conference on Cloud Computing. Bangalore, India. 2009. 17–24.
|
| [8] |
Liu XF, Zhan ZH, Deng JD, et al. An energy efficient ant colony system for virtual machine placement in cloud computing. IEEE Transactions on Evolutionary Computation, 2018, 22(1): 113-128. DOI:10.1109/TEVC.2016.2623803 |
| [9] |
Xu GC, Ding Y, Zhao J, et al. A novel artificial bee colony approach of live virtual machine migration policy using Bayes theorem. The Scientific World Journal, 2013, 2013: 369209. |
| [10] |
Zhao J, Hu L, Ding Y, et al. A heuristic placement selection of live virtual machine migration for energy-saving in cloud computing environment. PLoS One, 2014, 9(9): e108275. DOI:10.1371/journal.pone.0108275 |
| [11] |
Cao ZB, Dong SB. An energy-aware heuristic framework for virtual machine consolidation in cloud computing. The Journal of Supercomputing, 2014, 69(1): 429-451. DOI:10.1007/s11227-014-1172-3 |
| [12] |
Feller E, Rilling L, Morin C. Energy-aware ant colony based workload placement in clouds. Proceedings of the 2011 IEEE/ACM 12th International Conference on Grid Computing. Lyon, France. 2011. 26–33.
|
| [13] |
Kaaouache MA, Bouamama S. Solving bin packing problem with a hybrid genetic algorithm for VM placement in cloud. Procedia Computer Science, 2015, 60: 1061-1069. DOI:10.1016/j.procs.2015.08.151 |
| [14] |
Mishra M, Sahoo A. On theory of VM placement: Anomalies in existing methodologies and their mitigation using a novel vector based approach. Proceedings of the 2011 IEEE 4th International Conference on Cloud Computing. Washington, DC, USA. 2011. 275–282.
|
| [15] |
Joseph CT, Chandrasekaran K, Cyriac R. A novel family genetic approach for virtual machine allocation. Procedia Computer Science, 2015, 46: 558-565. DOI:10.1016/j.procs.2015.02.090 |
| [16] |
Hermenier F, Lorca X, Menaud JM, et al. Entropy: A consolidation manager for clusters. Proceedings of 2009 ACM SIGPLAN/SIGOPS International Conference on Virtual Execution Environments. Washington, DC, USA. 2009. 41–50.
|
| [17] |
Dupont C, Schulze T, Giuliani G, et al. An energy aware framework for virtual machine placement in cloud federated data centres. Proceedings of the 3rd International Conference on Future Systems: Where Energy, Computing and Communication Meet. Madrid, Spain. 2012. 1–10.
|
| [18] |
Choudhary M, Peddoju SK. A dynamic optimization algorithm for task scheduling in cloud environment. International Journal of Engineering Research and Applications, 2012, 2(3): 2564-2568. |
| [19] |
Sharma RK, Sharma N. A dynamic optimization algorithm for task scheduling in cloud computing with resource utilization. International Journal of Scientific Engineering and Technology, 2013, 2(10): 1062-1068. |
| [20] |
Mann ZÁ. Interplay of virtual machine selection and virtual machine placement. Proceedings of the 5th European Conference on Service-Oriented and Cloud Computing. Vienna, Austria. 2016. 137–151.
|
| [21] |
Ahamed F, Shahrestani S, Javadi B. Security aware and energy-efficient virtual machine consolidation in cloud computing systems. Proceedings of 2016 IEEE Trustcom/BigDataSE/ISPA. Tianjin, China. 2016. 1516–1523.
|
 2021, Vol. 30
2021, Vol. 30



