网络通信技术的进步促使社交网络成为信息传播的重要渠道. 人们通过智能终端发表观点, 表达意见, 与之相伴产生的网络舆情问题已经成为相关机构关注的热点. 以新浪微博为例, 截至2019年底, 微博月活跃用户达到5.16亿, 其海量舆情数据已经达到了让任何部门、机构都无法忽视的地步. 当前基于舆情热度的研究多数是针对一些具体的热门事件或热门话题, 无法从宏观的角度把握目标群体的整体舆情动态, 以广义的舆情“关键词”作为热度的研究对象, 如“手机”、“农产品”、“房价”、“比特币”、“疫情”等, 对企业产品精准营销, 政府部门舆情监测将更具有宏观指导意义. 目前对公众开放的基于关键词的大数据分析平台主要有百度指数、微指数、头条指数等, 这类平台虽然能够提供一些关键词的分析数据, 但由于侧重点不同, 并不能满足对舆情热度需求的个性化分析. 为此, 本文以微博数据为基础, 提出了一种结合因子分析、遗传算法的Elman网络模型对舆情关键词热度进行分析预测, 以期为相关决策提供支持.

1 研究现状

通过相关研究文献的梳理, 网络舆情热度的研究方法主要有两类:

一类是根据事物发展的规律, 基于时间序列挖掘自身历史数据进行热度的分析和预测. 王宁等^[1]采用灰色系统理论拟合时间序列指数对诉讼案件热度进行了预测和分级管理问题. 陈福集等^[2]采用改进的ABC-BP模型对“天津港爆炸事件”的百度指数热度走势进行了预测研究. 刘巧玲等^[3]通过一种改进SIR传染病传播模型, 以“魏则西”事件发生前三天的数据来预测事件后续传播趋势. 高颖^[4]采用LS-SVM算法对2018年哈尔滨市发生的“8.25”火灾事件进行回归建模从而预测其短期热度值. 这些针对特定事件的舆情热度预测方法均能取得较好的预测效果, 但对于舆情关键词这种宽泛的指标, 并不符合特定事件舆情热度从产生、爆发到衰退的规律, 时间序列越长, 信息越分散, 其波动更多呈“随机”状态. 虽然林育曼等^[5]构造了ARIMA-BP神经网络模型将预测对象视为随机序列来近似逼近, 取得较好的拟合效果. 但对于突发值的预测往往不是很准确.

另一类是通过挖掘自身数据特征, 找到与舆情热度的关联关系, 从而进行热度的分析和预测. 郑志蕴等^[6]提出一种基于多特征的热门微博预测算法, 利用信息增益算法对微博特征热度进行度量, 结BP神经网络来预测是否为热门微博. 谢修娟等^[7]提出一种基于密度的K-means算法从微博内容中抓取热词, 分析舆情热点. 兰月新等^[8]基于灰色关联度方法构建网络舆情热度模型, 定性分析了网络舆情热度影响因素. 这些方法通过自定义热度计算公式, 采用分类和聚类算法预测的舆情热度的发展趋势, 都具备较高的准确率和稳定性, 但由于没有客观指标的量化分析, 对于舆情关键词的热度研究存在一定的局限性. 同时各特征对热度指标的究竟有多大的贡献还需进一步研究分析.

针对以上研究存在的局限, 本文以新浪微博为例, 设计了一种新的组合模型可有效提高网络舆情关键词热度的预测精度. 首先选取并量化影响舆情关键词热度的特征指标, 采用因子分析方法提取其中贡献较大的影响因子, 剔除影响预测精度的噪声冗余, 然后将影响因子输入到Elman网络中计算预测结果. 为进一步提高预测精度, 一方面通过增加神经元个数来反馈调节模型预测结果, 另一方面利用遗传算法优化网络权值和初始参数, 最终实现舆情热度及其发展趋势的预测.

2 模型构建 2.1 特征量化

以新浪微博公开可挖掘数据为例, 与舆情热度有关的特征一般包括博主特征、博文特征和传播特征. 博主特征包括博主ID(或昵称)、博主类型(即认证身份)、关注数、粉丝数和微博数等^[9], 博主特征决定了它的受众范围, 即热度传播的广度. 博文特征包括博文的长度、博文元素(图片、视频、链接、表情符号)、博文内容(所表达的情感)以及发布时间, 一般博文长度和舆情热度呈正相关态势, 博文所含元素越丰富越能吸引读者的关注, 内容情感的表达可以引起读者的共鸣, 可以说博文特征决定了舆情热度的传播强度. 传播特征包括微博的转发数、评论数、点赞数以及发布平台(PC端、手机端等)^[10], 传播特征是舆情热度最直接的反映, 决定的舆情热度最终传播的深度. 为了能更好的分析热度影响因素, 需要将特征信息中非量化信息进行量化, 如表1所示, 根据这些信息对热度的影响关系, 从高到低依次赋分.

博文长度可根据字符统计个数直接赋分, 博文内容的情感强度计算依据的是博文内容中所表达的正面和负面情感词汇统计, 采用中国科学院计算机所软件室编写的中文分词工具ICTCLAS^[11], 对所有微博内容进行情感词汇统计. 一般情感强度定义公式可由式(1)表示:

$E = \sum {{\omega _i}{e_{\rm pos}}} + \sum {{\omega _j}{e_{\rm neg}}} $

(1)

其中, E为情感强度得分, e_pos为正面得分, e_neg为负面得分, ω为权重系数, 可以按照副词的强弱程度分类^[12].

2.2 因子分析

由于各特征信息所携带的信息量对舆情热度预测的贡献率以及关联度差异较大, 从而会影响最终的预测结果, 同时信息中的噪声和冗余也会影响预测结果的精度. 因子分析采用潜在的假想变量和随机影响变量的线性组合表示原始变量, 通过提取其中具有较高贡献率的因子来进行预测分析, 既能反映舆情热度的真实情况, 又可以过滤影响结果的冗余信息, 从而提高预测精度^[13].

首先根据所采集到的特征信息, 可视为随机特征向量 $x = {({x_1},{x_2}, \cdots ,{x_n})^{\rm{T}}}$ ,其均值为 $\;\mu = {({\mu _1},{\mu _2}, \cdots ,{\mu _n})^{\rm{T}}}$ , 协差阵为 $S = {\sigma _{ij}}$ , 因子分析的模型如下表示:

$ \left\{\begin{array}{c}{x}_{1}={\mu }_{1}+{a}_{11}{f}_{1}+{a}_{12}{f}_{2}+\cdots +{a}_{1m}{f}_{m}+{\varepsilon }_{1}\\ {x}_{2}={\mu }_{2}+{a}_{21}{f}_{1}+{a}_{22}{f}_{2}+\cdots +{a}_{2m}{f}_{m}+{\varepsilon }_{2}\\ \vdots \\ {x}_{n}={\mu }_{n}+{a}_{n1}{f}_{1}+{a}_{n2}{f}_{2}+\cdots +{a}_{nm}{f}_{m}+{\varepsilon }_{n}\end{array}\right. $

(2)

其中, ${f_1},{f_2}, \cdots ,{f_n}$ 为公共因子, ${\varepsilon _1},{\varepsilon _2}, \cdots ,{\varepsilon _n}$ 为特殊因子, 彼此都不相关, 每个因子只对当前原始变量起作用, 用矩阵形式表示为:

$ {{x = \mu + Af + \varepsilon }} $

(3)

其中, A为因子荷载矩阵. 然后采用主成分法进行参数估计, 通过求解其特征根 ${\hat \lambda _i}\left( {{{i}} = 1,2, \cdots ,n} \right)$ 和相应的正交单位特征向量为 ${\hat t_i}\left( {{{i}} = 1,2, \cdots ,n} \right)$ , 选取保留较多原始信息的因子数m, 计算其贡献率G.

$ G = \sum\nolimits_{i = 1}^m {\hat \lambda } \Bigg/\sum\nolimits_{i = 1}^n {\hat \lambda } $

(4)

当贡献率G达到一个较高的百分比, 协差阵为S可作如下的近似分解:

$\begin{array}{l} S = \left( {{{\hat t}_1} \cdots {{\hat t}_p}} \right)\left( {\begin{array}{*{20}{c}} {{{\hat \lambda }_1}}&{}&{} \\ {}& \ddots &{} \\ {}&{}&{{{\hat \lambda }_n}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\hat t_{_1}^{\rm{T}}} \\ {\vdots} \\ {\hat t_n^{\rm{T}}} \end{array}} \right) \\ \quad \approx {{\hat \lambda }_1}{{\hat t}_1}\hat t_{_1}^{\rm{T}} + \cdots + {{\hat \lambda }_m}{{\hat t}_m}\hat t_m^{\rm{T}} + \hat D \\ \quad = \hat A{{\hat A}^{\rm{T}}} + \hat D \\ \end{array} $

(5)

其中,

$ \left\{ \begin{array}{l} \hat A = \left( {\sqrt {{{\hat \lambda }_1}{{\hat t}_1}} , \cdots, \sqrt {{{\hat \lambda }_m}{{\hat t}_m}} } \right) = \left( {{{\hat a}_{ij}}} \right) \\ {\hat D = diag\left( {\hat \sigma _1^2, \cdots ,\hat \sigma _n^2} \right)} \\ {\hat \sigma _1^2 = {s_{ii}} - \displaystyle\sum\nolimits_{i = 1}^m {\hat a_{ij}^2,\;i = 1, \cdots ,n} } \\ \end{array} \right. $

(6)

式中, $\hat A$ 和 $\hat D$ 就是因子模型的一个解.

为了能更清楚的了解各公共因子的物理解释意义, 采用最大方差法对因子荷载阵进行旋转, 使因子荷载阵的结构简化, 荷载矩阵中每列或行的元素平方值向0和1两极分化. 令 $\Gamma $ 为正交阵, 做正交变换求解:

$ B = {({b_{ij}})_{n \times m}} = \left( {\mathop \sum \limits_{l = 1}^m {a_{il}}{\gamma _{lj}}} \right) $

(7)

A的行元素平方和为 $h_i^2 \!\!=\!\! \displaystyle\sum\limits_{j = 1}^m {a_{ij}^2}$ , 令 ${d}_{ij}\!\!=\!\!\dfrac{{b}_{ij}}{{h}_{i}},i\!\!=\!\! \mathrm{1,2},\cdots , n;\;j=\mathrm{1,2}$ .

定义因子荷载矩阵A的方差为:

$V\left( \theta \right) = \displaystyle\sum\limits_{j = 1}^m {\dfrac{{\displaystyle\sum\nolimits_{i = 1}^p {{{\left( {d_{ij}^2 - {{\bar d}_j}} \right)}^2}} }}{p}} $

(8)

最后, 采用回归的方法将式(3)转化为:

$ {F}_{j}={\beta }_{j1}{X}_{1}+\cdots +{\beta }_{jn}{X}_{n},\;j=1,\cdots ,m $

(9)

其中, $\;\beta $ 为因子的得分系数, F为各因子的最终得分. 利用提取的公因子进行预测分析不仅达到了降维的目的, 而且每个因子都具备物理解释意义, 更有利于舆情热度影响因素的分析.

2.3 Elman网络 2.3.1 Elman网络结构设计

Elman模型结构中不仅包含输入层、中间层(即隐含层)和输出层, 还包含记载中间层历史信息的承接层^[14], 相较于一般静态神经网络具有动态特性好, 逼近速度快等特点. 当然, Elman网络自身缺少对输入输出层的反馈而忽略了其对最终结果的影响^[15], 可以通过增加神经元个数, 利用所有层的历史信息来反馈调节模型预测结果, 其网络结构如图1所示.

标准Elman网络非线性状态空间表达式为^[16]:

${{x}}\left( k \right) = f\left( {{\omega _1}{{{x}}_c}\left( k \right) + {\omega _2}{{u}}\left( {k - 1} \right)} \right)$

(10)

$ {{y}}\left(k\right)=g\left({\omega }_{3}{ }{{x}}\left(k\right)\right)$

(11)

$ {{{x}}}_{c}\left(k\right)={ }{{x}}\left(k-1\right)$

(12)

其中, ${{\omega }}$ 为各层连接权值矩阵, $f\left( {\rm{*}} \right)$ 为中间层传递函数, $g\left( {\rm{*}} \right)$ 为输出层传递函数. 增加神经元后, 其改进结构状态空间表达式为:

${{x}}\left( k \right) = f\left( {{\omega _2}{{u}}\left( {k - 1} \right) + {\omega _3}{{x}}\left( k \right) + {\omega _4}{{{u}}_c}\left( {k - 1} \right) + {\omega _5}{{{y}}_c}\left( k \right)} \right)$

(13)

${{y}}\left( k \right) = g\left( {{\omega _1}{{x}}\left( k \right) + {\omega _6}{{{x}}_c}\left( k \right)} \right)$

(14)

$ {{{x}}}_{c}\left(k\right)={{x}}\left(k-1\right)+\alpha {{{x}}}_{c}\left(k-1\right)$

(15)

$ {{{u}}}_{c}\left(k\right)={ }{{u}}\left(k-1\right)+\beta {{{u}}}_{c}\left(k-1\right)$

(16)

$ {{{y}}}_{c}\left(k\right)=m{ }{{y}}\left(k-1\right)+\gamma y\left(k-1\right)$

(17)

其中, $\alpha $ 、 $\;\beta $ 、 $\gamma $ 为反馈增益因子.

2.3.2 GA_Elman算法设计

虽然通过改进Elman网络结构可以充分利用中间层信息对预测模型进行反馈调节, 但也由此增加了网络参数数量, 其预测结果更容易受到网络权值和初始参数的影响, 而且Elman网络采用的梯度下降算法容易陷入局部最优解^[17]. 借助遗传算法理论上可以扩大到整个解空间范围来寻找最优解. 由于遗传算法中每个种群个体都包含了Elman网络的所有权值和参数, 个体通过适应度函数计算适应度值, 通过选择合适的种群规模并利用迭代的方式进行选择、交叉和变异等运算就可以找到其最优适应度对应的个体, 即最优权值参数. GA_Elman算法的主要训练流程如图2所示.

根据2.3.1节中式(13)~式(17), 可知遗传算法需要对6个网络权值矩阵和3个反馈增益因子进行训练计算, 将预测输出和期望输出误差绝对值的倒数作为适应度函数, 计算公式为:

$fit = \frac{1}{{k\left( {\displaystyle\sum\nolimits_{i = 1}^n {{\rm{abs}}(E\left( {{y_i}} \right) - {y_i}} } \right)}}$

(19)

其中, n为网络输出节点数, ${y_i}$ 为第i个节点预测输入, $E\left( {{y_i}} \right)$ 为第i个节点期望输出, k为样本系数. 式(19)中选择误差的绝对值和没有采用误差平方主要是为了筛除种群中适应度受到输入数据中离群点和异常值影响的个体. 此外, 染色体选择方法采用轮盘赌法, 即基于适应度比例的选择策略^[18].

3 实验分析 3.1 实验数据处理

本实验由课题小组基于Python语言开发的爬虫工具来获取新浪公开发布的微博数据, 以2020年热度始终在持续的“疫情”为关键词, 爬取从2020年1月21日至2020年4月27日的每天热门微博作为实验数据, 共采集到67238条数据. 按照2.1节特征量化的方式对数据进行预处理, 以日期为标签可汇总成98组数据, 每组数据可提取13个可量化特征.

由于新浪微博仅对博主自身开放微博“浏览量”这一热度数据, 无法从公开数据中采集到, 因此本文分别选择和舆情热度密切相关的全网“博文数”和博主的博文“点赞数”作为目标特征, 构造2个实验来对结果分析比对, 以验证方法的客观有效性, 构造方式如表2所示.

实验采用均方误差(MSE)和判定系数(R²)作为评价标准, 其公式如下所示:

$MSE = \dfrac{1}{n}\mathop \sum \limits_{i = 1}^n {\left( {{y_i} - {p_i}} \right)^2}$

(19)

${R^2} = \frac{{SSR}}{{SST}} = 1 - \frac{{SSE}}{{SST}}$

(20)

其中, ${y_i}$ 为的目标值, ${p_i}$ 的预测值, SST为总平方和, SSR为回归平方和, SSE为残差平方和.

3.2 博文数预测结果分析

根据2.2节式(2)–式(4)提取各公共因子并计算累积率, 如表3所示.

表3中显示了各主成分解释原始变量总方差的情况, 为了尽可能保留原始特征信息, 同时又达到降维去噪的目的, 经过比较实验, 选择保留前6个因子的实验效果最佳, 因篇幅有限, 分析比较的实验过程不再赘述. 由式(5)–式(9)得到旋转后的因子成分表, 如表4所示.

从表4中可比较清晰的看出各成分的物理解释意义, 成分1可以认为是博主自身的影响力因子, 成分2是平台影响因子, 成分3是微博自身热度影响因子, 成分4为受众面影响因子, 成分5为博文内容影响力因子, 成分6为微博传播持久力影响因子.

为了更好的检验预测效果, 将清洗处理后的数据随机分成两组, 前83组为训练集, 后15组为测试集, 然后分别对原始特征数据采用Elman算法预测(记为Elman), 再对提取的公因子采用Elman算法(记为FA_Elman)和改进后的Elman算法(记为FA_GA_Elman)进行预测结果比对, 实验中遗传算法的种群规模为100, 交叉概率选择为0.3, 变异概率选择为0.2, 迭代次数为500. 其结果对比如图3所示, 评价指标对比如表5所示.

从预测结果及评价指标中可以看出, 采用公因子作为训练特征其预测精度要优于直接以原始数据作为训练特征, 而改进后的Elman算法预测精度要优于标准Elman算法,而且经过遗传算法优化后的Elman网络在预测结果上要比标准Elman网络稳定许多.

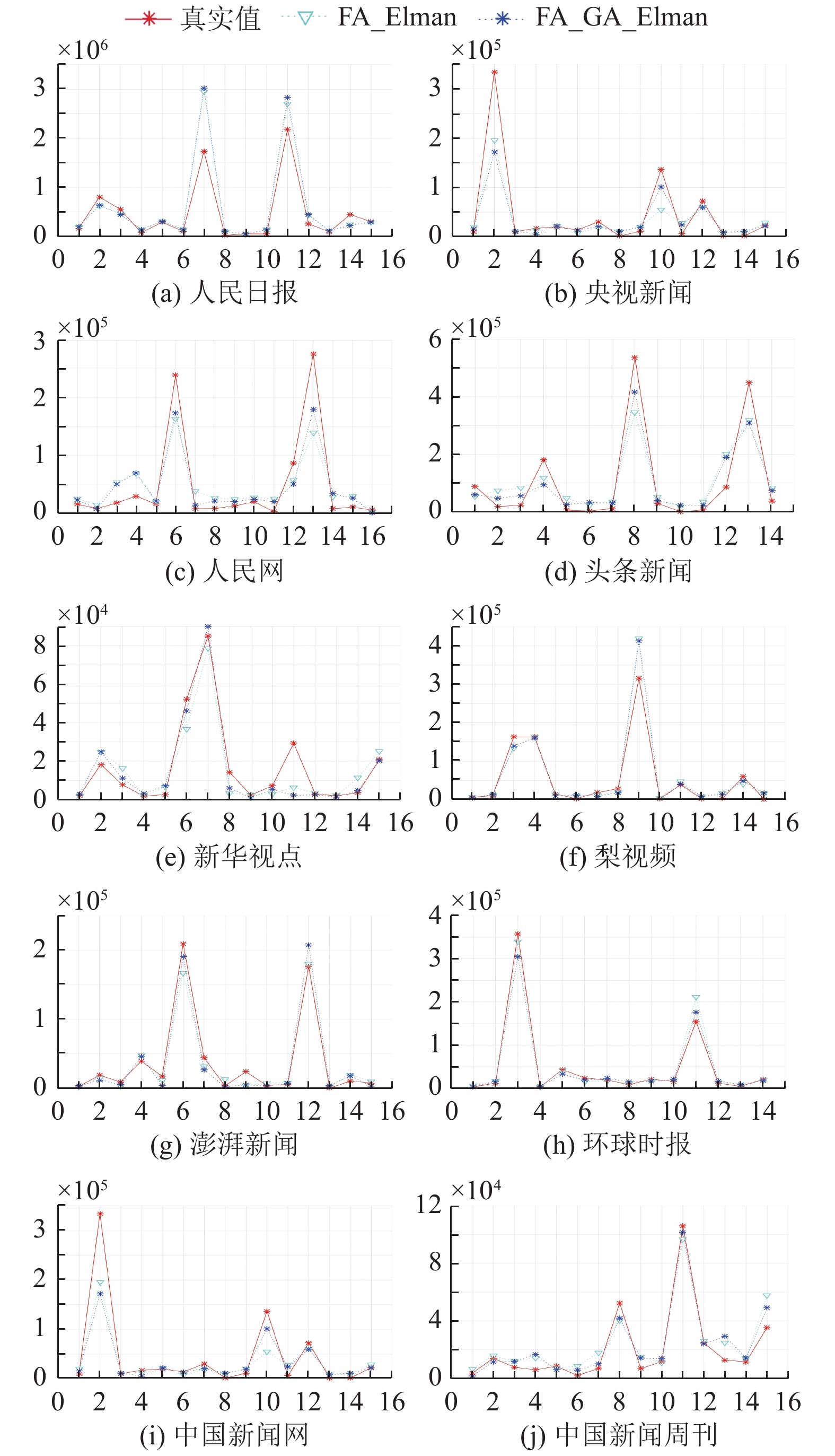
3.3 点赞数预测结果分析

为更好检验本方法对于点赞数预测的有效性, 在数据集中综合选择了拥有较多粉丝数量且周期内发博数量稳定的前十名热门博主, 对其每天点赞数量进行预测, 将FA_Elman和FA_GA_Elman预测结果进行比对. 由于各博主不一定每天发布相关微博, 统一取15组数据作为测试集, 其余数据作为训练集, 其预测结果如图4所示.

从图4中可以看出, FA_Elman和FA_GA_Elman的预测结果与真实值比较均具有较好的拟合度, 而且对于突发值也能很好地反映其真实趋势. 表6给出了评价指标的对比结果以及各因子贡献率, 从中可以看出FA_GA_Elman预测精度要优于FA_Elman, 同时也表明通过因子分析, 可以从数据集中提取出影响舆情热度的内在因子, 消除噪声干扰, 从而达到良好的预测效果. 以人民日报点赞数预测为例, 经过训练后, 其网络参数如表7所示, 优化后网络参数权值范数要小于优化前的网络参数权值, 说明优化后的网络具有更好的泛化性能.

4 结论

新时期, 网络舆情具有信息规模大, 传播速度快, 参与范围广, 实时交互强等特点, 把握舆情热度无论对企业的经营策略, 还是社会的公共安全都极为重要. 本文结合了因子分析和GA_Elman网络的特点, 提出了一种能有效预测舆情关键词热度的模型, 首先采用因子分析方法揭示数据背后影响舆情热度的真正内因, 然后通过改进Elman网络结构并利用遗传算法优化网络权值参数, 训练输出特征目标预测值. 根据不同模型的实验结果对比, 本文提出的方法能有效的预测基于关键词的舆情热度, 预测精度更高, 具备一定的应用价值. 未来将进一步扩充数据集, 以期为相关研究提供个性化的预测分析方案.