在现代化生产过程中, 由于技术工艺水平、操作不当等因素造成的精铸零件表面缺陷是很多重大安全事故的罪魁祸首, 因此识别和检测精铸零件表面缺陷是一种非常重要的产品质量控制手段.

根据某企业实际的检测要求, 需要在生产线上在线检测电机端盖的侧面裂纹缺陷, 如图1所示. 电机端盖是电动机的核心零部件, 起着支撑传动部分、确定转子与定子的相对位置、保护电机内部和导风的作用, 其质量优劣将直接影响电机的可靠运行和工作人员人身安全. 该任务的难点体现于: ① 侧面裂纹目标特征不明显、形态多变且位置不固定, 传统的机器视觉算法难以解决; ② 由于相机视野须覆盖电机端盖整个侧面, 导致待检测的裂纹目标相对整个图片很小, 属于小目标检测; ③ 在机器视觉系统中, 工业相机位置固定, 采集的图像的背景单一, 不利于深度学习数据集的构建.

机器视觉系统中运用深度学习目标识别算法, 可以解决很多传统视觉算法难以解决的问题. 田晓杰等^[1]提出了一种优化的SSD检测方法, 用DenseNet网络结构替代VGG网络结构, 从而优化了SSD检测算法对小目标的鲁棒性, 解决硅片隐裂检测问题, 但是检测速度较慢, 不能满足实时性. 马美荣等^[2]基于RetianNet设计了一个目标检测器, 在复杂背景下的检测有极佳的表现, 解决了手机主板缺陷检测的问题, 缺点是检测器对外界环境变化的适应性一般. 目前常用的算法包括Faster R-CNN^[3]、SSD^[4]、YOLO系列^[5-9]等, 其中YOLOv4是最优秀的目标检测算法之一, 其汇集了之前的众多研究成果, 达到了检测精度和效率的最佳平衡, 本文基于YOLOv4进行端盖裂纹的检测, 并从数据集构建和损失函数两个方面进行一系列改进, 使其在端盖数据集上达到更高的检测精度.

1 数据集构建 1.1 图像增强

电机端盖的侧面特征主要包括光亮带、撕裂带和裂纹, 如图2所示, 我们希望得到的零件能获得100%的光亮带, 而实际生产中由于设备缺陷, 很难得到完全的光亮带, 断面上通常容易产生撕裂带, 但企业的质检标准认为撕裂带不影响零件的使用, 只要不出现较深的裂纹, 就认为是合格产品, 这无疑增加了检测的难度. 当裂纹出现在撕裂带的时候, 特征极不明显, 势必会影响后续的检测过程. 因此本文首先通过图像增强的方式强化裂纹目标的特征.

直方图均衡化是常用的图像增强方式, 其原理是将图像的直方图按照概率分布做一个简单的稀疏拉伸, 如图3(b)所示. 但这样的结果会导致变换后的图像虽然对比度得到增强, 但是细节纹理部分缺失, 同时图片中大片暗背景被加亮很多, 而其中少量的实际需要关注的目标对比度反而没有得到改善, 如图4(a).

针对这个问题, 本文使用一种限制对比度的直方图均衡化(CHALE)算法^[10,11], 取得了较好的效果如图4(b). 算法流程如下:

(1)将原图像划分为n个大小为 x×y (本文中取13×13)的固定子块;

(2)对这n个固定子块计算灰度直方图 ${H_i}$ ;

(3)计算平均分配到每个灰度值的像素个数: ${N_{\rm avg}} = {{{N_x}{N_y}}/ {{N_{\rm gray}}}}$ 其中, ${N_x}$ 是子区域x轴方向的像素数; ${N_y}$ 是子区域y轴方向的像素数, ${N_{\rm gray}}$ 是子区域中灰度级的数量;

(4)计算剪切阈值: ${N_{\rm res}} = {N_{\rm clip}}{N_{\rm avg}}$ , ${N_{\rm clip}}$ 设的剪切倍数, 即剪切阈值为平均分配到每个灰度值的像素个数的 ${N_{\rm clip}}$ 倍;

(5)使用对应的剪切阈值对每个子块的灰度直方图H_i进行剪切, 剪切下来的像素数目重新分配到各直方图的各灰度级中;

(6)分别对剪切后的每个子区域的灰度直方图进行直方图均衡化;

(7)获取每个子块中心点的灰度值, 将该点作为参考点, 采用双线性插值的方法对图像中的每个像素进行灰度线性插值, 最终得到的直方图如图3(c)所示. 裂纹得到明显区分, 消除了周围背景的干扰, 同时不存在过度增强的问题.

1.2 图像增强

数据增强^[12,13]的目的是扩充数据集并增加输入图像的多样性, 从而使设计的目标检测模型具有更高的鲁棒性和泛化性. 端盖缺陷检测中, 由于没有公开的数据集可以利用, 且数据通过固定位置的CCD相机采集, 导致采集的图片背景单一, 通过数据增强辅助构建一个完善的数据集尤为重要.

常用的数据增强方法有3类: ① 空间变换: 尺寸变化、随机切片、旋转等; ② 像素变化: 改变饱和度、曝光量等; ③ 信息变化: 随机擦除、添加噪声等. 改变饱和度和曝光量可以模拟工业现场环境的拍摄情况, 如光源亮度衰减、光路失真和外界环境光变化等. 如图5(b)和图5(c)所示. 对图像增加信噪比为 0.98 的椒盐噪声或高斯噪声, 模拟拍摄过程中产生的噪声, 并弱化高频率特征防止模型过拟合, 如图5(d)所示.

本文除了使用这两个数据增强方法之外, 对比了Mosaic数据增强和CutMix数据增强. Mosaic是一种新的数据增强方法, 该方法在图片上随机选取一个参考点, 过该点作水平和竖直线, 将图片分为4个大小不同的部分, 依次填充4个训练图片, 如图6(a)所示. CutMix方法是将图片中随机大小的一部分区域裁剪掉, 然后随机填充训练集中的其他数据的区域像素值, 如图6(b)所示.

在第4节中, 通过实验对比了Mosaic和CutMix数据增强在电机端盖数据上的表现, Mosaic效果略好于CutMix, 我们分析是由于电机端盖数据集的特殊性造成的, 电机端盖数据是由固定位置相机采集, 图片背景相对固定, 使用Mosaic数据增强能带来的更多的背景多样性, 另外, CutMix可能会分割待检目标, 影响目标完整性.

最终结合多种数据增强方法, 构成了包含2000张图片的端盖数据集, 按6:2:2的比例划分为训练集、验证集、测试集, 并使用Colabeler工具对数据集制作标签.

2 基于改进YOLOv4的端盖裂纹识别算法 2.1 YOLOv4

YOLOv4总体上由骨干网络、颈部网络和头部网络3部分组成. 骨干网络采用CSPDarknet53, 是在YOLOv3的Darknet53基础上引进了CSPNet块思路, 包含29个卷积层, 725×725的感受野^[14,15], 27.6 M参数, 在速度和检测精度上都有一定的提升. 颈部网络采用了空间金字塔池化(Spatial Pyramid Pooling, SPP)模块和路径聚合网络(Path-Aggregation Neck, PAN). SPP用于扩宽模型的感受野, 分离出更重要的上下文信息, 同时不会导致模型推理速度的下降. PAN是一种比YOLOv3中FPN网络更好的对不同的骨干层进行参数聚合的方法, 可以为之后的头部层提供更丰富的信息. 头部网络沿用了YOLOv3中的基于锚(anchor)的头部. YOLOv4整体结构图如图7所示.

YOLOv4的主要创新点包括: ① 使用了自对抗训练(Self -Adversarial Training, SAT)进行数据增强; ② Mosaic数据增强; ③ 在跨批次归一化(Cross Batch Normal, CBN)的基础上改进得到跨最小批的归一化(Cross mini-Batch Normal, CmBN)方法; ④ 改进PAN, 把通道的连接方法从相加(Add)改为拼接(Concat); ⑤ 修改空间注意力模块(Spatial Attention Module, SAM), 从逐空间改为逐点.

除此之外, YOLOv4使用了大量改善模型的策略, 包括使用Mish激活函数、使用DropBlock正则化方法、跨阶段部分连接、改进SOTA 方法使其更适合单GPU训练、使用遗传算法寻找最优超参数等.

2.2 YOLOv4损失函数计算规则

YOLOv4中负责计算损失函数和输出结果的YOLO层是基于锚(anchor)的, YOLO层在3个尺度下进行预测, 每个尺度划分为S×S个网格(对于608×608的输入图片, S分别为19、38、76), 每个网格产生9个候选框(anchor box), 每个anchor box会经过网络预测得到相应的预测框(bounding box). 通过人工标注的目标框称为真实框(ground truth box), 每个bounding box和ground truth box包括目标的中心坐标x、y, 宽高w、h, 置信度, 以及类别(本文数据集的类别数为1), 同时每个box负责对3个anchor box进行回归, 因此在一个批次的一个尺度的计算中, 输出box的尺寸为(4+1+1)×3=18. 前向运算的过程中, 根据bounding box和ground truth box的差异来计算损失函数.

YOLOv4的损失函数分为3个部分, 置信度损失、定位损失、分类损失. Bounding box按照一定的规则被划分为正样本、负样本和忽略样本, 对于正样本, 需要计算所有3部分损失, 对于负样本, 只需要计算置信度损失, 因为负样本不负责目标, 所以这个anchor box产生的bounding box的中心坐标、宽高、分类都属于无用信息, 也就不需要计算这部分的损失函数, 但是置信度仍然重要, 因为置信度还可以表示这个anchor box产生的bounding box中不包含对象, 所以仍然需要计算置信度损失函数. 忽略样本不需要计算损失函数.

YOLOv4对正负样本和忽略样本的划分规则和YOLOv3略有不同, 在YOLOv3中, 每个网格对应的9个anchor box中与ground truth box的IoU(交并比)最大的那一个为正样本, 负责这个目标的检测, 一个目标只对应一个正样本, 其他的anchor box如果和ground truth box的IoU大于一个阈值(Ignore_Thresh), 则为忽略样本, 否则为负样本. 而在YOLOv4中, 每个目标可以对应多个正样本, 只要IoU大于设定的阈值(IoU_Thresh, 默认值为0.213)就作为正样本, 如果都小于阈值, IoU最大的为正样本. 这个改进在一定程度上减小了YOLOv3中正负样本不平衡的问题, 是YOLOv4权衡COCO数据集中80个类别后的解决策略, 但在本文中的单类检测+小目标检测问题中, 待检测的裂纹目标相对整幅图片很小, 大部分anchor box是不包含待检测物体的, 这样会导致负样本的贡献会远大于正样本的贡献, 即没有目标的计算部分贡献会大于有目标的计算部分, 从而网络会倾向于预测单元格不含有物体, 导致平均精度偏低. 下面本文通过改进损失的计算, 来解决这种不平衡的问题.

2.3 改进YOLOv4损失函数

YOLOv4的置信度损失:

$\begin{split} Los{s_{\rm conf}} \!=\!& - \displaystyle\sum\limits_{i = 0}^{{S^2}} {\displaystyle\sum\limits_{j = 0}^B {I_{ij}^{\rm obj}} } \left[ {\hat C_i^j\log \left( {C_i^j} \right) \!+\! \left( {1 \!-\! \hat C_i^j} \right)\log \left( {1 \!-\! C_i^j} \right)} \right] \\ & - \displaystyle\sum\limits_{i = 0}^{{S^2}} {\displaystyle\sum\limits_{j = 0}^B {I_{ij}^{\rm noobj}} } \left[ {\hat C_i^j\log \left( {C_i^j} \right) \!+\! \left( {1 \!-\! \hat C_i^j} \right)\log \left( {1 \!-\! C_i^j} \right)} \right] \\ \end{split} $

(1)

其中, S表示网格数, 每个尺度上的特征图划分为S²个网格, B表示每个网格产生的anchor box的个数, $I_{ij}^{\rm obj}$ 和 $I_{ij}^{\rm noobj}$ 表示是否为正负样本, 对于正样本, $I_{ij}^{\rm obj}$ 为1, $I_{ij}^{\rm noobj}$ 为0, 对于负样本, $I_{ij}^{\rm obj}$ 为0, $I_{ij}^{\rm noobj}$ 为1, $\hat C_i^j$ 表示该样本真实置信度, 取值为0或1, $C_i^j$ 表示该样本预测置信度.

考虑到在端盖数据集中出现的正负样本严重不平衡问题, 本文引进焦点损失^[16]的思想, 在原YOLOv4置信度损失函数的基础上, 设置样本平衡系数和调制系数. 首先于正样本置信度损失前增加样本平衡系数α, 于负样本置信度损失前增加系数(1−α), 当α取值在0.5到1之间时, 负样本的计算权重降低、正样本的计算权重增加, 可以起到平衡正负样本的作用. 由于只有正样本中包含物体, 通过增加正样本的计算权重, 使得模型更倾向于预测单元格中含有目标, 从而能够提高检出率. α的取值应与正负样本之间的不平衡度成正比, α越大, 负样本所占权重越低, 平衡效果越明显. 另外, 本文对正样本增加调制系数 ${\left( {1 - C_i^j} \right)^\gamma }$ , 对负样本增加调制系数 ${\left( {C_i^j} \right)^\gamma }$ , 该系数可以解决训练样本中过多简单样本导致训练的结果对困难样本识别率不高的问题. 在本文数据库中, 数据由固定相机采集, 不可避免地会产生大量单一性样本, 这种单一性会导致大量易分的简单样本, 尤其是背景中的简单负样本. 增加调制系数后以及不同的γ取值对简单样本和困难样本的计算权重影响如图8所示, 其中横坐标x为预测置信度, 对于正样本x为 $C_i^j$ , 对于负样本x为 $1{\rm{ - }}C_i^j$ , 由图可见, 预测置信度x接近1的简单样本, 增加调制系数后其loss减小很大, 而预测置信度x较低的困难样本增加系数后其loss减少较小, 这样就相当于增加了困难样本的计算权重, 从而聚焦于困难样本的学习, 提高最终的检测精度.

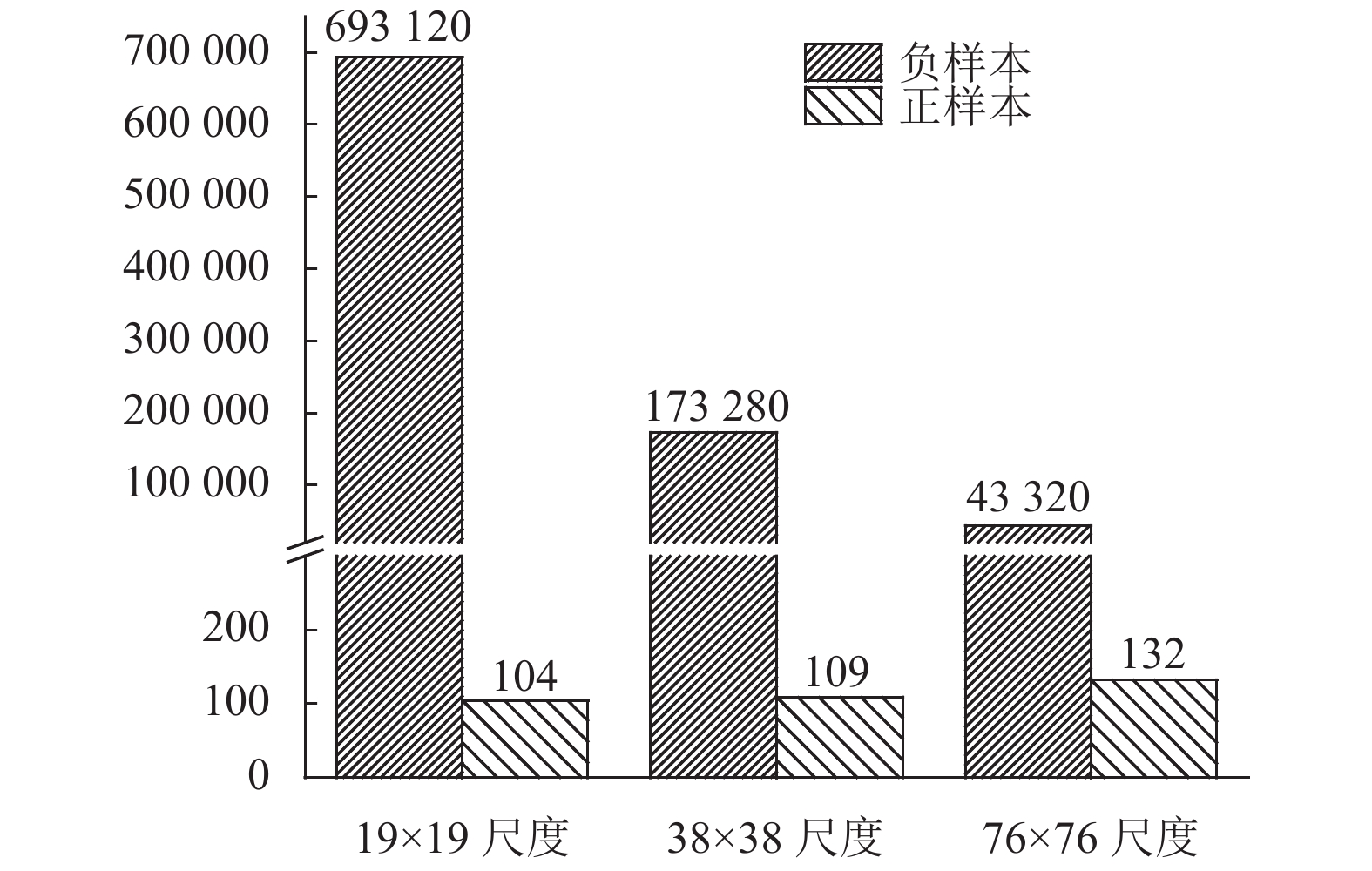
上述基于焦点损失的改进, 对置信度损失从整体上起到了调优的作用, 并得到了理论上的解释. 但在应用到端盖数据集上, 在多次调参之后, 得到的平均精度的提升依然有限, 如表1所示, 焦点损失并不能很好适配于YOLOv4. 由于YOLOv4是基于3个尺度的组合预测, 我们分别拆分19×19、38×38、76×76三个尺度, 在计算置信度损失的时候增加正负样本计数器, 在训练过程中统计80次迭代中每个尺度下的平均正负样本数, 结果如图9所示.

统计发现, 不同尺度下正负样本比不同, 如果使用相同的焦点损失系数α和γ, 对每个尺度下起到的效果并不相同, 因此, 难以得到一组最优的参数值. 由此, 本文提出了更适应YOLO的多尺度焦点损失, 以38×38尺度为参考点, 对19×19和76×76的焦点损失系数上增加不同的尺度平衡系数β, β的取值根据3个尺度下的正负样本比自适应选取, 以此来平衡不同尺度下不同的正负样本比. 最终, 得到改进后的置信度损失为:

$\begin{array}{l} Los{s_{\rm conf}} = \\ - \displaystyle\sum\limits_{i = 0}^{{S^2}} {\displaystyle\sum\limits_{j = 0}^B {I_{ij}^{\rm obj}} } \left[ {\hat C_i^j\beta \alpha {{\left( {1 \!-\! C_i^j} \right)}^\gamma }\log \left( {C_i^j} \right) \!+\! \left( {1 \!-\! \hat C_i^j} \right)\log \left( {1 \!-\! C_i^j} \right)} \right] \\ \!-\! \displaystyle\sum\limits_{i = 0}^{{S^2}} {\displaystyle\sum\limits_{j = 0}^B {I_{ij}^{\rm noobj}} } \left[ {\hat C_i^j\log \left( {C_i^j} \right) \!\!+\!\! \left( {1 \!\!-\!\! \hat C_i^j} \right)\left( {1{\rm{ \!-\! }}\beta \alpha } \right){{\left( {C_i^j} \right)}^\gamma }\log \left( {1 \!\!-\!\! C_i^j} \right)} \right] \\ \end{array} $

(2)

$\beta = \left\{ \begin{array}{*{20}{l}} {\dfrac{{{N_{\rm{2}}}}}{{3{N_1}}},}&{{{S}} = 76} \\ {1,}&{{{S}} = 38} \\ {\dfrac{{{3N_2}}}{{{N_3}}},}&{{S = 19}} \end{array} \right.$

(3)

其中, N₁、N₂、N₃为3个尺度下的正负样本比. 置信度损失在引进焦点损失策略后, 使用多尺度平衡改进和不改进在不同参数下的表现如表1所示. 改进后, 在α=0.6和γ=2的时候取得了最高的AP值, 超过了未进行多尺度改进时的最高值. 根据经验γ越大, α参的值要越小一点, 不恰当的参数可能会导致梯度爆炸, AP值为0, 表1中α=0.8和γ=1时, 改进前后AP值均为0, 即为训练失败.

YOLOv4的分类损失计算的是错误分类的损失, 计算公式如下:

$Los{s_{\rm cls}} = \sum\limits_{i = 0}^{{S^2}} {I_{ij}^{\rm obj}} \sum\limits_{c \in {\rm{classes}}} {\left( {\left[ {\hat P_i^j\log \left( {P_i^j} \right) + \left( {1 - \hat P_i^j} \right)\log \left( {1 - P_i^j} \right)} \right]} \right.} $

(4)

其中, $\hat P_i^j$ 表示真实类别, $P_i^j$ 表示预测类别概率值. 本文中数据集只有一个类别, 因此不对分类损失的计算做过多的优化.

YOLOv4的定位损失包括中心坐标损失、宽高损失. IoU损失是目标检测广泛使用的定位损失, 计算公式如下:

$Los{s_{\rm IoU}} = 1 - R_{\rm IoU}{\rm{ = 1}} - \frac{{\left| {B \cap {B^{\rm gt}}} \right|}}{{\left| {B \cup {B^{\rm gt}}} \right|}}$

(5)

其中, B为预测框, ${B^{gt}}$ 为真实框. 基于IoU损失的改进有很多, Rezatofighi等^[17]提出GIoU损失, 在IoU损失基础上增加了C检测框(C检测框是包含了检测框和真实框的最小矩形框), 解决了检测框和真实框没有重叠的问题. 但是当真实框和检测框之间出现包含关系的时候, GIoU和IoU效果相同. Zheng等^[18]针对这一缺点, 提出DIoU损失, 将预测框和真实框都包含进C检测框, 但是DIoU计算的不是框之间的交并, 而是计算的每个检测框之间的欧氏距离. 本文的改进算法中使用CIoU损失^[18]来计算定位损失, 在DIoU损失的基础上增加了宽高比的惩罚项, 这样预测框就会更加的符合真实框. CIoU损失的计算公式如下:

$\begin{split} Los{s_{\rm CIoU}} =& Los{s_{\rm GIoU}} + \alpha v \\ =& 1 - R_{\rm IoU} + \dfrac{{{\rho ^2}\left( {b,{b^{\rm gt}}} \right)}}{{{c^2}}} + \alpha v \\ \end{split}$

(6)

$v = \dfrac{4}{{{\pi ^2}}}{\left( {\arctan \dfrac{{{w^{\rm gt}}}}{{{h^{\rm gt}}}} - \arctan \dfrac{w}{h}} \right)^2}$

(7)

$\alpha = \frac{v}{{(1 - R_{\rm IoU}) + v}}$

(8)

其中, $b$ 、 ${b^{\rm gt}}$ 是 $B$ 、 ${B^{\rm gt}}$ 的中心点, $\rho $ 为欧氏距离, c为能同时覆盖 $B$ 和 ${B^{\rm gt}}$ 的最小包围框的对角线长度, w和h为预测框的宽和高, ${w^{\rm gt}}$ 和 ${h^{\rm gt}}$ 为真实框的宽和高.

最终改进后的损失函数由增加自适应多尺度焦点损失的置信度损失、使用CIoU的定位损失和默认的分类损失组成, 并通过加权系数k₁和k₂对3部分进行加权融合, 损失函数为:

$Loss = {k_1}\left( {Los{s_{\rm conf}} + Los{s_{\rm cls}}} \right) + {k_2}Los{s_{\rm CIoU}}$

(9)

本文中k₁和k₂的取值分别为1和0.07.

2.4 利用K-means算法初始化anchor box

端盖数据集中的裂纹目标多数为线状, 如果使用默认的anchor box尺寸, 可能会导致训练起始阶段由于实际目标尺寸和设定的anchor box尺寸差异过大, 损失值的下降方向偏离甚至产生梯度爆炸. 在训练之前, 使用K-means算法对标注出来的目标框做聚类, 用聚类的结果来初始化anchor box大小, 可以有效的避免上述情况, 同时可以提高模型的学习效率, 加快收敛速度, 相当于在训练之前, 为模型提供了先验知识.

YOLOv4网络中对于每个网格的预测需要9个候选框, 因此类簇个数k取9. K-means算法对初始值是比较敏感的, 对于同样的k值, 选取的初始类簇中心不同, 会影响算法的聚类效果和迭代的次数, 经验表明, 初始的类簇中心之间的相互距离越远, 聚类效果越好^[19], 以此为出发点, 本文通过以下过程选取初始的类簇中心点:

1) 在标注的数据集中随机选取一个初始框作为初始中心, 遍历数据集中所有点x, 计算它与已选择的类簇中心的距离D(x);

2) 选取D(x)最大的点作为下一个中心点, 遍历数据集中剩余点, 计算每个点与选取的最近的类簇中心的距离D(x);

3) 重复步骤2), 直到选出9个类簇中心, 将这些值作为K-means算法的初始类簇中心.

最终通过K-means算法对端盖数据集做聚类分析, 得到9个候选框大小分别为: 21×17, 41×13, 35×19, 42×16, 54×13, 48×22, 73×22, 97×19, 90×23.

3 实验与结果分析 3.1 实验环境

硬件方面, 整个电机端盖缺陷检测系统由检测线体、CCD相机、工业光源、零件工装、光学支架以及工控机组成, 如图10所示. 其中光源选用直径120 mm穹顶光源, 与相机同轴, 可以对相机视野中物体进行均匀照射. CCD相机安装于光学支架上, 搭配8 mm镜头, 垂直拍摄电机端盖侧面, 通过调整光学支架调节相机、光源与零件之间的距离, 使得相机视野覆盖整个端盖侧面, 且清晰成像.

软件方面, 环境配置如下: Intel i5 8300处理器, 16 GB内存, NVIDIA GeForce GTX 1060显卡, OpenCV版本为3.3.0, 使用Cuda8.0 和Cudnn5.1对训练过程进行加速.

网络参数配置如下: 迭代次数为10000, 初始学习率为0.002, 采用逐步递减策略^[20], 训练到一定次数后分两次减小为原学习率的10%. 动量为0.95, 权重衰减为0.005.

3.2 实验结果对比分析

使用不同改进策略后, 进行多组对比实验, 得到的检测结果如表2所示. 其中, √表示在该组实验中使用了对应策略, FCL表示使用焦点损失+CIoU的加权融合的损失函数, MFCL表示在FCL基础上增加自适应多尺度焦点损失的改进.

应用本文的改进策略后, 平均检测精度均获得了一定程度的提高. 使用CutMix数据增强或者Mosaic数据增强后获得了最大的提升, 可见, 深度学习是一种数据驱动的方法, 对于没有公开数据集可以使用的工业场景, 使用合适的数据增强方法构架一个完善的数据集是成功检测的重要环节.

使用自适应多尺度焦点损失+CIoU的加权融合的损失函数后, AP值提升了2.7%, 改进损失函数前后的损失值曲线如图11所示. 实验证明, 这样的改进, 对于本文中的小目标+单类检测的场景十分有效.

最终的识别结果如图12所示, 检测的AP值为95.8%, 单张图片检测时间为48 ms, 满足工程应用的精度和速度要求.

使用本文中数据增强后的数据集, 在不同的算法模型下的检测效果如表3所示. 从实验结果可以看出, 使用two-stage网络结构的Faster-RCNN算法检测速度较慢, 其通过RPN网络推荐候选框, 这一过程耗时较长, 难以满足工业场景应用中的实时性要求. 而one-stage算法中, 结合了多策略的YOLOv4算法达到了检测精度和速度的最佳平衡, 检测精度和速度都优于SSD算法, 而同样使用焦点损失思想的RetineNet虽然实现了较高的检测精度, 但代价是增加了检测时间. 本文通过优化损失函数和优化anchor box初始值等改进, 将YOLOv4对于小目标的检测精度进一步突破, 同时几乎没有增加检测时间, 在同类型场景下的具有一定的工程应用价值.

4 结语

本文基于改进YOLOv4算法实现了一个电机端盖裂纹缺陷检测系统, 首先针对目标特征不明显、训练数据少且背景单一的问题, 从图像增强和数据增强两个方面系统地构建端盖数据集. 之后, 本文介绍了YOLOv4网络框架并着重解释了损失函数的计算规则, 同时创造性地提出了自适应多尺度焦点损失+CIoU损失的加权融合的改进损失函数, 并从理论和实验两个方面证明了改进损失函数的有效性. 另外, 在训练之前, 针对裂纹目标多为线状的特点, 使用K-means算法初始化anchor box, 加快了收敛速度并提高了平均精度.

最终实验结果表明, 使用改进策略和改进算法后取得了95.8%的AP值, 相较于改进前提升9.7%. 不足之处在于改进算法引入了更多的参数, 参数的调优需要耗费一定的时间.