机器视觉系统可以从工作环境中采集到的图像分析处理提取信息, 并且可以对空间尺寸进行精确测量和定位, 进而反馈给机器人, 引导机器人进行抓取、装配等操作^[1-3]. 为了将视觉系统中的位姿信息转换到机器人系统中, 手眼标定是其中的重要环节, 标定精度对机器人最终定位精度有很大影响.

传统的手眼标定方法都是通过求解AX=XB方程的形式来标定^[4]. 求解方法可以分为分步法^[5-7]和整体法^[8-10]. 除了传统的方法之外, 还有其他的手眼标定方法. Ma^[11]提出一种基于主动视觉的手眼自标定方法, 通过运动平台的三次非共面平移运动求解相机与平台间的旋转关系, 然后控制运动平台进行一次非平移运动, 通过前后两次对同一标志点的重建获得相机平移量, 代入方程求解相机与平台之间的平移关系. 杨守瑞等^[12]建立了同时包含机器人参数误差和手眼关系误差的模型, 先得到手眼关系初解, 随后将初解代入误差模型, 通过球心约束同时求解机器人误差和手眼误差. 张旭等^[13]令机器人末端吸盘携带标定板, 摄像机获取平面镜中标定板的图像, 并通过3次改变平面镜的姿态求解相机到末端靶标的位姿, 然后通过辅助相机测量末端靶标到吸盘的距离, 最终获取相机到吸盘的手眼关系.

传统的求解AX=XB方程的方法比较复杂, 常常需要机器人移动数十个位置, 而一些新的方法需要其他的高精度的测量设备. 针对以上问题, 结合实际环境和需求, 本文提出一种面向Eye-to-Hand形式的新的两步法手眼标定方法. 该方法将求解手眼关系分为求解旋转关系和平移关系两步, 首先令机器人末端进行两次平移运动获取旋转关系, 其次建立了机器人运动前后各个坐标系转换关系的模型, 通过机器人末端若干次旋转运动求解平移关系, 最后通过仿真实验和实际实验证明, 该方法操作简单、快速且具有一定精度.

1 新的两步法手眼标定

在不同应用场景下的Eye-to-Hand形式的手眼标定中, 相机与机器人的相对位置关系是多变的, 而机器人末端携带标定板运动的标定方法对相机与机器人的相对位置没有较多要求, 所以本文通过机器人末端夹持标定板运动, 相机采集标定板图像的形式进行标定.

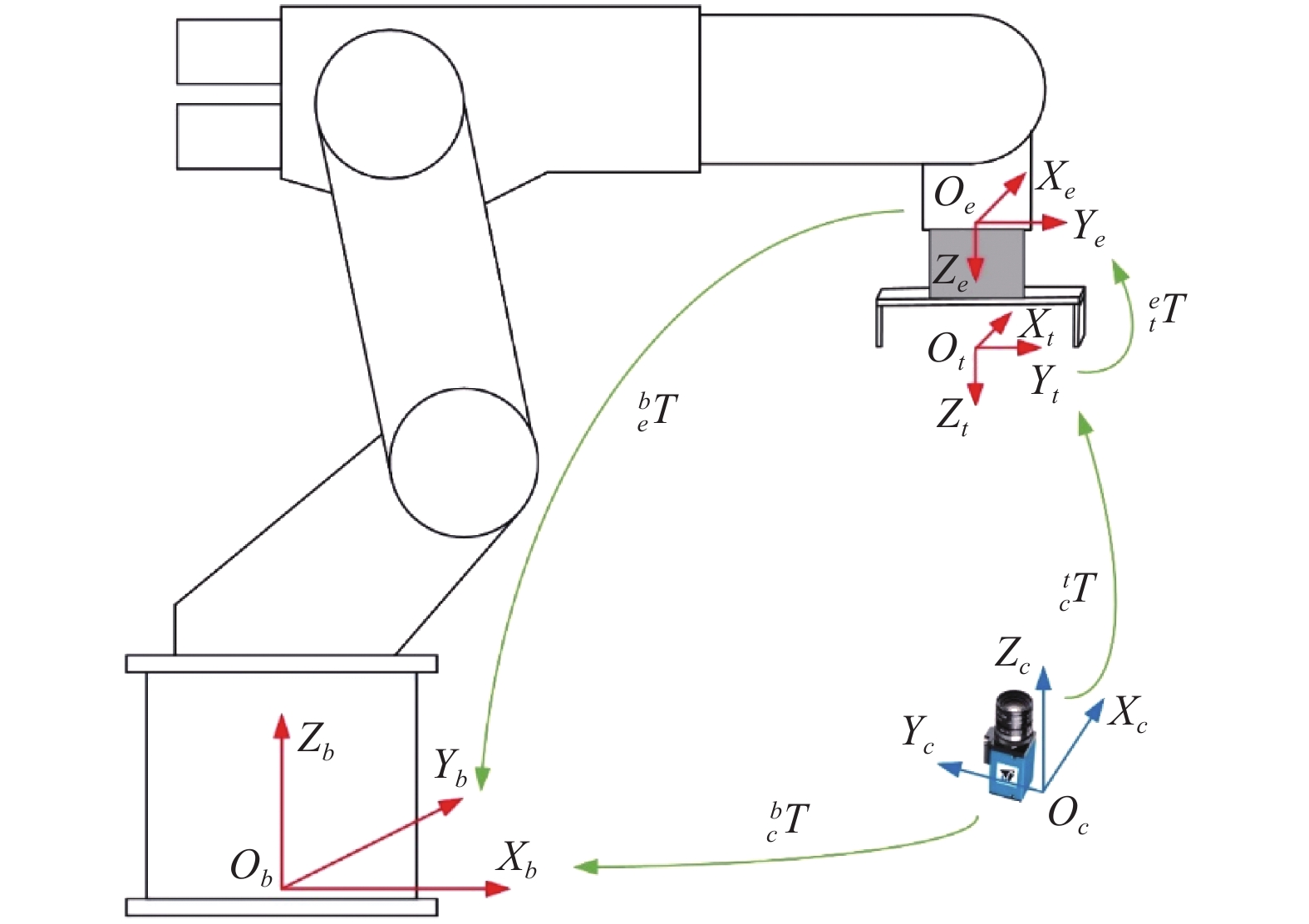
本文提出的手眼标定方法涉及到的各个坐标系如图1所示. 其中, 工具坐标系为 ${O_t} - {X_t}{Y_t}{Z_t}$ , 单目视觉系统坐标系为 ${O_c} - {X_c}{Y_c}{Z_c}$ , 机器人基座标系为 ${O_b} - {X_b}{Y_b}{Z_b}$ . 机器人每次夹持标定板到单目视觉系统上方固定点处拍照, 由于有机器人的重复定位精度保证, 可以认为每次拍照时建立在机器人末端夹爪上的工具坐标系相对于相机坐标系相对位置关系 ${}_c^t{{T}}$ 都是固定的, 因此标定出在拍照点位时的工具坐标系和相机坐标系的相对位姿, 工具坐标系与机器人基坐标系的转换关系 ${}_t^b{{T}}$ 可通过示教器读出, 也就计算出了基坐标系与相机坐标系的关系 ${}_c^b{{T}}$ .

在进行手眼标定前, 工具坐标系已由之前描述的四点法标定好, 相机也经过了单目标定获得了内参和畸变系数. 为了获取相机和工具坐标系的关系, 必须要让相机对工具坐标系上的点坐标进行测量, 由于末端夹爪上没有合作目标, 所以设计了如图2所示的编码点标定板供夹爪夹持. 设计编码点标定板坐标系为 ${O_f} - {X_f}{Y_f}{Z_f}$ , 原点建立在0号编码点圆心, X轴为0号与1号编码点圆心连线, Y轴为0号与2号编码点圆心连线, 方向在图中标出, Z轴按右手法则确定. 编码点之间的距离设置为40 mm. 在标定过程中, 单目视觉系统会对编码点标定板拍照获取编码点圆心的图像坐标, 由于编码点之间相对位置关系已知, 且获取了编码点的圆心的图像坐标, 结合相机内参, 通过求解P4P问题获取编码点在相机坐标系下的坐标.

1.1 旋转关系标定

记工具坐标系到相机坐标系的旋转矩阵为 ${}_t^{{c}}{{R}}$ . 在这里需要对两个坐标系之间的转换关系进行分析. 设两个坐标系分别为 ${O_A} - {X_A}{Y_A}{Z_A}$ 和 ${O_B} - {X_B}{Y_B}{Z_B}$ , 空间中固定点在两个坐标系之间的转换关系可表示为:

$\left[ {\begin{array}{*{20}{c}} {{x_A}}\\ {{y_A}}\\ {{{\textit{z}}_A}}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\hat{X}}_B}\cdot{{\hat{X}}_A}}&{{{\hat{Y}}_B}\cdot{{\hat{X}}_A}}&{{{\hat{Z}}_B}\cdot{{\hat{X}}_A}}&{{t_x}}\\ {{{\hat{X}}_B}\cdot{{\hat{Y}}_A}}&{{{\hat{Y}}_B}\cdot{{\hat{Y}}_A}}&{{{\hat{Z}}_B}\cdot{{\hat{Y}}_A}}&{{t_y}}\\ {{{\hat{X}}_B}\cdot{{\hat{Z}}_A}}&{{{\hat{Y}}_B}\cdot{{\hat{Z}}_A}}&{{{\hat{Z}}_B}\cdot{{\hat{Z}}_A}}&{{t_{\textit{z}}}}\\ 0&0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_B}}\\ {{y_B}}\\ {{{\textit{z}}_B}}\\ 1 \end{array}} \right] $

(1)

转换矩阵的第一列可以视为坐标系B的X轴上的单位矢量在坐标系A的X, Y, Z轴上单位矢量的投影, 第二列和第三列以此类推, 第四列为坐标系B的原点 ${O_B}$ 在坐标系A中的坐标. 所以 ${}_t^{{c}}{{R}}$ 的每一列可以看成工具坐标系主轴上的单位矢量在相机坐标系的各个轴上单位矢量的投影.

设旋转矩阵初值为 ${}_t^{{c}}{{R'}}$ , 标定步骤如下:

(1)控制机器人末端沿工具坐标系的X轴方向运动一段距离, 运动距离无需记录, 在起始点和终点处分别对标定板拍照获得标定板坐标系原点 ${O_f}$ 在相机坐标系下的坐标, 记沿工具坐标系X轴正方向计算出的坐标分别为 ${}^c{{{P}}_1}$ 和 ${}^c{{{P}}_2}$ , 通过 ${}^c{{{P}}_2} -^c{{{P}}_1}$ 之后单位化获得 ${}_t^{{c}}{{R'}}$ 的第一列 ${}^c{{\hat{X}}_t}$ ;

(2)控制机器人末端沿工具坐标系的Y轴方向运动一段距离, 后续步骤同步骤(1), 获得 ${}_t^{{c}}{{R'}}$ 的第二列 ${}^c{{\hat{Y}}_t}$ ;

(3) ${}^c{{\hat{X}}_t}$ 和 ${}^c{{\hat{Y}}_t}$ 叉乘获得 ${}_t^{{c}}{{R'}}$ 的第三列 ${}^c{{\hat{Z}}_t}$ ;

(4)由于 ${}_t^{{c}}{{R'}}$ 不是严格的旋转矩阵, 对 ${}_t^{{c}}{{R'}}$ 进行奇异值分解, 求解最接近 ${}_t^{{c}}{{R'}}$ 的旋转矩阵 ${}_t^{c}{R} = {U}{{V}^{\rm{T}}}$ .

求出 ${}_t^{{c}}{{R}}$ 后, 相机坐标系到工具坐标系的旋转矩阵 ${}_c^t{{R}} = {}_t^c{{{R}}^{ - 1}}$ .

1.2 平移关系标定

记相机坐标系到工具坐标系的平移矩阵为 ${}_c^t{{t}}$ . 平移关系可通过末端夹爪夹持标定板变换多个位姿求解出, 涉及到的坐标系较多, 转换关系如图3所示.

在固定拍照位置, 工具坐标系为 ${O_t} - {X_t}{Y_t}{Z_t}$ , 此时设置夹持在夹爪上的标定板坐标系为 ${O_d} - {X_d}{Y_d}{Z_d}$ , 工具坐标系到相机坐标系的转换关系为 ${}_t^c{{T}}$ , 工具坐标系变换位姿后, 新的工具坐标系为 ${O_{t1}} - {X_{t1}}{Y_{t1}}{Z_{t1}}$ , 相应的标定板坐标系为 ${O_{d1}} - {X_{d1}}{Y_{d1}}{Z_{d1}}$ , 工具坐标系到相机坐标系的转换关系为 ${}_{t1}^c{{T}}$ . 注意这里建立的标定板坐标系的原点为四个编码点的重心, 方向与工具坐标系的方向相同, 因此标定板坐标系与工具坐标系仅有平移关系, 而且由于在标定过程中夹爪与标定板并未相对移动, 因此标定板到工具坐标系的转换关系有:

$\left[ {\begin{array}{*{20}{c}} {{I_{3 \times 3}}}&{{}_d^t{{t}}} \\ 0&1 \end{array}} \right] = {}_d^t{{T}} = {}_{d1}^{t1}{{T}}$

(2)

${}_d^t{{t}}$ 即为标定板坐标系原点在工具坐标系下的坐标. 设编码点P在 ${O_f} - {X_f}{Y_f}{Z_f}$ 中的坐标为 ${}^f{{{P}}_i}(i = 0,1,2,3)$ , 在 ${O_c} - {X_c}{Y_c}{Z_c}$ 中坐标为 ${}^c{{{P}}_i}$ , 在 ${O_t} - {X_t}{Y_t}{Z_t}$ 中坐标为 ${}^t{{{P}}_i}$ , ${O_f} - {X_f}{Y_f}{Z_f}$ 到 ${O_c} - {X_c}{Y_c}{Z_c}$ 的旋转和平移关系分别为 ${}_f^c{{R}}$ 和 ${}_f^c{{t}}$ , 均由单目视觉系统测出, ${O_c} - {X_c}{Y_c}{Z_c}$ 到 ${O_t} - {X_t}{Y_t}{Z_t}$ 的旋转和平移关系分别为 ${}_c^t{{R}}$ 和 ${}_c^t{{t}}$ , 在这里先假设 ${}_c^t{{t}} = {{0}}$ , ${}^f{{{P}}_i}$ 到 ${}^t{{{P}}_i}$ 的转换有:

$ \left\{ {\begin{array}{*{20}{l}} {^c{{{P}}_i}{ = }_f^c{{R}}\cdot{^f}{{{P}}_i}{ + }_f^c{{t}}}\\ {^t{{{P}}_i}{ = }_c^t{{R}}\cdot{^c}{{{P}}_i}{ + }_c^t{{t}}} \end{array},\;\;{{i = 0}},{\rm{1}},{\rm{2}},{\rm{3}}} \right.$

(3)

根据之前对 ${O_d} - {X_d}{Y_d}{Z_d}$ 的定义, 可知:

${}^t{{{O}}_d} = \sum\limits_{i = 0}^3 {{}^t{{{P}}_i}} /4$

(4)

但是这里计算出的 ${}^t{{{O}}_d}$ 与真实值相差了一个 ${}_c^t{{t}}$ , 如果能标定出真实的 ${}^t{{{O}}_d}$ 也就是 ${}_d^t{{t}}$ , 就可以计算出 ${}_c^t{{t}}$ , 所以现在问题转化为求 ${}_d^t{{t}}$ .

设标定板上一点P在 ${O_{d1}} - {X_{d1}}{Y_{d1}}{Z_{d1}}$ 中坐标为 ${}^{d1}{{P}}$ , 根据图3, 该点在 ${O_c} - {X_c}{Y_c}{Z_c}$ 下的坐标^cP 可以表示为:

$\left[ {\begin{array}{*{20}{c}} {{}^c{{P}}} \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{}_{t1}^c{{R}}}&{{}_{t1}^c{{t}}} \\ {{0}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{}_{d1}^{t1}{{R}}}&{{}_{d1}^{t1}{{t}}} \\ {{0}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{}^{d1}{{P}}} \\ 1 \end{array}} \right]$

(5)

也可以表示为:

$\left[ {\begin{array}{*{20}{c}} {{}^c{{P}}} \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{}_t^c{{R}}}&{{}_t^c{{t}}} \\ {{0}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{}_d^t{{R}}}&{{}_d^t{{t}}} \\ {{0}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{}_{d1}^d{{R}}}&{{}_{d1}^d{{t}}} \\ {{0}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{}^{d1}{{P}}} \\ 1 \end{array}} \right]$

(6)

式(5)和式(6)的右边相等, 因此有:

$\begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{}_{t1}^c{{R}}}&{{}_{t1}^c{{t}}} \\ {{0}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{}_{d1}^{t1}{{R}}}&{{}_{d1}^{t1}{{t}}} \\ {{0}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{}^{d1}{{P}}} \\ 1 \end{array}} \right] \\ = \left[ {\begin{array}{*{20}{c}} {{}_t^c{{R}}}&{{}_t^c{{t}}} \\ {{0}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{}_d^t{{R}}}&{{}_d^t{{t}}} \\ {{0}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{}_{d1}^d{{R}}}&{{}_{d1}^d{{t}}} \\ {{0}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{}^{d1}{{P}}} \\ 1 \end{array}} \right] \end{array} $

(7)

结合式(2), 将式(7)展开并化简可得:

$\left\{ \begin{array}{l} {}_{t1}^c{{R}}{}_{d1}^{t1}{{R}} = {}_t^c{{R}}{}_{d1}^d{{R}} \\ \left( {{}_{t1}^c{{R}} - {}_t^c{{R}}} \right){}_d^t{{t}} = {}_t^c{{R}}{}_{d1}^d{{t}} + {}_t^c{{t}} - {}_{t1}^c{{t}} \end{array} \right.$

(8)

如果控制工具坐标系围绕TCP点只做姿态变换, 没有平移, 则 ${}_t^c{{t}} = {}_{t1}^c{{t}}$ , 式(8)中下式可进一步简化为:

$\left( {} \right) $\left( {{}_{t1}^c{{R}} - {}_t^c{{R}}} \right){}_d^t{{t}} = {}_t^c{{R}}{}_{d1}^d{{t}}$$

(9)

上式中 ${}_{d1}^d{{t}}$ 是未知量. ${}_{d1}^d{{t}}$ 可以视为 ${O_{d1}}$ 在 ${O_d} - {X_d}{Y_d}{Z_d}$ 下的坐标, 记 ${O_d}$ 和 ${O_{d1}}$ 在 ${O_t} - {X_t}{Y_t}{Z_t}$ 下的坐标为 ${}^t{{{O}}_d}$ 和 ${}^t{{{O}}_{d1}}$ , 由于 ${O_d} - {X_d}{Y_d}{Z_d}$ 和 ${O_t} - {X_t}{Y_t}{Z_t}$ 方向相同, 所以 ${}_{d1}^d{{t}} = {}^t{{{O}}_{d1}} - {}^t{{{O}}_d}$ , 根据式(3)和式(4), 最终有:

${}_{d1}^d{{t}} = \frac{1}{4}\sum\limits_{i = 0}^3 {\left( {{}_c^t{{R}}{}_{f1}^c{{R}}{}^f{{{p}}_i} + {}_c^t{{R}}{}_{f1}^c{{t}} - {}_c^t{{R}}{}_f^c{{R}}{}^f{{{p}}_i} - {}_c^t{{R}}{}_f^c{{t}}} \right)} $

(10)

上式中 ${}_{f1}^c{{R}}$ 和 ${}_{f1}^c{{t}}$ 分别为在工具坐标系变换位姿后 ${O_f} - {X_f}{Y_f}{Z_f}$ 到 ${O_c} - {X_c}{Y_c}{Z_c}$ 的旋转和平移关系, ${}_c^t{{t}}$ 在相减时已经消去, 所以之前假设 ${}_c^t{{t}}$ 为任何值不会对计算 ${}_{d1}^d{{t}}$ 造成影响.

可将式(9)视为 ${{Ax}} = {{b}}$ 的形式, 需要注意的是, ${}_{t1}^c{{R}}$ 和 ${}_t^c{{R}}$ 都是旋转矩阵, 两者作差得到的矩阵行列式为零, 如工具坐标系仅旋转一个新的位置, 仅可获得一个如式(9)的方程, 无法解出 ${}_d^t{{t}}$ . 因此, 需要将工具坐标系旋转多个位置, 求解 ${}_d^t{{t}}$ 的最小二乘解.

计算出 ${}_d^t{{t}}$ 后, 根据之前的分析, 有 ${}_c^t{{t}} = {}_d^t{{t}} - {}^t{{{O}}_d}$ , 即标定出相机坐标系到工具坐标系的平移矩阵.

设平移矩阵为 ${}_t^{{c}}{{t}}$ , 标定步骤如下:

(1)机器人夹持标定板到单目视觉系统上方固定位置处;

(2)控制工具坐标系围绕TCP点做若干次旋转运动, 并对每次位置的标定板拍照;

(3)根据式(9)和式(10)求解 ${}_d^t{{t}}$ ;

(4)最终的平移矩阵 ${}_c^t{{t}} = {}_d^t{{t}} - {}^t{{{O}}_d}$ .

2 实验验证

作为对比, 本文首先对传统的解AX=XB方程形式的手眼标定方法进行了仿真, 并且计算了标定误差. 在仿真中, 对实验数据分别设置了若干组高斯误差( $\sigma $ 从0.1至4.0), 在通过传统方法计算出手眼关系X后, 设误差 $error = \left\| {{A_i}X - X{B_i}} \right\|(i = 1,2, \cdots ,n)$ . 误差数据如表1所示, 方法1~5分别对应文献[5–9].

本文实验的硬件系统包括工业机器人、编码点标定板、工业相机及镜头. 其中, 所使用的工业机器人型号为KUKA KR60HA, 工业相机型号为德国映美精公司的DMK 33G274, 使用的镜头为Computar的M0814-MP2, 焦距8 mm. 实验环境如图4所示.

对于本文提出的新的两步法标定, 首先如2.1节所述步骤标定相机与工具坐标系的旋转关系. 标定过程采集的编码点标定板图像如图5所示.

可以看出, 标定板背景环境较为复杂, 由于采用编码点, 仍可以很好的提取圆心. 最终计算出:

${}_c^t{{R}} = \left[ {\begin{array}{*{20}{c}} {0.011\;35}&{0.9989}&{0.045\;05} \\ {0.9999}&{ - 0.011\;84}&{0.010\;65} \\ {0.011\;17}&{0.044\;92}&{ - 0.9989} \end{array}} \right]$

然后控制工具坐标系旋转不同角度, 采集各姿态下的标定板图像并记录工具坐标系在机器人基坐标系下的读数, 代入式(8)组成线性方程组, 求得 ${}_d^t{{t}} = {(10.444,} {2.8617, - 4.8581)^{\rm{T}}}$ , 与真实值相差一个 ${}_c^t{{t}}$ 的 $^t{O_d} = \left( {21.658,} \right.$ ${\left. {2.751, \!- 267.633} \right)^{\rm{T}}} $ , 最终计算 ${}_c^t{{t}} \!\!=\!\! \left( {\! - 11.214,0.1112,262.78} \right)^{\rm T}$ . 将旋转平移矩阵组合, 获得单目相机坐标系到工具坐标系的齐次变换矩阵 ${}_c^t{{T}}$ , 由示教器读出相应参数可获取 ${}_t^b{{T}} $ . 最终计算出手眼关系.

$\begin{array}{l} {}_c^b{{T}} = {}_t^b{{T}}{}_c^t{{T}} \\ = \left[ {\begin{array}{*{20}{c}} {4.39{\rm{e}} - 3}&{0.9991}&{0.042\;54}&{984.82} \\ { - 0.9999}&{4.83{\rm{e}} - 3}&{ - 0.010\;07}&{ - 341.68} \\ { - 0.010\;27}&{ - 0.042\;49}&{0.999}&{489.54} \\ 0&0&0&1 \end{array}} \right] \end{array} $

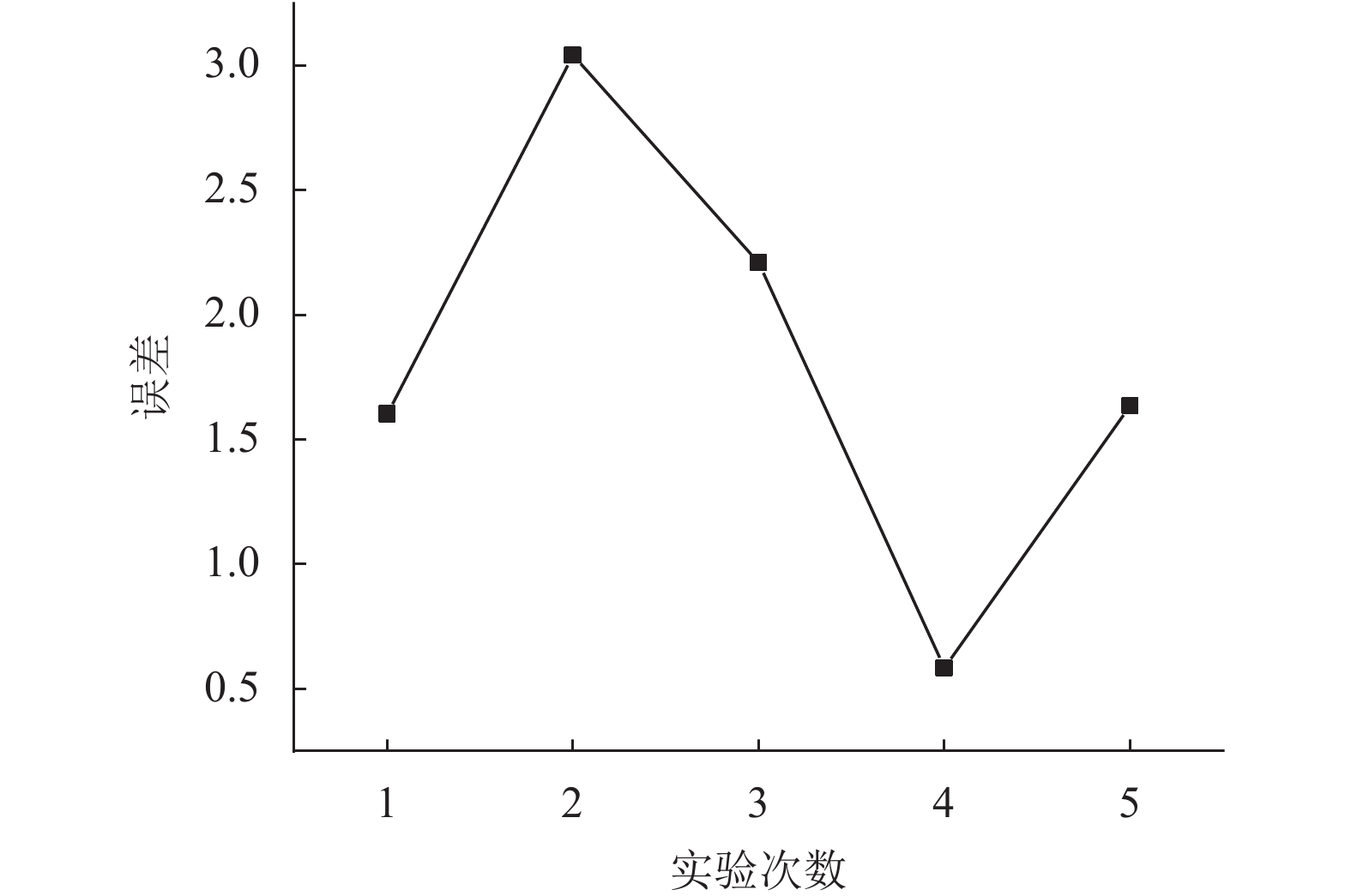
可以看出, 整个标定过程只需机器人进行两次平移运动和若干次旋转运动, 非常快速. 令机器人夹爪夹持标定板运动到不同位姿, 用单目相机采集标定板图像, 记录并计算A和B, 令 ${}_c^b{{T}}$ 作为X代入AX=XB方程, 仍然取误差 $error = \left\| {{A_i}X - X{B_i}} \right\|(i = 1,2, \cdots ,n)$ 作为精度验证. 误差数值如图6所示, 平均误差1.8148. 分析标定结果和误差可知, 本文提出的标定方法快速, 准确, 其精度优于传统方法.

3 结论

本文提出了一种新的单目视觉系统两步手眼标定方法, 该方法将标定过程分为求解旋转关系和平移关系两步, 通过控制机器人进行两次平移运动和若干次旋转运动即可计算手眼关系. 该方法与已有方法的主要区别在于其避免了对AX=XB方程的求解, 传统的基于AX=XB方程求解的方法不仅至少需要采集数十张标定板图像, 而且精度得不到保证, 本文方法不仅可以减少在标定过程中对标定板图像数量的要求, 而且实验验证了本文方法具有较高精度, 因此本文方法快速、精确, 此外该方法使用的编码点标定板非常简单, 不需要昂贵的外部设备. 在实际应用中, 机器人和环境噪声会对标定精度造成影响. 所以后续仍需要对其进行精度和标定结果优化进行大量的研究工作.