近些年, 随着信息技术和大数据产业的发展, 数据量激增, 传统集中存储设备已无法满足海量数据存储要求. 分布式存储系统(DSS)应运而生, DDS是由许多廉价磁盘组成, 具有成本低、可用性强和可扩展性高等突出优势. 它作为可存储大量数据的存储系统已经被许多互联网企业应用, 例如Microsoft和Facebook[1,2]. 然而分布式存储系统的节点易发生故障而造成数据丢失, 所以故障节点的修复成为研究的重点.
主要通过复制和编码来保证数据的可靠性. 传统的DSS多采用复制(replication)策略[3], 其中三副本最为常见. 将文件复制2次即得到3个副本, 分别将其存储到系统的不同节点. 当有节点发生故障导致数据丢失, 可以通过其他正常节点的副本进行修复. 但是其占有的存储系统开销过于庞大. 于是Dimakis提出了纠删码(erasure codes)策略[4]. 与复制策略相比, 经典的纠删码具有更大的数据可靠性和较小的存储开销. 其中最大距离可分(Maximum Distance Separable, MDS)码获得最优的存储开销性能. 但是纠删码修复故障节点时需要的修复带宽开销过大. 由于上述缺陷, Dimakis等[4]开创性的提出并介绍了再生码, 研究发现在故障节点修复时其的修复带宽开销明显降低. 但是再生码修复故障节点时需要大量有限域的运算, 计算复杂度大.
2010年Rouayheb提出了部分重复(Fractional Repetition, FR)码, FR码是一种精确最小带宽再生码, 修复故障节点时的修复带宽减小, 同时不需要大量有限域的运算, 计算复杂度较小[5,6]. 所以越来越多研究人员开始研究FR码, Ramamoorthy设计的FR码引入了组合设计的思想[7]. 相继利用二部图[8], Steiner系[9]和序列[10]构造FR码. 随后研究人员又研究了FR码的修复消耗最小化[11].
部分重复码的现有编码方式节点的存储容量基本相同, 同时重复度也基本相同, 都属于同构编码方式, 但是分布式存储系统由于设备故障, 硬件差别等原因, 导致存储成本不同, 各个节点存储容量不同, 因此需要异构编码方式. 本文提出基于Hadamard矩阵和
定义1[12]. 满足:
Hadamard矩阵具有如下性质:
(1)将Hadamard矩阵的任意两行(列)交换, 矩阵的任意一行(列)的所有元素乘−1, 得到的矩阵仍然是Hadamard矩阵.
(2) 若
本文所需的Hadamard矩阵均为标准型, 即
定义2[13]. FR码. 给定一个部分重复码
另外还需满足以下两个条件:
1)每个子集的大小为
2)
如果d和
FR码的本质为将经过MDS编码后的数据块复制
本节基于Hadamard矩阵构造存储容量不同的异构部分重复码. 首先选一个
步骤1. 首先采用
步骤2. 取一个
| $ {{{K'}}_{n + 1}} = \frac{{{{{J}}_{n{\rm{ + 1}}}}{\rm{ + }}{{{H}}_{n{\rm{ + 1}}}}}}{2} $ | (1) |
矩阵
步骤3. 将矩阵
| ${N_i} = \left\{ {j:{a_{ij}} = 1} \right\}$ | (2) |
其中,
具体的, 选取一个12阶的Hadamard矩阵如图1所示, 对其按步骤2操作得到11阶矩阵

|
图 1 12阶Hadamard矩阵 |

|
图 2 K11矩阵 |

|
图 3 K111矩阵 |
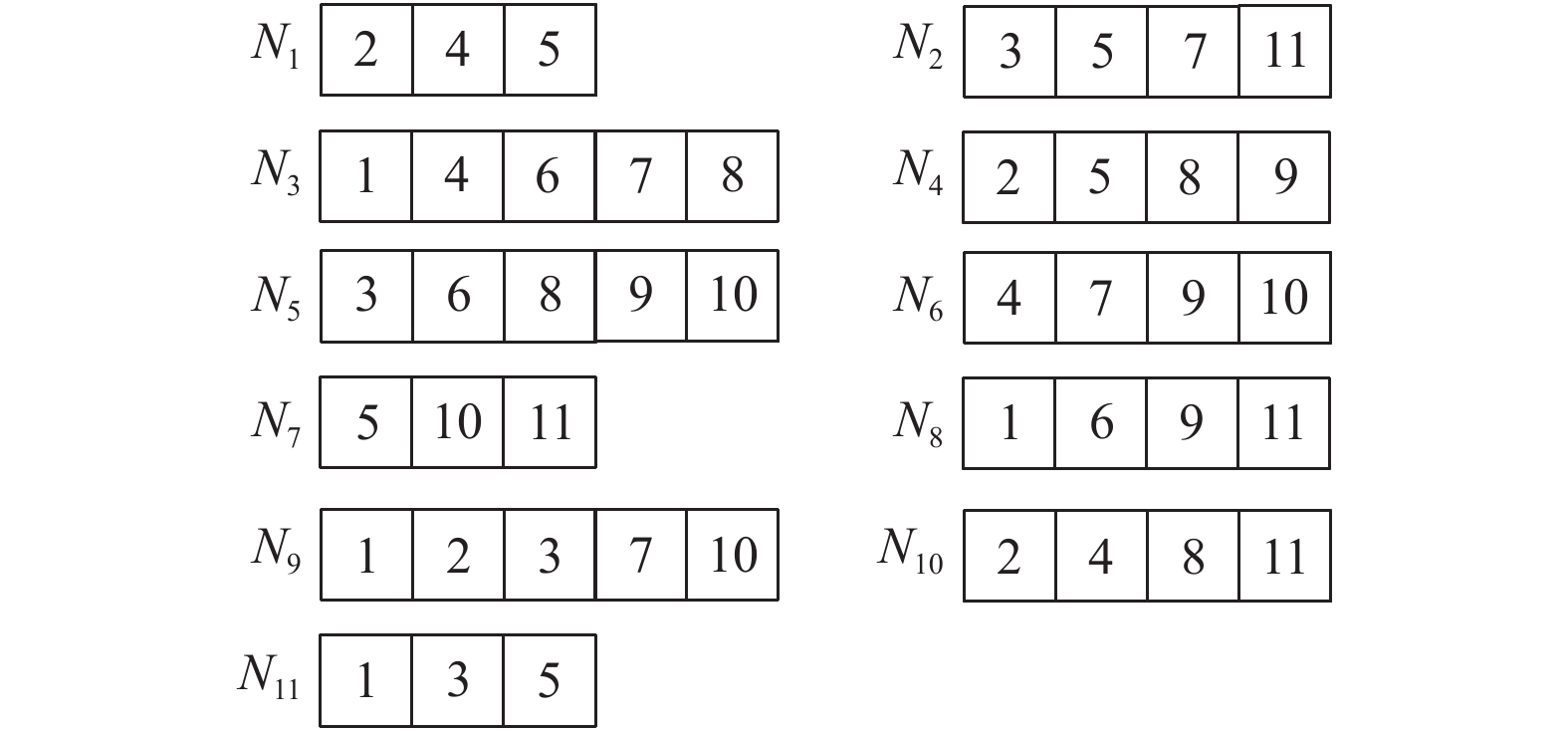
单个节点发生故障时, 可以根据存活的其他节点直接下载所需的数据, 即可恢复故障节点. 例如在图4中, 若第二个节点
|
图 4 存储容量异构的FR码节点存储结构图 |
3 可扩展的异构部分重复码
本小节提出一种基于
步骤1. 首先采用
步骤2. 取一个
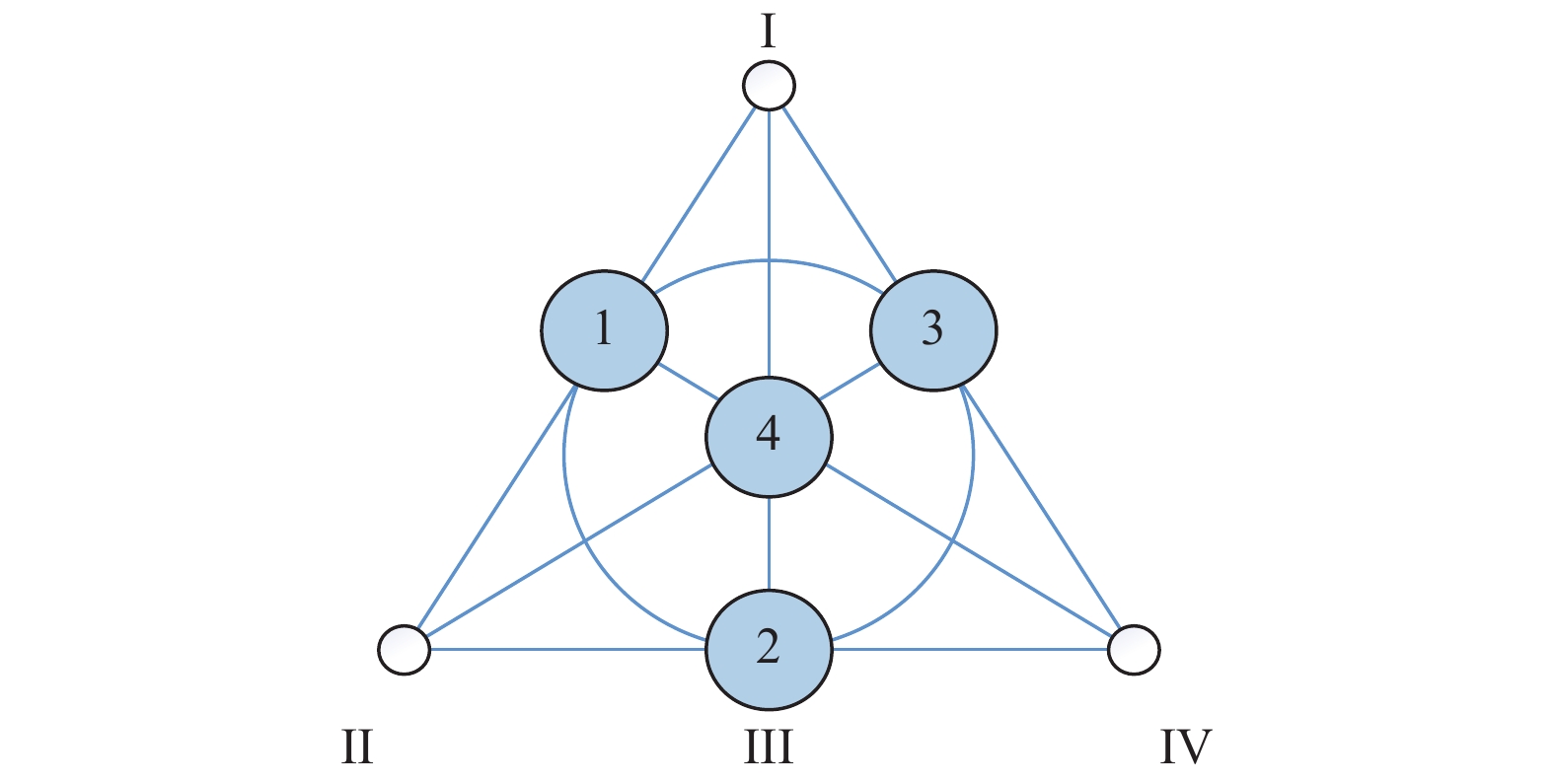
|
图 5 |
步骤3. 通过
将
步骤4. 通过将
1)将扩展的
2)当数据块
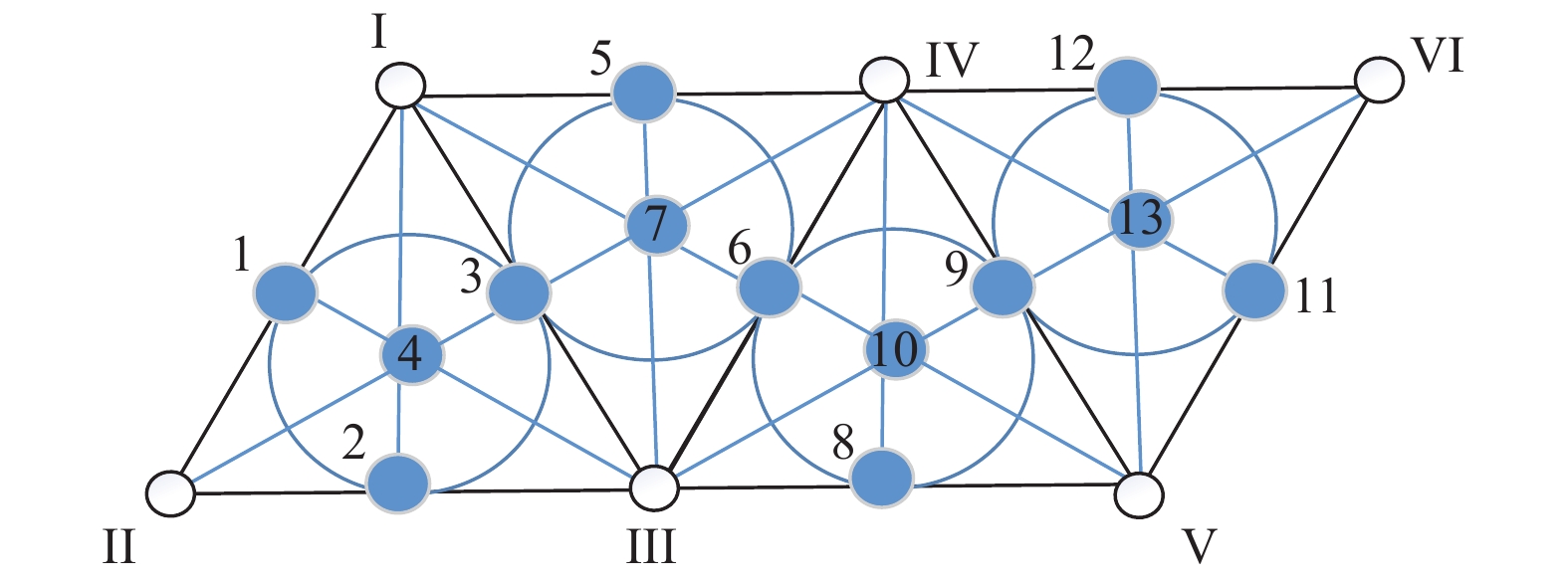
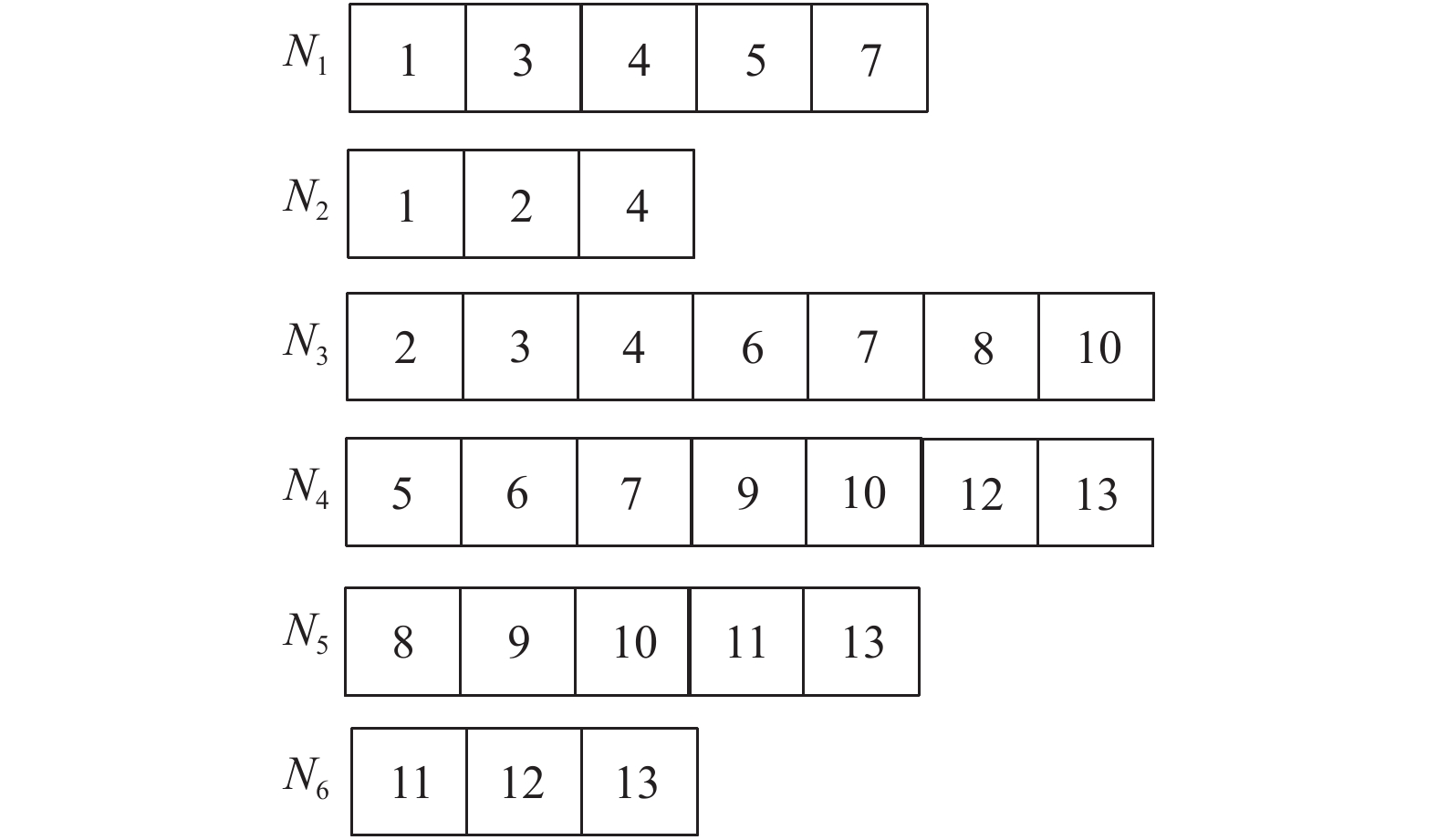
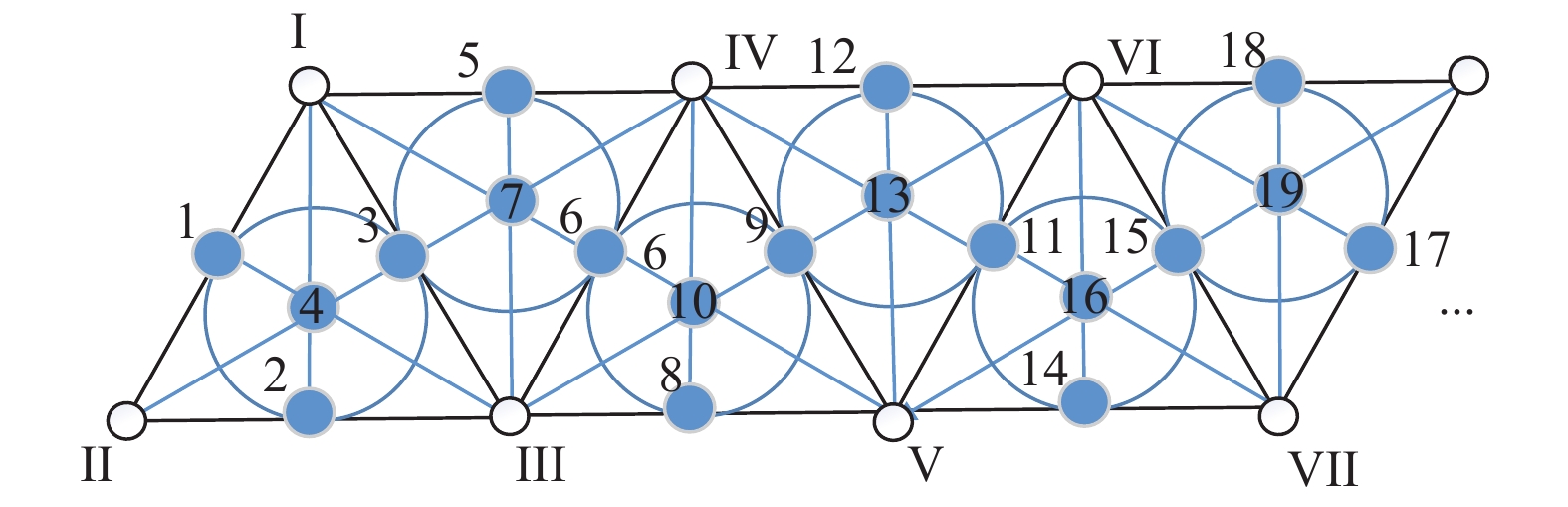
若构造一个具有6个存储节点, 13个数据块的FR码. 可将基本图形翻转拼接3次, 得到如图6所示图形, 按上述方法可得到6个存储节点所存放的数据块, 如图7所示, 若当前结构无法满足需求, 可对其进行扩展, 直至满足需求, 而且无需改变现有结构, 如图8所示.
|
图 6 图形结构 |
|
图 7 FR码节点存储结构图 |
|
图 8 扩展图形结构 |
可以看出共有6个存储节点. 存储节点N1和N5的存储容量是5, 存储节点N3和N4的存储容量是7, 并且重复度
当单个节点发生故障时, 如图7中, 当第二个节点
本小节对基于Hadamard矩阵构造存储容量异构的部分重复码和基于
修复带宽开销指的是恢复失效节点时下载的数据量大小. 例如采用
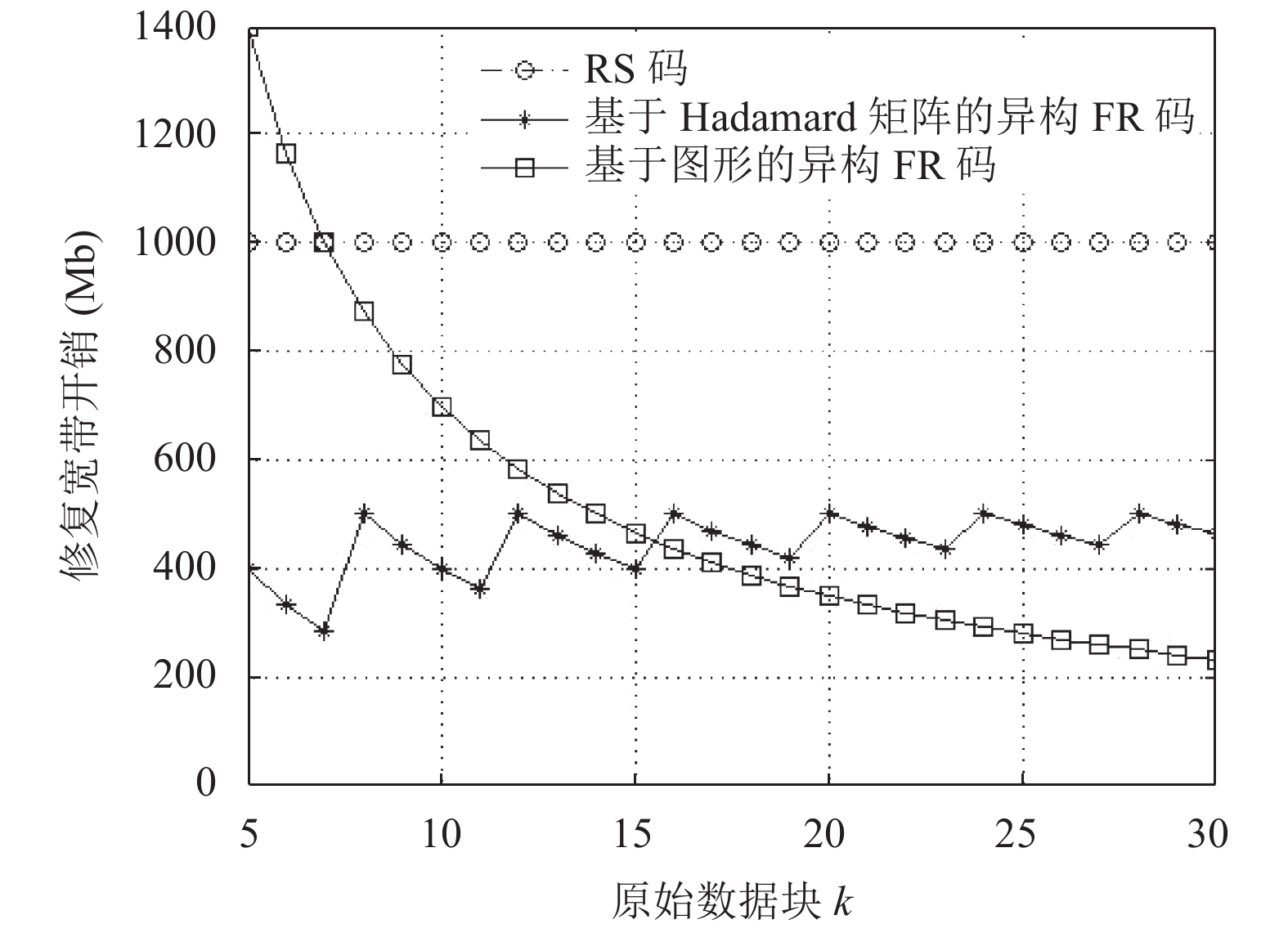
经过对比不难发现本文提出的两种异构部分重复码构造的算法, 节点发生故障时修复带宽开销比RS编码明显降低. 当节点数少于16时, 基于Hadamard矩阵构造的异构FR码修复带宽开销小于基于
发生节点故障时需要连接的存活节点数目称为修复局部性. 当发生单节点故障时,
|
图 9 修复带宽开销对比 |
采用基于
分析发现修复单个故障节点时, 基于Hadamard矩阵构造存储容量异构的FR码和基于
本文提出基于Hadamard矩阵和
| [1] |
Huang C, Simitci H, Xu YK, et al. Erasure coding in windows azure storage. Proceedings of the 2012 USENIX Conference on Annual Technical Conference. Berkeley, CA, USA. 2012. 2.
|
| [2] |
Rashmi KV, Shah NB, Gu DK, et al. A “hitchhiker’s” guide to fast and efficient data reconstruction in erasure-coded data centers. Proceedings of the 2014 ACM Conference on SIGCOMM. Chicago, IL, USA. 2014. 331–342.
|
| [3] |
Liu Y, Vlassov V. Replication in distributed storage systems: State of the art, possible directions, and open issues. 2013 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery. Beijing, China. 2013. 225–232.
|
| [4] |
Dimakis AG, Godfrey PB, Wu YN. Network coding for distributed storage systems. IEEE Transactions on Information Theory, 2010, 56(9): 4539-4551. DOI:10.1109/TIT.2010.2054295 |
| [5] |
Rouayheb SE, Ramchandran K. Fractional repetition codes for repair in distributed storage systems. Proceedings of the 48th Annual Allerton Conference on Communication, Control, and Computing. Monticello, IL, USA. 2010. 1510–1517.
|
| [6] |
王甜甜. 分布式存储系统中部分重复码构造研究[硕士学位论文]. 西安: 长安大学, 2019.
|
| [7] |
Olmez O, Ramamoorthy A. Repairable replication-based storage systems using resolvable designs. Proceedings of 2012 50th Annual Allerton Conference on Communication, Control, and Computing. Monticello, IL, USA. 2012. 1174–1181.
|
| [8] |
Koo JC, Gill JT. Scalable constructions of fractional repetition codes in distributed storage systems. 2011 49th Annual Allerton Conference on Communication, Control, and Computing (Allerton). Monticello, IL, USA. 2011. 1366–1373.
|
| [9] |
Olmez O, Ramamoorthy A. Fractional repetition codes with flexible repair from combinatorial designs. IEEE Transactions on Information Theory, 2016, 62(4): 1565-1591. DOI:10.1109/TIT.2016.2531720 |
| [10] |
Benerjee KG, Gupta MK. On dress codes with flowers. 2015 Seventh International Workshop on Signal Design and its Applications in Communications (IWSDA). Bengaluru, India. 2015. 108–112.
|
| [11] |
Itani M, Sharafeddine S, Elkabbani I. Practical single node failure recovery using fractional repetition codes in data centers. 2016 IEEE 30th International Conference on Advanced Information Networking and Applications (AINA). Crans-Montana, Switzerland. 2016. 762–768.
|
| [12] |
Banica T, Nechita I. Almost hadamard matrices: The case of arbitrary exponents. Discrete Applied Mathematics, 2013, 161(16–17): 2367-2379. |
| [13] |
Su YS. Pliable fractional repetition codes for distributed storage systems: Design and analysis. IEEE Transactions on Communications, 2018, 66(6): 2359-2375. DOI:10.1109/TCOMM.2018.2799213 |
 2021, Vol. 30
2021, Vol. 30


