基于MapReduce的程序被越来越多地应用于大型数据分析的应用中. 程序运行时间的缩短对于MapReduce程序以及所有数据处理应用而言至关重要, 而能够准确估算MapReduce程序的执行时间是优化程序的重要环节. 因此, 作者需要建立基于MapReduce程序数据处理应用的性能模型. 分析基于MapReduce程序性能模型的实验成本远低于在真实数据分析系统中设置模拟实验, 也可以得到准确的系统作业响应时间, 准确了解不同状况下的系统作业响应时间是对MapReduce作业负载管理和资源分配规划做出决策的重要依据.
基于MapReduce程序编写需要将算法调整为两阶段的处理模型, 即Map模型和Reduce模型. 以这种方式编写的程序会自动在计算集群上并行执行. Apache Hadoop是最常用的开源MapReduce模型之一. 在Hadoop1.x版本中, MapReduce程序模型与资源管理是整合在一起的. 为了达到更高的集群利用率、可靠性和可用性, 支持编程模型多样性、向后兼容性以及弹性资源模型, Hadoop2.x版本的体系结构进行了重大改进, 引入了YARN框架(Yet Another Resource Negotiator)——独立的资源管理模块. Hadoop2.x版本的体系结构发生了明显改变, YARN框架将MapReduce编程模型从资源管理结构中分离出来, 集群资源被认为是一个整体, 没有被静态地划分给每个Map和Reduce作业.
本文定义了一个在Hadoop2.x版本中能够准确估算MapReduce作业负载执行时间的性能模型. 该模型包括一个优先级树模型与一个排队网络模型, 优先级树模型可以展示一个MapReduce作业中不同任务之间的依赖关系, 排队网络模型可以展示MapReduce作业内的同步约束.
通过分析Hadoop2.x的体系结构, 作者确定了可能影响MapReduce作业执行开销的因素, 为Hadoop2.x定义了理论上的MapReduce开销模型, 该模型展示了不同MapReduce作业的优先级以及由于共享资源导致的同步延迟. 通过比较开销模型的估算数据与MapReduce的实际执行数据来评估开销模型的准确性.
1 适用于Hadoop1.x的性能评估模型有两种方法可以分析Hadoop1.x中MapReduce作业的性能, 分别为静态MapReduce性能模型和动态MapReduce性能模型. 静态MapReduce性能模型中不考虑由于争用共享资源导致的排队延迟与不同MapReduce作业之间的同步延迟. 动态MapReduce性能模型中考虑了并发MapReduce程序执行与排队延迟.
1.1 静态MapReduce性能模型静态MapReduce性能模型可以描述Hadoop1.x中MapReduce作业的执行情况. 性能模型以细粒度的方式描述MapReduce作业内各个阶段的数据流和开销情况. Map作业可分为: Read, Map, Collect, Spill、Merge五个阶段. Reduce作业的 Shuffle、Merge、Reduce、write阶段均有独立的公式. 整个工作的执行时间可以认为是Map和Reduce作业所有阶段执行时间的总和.
该模型为MapReduce作业完成时间与MapReduce作业资源分配定义上限值和下限值, 在给定的作业完成期限内分配满足该MapReduce作业所需的资源, 以便MapReduce操作在要求的期限内完成. 该框架由3个相关联的部分组成. (1)作业配置文件, 其中该应用程序Map和Reduce阶段的性能特征. (2)构建一个MapReduce性能模型, 该模型根据给定作业截止期限来估算在截止期限内完成作业所需的资源量. (3)调度程序本身, 它确定MapReduce作业顺序以及在截止日期之内完成MapReduce作业所需的资源量.
MapReduce作业完成时间与输入数据集的规模及分配资源的数量有关, 定义作业完成时间的上限TJUp, 作业完成时间下限为TJLow, 平均完成时间TJAvg. 假设TJAvg=(TJUp+TJLow)/2, 由于误差等原因, 作业平均完成时间会比作业实际完成时间少15%左右, 因此基于作业平均完成时间的预测很适合确保作业在截止日期之前完成, 是最接近实际作业完成时间的. 在Hadoop1.x中, 用于Map和Reduce作业的资源数量是预先确定的并不会更改. 在Hadoop2.x中, YARN完全将静态资源分配从MapReduce作业中分离出来, 并且不能忽略作业之间的依赖关系, 因此静态MapReduce性能模型不再适用.
1.2 动态MapReduce性能模型研究MapReduce性能模型的最大难点是, 必须精准地捕获到MapReduce作业执行过程中不同原因造成的延迟. 特别是, 属于某个MapReduce作业的任务可能会发生两种类型的延迟: 由于争用共享资源产生的排队延迟, 在同一MapReduce作业中进行协作的任务之间由于优先级约束而导致的同步延迟. 在不考虑同步延迟的条件下, 主要有两种方法可以评估并行应用程序的MapReduce作业负载性能. 第一种方法是平均值分析(MVA). MVA仅考虑任务由于共享公共资源而导致的排队延迟. 因此, MVA无法直接应用于具有优先级约束的工作负载, 例如同一个MapReduce作业中Map和Reduce任务的同步. 另一种典型的解决方案是利用马尔可夫链来表示系统的状态, 并对网络模型进行排队, 以计算系统不同状态之间的转换率. 但是, 在MapReduce作业中, 系统状态的数量会随着任务数量的增加呈指数增长, 所以此种方法无法应用于具有多个任务的MapReduce作业模型中[1].
2 Hadoop2.x的体系结构 2.1 YARN框架的构成Hadoop2.x中的最大变化就是出现了YARN框架, 它主要负责管理集群资源与作业调度. 在Hadoop1.x中, 这个功能是集成在MapReduce框架中, 由JobTracker组件实现. YARN框架的基本思想是接替JobTracker的两个主要功能, 即资源管理和任务调度/监控, 所以YARN拥有面向全局的ResourceManager和面向每一个应用程序的ApplicationMaster. 通过将资源管理与编程模型分离, YARN将集群资源认为是一个整体, 没有被静态地划分给每个Map和Reduce作业, 显著提高了集群资源利用率.
YARN模块包含3个主要组件:
(1) ResourceManager(RM): RM负责整个集群的资源管理和分配, 是一个全局的资源管理系统.
(2) NodeManager(NM): NM是每个节点上的资源和任务管理器, 它是管理这台机器的代理, 负责该节点程序的运行, 以及该节点资源的管理和监控. YARN中每个节点都运行一个NodeManager.
(3) ApplicationMaster(AM): 用户提交的每个应用程序均包含一个AM, AM负责与RM协商以获取资源(用Container表示)[2].
2.2 Hadoop2.x中的资源管理了解资源请求过程是构建Hadoop2.x性能模型的关键. 在Hadoop2.x中, AM可以以静态模式或者动态模式提出它需要的资源请求. 如果对资源的要求是在应用程序提交时确定的, 并且在AM开始运行时该资源请求没有变化, 那么可以使用静态方式请求资源. 例如在MapReduce作业中, 通过输入拆分产生的Map任务数量与通过用户定义参数产生的Reduce数量总和是固定不变的. 动态资源请求方式是指在应用程序提交时无法确定, 而需要AM根据用户指定、集群资源的可用性、业务逻辑等条件, 在运行时选择需要请求多少资源. 无论使用哪种资源请求模式, RM都不会立即分配Container给AM. AM发送分配的请求后RM最终将根据集群容量, 优先级和调度策略分配容器. 当且仅当其原始估算值发生变化并且需要其他容器时, AM才应再次向RM请求容器.
2.3 Hadoop2.x中的作业调度构建性能模型需要了解在不同节点中为任务分配容器的方式. 通过分析MapReduce的源代码Package(org.apache.hadoop.mapreduce.v2.app.rm)和JavaClass (RMContainerAllocator), 可以得到Map和Reduce任务具有不同的生命周期. Map任务的生命周期分为3个过程: Scheduled、Assigned和Completed. Reduce任务的生命周期分为4个过程: Pending、Scheduled、Assigned和Completed. 在Pending过程中, 资源请求尚未发送给RM. 在Scheduled过程, 资源请求已经发送给RM但是并未被分配. 在Assigned过程, 资源请求被分配到一个容器中. 在Completed过程, 被请求的容器已经完成执行.
此外, AM可以进行第二级的调度, 并将其获得的容器分配给作业执行计划中的任何任务. 因此, YARN中的资源分配是后期绑定. AM仅负责使用容器提供的资源, 而不会一定将该资源分配给最初请求资源的逻辑任务. 当AM接收到一个容器时, 它将使该容器与待处理任务集进行匹配, 选择一个输入数据最接近该容器的任务, 首先尝试执行本地数据任务, 然后后退到本地机架[3,4].
3 算法设计在本文中, 作者以Hadoop1.x中MapReduce作业性能模型为基础加以改进, 使它能够适应Hadoop2.x的体系结构. 需要改进方面主要有以下两处:
(1)与Hadoop1.0中为每个Map和Reduce任务预先配置资源不同, 考虑到Hadoop2.x中资源的动态分配, 需要构建一个优先级树.
(2)在Map任务和Reduce任务的Shuffle阶段因为引入管线会发生同步延迟, 需要在性能模型中及时捕获到这种延迟.
3.1 输入参数为了简单起见, 作者设计了一组数量为numNodes的计算节点, 所有计算节点都具有相同的技术特征. 工作负载由系统中同时执行的N个MapReduce作业组成. 每个作业都有mi个Map任务和ri个Reduce任务. 由于每次Shuffle操作后都会执行部分Sort操作, 所以将每对Shuffle操作与Sort操作进行分组, 形成一个单独的子任务, 这个子任务称为Shuffle-Sort任务. 在Reduce任务的最后阶段, 在完成所有的部分Sort操作后, 将执行最终Sort操作, 将最终Sort操作和Reduce函数分组到一个子任务中, 这个子任务称为Merge任务. 因此, Reduce任务分为两个子任务: Shuffle-Sort任务和Merge任务. 表1列出了性能模型的输入参数. 共有两种类型的服务资源: CPU-内存和网络. 用常量C表示任务类别的总数, 它的取值为3 (即Map任务、Shuffle-Sort任务和Merge任务).
| 表 1 输入参数表 |
3.2 改进后的均值分析(MVA)算法
作者使用了改进的均值分析算法来解决排队网络模型问题. 假设一个系统有C种任务类型和K个服务资源. 有一个向量
这个算法主要分为6个步骤, 如图1所示①~⑥.

|
图 1 改进后的均值算法的主要步骤 |
在①阶段, 初始化每个服务资源中每类任务的平均停留时间和系统中每个任务的平均响应时间. 在②阶段, 基于每个独立任务的平均响应时间构建优先级树. 在③至⑤阶段, 相同作业任务和不同作业任务在执行时间上的叠加会产生排队延迟, 考虑到排队延迟因素带来的影响, 需要重新估算任务平均响应时间. 在⑥阶段, 在新估算出的任务平均响应时间上进行融合测试. 如果融合测试失败了, 使用③至⑤阶段得到的任务响应时间, 回到②阶段重新构建优先级树, 这个优先级树会比之前构建的更加准确. 如果当前的估算值足够接近先前的估算值, 算法将结束, 由此产生最终的作业平均响应时间.
(1)初始化任务响应时间
初始化过程包含可以并发执行的两个子过程: 初始化每个服务资源中每类任务的平均停留时间和初始化系统中每个任务的平均响应时间. 要初始化任务驻留时间, 可以从相应的实际Hadoop作业执行历史中获取了驻留时间的平均值. 要初始化任务响应时间, 可以假设优先执行所有的Map任务, 然后执行Reduce任务, 于是将所有可用资源先提供给Map任务, 再提供给Reduce任务. 这种方法可以通过较少的算法迭代产生更多准确的响应时间初始化.
(2)构建优先级树
在优先级树中, 每个叶子代表一个任务, 每个内部节点都是一个运算符, 描述了任务执行过程中的约束. 使用串行(S)和并行(P)两种基本操作符号构建的优先级二叉树. 串行(S)运算符用于连接顺序执行的任务, 并行(P)运算符用于连接并发执行的任务. 优先级树的示例如图2所示.

|
图 2 优先级树示例 |
构建优先级树的主要目标是捕获作业的执行流程, 确定各个任务的执行顺序是串行还是并行, 以及各个任务之间的依赖性. 在算法的每次迭代时会重新构建优先级树, 用于重新估计任务响应时间[5].
优先级树取决于各个任务的响应时间, 使用任务响应时间线构建. 基于获得的时间线, 可以构造唯一的优先级树. 将所有同时执行的任务中耗时最长的称为一个阶段, 为了能够区分任务是顺序执行还是并发执行, 必须确定时间线中新阶段的开始点. 将时间线划分为多个阶段. 同一阶段内的所有任务并发执行, 而属于不同阶段的任务则顺序执行. 这意味着每个任务的开始或结束都会有一个新阶段开始. 时间线构造算法如算法1所示.
算法1. 时间线构造算法
输入: Map任务集合M, Reduce任务集合R, 集群节点集合N, Map任务所需的容器数m, Reduce任务所需的容器数r
输出: 时间线TL
{st: 开始时间; et: 结束时间; d: 持续时间; sd: Shuffle阶段持续时间; an: 被委派节点;}
1. 当i从1到N时, 循环执行
2. 时间线集合TL[i]为空集Ø;
3. 循环结束
4. 当m属于M时, 循环执行
5: i为TL中的最小值;
m中被委派节点m.an等于i;
m的开始时间m.st等于TL[i]中最小值;
m的结束时间m.et等于m的开始时间m.st加上m的持续时间m.d;
TL[i]等于TL[i]与{m}的并集;
6. 循环结束
7. 如果设置为slow_start, 那么
8. 边界值border等于TL[TLmin
9. 否则
10. 边界值border等于TL[TLmax]的结束时间;
11. 条件判断结束
12. 当r属于R的时候, 循环执行
13. i为TL中的最小值;
r中被委派节点r.an 等于 i;
r的开始时间r.st等于TL[i]的结束时间与边界值border中的较大值;
14. 当m属于M时, 循环执行
15. 如果m.an不等于i, 那么
16. r.d等于r.d加上m.sd除以|R|;
17. 条件判断结束
18. 循环结束
19. r的结束时间r.et等于r的开始时间r.st加上r的持续时间r.d;
20. TL[i]等于TL[i]与{r}的并集;
21. 循环结束
22. 返回值TL;
由于Map任务比Reduce任务具有更高的优先级, 算法从1~6行开始为Map任务分配容器. 如果设置为slow_start时, 则Reduce任务Shuffle阶段的开始将与占用率最低的节点上的第一个Map任务的结束重合. 因此, Shuffle阶段尽将会可能早地开始. 如果没有设置为slow_start时, Reduce任务的Shuffle阶段将会尽可能晚地开始, 如同算法的第7~11行. 算法在第12~21行为Reduce任务分发了容器.
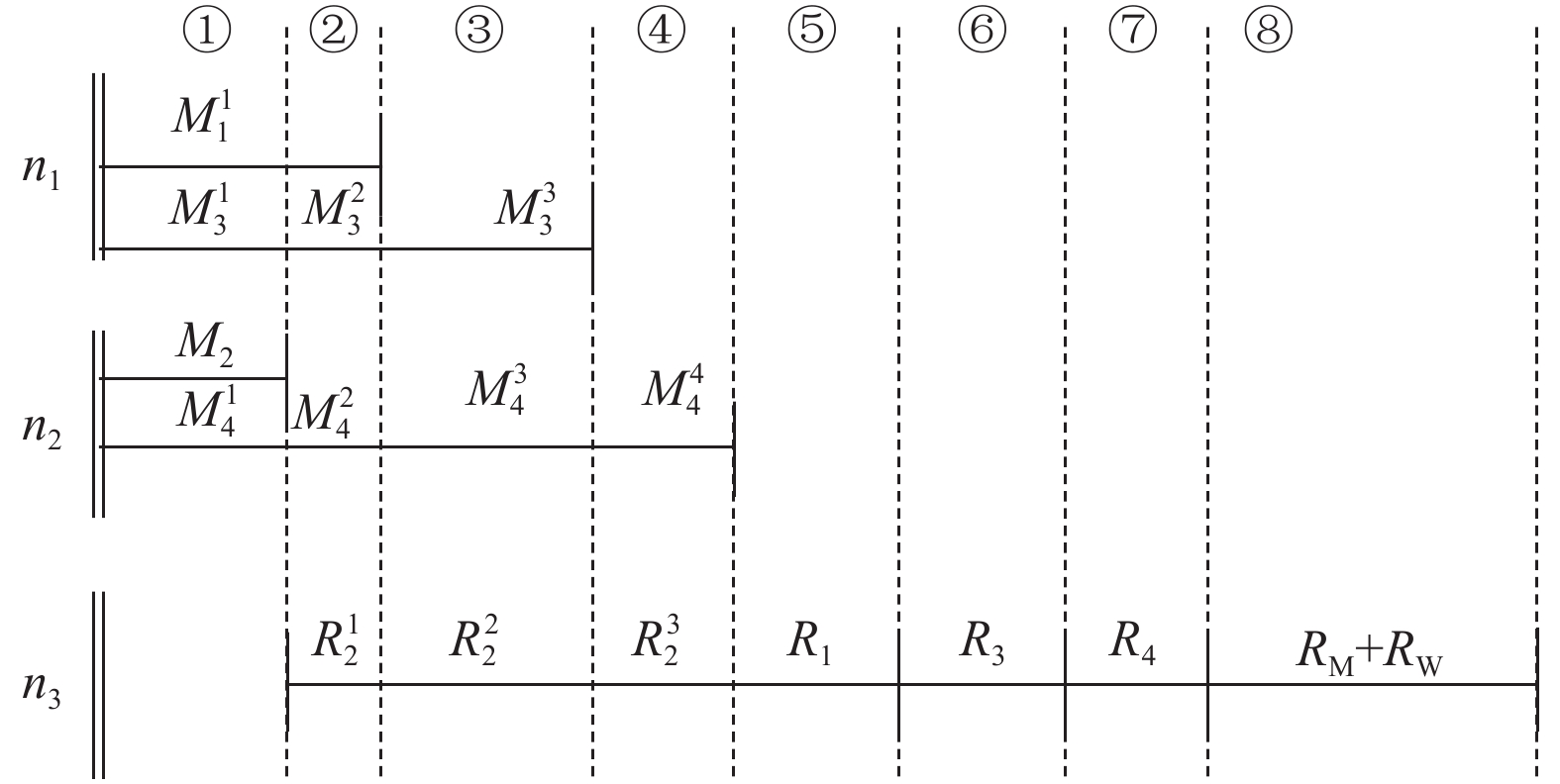
得到时间线后, 可以基于时间线构建一个二进制优先级树, 为了减少二进制优先级树的最大深度对其每一个P子树应用平衡处理. 时间线与优先级树分别如图3和图4所示.
|
图 3 时间线 |

|
图 4 优先级树 |
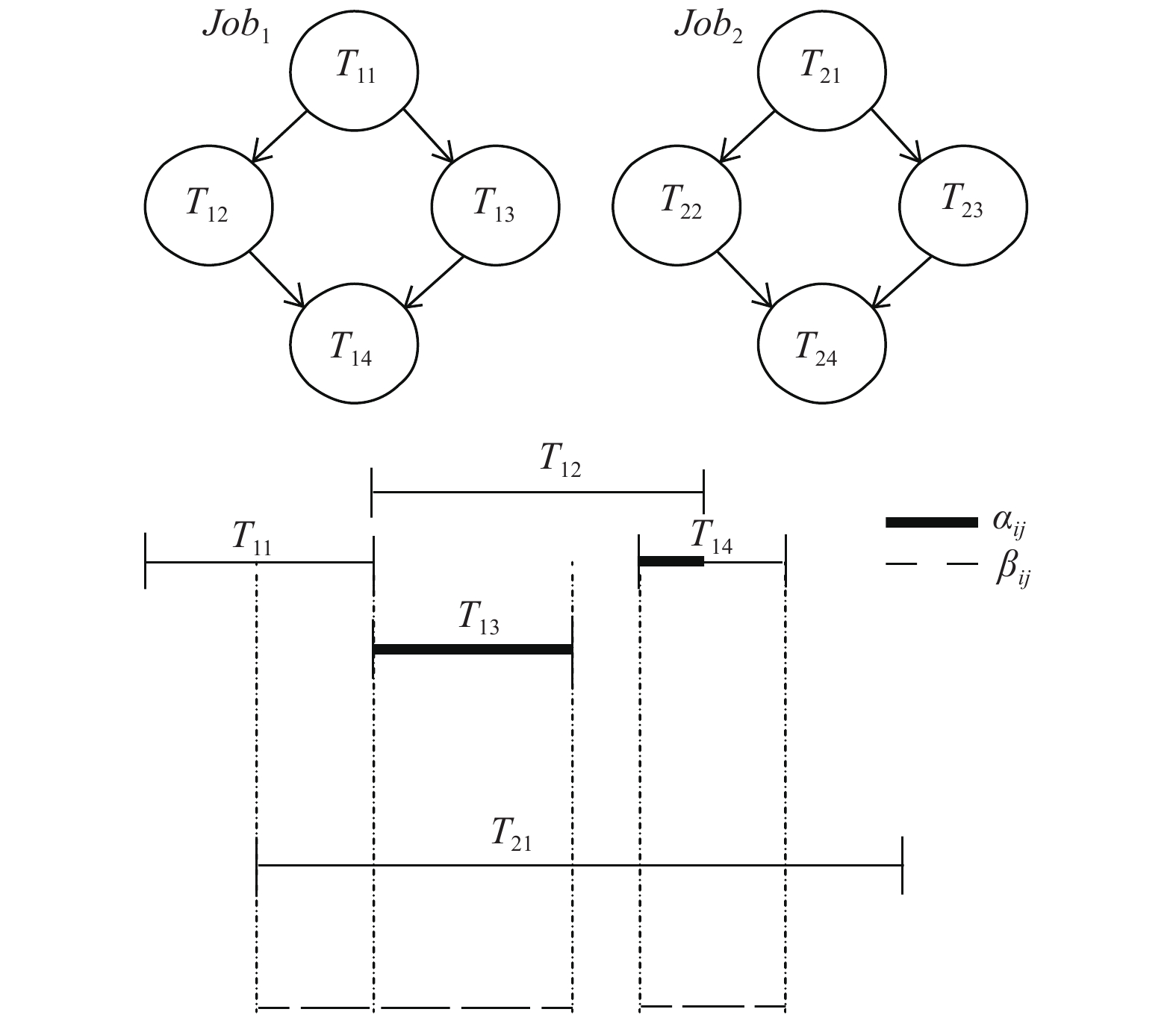
(3)计算作业内与作业间重叠因子
对于具有多个任务类型的系统, 由于j类任务所导致i类任务的排队延迟与它们的重叠成正比. 主要有两种类型的重叠因子: 作业内重叠因子
(4)计算平均作业响应时间
使用基于Fork/Join框架的算法来估算作业响应时间, 将并行阶段的作业执行看作Fork/Join块, 估算Fork/Join的平均响应时间为k个任务中平均响应时间的最大值与第k次调和函数的乘积. 公式如下:
| $ R_{ik} = H_k\cdot \max\left( {T_i,T_j} \right) $ | (1) |
其中, Hk=∑si=1/i, s为优先级树子节点的数量.
优先级树是一个二进制树, 所以Hk=3/2,
|
图 5 工作内和工作间重叠因素 |
(5)融合测试
在融合测试阶段, 比较前一次迭代产生的总响应时间总值与当前计算产生的响应时间总值, 当二者足够接近时(例如Rcurr-Rprev<10−7), 算法执行完毕. 否则, 算法将返回到优先级树构建阶段重新执行. 经试验测试, 将差值标准定为10−7, 可在精度级别和算法复杂性(迭代次数)之间提供良好的折衷方案. 当这个差值值较低时, 计算出的作业响应时间几乎不再改变, 但是算法迭代次数会继续增长[7].
4 实验 4.1 试验设置实验中使用基于Fork/Join框架的模型与Hadoop1.x原生方法的测量结果进行比较. 设计一组实验参数, 在Map-Reduce任务中输入大量作业(例如word-count程序), 输入数据经过处理会生成大量中间数据用来分析作业响应时间. 分析每个实验中固定3个参数中两个参数的工作响应时间, 每个实验重复5次, 然后取响应时间的中位数.
实验参数如下:
(1) 节点数量: 4个, 6个, 8个.
(2) 输入数据量: 1 GB, 5 GB.
(3) 集群中同时执行的任务数量: 1~4个.
(4) 集群中每个节点的配置相同: XeonE5-2630@2.4 GHz/128 GB /1 TB /4 GiEthernet.
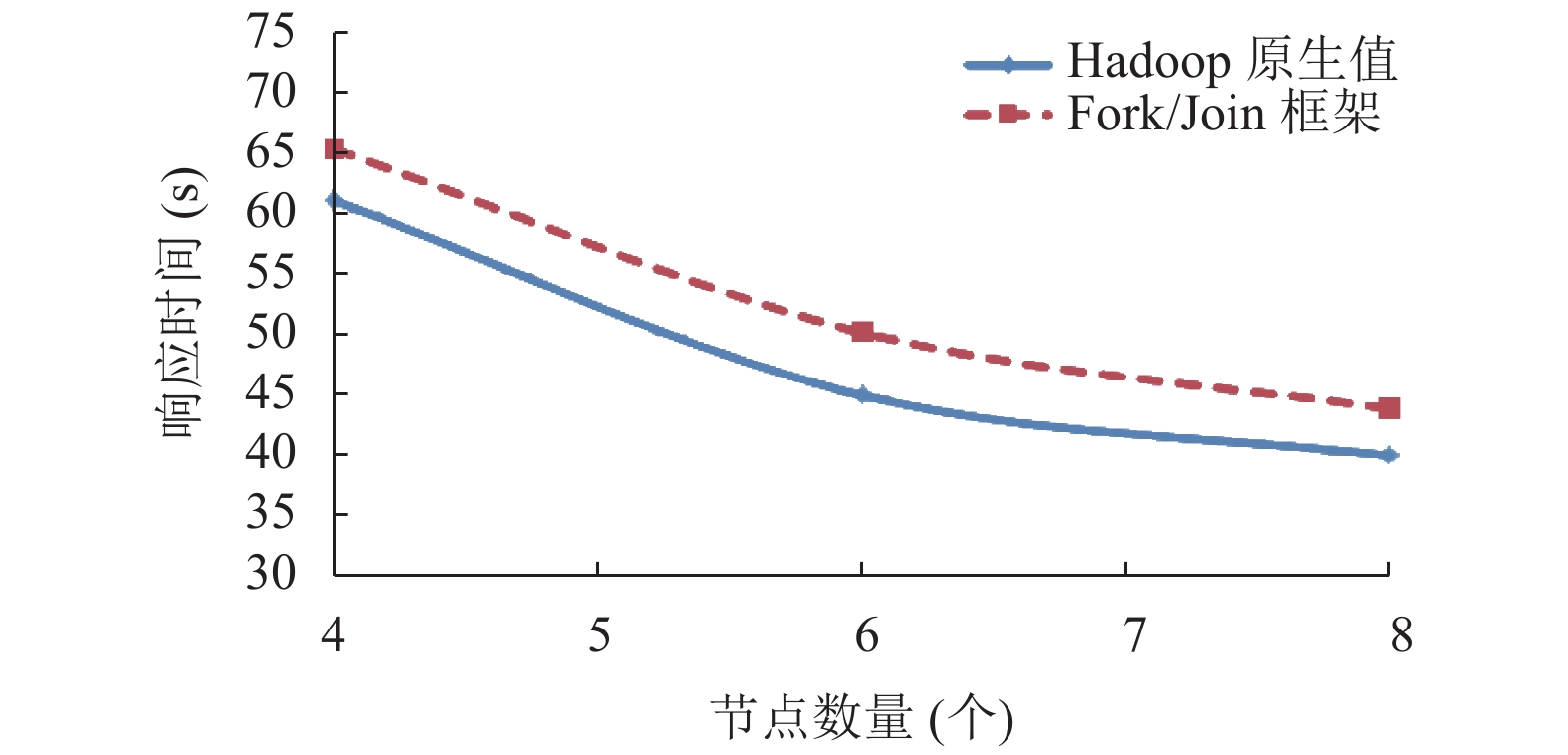
4.2 试验结果使用固定的输入数据, 在集群中使用不同数量的节点(4个, 6个, 8个), 并发地执行不同数量的作业(1个, 4个). 图中使用实线表示Hadoop1.x原生值, 使用虚线表示基于Fork/Join框架的计算值. 输入数据量为1 GB和5 GB的实验结果分别如图6–图9所示. 使用固定输入数据在集群中同时执行不同的作业数量(从1个到4个)的响应时间如图10所示.
|
图 6 作业数量1, 输入数据量1 GB |

|
图 7 作业数量4, 输入数据量1 GB |

|
图 8 作业数量1, 输入数据量5 GB |
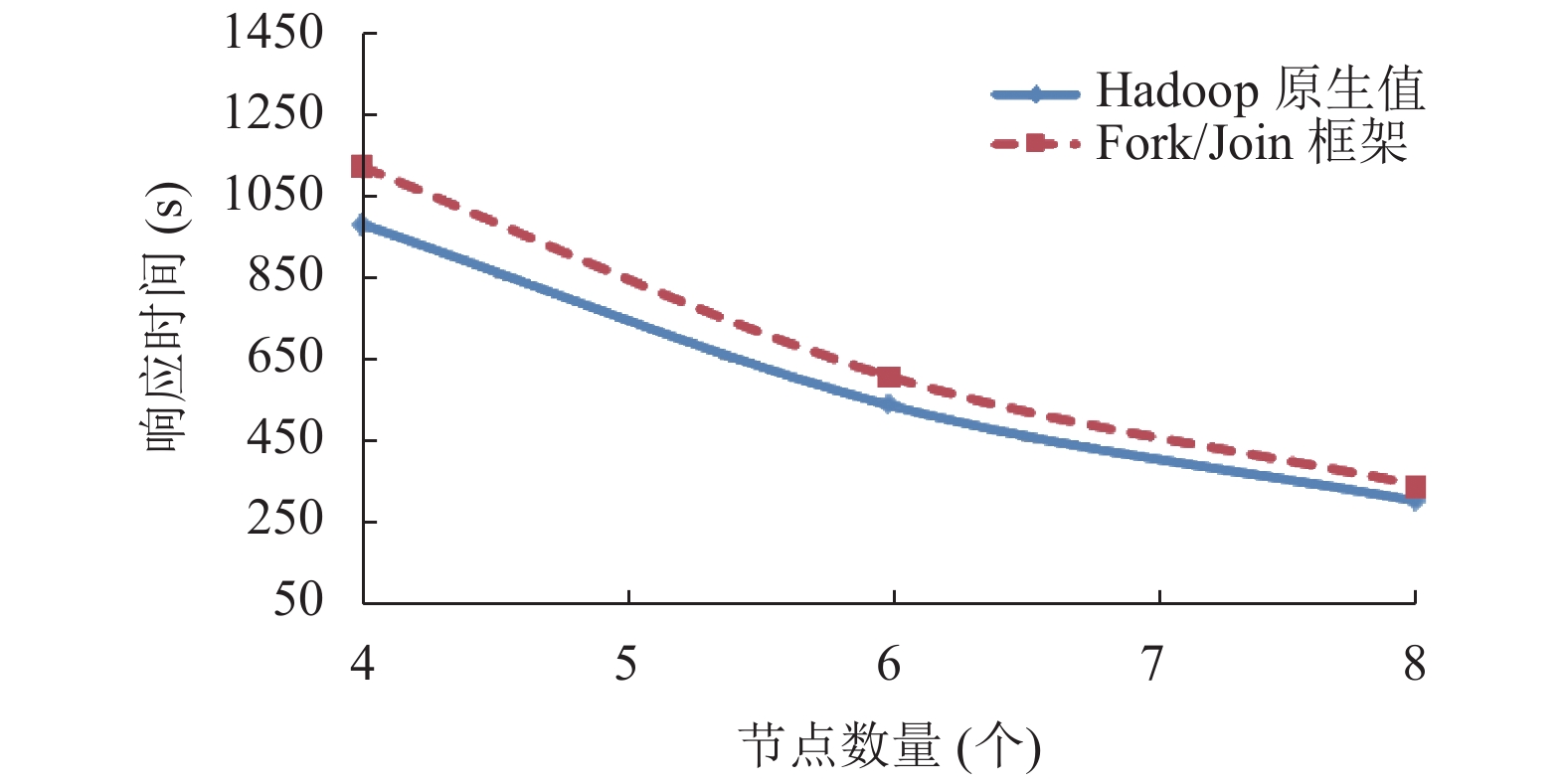
通过实验发现, 基于Fork/Join框架的算法的误差在11%到13.5%之间, 当输入数据量为5 GB的时候, 误差值达到最大13.5%. 假设算法的准确性取决于Map任务的数量而不是输入数据量. Map任务越多优先级树越复杂(深度越大), 所以出现误差的值就越大. 为了证明这个假设, 在实验中增加Map任务的数量而不增加输入数据量, 将Map任务的数据块从128 MB减小为64 MB. 实验结果如图11所示, 当输入数据量为5 GB, 作业数量为1个的时候, 误差值为17%, 是实验中得到的最大值. 当优先级树的最大深度减小时, 误差也会降低.
|
图 9 作业数量4, 输入数据量5 GB |

|
图 10 节点数量4, 输入数据量5 GB |

|
图 11 数据块64 MB, 作业数量1, 输入数据量5 GB |
基于Fork/Join框架的算法比Hadoop1.x原生方法提供了更加准确的结果, 可以进一步调整开销模型, 通过计算作业叠加因素的变化来提高准确性.
5 结论本文解决了为Hadoop2.x创建MapReduce性能评估模型的问题. 该模型考虑了由于共享资源争用而导致的排队延迟, 以及在同一作业中进行协作的各任务之间由于优先级约束而导致的同步延迟(Map阶段和Reduce阶段). 该模型的构建方法通过在Hadoop1.x性能评估模型的基础上扩展得到, 用优先级二进制树表示作业的执行流程, 用封闭式排队网络捕获物理资源上的争用. 通过对Hadoop2.x的资源管理与任务调度方法进行分析, 考虑到Hadoop2.x架构中资源分配改为动态方式, 作者创建了时间线构造算法, 并在此方法的基础上构建出优先级树.
在实验中从同时执行的不同数量作业的真实Hadoop设置值中获得测量值, 使用实验测量值对该模型进行验证: 使用标准数据块(128 MB)计算出作业响应时间的平均误差在11%和13.5%之间. 该模型可用于理论上估计作业响应时间, 所用成本要比实际中设置实验数据低得多. 该模型对于作业负载管理和资源分配规划中的决策也能够起到辅助作用.
| [1] |
李元亨, 邹学玉. Hadoop综述. 电脑知识与技术, 2018, 14(9): 8-9. |
| [2] |
司雅楠. Hadoop2.0平台概述. 科技与创新, 2019(5): 65-66. |
| [3] |
郭玉栋, 左金平. 基于Hadoop改进的云任务调度算法研究. 晋中学院学报, 2019, 36(3): 56-60. DOI:10.3969/j.issn.1673-1808.2019.03.013 |
| [4] |
马生俊, 陈旺虎, 郭宏乐, 等. Hadoop集群中影响应用性能的因素分析. 小型微型计算机系统, 2018, 39(4): 719-724. DOI:10.3969/j.issn.1000-1220.2018.04.018 |
| [5] |
朱洁, 顾烨君, 柳飞, 等. Hadoop负载树任务调度算法. 软件导刊, 2018, 17(12): 69-72, 76. |
| [6] |
李耘书, 滕飞, 李天瑞. 基于微操作的Hadoop参数自动调优方法. 计算机应用, 2019, 39(6): 1589-1594. DOI:10.11772/j.issn.1001-9081.2018122592 |
| [7] |
王凌晖, 解云月, 周美华. Hadoop分布式存储架构的性能分析. 现代电子技术, 2018, 41(18): 92-95. |
 2021, Vol. 30
2021, Vol. 30


