在机器学习中, 回归问题同分类问题一样一直是一个兼具魅力和挑战的热门研究领域. 回归建模过程是通过算法学习寻找已有数据之间的关联, 求得一个复杂函数, 然后给出预测结果, 常用的回归算法有多元线性回归^[1]、支持向量机^[2]、决策树^[3]、极限学习机^[4]、人工神经网络^[5]等. 决策树算法由于具有抽取规则简单、对数据缺失值不敏感、模型易于构建、速度快、效率高等特点, 深受相关学者专家重视. CART (Classification And Regression Tree)决策树广泛应用于分类和回归问题, 本文主要针对研究回归问题, 目前CART回归树在医学, 农业, 环境, 石油, 煤炭, 电力, 气象等诸多领域都得到了大量的研究和应用, 效果显著, 对专业研究、生产实践都起到帮助和指导作用. 比如Sut等^[6]将回归树应用于颅脑损伤死亡率的预测; Müller等^[7]将增强回归树用于比较阿尔巴尼亚和罗马尼亚的耕地放弃决定因素的研究; Park等^[8]使用回归树建立了预测水库系统中的叶绿素的应激响应模型来控制藻华; Larraondo等^[9]提出一种基于循环回归树的机场天气预报系统; 董红召等^[10]将回归树用于城市交通道路氮氧化物浓度的预测研究; 郑向群等^[11]提出一种空间数据挖掘算法, 使得空间关系变得简单, 以此提高了算法效率; 杜春蕾等^[12]提出一种改进的CART算法决策树模型, 用来处理煤层底板突水数据预测, 缩短了算法运行的时间, 也提高了准确率; 刘云翔等^[13]引入Fayyad边界判定定理, 使得挑选属性最优阈值的速度更快, 提高了运行效率; 毕云帆等^[14]将梯度提升机与决策树相结合得到梯度提升决策树, 提高了电力短期负荷预测精度; 李正方等^[15]调整决策树生成过程使其具有增量学习的能力, 提高了在气象信息系统中的实用性等等. 很多专家学者们深入研究决策树相关算法, 并对决策树算法做出很多的改进优化, 并凭借这些改进算法更好的适应解决了相应研究领域的问题, 也获得了良好的效果, 但决策树本身仍存在一些问题有待研究改进, 如叶节点的输出值计算方式为该节点处全部样本的平均值, 即模型训练好后的预测输出值为有限个定值, 这种预测输出值计算方法并不合理, 并没有实现真正意义上的回归预测, 导致回归预测的准确性大大降低, 降低了泛化的能力, 可能在一些特定数据集上表现良好, 但不适合广泛的应用于一般数据集. 因此, 为了提高准确性, 本文提出了该ELM-CART算法, 希望在回归树创建过程中, 通过在叶节点对样本子集分别采用ELM (Extreme Learning Machine)算法快速建模, 以此来构建合理的预测输出值, 提高预测准确性, 增强泛化能力, 实现真正意义上的回归预测.

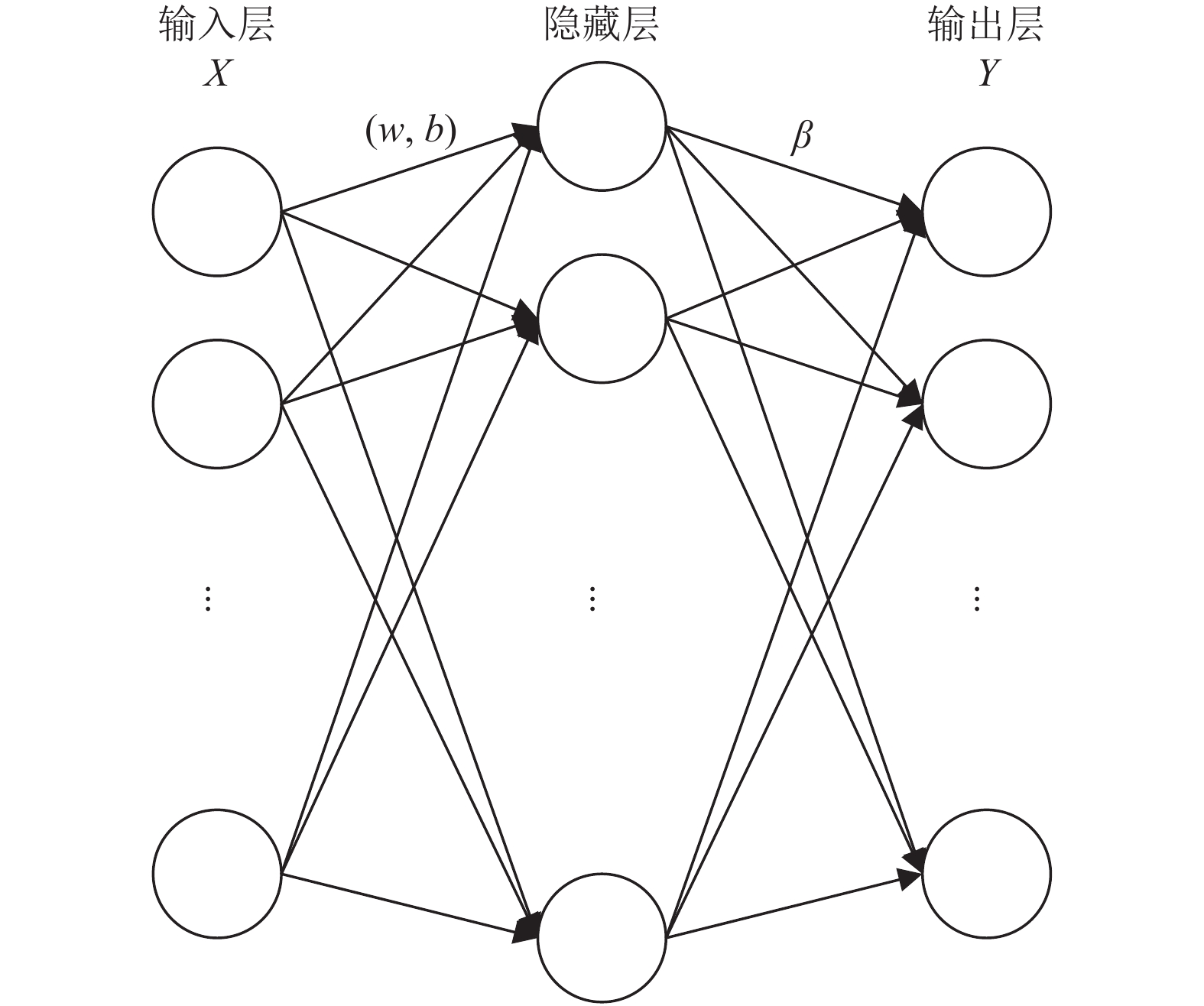
1 相关算法介绍 1.1 极限学习机算法

二十一世纪初, 黄广斌等提出极限学习机算法 ^[16]. 在此之前, 单隐层前馈神经网络(Single Hidden Layer Feedforward Neural Network, SLFN)是基于梯度的算法训练而成的, 而极限学习机并没有采用梯度算法, 而是随机生成输入层权重和隐藏层偏置. 然后通过已知数据的输入, 在使得损失函数最小的情况下, 得到输出层权重, 到此整个极限学习机就训练完成了, 通过已知的输入层权重, 隐藏层偏置以及输出层权重就可以直接计算测试数据的预测值了. 与其他算法比, ELM学习速度快、训练参数少、泛化能力强^[17]. 其网络结构如图1所示.

这里假设给定训练集 $\left\{ {{x_i},{t_i}|{x_i} \!\!\in \!\!{R^D},{t_i}\!\! \in \!\!{R^m},i \!\!=\!\! 1,2,\cdots,N} \right\}$ , 其中 ${x_i}$ 表示第 $i$ 个数据示例, ${t_i}$ 表示第i个数据示例对应的标记, 所有的训练数据组成一个集合, 假设该网络中有L个隐层节点, 即:

$\sum\limits_{i = 1}^L {{\beta _i}g({W_i} \cdot {X_i} + {b_i})} = {o_j},\;j = 1, \cdots ,N$

(1)

其中, 输出层权重为 ${\;\beta _i}$ , 激活函数为 $g(x)$ , 输入层权重为 ${W_i} = {[{w_{i,1}},{w_{i,2}}, \cdots ,{w_{i,n}}]^{\rm{T}}}$ , ${b_i}$ 为第i个隐层单元偏置. 算法学习的期望是最小化真实值与输出值的误差, 可以矩阵表示为:

$H\beta = T$

(2)

式(2)中, 输出层权重用 $\;\beta$ 表示, 而T表示期望的输出, 隐藏层节点的输出用H表示, 其具体形式可表示为:

$H({x_j}) = g({W_i} \cdot {x_j} + {b_i})$

(3)

网络中随机生成输入权重 ${W_i}$ 和隐层偏置 ${b_i}$ , 然后得到输出矩阵H, 这时, 极限学习机的训练过程就可以看做是线性问题的求解过程, 因此, 通过以下公式就可以求解出输出权重 $\;\beta $ , 可表示为:

$\beta = {H^ + }T$

(4)

其中, H⁺是矩阵H的Moore-Penrose广义逆, 且可证明求得的解 $\;\beta $ 的范数是最小并且唯一的.

1.2 CART决策树回归算法

在经典机器学习算法中, 决策树相关算法一直是研究热门, 因其独特的树形结构有利于快速处理数据, 表达数据之间的关联. 分类回归树算法简称CART算法 ^[18,19]. 最初是由Breiman^[20]于1984年提出的, 可生成分类树或回归树. 与ID3^[21]不能处理连续型数据相比, CART引入二元切分法即可处理连续型数据, 且适合于对多特征变量的复杂数据进行建模, 具有抽取规则简单、准确度高、可解释性强的优势, 但算法稳定性差, 容易过拟合.

假设X与Y分别为输入和输出变量, 且Y为连续变量, 给定训练数据集:

${{D}} = \{ ({x_1},{y_1}),({x_2},{y_2}), \cdots ,({x_N},{y_N})\} $

(5)

对于输入空间的划分,子空间及其输出值与叶节点一一对应. 这里通过依次遍历每个特征变量及其对应的每个特征值, 假设当前切分变量为第j个变量, 对应切分特征值为s, 即可划分并定义两个区域:

$\left\{ \begin{array}{l} {\alpha _1}(j,s) = \{ x|{x^{(j)}} \le {\rm{s}}\} \\ {\alpha _2}(j,s) = \{ x|{x^{(j)}} > {\rm{s}}\} \\ \end{array} \right.$

(6)

通过上述步骤, 输入空间将被不停的分割成L个子空间 ${\alpha _1}$ , ${\alpha _2}$ , …, ${\alpha _L}$ , 每个子空间 ${\alpha _l}$ 都包含部分的样本数据和输出值 ${\;\beta _l}$ , 这时模型的解可表示为:

$f(x) = \sum\limits_{l = 1}^L {{\beta _l}I(x \in {\alpha _l})} $

(7)

假设此时已经完成输入空间的划分, 这时的损失函数的误差大小可以采用平方误差 $\displaystyle\sum {{{\left( {{y_i} - f\left( {{x_i}} \right)} \right)}^2}} $ 来对比, 通过平方误差最小化的准则, 确定最优切分点和预测值. 又根据最小二乘的原理可知, 子空间 ${\alpha _l}$ 上的所有输出 ${y_i}$ 的均值即为 ${\;\beta _l}$ 的最优值 $\hat {{\;\beta _l}}$ , 即可表示为:

$\hat {{\beta _l}} = ave({y_i}|{x_i} \in {\alpha _l})$

(8)

划分输入空间的关键是如何选择最优的切分属性j和属性值s, 用公式表达为:

$\mathop {\min }\limits_{j,s} \left[ {\mathop {\min }\limits_{{\beta _1}} \sum\limits_{{x_i} \in {\alpha _1}(j,s)} {\mathop {({y_i} - {\beta _1})}\nolimits^2 } + \mathop {\min }\limits_{{\beta _2}} \sum\limits_{{x_i} \in {\alpha _2}(j,s)} {\mathop {({y_i} - {\beta _2})}\nolimits^2 } } \right]$

(9)

通过遍历全部的输入特征变量及其特征值, 就可以找到当前最优的切分点 $(j,s)$ , 然后根据切分点划分当前空间为两个子区域, 此时若这两个子区域无法再划分时, 即可得到相应的最优输出值, 表示为:

$\left\{ \begin{array}{l} {\hat \beta _1} = ave({y_i}|{x_i} \in {\alpha _1}(j,s))\\ {\hat \beta _2} = ave({y_i}|{x_i} \in {\alpha _2}(j,s)) \end{array} \right.$

(10)

根据以上步骤, 若该区域仍可继续划分,则对该区域重复上述步骤, 直到整个回归树完全不可划分停止.

2 ELM-CART回归算法

相比于线性回归, 树回归更适合处理复杂非线性的问题, 即便如此, 当输入数据特征维度较高, 特征之间关系相对更加复杂时, 构建全局模型往往导致准确性较低. 考虑到提高回归预测的准确性, 可以将输入数据集划分成若干个子集更易于建模.

经研究发现一般回归树在建立过程中, 就是将输入数据样本空间划分成若干个子样本空间, 每个子样本空间都有唯一确定的输出值, 这是因为在叶节点采用该节点处的样本平均值作为模型回归预测值, 也就是说回归树拟合出来的是一个分段零阶函数, 这些有限的离散定值极大程度上降低了决策树在回归问题上的预测准确率, 因此, 本文认为回归树叶节点处的样本子集还可以做进一步的处理, 这里可以对每一个子集分别进行建模, 充分利用叶节点处样本子集内部的特征关系, 理论上是可以达到提高整个回归预测准确率的效果. 结合ELM优点, 本文提出一种对CART回归树算法的改进算法——基于ELM的改进CART决策树回归算法(an improved regression algorithm for CART decision tree based on ELM, 简称ELM-CART算法).

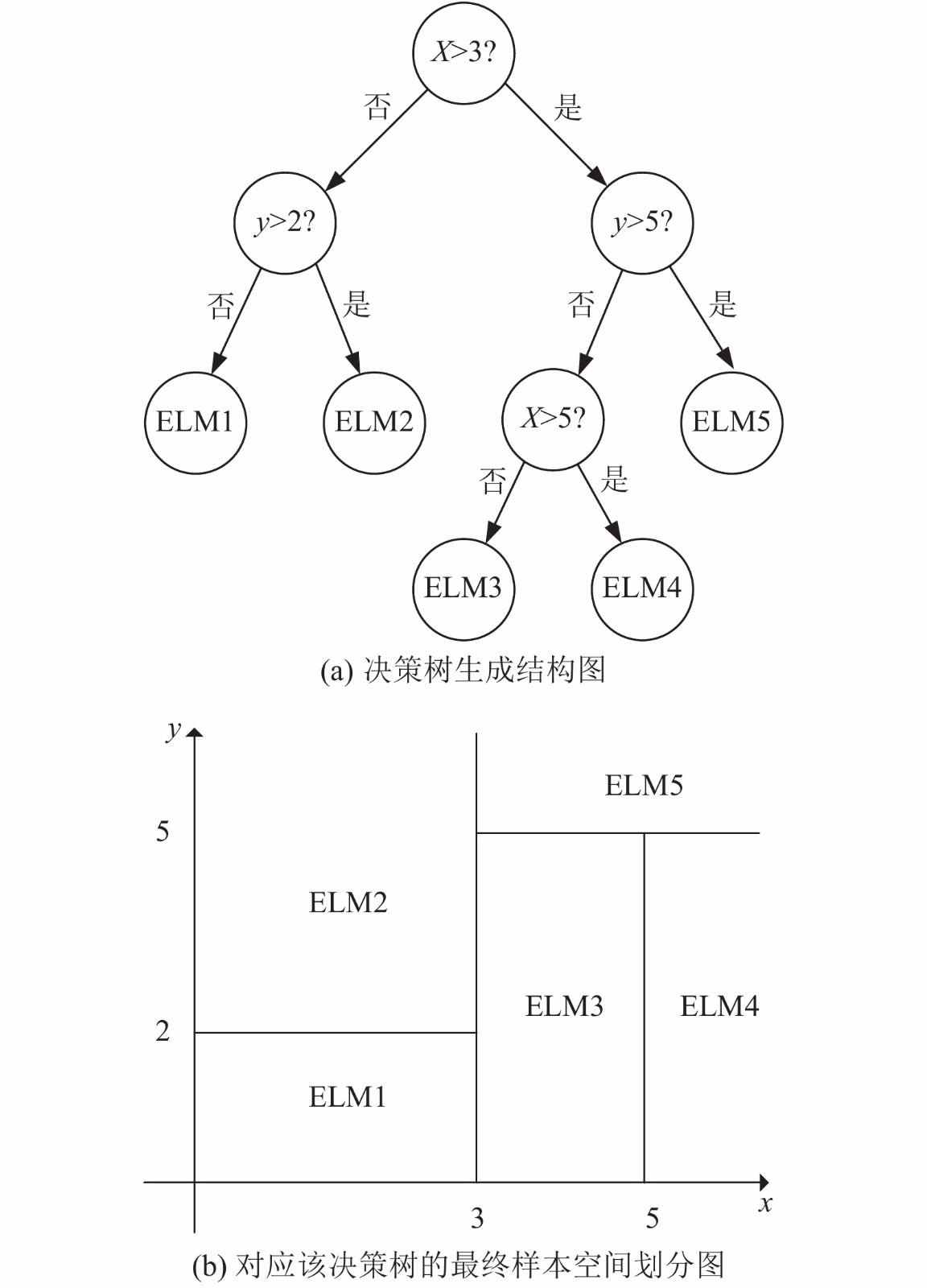
2.1 算法原理

本算法在回归树创建过程中, 采用二元切分法递归创建二叉树, 每一次将原输入空间划分成两个独立的子区域, 划分时希望划分的两个分支的误差越小越好, 这使得每次的划分都是独立且最优的, 越往树的底层深入, 节点覆盖的样本越少, 即随着树的生长, 估计越来越不可靠, 因此可以通过设置树停止生长的规则来提前结束树的生长, 以此避免过拟合, 达到最优树. 在决策树生成结束后, 在每一个叶节点处分别采用极限学习机对子集进行建模, 以此来达到提高回归预测的准确性, 如图2示例所示.

假设X与Y分别为输入和输出变量, 且Y为连续变量, 训练集为 ${{D = \{ (}}{{{x}}_1}{\rm{,}}{{{y}}_1}{\rm{),(}}{{{x}}_2}{\rm{,}}{{{y}}_2}{\rm{),}}\cdots{\rm{,(}}{{{x}}_N}{\rm{,}}{{{y}}_N}{\rm{)\} }}$ , 其中 ${x_i} = ({x_i}^{(1)},{x_i}^{(2)},\cdots,{x_i}^{(n)})$ 为输入特征数据, n表示为特征维数, $i = 1,2, \cdots ,N$ , N表示输入数据个数.

对输入样本空间的划分采用启发式方法, 每次划分都循环遍历当前空间中的全部特征变量及其对应的所有特征值, 再依据平方误差最小化准则唯一确定最优的切分特征和特征值组合. 假设确定当前训练集R的第j个特征变量 ${x^{\left( j \right)}}$ 及其取值s为切分点, 则有 ${R_1}\left( {j,s} \right) = \left\{ {x|{x^{\left( j \right)}} \le s} \right\}$ 和 ${R_2}\left( {j,s} \right) = \left\{ {x|{x^{\left( j \right)}} > s} \right\}$ 两个划分的定义区域, 因此, 是否划分以及划分的最优切分点选取可由式(11)和式(12)平方误差和比较得出:

$err = \sum\limits_{{x_i} \in R(j,s)} {\mathop {({y_i} - {c_i})}\nolimits^2 } $

(11)

$er{r_{1,2}} = \mathop {\min }\limits_{j,s} \left[ {\mathop {\min }\limits_{{c_1}} \sum\limits_{{x_i} \in {R_1}(j,s)} {\mathop {({y_i} - {c_{1i}})}\nolimits^2 } + \mathop {\min }\limits_{{c_2}} \sum\limits_{{x_i} \in {R_2}(j,s)} {\mathop {({y_i} - {c_{2i}})}\nolimits^2 } } \right]$

(12)

总之, 就是在小于 $err$ 的 $er{r_{1,2}}$ 中, 找出使得两个子区域平方误差和之和 $er{r_{1,2}}$ 最小的j和s, 其中, 这里c, ${c_1}$ 和 ${c_2}$ 的求解是通过ELM模型求得的估计值. 这里根据设置的隐含层节点数L, 随机初始化生成服从任意的连续概率分布的输入权重 ${w_i}$ 和隐含层阈值 ${b_i}$ , 就可以通过下式计算得到输出矩阵H.

${H_i}({x_j}) = g({w_i} \cdot {x_j} + {b_i})$

(13)

这里 ${x_i}$ 为输入向量, $g\left( x \right)$ 表示激活函数, 这里使用Sigmoid函数. 接下来计算此时的输出权重 $\;\hat \beta $ , 基于结构风险最小化的原则, 为了避免出现矩阵无法求逆以及防止模型的过拟合, 提高算法的泛化能力和鲁棒性, 引入L₂正则化项后, 此时输出权重 $\;\hat \beta $ 的计算公式为:

$\hat \beta \left( {{H^{\rm{T}}}H + \frac{1}{C}} \right){^{ - 1}}{H^{\rm{T}}}T$

(14)

其中,C为正则化系数. 由此根据式(13), 式(14)即可分别求得当前训练集R, ${R_1}$ 和 ${R_2}$ 的输出矩阵H, ${H_1}$ , ${H_2}$ 和输出权重 $\;\hat \beta $ , ${\;{\hat \beta _1}}$ , ${\;{\hat \beta _2}}$ , 于是通过下式即可分别求得式(11), 式(12)中的 $c$ , ${c_1}$ 和 ${c_2}$ .

$\left\{ \begin{array}{l} c{\rm{ = }}H \hat \beta \\ {c_1}{\rm{ = }}{H_1}{{\hat \beta _1}} \\ {c_2}{\rm{ = }}{H_2}{{\hat \beta _2}} \\ \end{array} \right.$

(15)

于是, 根据以上步骤, 若该区域仍可继续划分,则对该区域重复上述步骤, 直到整个树完全不可划分停止.

对数据集进行训练过程中, 控制树的划分次数, 既可以减小时间开销; 又可以防止过度划分导致模型出现过拟合. 因此, 本算法设置3个超参数作为算法结束条件, 满足任意一个即训练结束: (1)树的深度达到给定深度; (2)误差小于容许的误差下降值; (3)叶节点处的子区域数据量小于设定的数量.

3 实验分析 3.1 数据选取及处理

本文测试数据来自加州大学欧文分校的UCI(University of California Irvine)数据库, 这里面的数据集主要分为分类和回归两大类, 在很多机器学习算法的相关论文中都可以看到这些数据集的应用. 本次实验涉及的数据集分别有波士顿房价数据集, 鱼类毒性数据集, 翼型自噪声数据集, 联合循环电厂数据集, 混凝土抗压强度数据集, 水生毒性数据集以及加利福尼亚房价数据集等, 详细介绍如表1所示.

首先下载这些数据集文件, 然后读取不同类型文件并对格式进行处理统一, 再对数据归一化处理, 有利于提高模型的训练速度和准确性, 最后将数据集分为训练集和测试集, 为进一步的实验做好数据准备.

3.2 评价指标

本文采用均方误差(Mean Squared Error, MSE), 平均绝对误差(Mean Absolute Error, MAE)以及R²值(R Squared) 3种评价指标.

MSE值越接近零, 表明模型越好, 其公式如下:

$MSE=\frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{y_i} - {{\hat y_i}} } \right)}^2}} {\rm{ }} $

(16)

MAE值越小, 模型也就越好, 其公式如下:

$MAE=\frac{1}{m}\sum\limits_{i = 1}^m {|{y_i} - {{\hat y_i}} |} $

(17)

R²值不同于前两者, 它的范围为0–1之间, 并且随着R²值增大, 训练模型的准确率也越来越高, 当R²等于0时意味着不必进行预测, 常数模型直接取值的情况; 相反, 当R²等于1时, 意味着所有预测值跟真实值是完全相等的, 也就是说模型是不犯错的, 这也是回归分析中追求的理想结果, 其公式如下:

${R^2} = 1 - \frac{{\displaystyle\sum\limits_i {{{\left( { {{\hat y_i}} - {y_i}} \right)}^2}} }}{{\displaystyle\sum\limits_i {{{\left( {\bar y - {y_i}} \right)}^2}} }}$

(18)

式中, m代表样本总数, $\bar y$ 为真实平均值, ${y_i}$ 和 ${{\hat y_i}}$ 分别为第i个样本的真实值和预测值.

3.3 实验结果分析

本文基于以上标准数据集, 将ELM-CART回归算法与回归树, ELM, SVR, 人工神经网络算法等进行对比分析, 其中回归树的容许误差下降值默认设为1, 切分的最小样本数取值在10以内; ELM的L₂正则化参数C取值为100000, 隐层节点数设置有20, 50, 1000及1200; SVR采用的是使用最广泛的径向基核函数(RBF); 人工神经网络采用的是两层及三层的神经网络; ELM-CART算法可以设置树的深度, 一般默认为2, 通过增加深度可以起到进一步划分数据集的效果, 原CART中保留的切分最小样本数基本同树的深度效果一样, 隐层节点数大于20. 通过MSE, MAE以及R²值3种评价指标得到以下结果, 如表2所示.

通过表2对比可知, 在这些标准数据集上, 本改进算法总体上在MSE, MAE, R²值的对比中都明显优于CART回归树算法和ELM算法, 同时也总体略优于SVR和人工神经网络. 由于MSE评价指标采用平方计算使得对异常样本更加敏感, 通过对比boston_housing、airfoil_self_noise、CombinedCyclePowerPlant、ConcreteCompressiveStrength等数据集上的MSE值, 不难发现改进算法的MSE值相对明显较小, 这是因为在改进算法中引入了L₂正则化项, 添加了惩罚项使得改进算法在MSE评价指标下对比其他算法得到明显的下降, 使得模型更加适应异常样本存在的情形. 其次, 对比MAE值可以看出, 改进算法在这些数据集上的表现总体是优于所对比算法的. 接着从R²值对比来看, 很明显改进算法的结果要优于其他算法, 特别是明显优于CART回归树算法和ELM算法, 甚至在airfoil_self_noise等数据集上有显著提高, 表明模型的准确率也更高. 利用CART算法对数据集的划分原理使得相关关系更紧密的样本数据划分到一起, 从而将全局模型的构建转化为多个局部模型的构建, 使得对比CART回归树和ELM明显提高了预测的准确性. 因此, 改进算法是将两个算法的优势结合在一起, 整体而言, 本文提出的改进算法达到了预期效果.

4 结论与展望

本文提出了基于ELM的改进CART决策树回归算法, 将复杂的全局模型分解为多个相对容易的局部模型, 从而降低回归分析的难度, 提高模型准确性, 并结合ELM具有的优点, 将CART回归树与ELM算法融合, 弥补了CART回归树算法本身的缺点与不足, 达到提高回归预测的准确率, 并通过上述实验结果对比表现出了改进算法的优化效果. 在接下来的工作中, 将会在更多数据集上测试算法的准确性, 同时将会继续研究相关算法, 以期进一步提高回归预测精度及稳定性.