随着计算技术的发展, 数字图像处理技术的使用越来越普遍, 在医学工程、计算机工程、宇航制导、航空航天等研究领域都有大量数字图像处理技术的使用[1]. 在数字图像处理中, 要进行图像的汇聚、模糊处理、边缘增强和边缘检测等典型算法中都要使用卷积作为核心运算单元. 随着近年来深度学习技术在图像识别领域的极大成功, 卷积神经网络(CNN)受到越来越多的关注. 而要提高CNN的计算性能, 就需要高效的卷积实现. 基于现场可编程门阵列(FPGA)实现高速图像处理系统一直是一个非常活跃的研究领域, 这主要得益于FPGA的位级并行计算能力、像素级处理以及邻域级与任务级的处理能力, 可使得计算和速度达到更好的性能. 另外, FPGA是可重配置的, 从而能够更好的满足神经网络的灵活性需求. 正是FPGA这种兼具灵活性与并行处理的能力, 使其成为开发神经网络硬件加速计算领域的首选平台[2].
针对图像卷积实现的问题, 有不少学者进行了研究, 大部分工作集中在高性能、低资源以及FPGA面积使用效率上. 正如文献[3]所指出的, 块随机存取存储器(BRAM)是经常使用的一种解决方案, 但这种方案是以较高的能耗为代价的. 为了降低能耗, 在结构设计上, 可以通过图像部分性存储或完全存储来减少BRAM的使用. 对于完全性图像存储, 主要通过应用并行化提高处理能力, 并通过资源重用降低复杂性. 对于部分存储架构, 则是将图像分割成与使用的卷积器一样多. 这些方案的缺点是模块化设计不够, 使得难以简单通过增加并行度来提高工作效率[4–6].
为此, 本文提出了一种基于动态重用BRAM的图像卷积模块化实现架构, 并给出了并行结构实现中的复杂度. 实验表明, 当并行度提高时, BRAM的复杂度只是线性增加, 这无疑会极大降低系统功耗和复杂度.
本文安排如下: 第2部分简要介绍图像卷积算法及设计流程. 第3部分介绍了模块化设计架构及各模块的组成. 在第4部分, 给出了硬件实现和实验结果. 最后, 给出本文结论.
1 图像卷积算法得益于卷积固有的局部提取和二维特性, 在图像处理算法中, 图像卷积运算是经常使用的. 由文献[3]知, 图像卷积的定义为:
| ${I'(x,y) = \sum\limits_{i = 0}^{m - 1} {\sum\limits_{j = 0}^{n - 1} {w(i,j)I(x - i,y - j)} } } $ | (1) |
其中, I(x, y)是大小为(m×n)的图像在(x, y)处的像素值, w(i, j)大小为(k×k)的卷积核, 由一组系数构成, 而
由于图像卷积算法的并行性非常适于FPGA实现, 从而提高计算性能, 所以本文将重点研究如何更有效进行二维卷积设计, 以减少FPGA资源的使用.
为了便于硬件实现, 这里主要采用图像的灰度值. 考虑到每个通道可以视为独立的灰度图像, 所以本文方法易于推广到具有多个通道的图像上.
对于图像像素I(x, y)的灰度值动态范围一般在[0, 255], 卷积核w(x, y)可以为负或正. 这里把像素灰度值做归一化处理, 也就是转换像素值为T[I(x, y)] =
| $I'(x,y) = {T^{ - 1}}\left[ {\sum\limits_{i = 0}^{m - 1} {\sum\limits_{j = 0}^{n - 1} {w'(i,j){I^{\rm{T}}}(x - i,y - j)} } } \right]$ | (2) |
其中, T−1(.)表示归一化处理的逆变换, 其范围为[0, 255]. 图1给出了整个数据映射过程, 先对输入图像进行归一化, 然后将其与内核进行卷积, 最后将计算结果进行逆变换以重新映射到标准灰度值.

|
图 1 图像处理映射关系图 Fig. 1 Map relationship of image processing |
对于硬件运算, 有浮点表示和定点表示[3]. 浮点表示以尾数和指数形式存储数字, 支持浮点格式的硬件在每次执行计算后会自动缩减尾数并更新指数, 以使结果与设定的位数相对应, 这些操作使支持浮点的硬件在面积和功耗方面牺牲较多. 一种替代方法就是定点表示. 定点表示主要存储和处理具有固定位的数据. 这意味着在计算之后, 不遵循小数点的位置, 小数点, 无论是否冗余, 对于每个变量都是固定的, 并且是预定义的. 这种设置在资源利用方面具有优势, 但如果计算结果超出范围, 发生溢出, 需要根据系统选择适当的表示形式.
为了以最小位数表示用于图像像素和内核值, 需要研究具有可接受的信息损失下的最小分辨率位数. 如前所述, 像素的值在0到255的范围内, 通过归一化, 限定为0到1的范围. 卷积核既可以是正数, 也可以是负数, 使用极大范数化使卷积核限制在−1到1的范围. 为了以8位表示上述值范围, 这里采用有符号定点表示S(8, 7). 假定图像以K3×3进行卷积会产生20位输出, 对于每个乘积结果乘以S(16, 14), 9个元素的总和为S(20, 14), 经过处理后, 将结果取正并截断, 去掉小数部分, 用S(13, 8) 表示.
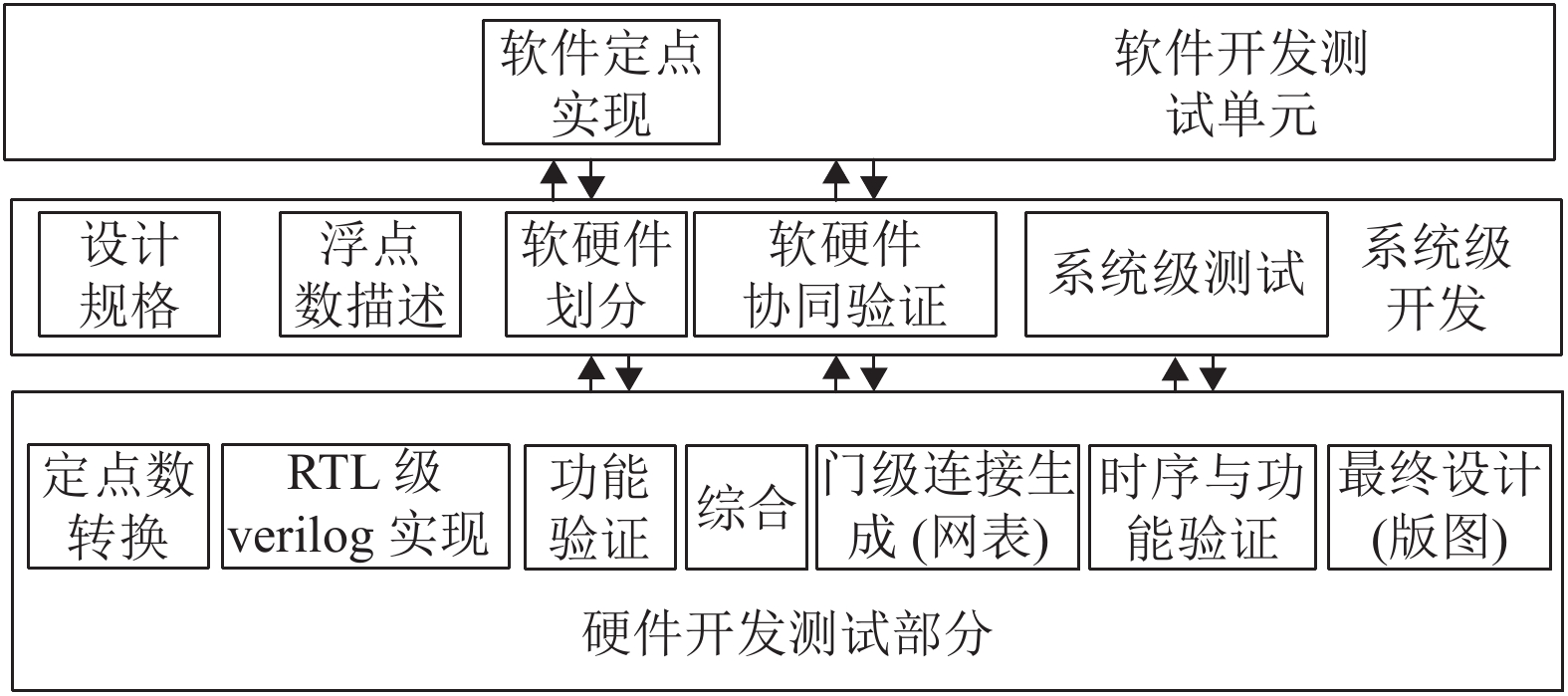
2 通用卷积平台设计架构 2.1 设计流程为了便于系统化和模块设计, 采取系统级软硬件协同设计方法, 整个设计流程图如图2所示. 首先, 基于设计规范, 进行软硬件划分; 在软件开发部分, 先通过上位机(采用Python语言)进行浮点计算的模拟, 然后, 在软件层面分析定点运算实现系统的结果, 验证所描述的硬件模拟器产生的位是否与浮点运算模拟器的位相匹配, 然后在FPGA中进行硬件设计. 在FPGA硬件设计中, 通过软硬件协同验证, 再次检查硬件验证的结果与模拟结果是否相同, 不同的话再进行定点位数的调整, 直到满足设计要求, 最后完成设计.
将整个设计流程分成以下几个阶段:
(1)预处理阶段: 通过上位机使用Python脚本利用第2节中提到的转换来获取图像. 上位机脚本程序可将映射图分成几批进行处理, 然后分批通过端口(UART)将其发送到下位机FPGA. 单个批次的连续像素大小由使用的MAC单元数量决定.
(2)处理阶段: 将批处理图像与卷积核进行卷积操作. 所述卷积核是可配置的, 用户可以通过GPIO加载相同的系数. 卷积操作完成后, 数据发送到FPGA中的微处理器, 并给出恢复批处理的顺序, 以便将其返回到上位机.
(3)后处理阶段: 在后处理中, 上位机使用Python脚本组合上传来的一个或多个批次图像像素, 并通过逆变换恢复为标准灰度值.
2.2 系统状态及流程图整个系统设计分成8个处理过程, 如图3所示. 启动后, 系统必须初始化, 通过接收初始化信号以使自身进入该状态, 等待配置. 接收到相应的指令后, 系统将进入卷积核系数装载状态, 即将卷积核系数加载到系统中. 紧接着进行待分批处理像素大小设置, 即图像的大小, 这决定了最后一个数据在内存中的位置. 状态的转换通过指令码的方式进行控制, 未收到指令码时, 系统保持状态不变. 批次存储后, 将进入卷积运算状态, 在此状态下完成批次卷积处理. 一个批次的图像处理完成后, 将发出通知, 并将批处理完的结果返回到上位机.
|
图 2 系统设计架构图 Fig. 2 Schematic of the design flow followed |

|
图 3 系统处理流程图 Fig. 3 Flow chart of system processing |
2.3 卷积模块结构设计
为了实现内存的动态复用, 即在每次批处理中重复使用内存加载的数据, 整个卷积实现系统采用图4所示的模块化设计. 主要包括接口控制单元: 负责卷积处理模块与嵌入式内核MCU之间的通信; 地址管理器(AMU): 用于生成待读取或写入数据的存储地址; 数据存储管理单元(DMU): 用于管理待写入或读取数据的存储空间; 乘累加器(MAC)单元: 执行卷积核系数和图像像素之间乘积累加和操作; 存储单元, 由FPGA的BRAM组成的一组存储单元, 大小取决于实例化的MAC数量, 即系统所需的卷积并行处理要求.
接下来, 具体阐述各个功能模块的具体实现方法.
2.3.1 存储单元为了批量存储, 采用BRAM列排的形式, 每一列对应于一个批次中的一栏. 批处理的大小由图像的高度和实例化内存数确定. 因此, 图像的最大高度(以像素为单位)必须小于或等于实例化内存的地址数. 在批处理期间, 每个像素只能读取一次, 从而可以更有效地使用内存. 已读取的批处理像素将被处理后的像素覆盖, 这样可以减少所需的内存量. 对于存储单元有两个数据端口, 一个用于输入数据, 一个用于输出数据, 还有一个读写控制信号.

|
图 4 卷积部分实现结构 Fig. 4 : General system architecture of Convolution module |
2.3.2 接口控制单元
接口控制单元模块负责模块与FPGA中的处理器之间的接口. 为此, 它具有两个32位端口, 分别连接到处理器的内部和外部的GPIO. 该单元主要通过接收指令完成以下控制功能: 加载卷积核, 用于加载卷积核系数, 每个系数设为8位; 配置图像尺寸, 必须与图像的高度(以像素为单位)一起使用, 使用10位, 因此最大尺寸为1024 px; 图像批处理加载, 一个批次的像素加载; 批处理完成, 表示正在加载的像素是批处理中的最后一个像素, 一旦收到此指令, 模块将进入运行状态, 在该状态下执行处理; 恢复数据, 要求模块提供下一个已处理的像素.
2.3.3 地址管理单元(AMU)AMU负责生成DMU占用的内存地址. 在图像加载状态期间, AGU负责生成写入此数据的地址, 为此, 它具有一个计数器, 该计数器随控制单元输入递增. AMU通过比较图像的高度, 向DMU发送指示信号, 表明接下来接收到的像素属于批次的新列. 在运行阶段, AMU必须产生两个不同的地址, 一个指向DMU传送到MAC单元的数据地址, 另一个指向DMU存储MAC处理后数据的地址. 两个地址每个时钟周期增加一次, 因为MAC生成每个周期处理的数据. 读地址和写地址之间的差等于从将第一个像素传送到MAC单元到准备好存储第一个已处理像素为止的等待时间.
2.3.4 乘法累加器单元(MAC)MAC是并行实例化的单元, 它们负责进行乘加计算以执行卷积. 对于卷积核(3 × 3)的卷积运算需要9条记录存储系数以及9条记录存储当前正在处理的批次像素值. MAC具有单个数据输入端口, 其中输入了3个系数(对应于一行)的卷积核或批处理部分(如来自控制单元的信号所示), 此外还有另一个控制信号, 用于指示应修改记录还是保持.
对于大小为(k×k)的内核, 加载每列的k个像素, 在其中保留(k×k)个像素, 然后, 将像素乘以核系数, 将每个项相加. 对于最终求和结果, 送出前, 会做截断处理. 处理完像素后, 将存储批次像素的记录进行移位, 即新的一行, 它等效于FIFO 结构. 该操作的硬件实现如图5所示.

|
图 5 基于MAC的卷积硬件实现结构图 Fig. 5 Hardware implementation of the Convolution module based on MAC units |
2.3.5 数据存储管理单元(DMU)
为了有效利用存储器, 必须考虑并行度. DMU的作用就在于建立存储器和其余单元之间的接口, 从而独立于并行处理需求而降低其复杂性. 对于k×k的卷积核, 需要使用k列作为输入以在MAC中生成处理后的列. 因此, 对于两个MAC需要2k列. 对于卷积运算, 要得到连续的列, 必须将输入列移位一次. 那么对于MAC输入的相邻列就有可能存在重复, 所以可通过共享来降低开销.
这样的好处是, 与每个MAC单元都使用独立的存储器列相比, 在不同的MAC之间共享信息可以极大节省所需的BRAM, 而循环移位可以节省传输的信息量.
为了实现以上功能, 该模块在内部由两部分组成: 一个数据多路复用器模块, 用于传递存储器和MAC的信息; 一个基于有限状态机(FSM)的控制部分, 用于处理存储器的控制信号(写使能)和数据多路复用器的控制信号.
3 FPGA实现与结果分析 3.1 实验环境为了在FPGA中实现该设计, 本文选择使用了Vivado环境. 预处理(浮点模拟和图像归一化)和后处理(图像标准灰度值转换)均在上位机实现. 卷积核系数和相应的图像批处理都通过串口加载到FPGA 上. 在FPGA 的运算使用定点表示, 对输入和输出图像(处理后的图像)的分辨率设定为8位. 综合后的系统级模块图如图6所示.
3.2 实验结果通过上位机利用Python脚本构建不同的卷积核, 使用的卷积核包括: [0, 0, 0; 0, 1, 0; 0, 0, 0], [0, −1, 0; −1, 5, −1; 0, −1, 0]和[−2, −1, 0; −1, 0, 1; 0, 1, 2], 并在上位机对图像进行卷积处理. 然后, 采用相同的卷积核使用FPGA对图像进行卷积处理. 图7给出了上位机模拟结果和FPGA实现结果的比较.

|
图 6 系统功能单元图 Fig. 6 Each unit of the whole System |

|
图 7 上位机模拟效果与FPGA实现效果比较图 Fig. 7 Comparison of results: left, processed on PC, right, the same image processed with FPGA |
3.3 资源使用情况分析
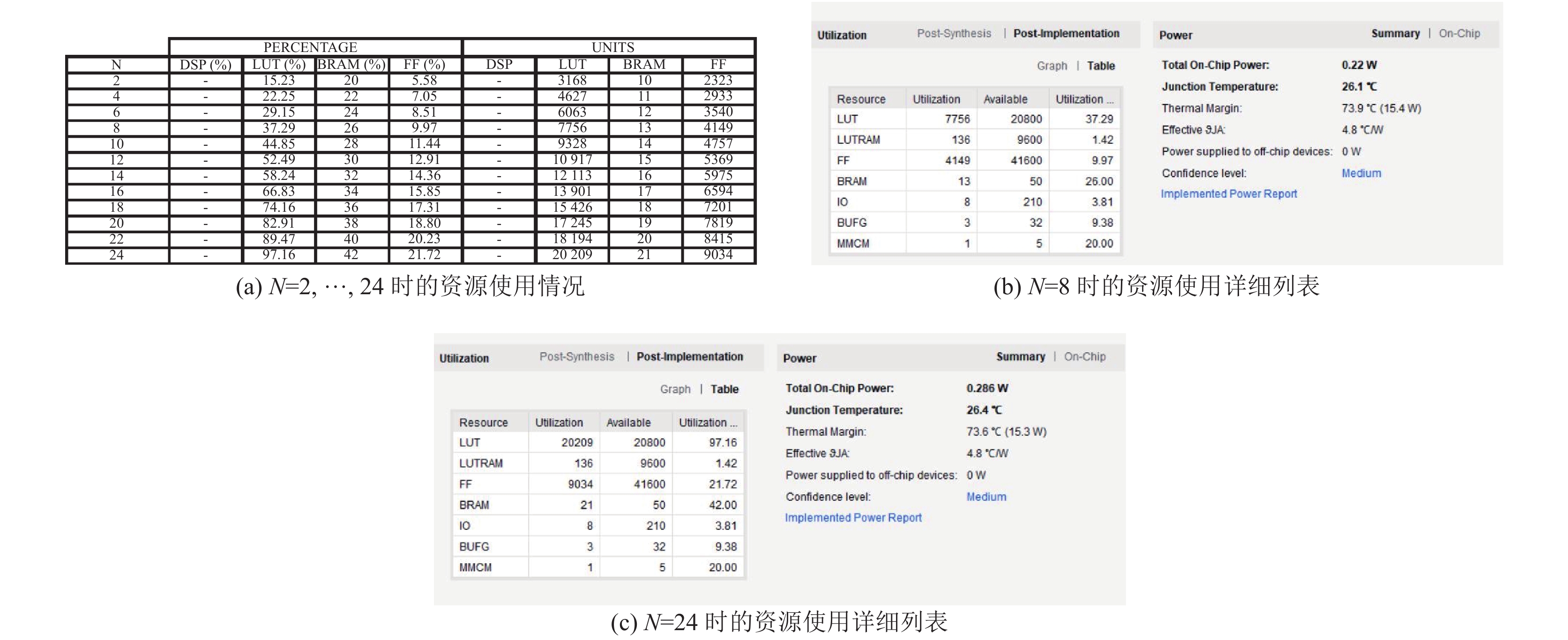
该设计针对不同程度的并行性需求进行了综合. 图8(a)分别给出了2个实例并行化至24个实例并行化的资源使用情况, 根据系统中的并行度, 可以看到复杂度呈线性增加. 图8(b)、图8(c)分别给出了8个实例并行化和24个实例并行化的资源使用详细分布. 图9给出了存储开销使用情况, 传统的图像卷积实现, BRAM基本是随着卷积单元数以1:1的比例增长, 本文的方法可以使得存储开销显著的下降.
|
图 8 资源占有情况分析 Fig. 8 Resource utilization analysis |

|
图 9 资源占有情况分析 Fig. 9 Memory utilization analysis |
4 结论
本文主要研究了如何在FPGA中模块化实现图像卷积运算. 在具体实现上, 主要采用了图像按列批次处理, 分批加载到FPGA上, 然后进行卷积运算, 在设计中利用临近批次数据重复性这一特征, 运用内存共享机制, 有效降低了BRAM的使用, 实验表明并行度的提高仅线性增加BRAM; 整个系统设计基于装载、处理、输出的流程机制, 可实现(k×k)卷积核的重配置, 具有较好的扩展性.
| [1] |
Aguilar-González A, Arias-Estrada M, Pérez-Patricio M, et al. An FPGA 2D-convolution unit based on the CAPH language. Journal of Real-time Image Processing, 2019, 16(2): 305-319. DOI:10.1007/s11554-015-0535-1 |
| [2] |
Abdelouahab K, Pelcat M, Sérot J, et al. Tactics to directly map CNN graphs on embedded FPGAs. IEEE Embedded Systems Letters, 2017, 9(4): 113-116. DOI:10.1109/LES.2017.2743247 |
| [3] |
Sriram VB, Sawant R, Kamath K, et al. Implementation of 2D convolution algorithm on FPGA for image processing application. International Journal of Electrical, Electronics and Data Communication, 2015, 3(12): 22-25. |
| [4] |
卢冶, 陈瑶, 李涛, 等. 面向边缘计算的嵌入式FPGA卷积神经网络构建方法. 计算机研究与发展, 2018, 55(3): 551-562. DOI:10.7544/issn1000-1239.2018.20170715 |
| [5] |
曾成龙, 刘强. 面向嵌入式FPGA的高性能卷积神经网络加速器设计. 计算机辅助设计与图形学学报, 2019, 30(9): 1645-1652. |
| [6] |
李小燕, 张欣, 闫小兵, 等. 基于FPGA的卷积神经网络加速系统. 河北大学学报(自然科学版), 2019, 39(1): 99-105. |
 2021, Vol. 30
2021, Vol. 30


