图像压缩是计算机学科学术界和工程界关注的热门研究领域之一[1,2]. 目前已有很多成熟的压缩算法, 也产生了各种图像压缩格式, 如JPG、GIF等[3]. 还有一些通用的文件压缩算法, 进而产生了各种文件压缩格式, 如ZIP、RAR等[4]. 奇异值分解方法是线性代数数学学科中一种数据压缩方法, 可以将大规模的矩阵在分解为矩阵的乘法表示后, 用一定比例的特征数据矩阵来表示原来的大规模矩阵, 从而达到压缩的目的. 奇异值分解方法可以运用到图像压缩领域, 并起到良好的压缩效果.
已有一些学者、工程技术人员将奇异值分解方法运用到特定的图像压缩应用上, 如视频监控图像、遥感图像等[5,6]. 还有的研究人员结合奇异值分解方法和其它的算法来提升图像的压缩比[7], 绝大多数研究工作采用的是Matlab开发工具[8,9]. 考虑到图像压缩算法多已成熟, 本文并不打算提出新的算法, 而是深入研究基于奇异值分解的技术原理, 提出2种运用奇异值分解作图像压缩的方法, 用Python编程实现并展开实验, 再对JPG、PNG这2种通用的图像格式作出压缩效果的示例和对比分析.
1 奇异值分解的原理奇异值分解可以针对任意形态的矩阵作特征值分解. 现实应用场景中的数据确实不太可能都是方阵, 而多是行数、列数不等的数据矩阵, 因此, 奇异值分解具有广泛的应用价值[10].
| $A_{m \times n} = U_{m \times m}D_{ m \times n}V_{n \times n}^{ - 1} = U_{m \times m}D_{m \times n}V_{n \times n}^{\rm{T}}$ | (1) |
式(1)中的
根据式(1), 如果将r个特征值从大到小排序, 并调动对应的
具体压缩方法是取前k个特征值, 及矩阵
| $A \approx \sigma_1u_1V_1^{\rm{T}} + \sigma_2u_2V_2^{\rm{T}} + \cdots + \sigma_ku_kV_k^{\rm{T}}$ | (2) |

|
图 1 奇异值分解的图示 |
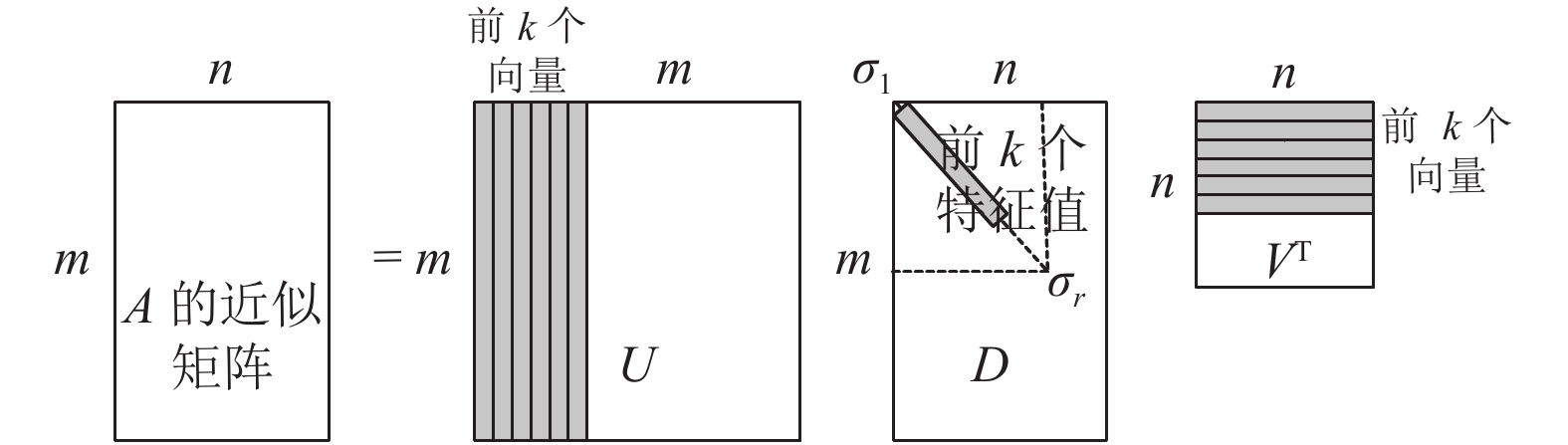
|
图 2 数据压缩的思想图示 |
这种数据压缩的思想体现的就是用数据的主要成份来代表整体数据, 从而实现只要存储较少的数据, 可见这其实是一种有损数据压缩, 因此需要将数据的压缩控制在可以接受的范围[15].
2.2 压缩比的计算经过如图2所示的变换后, 数据矩阵A的近似矩阵的行数和列数并没有变, 那又怎么是节约空间了呢?
这是因为奇异值分解后, 不必再存储数据矩阵A, 而是存储矩阵
以一个1000×2000的数据矩阵为例, 则要存储2000000个数据, 假定每个数据占用的存储空间数量相同. 假定运用奇异值分解共需使用50个特征值来作数据压缩, 存储矩阵
衡量这种节约的程度可用压缩比来表示, 按式(3)所示的公式计算:
| $ P=\frac{{S}_{\text{原}}}{{S}_{\text{压}}}$ | (3) |
式(3)中, P表示压缩比,
| $P = \frac{{2\;000\;000}}{{150\;050}} \approx 13.33$ |
k取值应为多少合适呢?那得看对数据压缩的目标需求了, k越大, 数据就压缩得越少, 需要的存储空间也越多, 需要找到一个合适的平衡点. 有2种方法:
(1)按特征值个数占比阈值取特征值个数. 设定一个比例阈值f, 如果k与特征值总个数之比的值超过阈值f, 则取前k个特征值.
(2)按特征值之和占比阈值取特征值个数. 设定一个比例阈值f, 如果前k个特征值之和与所有特征值之和的比的值超过阈值f, 则取前k个特征值.
2.4 图像压缩的原理以常用的PNG和JPG格式的图像为例, 读取它们的图像数据可得到一个3维的数据矩阵. 第1维表示的横向的像素, 第2维表示纵向的像素, 第3维表示图像的通道, 用0~255范围的数据表示数据值.
PNG和JPG两种格式不同的是, PNG格式图像的第3维有4个通道, 分别表示R (Red, 红色)、G (Green, 绿色)、B (Blue, 蓝色)、A (Alpha, 透明度); 而JPG格式图像只有R、G、B这3个通道, 没有A这个通道[16]. 这也是JPG格式图像比PNG格式图像占用空间更小的根本原因. 此外, 两种格式对数据均有压缩的算法. 这里不讨论并忽略两种格式本身的数据压缩算法.
在分离得到PNG格式图像的R、G、B、A这4个通道的数据矩阵后, 可对这4个2维数据矩阵分别作奇异值分解, 再根据使用的k取值的方法和阈值f, 可得到这4个数据矩阵的前k个特征值、
要查看压缩后的PNG格式图像, 则可将4个通道的前k个特征值、
这里以一张原图的PNG、JPG 2种格式为例, 用
使用的图像原图如图3所示.

|
图 3 原图 |
原图宽度为4928像素, 高度为3264像素, 用8位整数表示各通道的值. 则PNG原图占用的存储空间为(不考虑PNG格式本身的压缩效果):
| $ 4928\times 3264\times 4\times 8=514\;719\;744\;{\rm bits}\approx 61.36\; {\rm MB} $ |
JPG原图占用的存储空间为(不考虑JPG格式本身的压缩效果):
| $ 4928\times 3264\times 3\times 8=386\;039\;808\;{\rm bits}\approx 46.02\;{\rm MB}$ |
在Python中, 可用代码1的源代码获取PNG原图4个通道数据矩阵.
代码1. 获取PNG原图4通道数据矩阵
import numpy as np
from PIL import Image
#加载图像, 第1个参数为原图的完整路径
orignImage=Image.open(r'原图.png','r')
imageArray=np.array(orignImage)
#得到R通道数据矩阵
R=imageArray[:,:,0]
#得到G通道数据矩阵
G=imageArray[:,:,1]
#得到B通道数据矩阵
B=imageArray[:,:,2]
#得到A通道数据矩阵
#原图为JPG时应注释此句源代码
A=imageArray[:,:,3]
PIL为Python的一个第三方图像处理类库, 事先应在操作系统的命令界面用语句“pip install pillow”来安装.
3.2 按特征值个数占比阈值取特征值个数在Python中, 用代码2即可得到一个数据矩阵的奇异值分解结果.
代码2. 数据矩阵奇异值分解
import numpy as np
#对R通道数据矩阵作奇异值分解
U_R,sigma_R,V_T_R=np.linalg.svd(R)
#对G通道数据矩阵作奇异值分解
U_G,sigma_G,V_T_G=np.linalg.svd(G)
#对B通道数据矩阵作奇异值分解
U_B,sigma_B,V_T_B=np.linalg.svd(B)
#对A通道数据矩阵作奇异值分解
#为JPG原图时应注释此句源代码
U_A,sigma_A,V_T_A=np.linalg.svd(A)
可以发现, 在作奇异值分解后, sigma_R、sigma_G、sigma_B、sigma_A均为一维数组, 其元素个数均为3264, 则表明均有3264个特征值. 需要注意的是, Python中的0会表示为一个很小的值, 而不会表示为整型的0, 因此有的通道数据矩阵可能并没有3264个特征值, 需要编程判断, 可以用特征值与一个很小的值(如0.0001)比较, 如果小于这个很小的值, 则将特征时判断为0. 结果发现, sigma_A的特征值只有1个. 为什么会这样呢?说明A通道数据是冗余的.
设计一个函数, 用于生成指定的比例阈值下, 用通道的压缩后数据来生成图像的近似数据矩阵, 如代码3所示.
代码3. 指定比例阈值下的图像近似数据矩阵生成
#功能: 针对某个通道的数据矩阵作奇异值分解得到的U矩阵、sigma#数组、V_T矩阵, 根据percent(百分比)取前若干个特征值来生成#该通道的近似数据矩阵
#参数: U, 对某个通道的数据作矩阵奇异值分解后得到的U矩阵; sigma, #对某个通道的数据作矩阵奇异值分解后得到的sigma数组; V_T, 对#某个通道的数据作矩阵奇异值分解后得到的V_T矩阵; percent, 特#征值个数占比阈值.
#返回值: 图像的某个通道的近似数据矩阵
def genCompressData(U,sigma,V_T,percent):
m=U.shape[0]
n=V_T.shape[0]
reChannel=np.zeros((m,n))
for k in range(len(sigma)):
#以得到该通道的近似数据矩阵
#逐个累加
reChannel=reChannel+sigma[k]*np.dot(U[:,k].reshape(m,1),
V_T[k,:].reshape(1,n))
#如果已经超过设定的比例阈值
if (float(k)/len(sigma)>percent):
#将数据值规范到0-255范围内
reChannel[reChannel<0]=0
reChannel[reChannel>255]=255
break
#将返回的近似数据矩阵的元素数据类型规范
#为uint8
return np.rint(reChannel).astype("uint8")
取特征值个数占比阈值f分别为0.001、0.005、0.01、0.02、0.03、0.04、0.05、0.1. 可用代码4逐个形成并保存压缩后再生成的图像.
代码4. 形成并保存过程
for p in [0.001,0.005,0.01,0.02,0.03,0.04,_0.05,0.1]:
#生成R通道近似数据矩阵
reR=genCompressData(U_R,sigma_R,V_T_R,p)
#生成G通道近似数据矩阵
reG=genCompressData(U_G,sigma_G,V_T_G,p)
#生成B通道近似数据矩阵
reB=genCompressData(U_B,sigma_B,V_T_B,p)
#生成A通道近似数据矩阵, 为JPG原图时应注释此句源代码
reA=genCompressData(U_A,sigma_A,V_T_A,p)
#生成完整的近似数据3维矩阵, 原图为JPG时则转而使用下面的
#注释语句
reI=np.stack((reR,reG,reB,reA),2)
# reI=np.stack((reR,reG,reB),2)
reI=np.stack((reR,reG,reB,reA),2)
Image.fromarray(reI).save
("{}".format(p)+"img.png")
为简便起见, 取比例阈值f值为0.001、0.01、0.05、0.1时的4幅压缩效果图作出展示, 如图4所示. 从图中可以看出, 比例阈值f值为0.001图不清楚, 为0.01值时可以大致看出轮廓, 为0.05时图像基本可辨, 为0.1时图像与原图相差无几, 人眼分辨不出是否压缩过.
对JPG格式图像的实验结果这里不再重复罗列分析. 在计算出取不同的比例阈值下的压缩比后, 列出结果如表1所示.
从表1可以看到, 即使是取比例阈值f为0.1, 压缩比都还能达到5.99, 因此, 压缩效果良好. 如果对压缩后的图像清晰度要求可以降低, 则还可以得到更高的压缩比.
表1中的两种格式的图像的压缩比相同的原因是, 不管是3个通道还是4个通道, 在同一比例阈值下, 针对各个通道取特征值的个数相同, 故压缩比就会相同.

|
图 4 按特征值个数占比阈值取特征值个数时的压缩效果图 |
| 表 1 按特征值个数占比阈值取特征值个数时的压缩比(4个通道均相同) |
3.3 按特征值之和占比阈值取特征值个数
设计一个函数(代码5), 用于生成指定的比例阈值下, 用各通道的压缩后数据来生成图像的近似数据矩阵.
代码5. 图像近似数据矩阵生成
#功能: 针对某个通道的数据矩阵作奇异值分解得到的U矩阵、sigma#数组、V_T矩阵, 根据percent(百分比)取前若干个特征值来生成#图像的该通道的近似数据矩阵;
#参数: U, 对某个通道的数据做矩阵奇异值分解后得到的U矩阵; #sigma, 对某个通道的数据作矩阵奇异值分解后得到的sigma数组; #V_T, 对某个通道的数据作矩阵奇异值分解后得到的V_T矩阵;
#percent, 特征值之和占比阈值.
#返回值: 图像的该通道的近似数据矩阵
def genCompressDataFromSum(U,sigma,V_T,percent):
m=U.shape[0]
n=V_T.shape[0]
reChannel=np.zeros((m,n))
sum=0.0 #sum为特征值总和
for i in sigma:
sum+=i
# sumcurrent为已累加的特征值的和
sumcurrent=0.0
for k in range(len(sigma)):
#逐个累加, 以得到该通道的近似数据矩阵
reChannel=reChannel+sigma[k]*np.dot
(U[:,k].reshape(m,1),V_T[k,:].reshape(1,n))
#累加特征值
sumcurrent+=sigma[k]
#如果已经超过设定的比例阈值
if (sumcurrent/sum>percent):
#将数据值规范到0-255范围内
reChannel[reChannel<0]=0
reChannel[reChannel>255]=255
break
#将返回的近似数据矩阵的元素数据类型规范为uint8
return np.rint(reChannel).astype("uint8")
取特征值之和占比阈值f分别为0.5、0.6、0.7、0.8、0.9, 可用代码6逐个形成并保存压缩后再生成的图像.
代码6. 形成并保存过程
for p in[0.3,0.4,0.5,06,0.7,0.8,0.85,0.9]:
#生成R通道近似数据矩阵
reR= genCompressDataFromSum(U_R,sigma_R,V_T_R,p)
#生成G通道近似数据矩阵
reG= genCompressDataFromSum(U_G,sigma_G,V_T_G,p)
#生成B通道近似数据矩阵
reB= genCompressDataFromSum(U_B,sigma_B,V_T_B,p)
#生成A通道近似数据矩阵, 为原图JPG时应注释此句源代码
reA= genCompressDataFromSum(U_A,sigma_A,V_T_A,p)
#生成完整的近似数据3维矩阵, 原图为JPG时则转而使用下面的
#注释语句
reI=np.stack((reR,reG,reB,reA),2)
# reI=np.stack((reR,reG,reB),2)
#保存图像, 参数为图像的完整路径
Image.fromarray(reI).save
(“{}”.format(p)+“img.png”)
为简便起见, 取比例阈值f值为0.6、0.7、0.8、0.85时的4幅压缩效果图作出展示, 如图5所示. 可以看到, 当比例阈值f值为0.7时, 已基本可辨; 当比例阈值f值为0.85时, 图片已经比较清晰. 表2还给出了取不同的阈值f值时, 对应的各个通道的特征值个数, 以及针对PNG格式图像、针对JPG格式图像的存储空间和压缩比.
表2中PNG格式图像的存储空间和JPG格式图像的存储空间相同, 且A通道的k值为1的原因是, PNG格式图像原图的A通道中的值都是等值的255, 相当于这个通道的数据是冗余的, 其图片显示效果与JPG格式图像相当.

|
图 5 按特征值之和占比阈值取特征值个数时的压缩效果图 |
3.4 压缩比变化趋势分析
根据表1和表2, 作比例阈值和压缩比之间的关系图, 如图6所示.
从图6(a)来看, 对PNG格式图像的压缩比和对JPG格式图像的压缩比的变化曲线相同. 在比例阈值为0.01时出现曲线拐点, 这表明在前1%的特征值里, 较大值的特征值比较集中; 之后曲线变缓, 在比例阈值为0.1以后, 曲线已经非常平缓, 表明增加特征值已很难再改善图像质量.
从图6(b)来看, 对JPG格式图像的压缩比要比对PNG格式图像的压缩比低一点. 在比例阈值为0.9后, 曲线变得更为平缓, 这表明增加特征值已很难再改善图像质量.
| 表 2 按特征值之和占比阈值取特征值个数时的压缩比(通道R, G, B, A) |
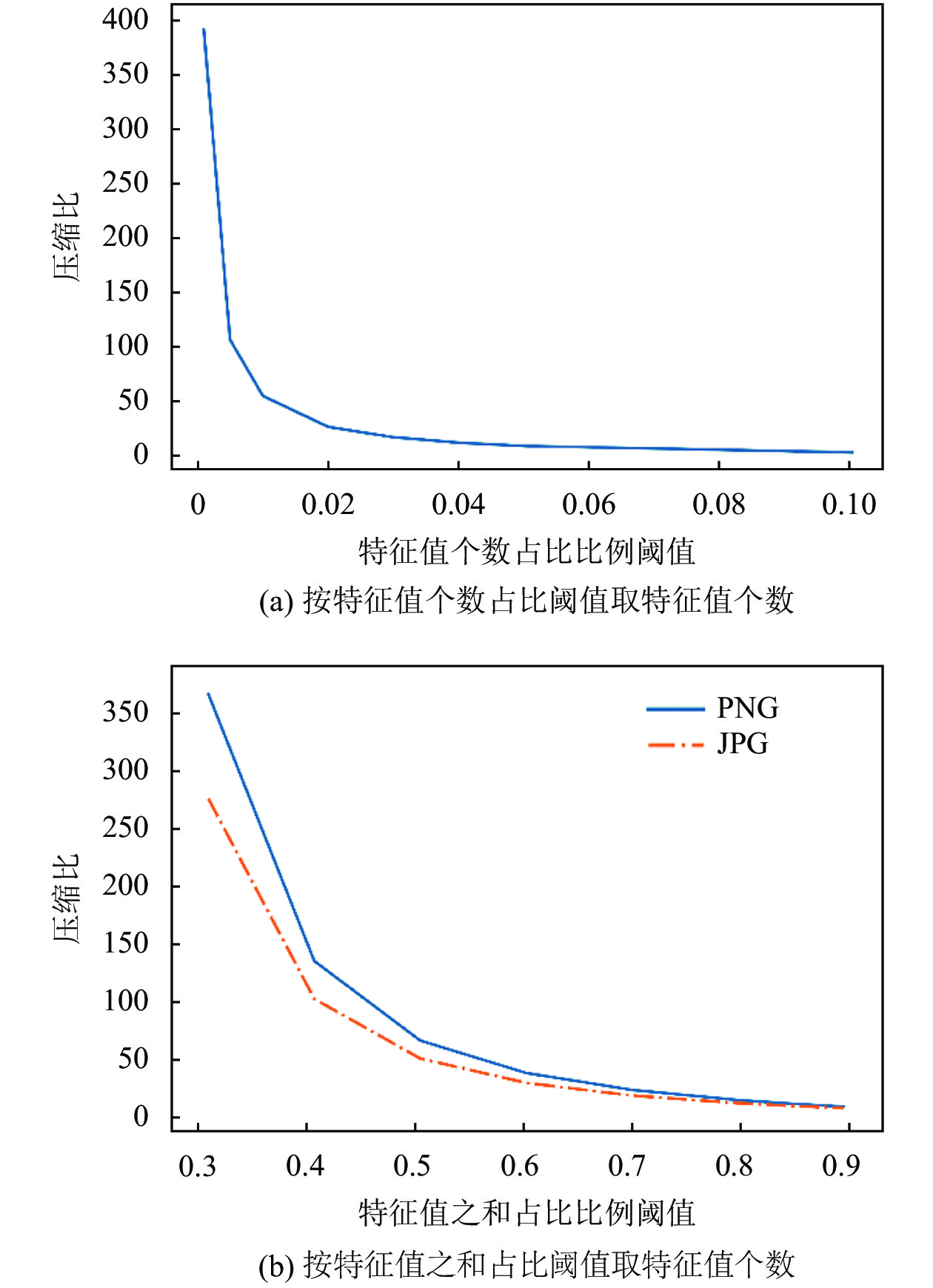
|
图 6 比例阈值和压缩比之间的关系图 |
相对来说, 按特征值之和占比阈值取特征值个数的方法更为实用. 因为首先, 它考虑的是特征值的重要程度, 而不是个数; 其次这种方法可以应对个别通道数据冗余的问题. 更为重要的是, 这种方法可以用于进行大规模数量的图像文件压缩, 因为这种方法可以划定一个统一的可以接受的特征值之和占比阈值, 这个阈值就直接代表着图像的清晰度. 鉴于前述对占比阈值的分析, 认为这个统一的占比阈值如要基本可辨取0.7, 如要比较清晰取0.85. 但按特征值个数占比阈值取特征值个数的方法不能划定一个统一的比例阈值, 因为在同一个阈值下, 不同的图像文件的清晰程度可能不同.
3.5 压缩算法对比分析现已有很多经典的图像压缩算法. 以经典的PNG[5]、JPG[6]图像格式为对比, 仍以本文的图片作为示例, 与本文的压缩方法在压缩比上的对比分析如表3所示. 由此可见, 在对PNG按特征值之和占比阈值取特征值个数(f=0.7)时可以取得最高的压缩比.
| 表 3 对不同图像格式处理算法的压缩比对比 |
鉴于各种算法的原理不同, Python已经提供了成熟的软件包PIL, 直接用保存功能即可将图片存储为JPG或PNG格式, 不便计算时间效率. 而本文给出的算法关键之处在于做奇异值分解所耗费的时间, 仍以本文的图片作为示例, 实验结果如表4所示. 可见, 对JPG做奇异值分解效率明显较高, 但显然处理一个图片已超过1分钟, 效率有待提升.
| 表 4 奇异值分解时间效率 |
4 结束语
通过奇异值分解, 可以得到3个分解结果, 即左奇异向量组成的标准正交基矩阵
本文研究的局限性在于仅限于奇异值分解本身并应用于图像压缩领域, 没有将奇异值分解和其它压缩算法相结合开展研究. 下一步的研究可结合包括奇异值分解在内的多种压缩算法提出新的组合算法, 并作大规模数量的图像文件处理实验、对比分析, 以寻求具有更高压缩比、能普适应用的图像压缩方法.
| [1] |
Mou J, Yang FF, Chu R, et al. Image compression and encryption algorithm based on hyper-chaotic map. Mobile Networks and Applications, 2019.
|
| [2] |
王棒. 基于压缩感知和极余弦变换的图像多功能双水印算法研究[硕士学位论文]. 西安: 西安理工大学, 2019.
|
| [3] |
Blasch E, Chen HM, Irvine JM, et al. Prediction of compression-induced image interpretability degradation. Optical Engineering, 2018, 57(4): 043108. |
| [4] |
Shapira D, Storer JA. In place differential file compression. The Computer Journal, 2005, 48(6): 677-691. DOI:10.1093/comjnl/bxh128 |
| [5] |
胡启杨. 基于压缩感知的视频监控图像处理算法研究[硕士学位论文]. 北京: 华北电力大学, 2018.
|
| [6] |
霍英海. 基于压缩感知的遥感影像融合技术研究[硕士学位论文]. 重庆: 重庆邮电大学, 2019.
|
| [7] |
Epps BP, Krivitzky EM. Singular value decomposition of noisy data: Mode corruption. Experiments in Fluids, 2019, 60(8): 121. DOI:10.1007/s00348-019-2761-y |
| [8] |
Allanki S, Dixit M, Thangaraj P, et al. Analysis and modelling of septic shock microarray data using Singular value decomposition. Journal of Biomedical Informatics, 2017, 70: 77-84. DOI:10.1016/j.jbi.2017.05.005 |
| [9] |
徐小敏. 超宽带穿墙雷达杂波抑制与成像方法研究[硕士学位论文]. 南京: 南京信息工程大学, 2019.
|
| [10] |
郭明军, 李伟光, 杨期江, 等. 基于SVD原理的PCA特征频率提取算法及其应用. 华南理工大学学报(自然科学版), 2020, 48(1): 1-9. |
| [11] |
Son D, Park Y. Generalization of head-related transfer function database using tensor-singular value decomposition. Noise Control Engineering Journal, 2017, 65(5): 454-461. DOI:10.3397/1/376561 |
| [12] |
张啸剑, 付聪聪, 孟小峰. 结合矩阵分解与差分隐私的人脸图像发布. 中国图象图形学报, 2020, 25(4): 655-668. DOI:10.11834/jig.190308 |
| [13] |
马敏, 何小芳, 李明, 等. 基于改进TSVD正则化的ECT图像重建算法. 传感器与微系统, 2020, 39(4): 136-139. |
| [14] |
杨智伟, 刘灏, 毕天姝, 等. 基于奇异值分解的PMU数据恢复法. 中国电机工程学报, 2020, 40(3): 812-821. |
| [15] |
Andono PN, Supriyanto C, Nugroho S. Image compression based on SVD for BoVW model in fingerprint classification. Journal of Intelligent & Fuzzy Systems, 2018, 34(4): 2513-2519. |
| [16] |
王俊. 基于SVD裁剪的深度神经网络压缩技术研究与实现[硕士学位论文]. 北京: 北京邮电大学, 2019.
|
 2021, Vol. 30
2021, Vol. 30


