随着网络信息技术的发展, 推荐系统被广泛应用到社交媒体网络、新闻推送、购物平台等领域. 根据实现思想不同, 推荐算法主要分为3类: 基于内容的推荐、基于协同过滤的推荐以及混合推荐方法^[1].

协同过滤^[2]作为应用最广泛的一种推荐算法, 其主要思想是由用户对商品的偏好发现用户之间的关联性, 基于关联性进行推荐, 即相似度高的用户往往有相似的偏好. 一般来讲, 协同过滤主要通过用户和商品的历史交互信息建模(如评分、点击率等), 并得到它们的嵌入表示. 如矩阵分解^[3]将用户和商品映射到同一维度的隐空间中, 并使用内积计算用户对商品的偏好程度. 近年来, 深度学习的发展进一步提高了推荐系统的性能. He等^[4]提出的NCF模型通过整合传统的矩阵分解和MLP进一步优化传统模型. Wang等^[5]提出的NGCF模型构建用户-商品的二部图, 通过图模型嵌入用户和商品的历史互动到特征向量中. 虽然这些方法提升了推荐系统的性能, 但是当用户和商品的数量增多, 推荐系统可能会面临据稀疏性和冷启动等问题, 从而无法实现个性化推荐.

近些年来, 异质信息网络^[6]由于包含多种类型的结点和边, 被广泛应用到各个领域中^[7-9]. 由于异质信息网络能表征丰富的辅助信息, 基于异质网的推荐算法被学者广泛研究. Sun等^[10]提出的PathSim基于元路径的相似性做推荐. Feng等^[11]提出的OptRank基于异质信息解决社交推荐系统的冷启动问题. Yu等^[12]基于异质网实体间的关系, 进一步优化推荐算法. Shi等^[13]将随机游走得到的异质信息与传统的矩阵分解模型做融合. 这些方法通过异质信息网络中的辅助信息, 得到了用户和商品的潜在特征, 但是可能会忽略用户和商品的历史互动等信息.

针对以上问题, 本文提出了基于融合元路径的图神经网络协同过滤算法. 该算法基于NGCF^[4]模型, 首先构建用户和商品的二部图, 将它们的历史互动嵌入到特征向量中, 然后通过神经网络多层传播获取用户和商品的高阶表示. 异质信息网络中不仅有用户和商品两种类型的结点, 还存在其他的结点类型和边类型, 这些节点会影响到用户和商品的表征. 为充分利用异质网络中的语义信息, 在模型的基础上引入元路径获取潜在的信息. 而不同的元路径往往有不同的含义, 得到多条元路径的潜在特征后, 引入融合函数及权重对多条元路径的信息有效融合. 总结来说, 本文的主要贡献可概括为以下3点:

(1)在图神经网络协同过滤算法中引入元路径, 基于元路径的随机游走生成用户和商品的潜在特征, 并引入融合函数及权重对多条元路径的表征融合.

(2)将图神经网络生成的高阶特征与异质网中元路径生成的潜在特征有效融合, 并做评分预测.

(3)在公开数据集Yelp、Amazon Book和Amazon Movie数据集上做实验, 并与传统算法比较, 验证了算法的有效性.

1 基本概念

定义1. 异质信息网络(heterogeneous information network)^[14]. 异质信息网络可表示为 $G = (V,E)$ , 其中V表示节点的集合, E表示边的集合. 对于每一个结点存在一种映射关系 $\phi :V \to A$ , 对于每一条边存在一种映射关系 $\varphi :E \to R$ , A和R分别代表结点类型和边类型, 且 $|A| + |R| > 2$ .

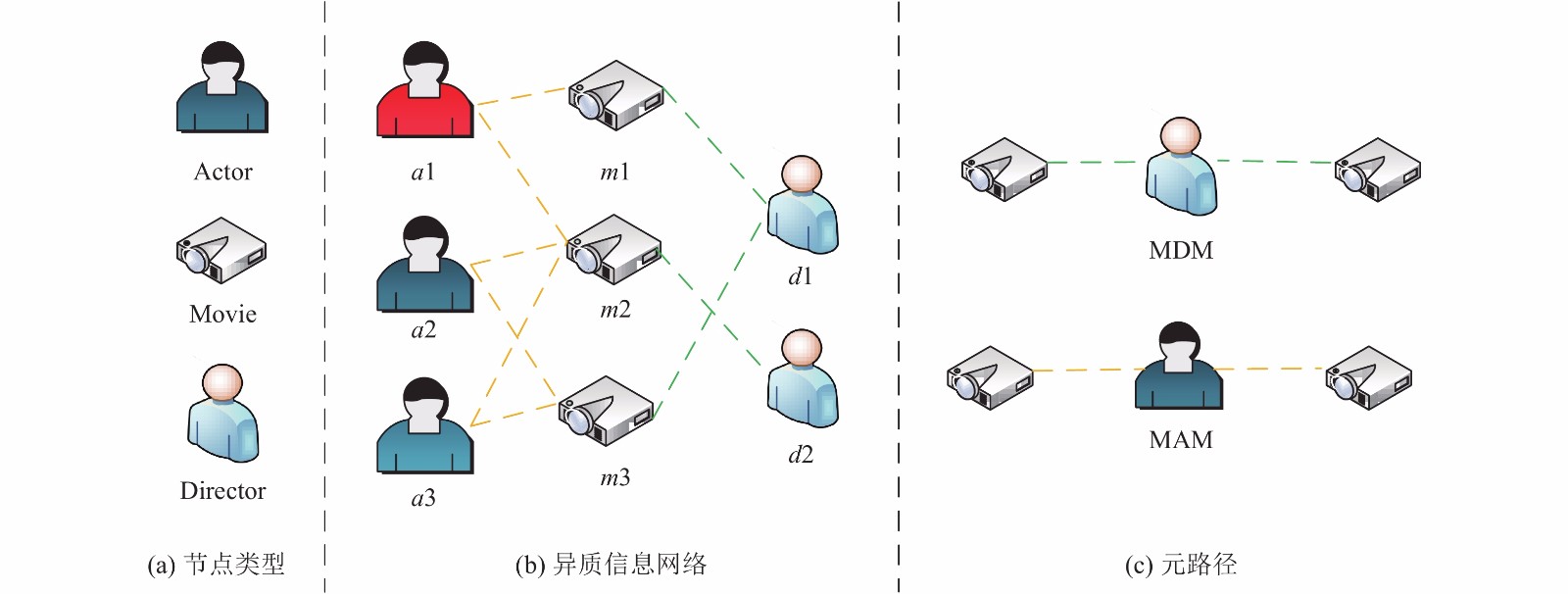
如图1(b)所示表示的是IMDB数据集构成的异质信息网络. 如图1(a)所示, 该异质网络有3种类型的节点, 分别是演员、电影和导演. 同时有两种类型的边, 分别是演员和电影之间的关系以及电影和演员之间的关系.

定义2. 网络模式(network schema)^[15]. 对于给定的网络 $G = (V,E)$ , V表示结点的集合, E表示边的集合, 且有映射关系 $\phi :V \to A$ 和 $\varphi :E \to R$ , 定义其网络模型为 ${{\cal T}_G} = (A,R)$ .

在异质信息网络中不同类型的实体间的关系可以用元路径表示.

定义3. 元路径(meta-path)^[16]. 给定网络模型 ${{\cal T}_G} = (A,R)$ , 元路径可定义连接多种结点类型的一组关系, 具体形式为 $P = {A_1}\mathop \to \limits^{{R_1}} {A_2}\mathop \to \limits^{{R_2}} \cdots {A_t}\mathop \to \limits^{{R_t}} {A_{t + 1}} \cdots \mathop \to \limits^{{R_l}} {A_{l + 1}}$ , 其中 ${R_i}$ 表示结点间的关系.

如图1(c)中列举了两条元路径, 分别是MDM和MAM. 这两条元路径有不同的语义信息, 其中MDM代表同一导演编导了不同的电影, 而MAM代表了同一演员出演了不同的电影. 为了更丰富的表征异质网中的信息, 我们在获取电影的特征向量时, 会赋予这两条元路径不同的权重.

2 融合元路径的图神经网络协同过滤算法

这部分主要介绍基于融合元路径的图神经网络协同过滤模型. 第一阶段基于NGCF^[4]框架先构建二部图, 将用户和商品的历史互动嵌入到特征向量中, 并通过神经网络传播. 异质信息网络中包含多种类型的节点和边. 为了更丰富的表征用户和商品, 在第二阶段通过元路径的随机游走获取用户和商品的低维表征, 并将多条元路径的潜在特征有效融合. 第三阶段将用户和商品的低维表征与高阶特征融合并做评分预测.

2.1 图神经网络协同过滤

从用户和商品的向量点积中很容易看出用户对商品的偏好程度. 传统推荐算法, 如矩阵分解等没有将交互信息嵌入到特征向量中, 只是用ID等属性初始化向量, 用交互信息优化模型. 为了从用户和商品的历史互动获取二者的高阶特征, 在本文中我们采用NGCF模型. 该模型主要分为3层: 输出层、嵌入层和传播层.

2.1.1 嵌入层

嵌入层将输入的稀疏向量转化为稠密向量, 随机初始化用户和商品的向量矩阵 ${{E}} \in {\mathbb{R}^{(M + N) \times d}}$ , 如式(1)所示, 其中用户数量为M, 商品数量N, d为表示维度的大小.

${{E}} = [\underbrace {{{{e}}_{{u_1}}}, \cdots ,{{{e}}_{{u_{{M}}}}}}_{},\underbrace {{{{e}}_{{i_1}}}, \cdots ,{{{e}}_{{i_{{N}}}}}}_{}]$

(1)

2.1.2 传播层

根据用户和商品的邻接矩阵, 将特征向量与其邻居节点向量融合, 然后通过多层神经网络进行信息传递得到最终的特征向量.

对于用户商品的任一结点对(u, i), 定义从商品i到用户u的信息传递函数为式(2)所示. 其中 ${{{e}}_{{i}}}$ 为商品的特征向量, ${{{e}}_u}$ 为用户的特征向量, $ 1/\sqrt{\left|{N}_{i}\Vert {N}_{u}\right|}$ 为用户u和商品i之间的权重系数, ${N_u}$ 和 ${N_i}$ 分别代表用户和商品的邻居结点个数, ${{{W}}_1},{{{W}}_2} \in {\mathbb{R}^{d' \times d}}$ 是权重矩阵参数, $ \odot $ 为向量对应元素之间的乘积.

${{{m}}_{u \leftarrow i}} = \frac{1}{{\sqrt {\left| {{N_i}} \right|\left| {{N_u}} \right|} }}\left( {{{{W}}_1}{{{e}}_i} + {{{W}}_2}\left( {{{{e}}_i} \odot {{{e}}_u}} \right)} \right)$

(2)

式(2)是针对一个邻居节点的表示, 由于用户的邻居节点可能有多个, 故用户最终的向量表示是其所有邻居结点的融合. 通过 $l$ 层的信息传递, 用户可以获得其 $l$ 阶邻居的信息, 第 $l$ 层的特征向量表示为式(3)所示. 从中可以看出信息传递过程中用户不仅融合了其邻居结点商品的特征, 而且保留了用户本身的特征.

${{e}}_u^{(l)} = {{LeakyReLU}}\left( {{{m}}_{u \leftarrow u}^{(l)} + \sum\limits_{i \in {{{N}}_u}} {{{m}}_{u \leftarrow i}^{(l)}} } \right)$

(3)

式中, ${{m}}_{u \leftarrow u}^{(l)}$ 和 ${{m}}_{u \leftarrow {{i}}}^{(l)}$ 的表示分别为式(4)和式(5)所示. 其中 ${p_{ui}}$ 是权重系数, ${{{W}}_1}$ 和 ${{{W}}_2}$ 为矩阵参数, ${{e}}_i^{(l - 1)}$ 是第 $l - 1$ 层商品的特征向量, ${{e}}_{{u}}^{(l - 1)}$ 是第 $l - 1$ 层用户的特征向量.

${{m}}_{u \leftarrow i}^{(l)} = {p_{ui}}\left( {{{W}}_1^{(l)}{{e}}_i^{(l - 1)} + {{W}}_2^{(l)}\left( {{{e}}_i^{(l - 1)} \odot {{e}}_u^{(l - 1)}} \right)} \right)$

(4)

${{m}}_{u \leftarrow u}^{(l)} = {{W}}_1^{(l)}{{e}}_u^{(l - 1)}$

(5)

经过 $l$ 层传播得到用户向量表示可为集合 ${E_u} = \left\{ {e_u^{(0)},} \right. $ $\left. {e_u^{(1)}, \cdots ,e_u^{(l - 1)},e_u^{(l)}} \right\}$ , 商品向量可表示为 ${E_i} = \left\{ {e_i^{(0)},{e_i^{(1)}, \cdots ,}} \right. $ $\left. {e_i^{(l - 1)},e_i^{(l)}} \right\}$ . 用户和商品的特征向量最终表示为式(6)所示, 其中 $ \Vert $ 表示向量之间的拼接.

$ {e}_{u}^{*}={e}_{u}^{(1)}\Vert \cdots \Vert {e}_{u}^{(l)},{e}_{i}^{*}={e}_{i}^{(1)}\Vert \cdots \Vert {e}_{i}^{(l)}$

(6)

2.2 异质信息网络中的低维表征 2.2.1 元路径的随机游走

对于DeepWalk^[16]和Node2Vec^[17]采用的是随机游走生成网络中的节点序列, 这种方式的随机游走会偏向于节点类型多的节点. 为了解决这个问题, Dong等^[18]提出的Metapath2Vec基于元路径的随机游走, 能更好的涵盖异质网中丰富的语义信息. 首先基于元路径进行随机游走生成节点序列, 然后采用Skip-gram学习异质网中的低维表征.

对于给定的元路径 ${A_1}\mathop \to \limits^{{R_1}} {A_2}\mathop \to \limits^{{R_2}} \cdots {A_t}\mathop \to \limits^{{R_t}} {A_{t + 1}} \cdots \mathop \to \limits^{{R_l}} {A_{l + 1}}$ , ${A_i}$ 表示节点类型, 设第 $i$ 个节点 $V_t^i$ 的类型为 ${A_i}$ , 则第 $i + 1$ 个游走节点 ${v^{i + 1}}$ 的选择概率如式(7)所示. 其中第 $i$ 个节点类型为 ${A_{t + 1}}$ , ${N_{t + 1}}(V_t^i)$ 表示 $V_t^i$ 的邻居节点中所有类型为 ${A_{t + 1}}$ 的节点个数. 该公式表示只有下一个节点为meta-path上指定类型的节点时才游走, 且游走的概率为指定类型节点个数的倒数, 直至游走序列到达指定长度.

$s\left( {{v^{i + 1}}\left| {v_t^i,P} \right.} \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{{\left| {{N_{t + 1}}\left( {v_t^i} \right)} \right|}} },&{\left( {{v^{i + 1}},v_t^i} \right) \in E,\; \Phi \left( {{v^{i + 1}}} \right) = {A_{t + 1}}} \\ 0,&{\left( {{v^{i + 1}},v_t^i} \right) \in E, \Phi \left( {{v^{i + 1}}} \right) \ne {A_{t + 1}}} \\ 0,&{\left( {{v^{i + 1}},v_t^i} \right) \notin E} \end{array}} \right.$

(7)

在得到随机游走的节点序列后, 由于我们关注的用户和商品的低维表征, 所以进行节点类型限制和过滤^[13]. 具体来说, 只选择以用户、商品类型节点为起点的节点序列. 并且在每条序列中, 只保留与起点类型相同的节点, 对其他类型的节点过滤. 例如, 对于元路径MDM我们可能游走出序列 ${u_1} \to {m_1} \to {u_2} \to {m_2} \to {u_3} \to {m_2} \to {u_4}$ , 对节点过滤得到 ${u_1} \to {u_2} \to {u_3} \to {u_4}$ .

通过Skip-gram模型学习异质网中节点的低维表征, 优化函数如式(8)所示. 其中 ${N_t}$ 表示顶点为v的邻居节点中类型为t的集合.

$ \underset{\theta }{\mathrm{max}}{\displaystyle \sum _{v\in V}{\displaystyle \sum _{t\in {T}_{v}}{\displaystyle \sum _{{c}_{t}ϵ{{\rm N}}_{t}}{s}_{t}}}}\mathrm{log}{\rm P}\left({{\cal C}}_{t}\mid v;\theta \right)$

(8)

2.2.2 低维表征融合

对于给定的节点 $v$ , 其元路径对应的表征集合为 $\left\{ {{{e}}_v^{(0)},{{e}}_v^{(1)}, \cdots ,{{e}}_v^{(p - 1)},{{e}}_v^{(p)}} \right\}$ , 其中p为元路径的个数. 现有的表征融合往往采用简单的线性的融合方式, 即赋予每条元路径一个权重, 这可能会造成表征质量降低. 在本文中我们在权重的基础上引入融合函数, 融合公式如式(9)所示. 其中 $w_u^{(i)}$ 为第 $i$ 个元路径的权重, ${{{M}}^{(i)}} \in {\mathbb{R}^{{{D}} \times d}}$ 为权重矩阵, ${{{b}}^{(i)}} \in {\mathbb{R}^{{D}}}$ 为权重参数.

${{g}}\left( {\left\{ {{{e}}_u^{(i)}} \right\}} \right) = \sum\limits_{i = 1}^{|p|} {w_u^{(i)}} \left( {{{{M}}^{(i)}}e_u^{(i)} + {{{b}}^{(i)}}} \right)$

(9)

2.3 模型预测

在2.1节中通过图神经网络得到了用户和商品的高阶向量表示, 2.2节中通过元路径得到了用户和商品潜在的特征, 模型最终预测为式(10)所示. 其中 ${{{e}}_u}$ 及 ${{{e}}_i}$ 是通过图神经网络得到的特征向量, ${{{{\textit{z}}}}_u}$ 及 ${{{{\textit{z}}}}_i}$ 是由元路径得到的潜在向量, $\alpha $ 为权重参数.

$\widehat {{r_{u,i}}} = {{e}}_u^{\rm{T}} \cdot {{{e}}_i} + \alpha \cdot {{{\textit{z}}}}_u^{\rm{T}} \cdot {{{{\textit{z}}}}_i}$

(10)

2.4 模型优化

为了更好地将高阶特征与潜在向量融合起来, 我们采用式(11)所示的函数优化. 其中 ${r_{u,i}}$ 表示用户和商品的实际分数, ${r_{u,i}}^\prime $ 是预测分数, ${{{e}}_u}$ 及 ${{{e}}_i}$ 是通过图神经网络得到的特征向量, ${{{{\textit{z}}}}_u}$ 及 ${{{{\textit{z}}}}_i}$ 是由元路径得到的潜在向量, $\lambda $ 为权重参数, ${\Theta ^{(U)}}$ 及 ${\Theta ^{(I)}}$ 分别表示模型中用户和商品对应的参数.

$ \begin{split} {\cal L} =& \displaystyle\sum\limits_{\left( {u,i,{r_{u,i}}} \right) \in {\cal R}} {\left[ {{{\left( {{r_{u,i}} - {r_{u,i}}^\prime } \right)}^2}{\rm{ + }}} \right.} \lambda \displaystyle\sum\limits_{\left( {u,i} \right)} {\left.\Big( {{{\left\| {{{{e}}_u}} \right\|}_2} + {{\left\| {{{{e}}_i}} \right\|}_2}} \right.} \\ &+\left. {\left. { {{\left\| {{{{{\textit{z}}}}_u}} \right\|}_2} + {{\left\| {{{{{\textit{z}}}}_i}} \right\|}_2} + {{\left\| {{\Theta ^{(U)}}} \right\|}_2} + {{\left\| {{\Theta ^{(I)}}} \right\|}_2}} \right) } \right] \\ \end{split} $

(11)

3 实验结果与分析

通过在Yelp、Douban book及Douban movie 3个数据集上做实验, 实验结果表明均方根误差都小于传统模型, 证明了算法的有效性.

3.1 数据集

为了证明算法的有效性, 选取了3个不同领域的数据集. Yelp是商务类型的数据, 稀疏度为0.08%. Douban book是书籍类型的数据, 稀疏度为0.27%. Douban movie是电影类型的数据, 稀疏度为0.63%. 3种数据集的具体信息如表1所示.

在获取用户及商品的潜在特征向量阶段会使用到元路径, 对于3种数据集我们使用的元路径如表2所示. 以Yelp数据集为例, 用户在神经网络传播层部分通过用户和物品的交互可以得到UBU, 同理物品在神经网络传播层部分通过物品和用户的交互可以得到BUB的路径, 所以在元路径中不再使用这两条元路径. Douban movie和Douban book的元路径中采用同样的思想.

3.2 评价指标

在本文中采用均方根误差(RMSE)评价推荐模型, 均方根误差是均方误差的算数平方根. 均方误差指的是参数估计值和参数真实值之差平方的期望值. 其中均方根误差值越小, 推荐模型的效果越好, 预测越精确. 它的表示如式(12)所示. 其中 ${D_{{\rm{test}}}}$ 表示测试集数据, ${r_{u,i}}$ 和 ${r_{u,i}}^\prime $ 分别表示结点对 ${\rm{(}}u{\rm{, }}i{\rm{)}}$ 的实际分数和模型的预测分数.

${{RMSE}} = \sqrt {\frac{1}{{\left| {{D_{{\rm{test}}}}} \right|}}\sum\limits_{(i,j) \in {D_{{\rm{test}}}}} {{{\left( {{r_{u,i}} - {r_{u,i}}^\prime } \right)}^2}} } $

(12)

3.3 方法对比

为了验证算法的有效性, 采取以下模型作为对比:

(1) HeteMF^[12]: 基于异质网中元路径的相似性做推荐.

(2) SoMF^[19]: 基于社交网络的推荐模型, 提出了具有社会正则化的矩阵分解模型.

(3) SemRec^[20]: 基于协同过滤的思想, 在加权异质信息网络中考虑不同元路径之间用户和商品的相似度做推荐.

3.4 实验结果及分析 3.4.1 确定训练集比例

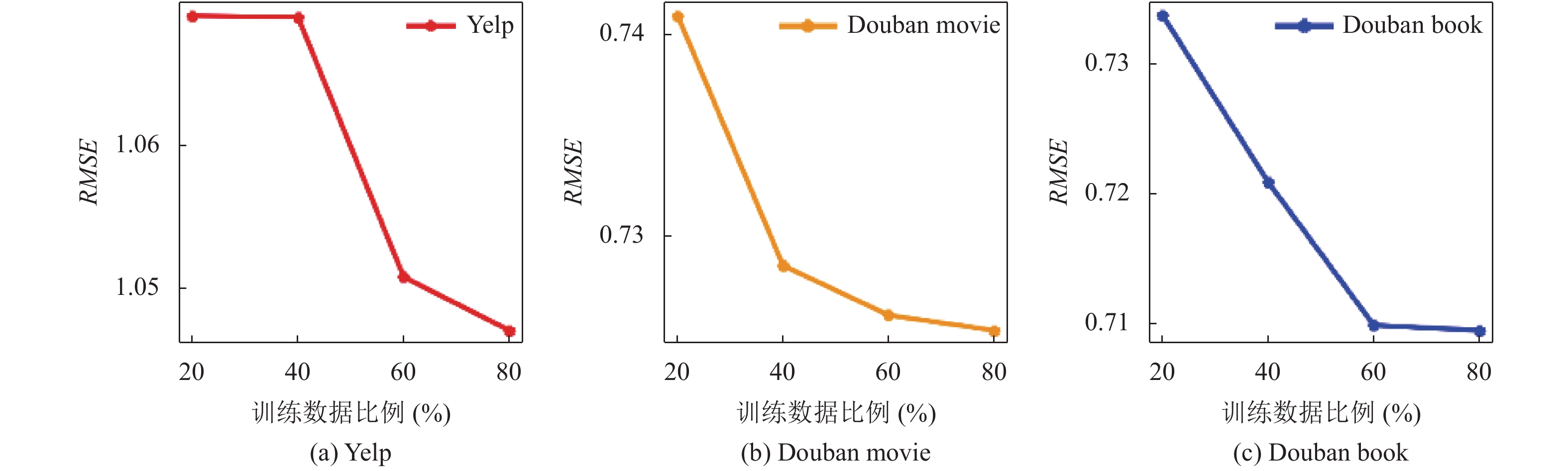
通过改变训练集与测试集的比例, 测试模型在不同比例下RMSE的值. 对于Yelp数据, 由于比较稀疏将训练集数据的比例设为{90%, 80%, 70%, 60%}, 而对于Douban movie和Douban book将训练集数据的比例设为{80%, 60%, 40%, 20%}, 实验结果如图2所示, 从左到右分别为Yelp、Douban movie及Douban book的实验结果. 从图2中可以看出Yelp数据在训练集数据占90%时RMSE达到最好的结果; Douban movie及Douban book数据在训练集数据占80%时RMSE达到最好的结果. 所以我们将Yelp的训练集和测试集的比例设为9:1, 而Douban movie及Douban book的训练集和测试集的比例设为8:2.

3.4.2 用户和商品的历史互动

在模型最后的预测中既考虑了用户和商品的高阶历史互动, 又考虑了异质信息网络中用户和商品的潜在语义信息. 为了证明模型的有效性, 将分别讨论用户和商品的历史互动及异质网中的语义信息对RMSE结果的影响.

在这个部分只保留用户和商品的历史互动, 而不考虑异质信息网络中用户和商品的潜在的语义信息. 在3种数据集上分别实验, RMSE值的结果如表3所示.

3.4.3 异质信息网络中的语义信息

在这个部分只保留异质信息网络中用户和商品的潜在语义信息, 而不考虑用户和商品的历史互动的信息. 同时在原有的元路径基础上, 加上用户和物品的交互. 在3种数据集上分别实验, RMSE值的结果如表4所示.

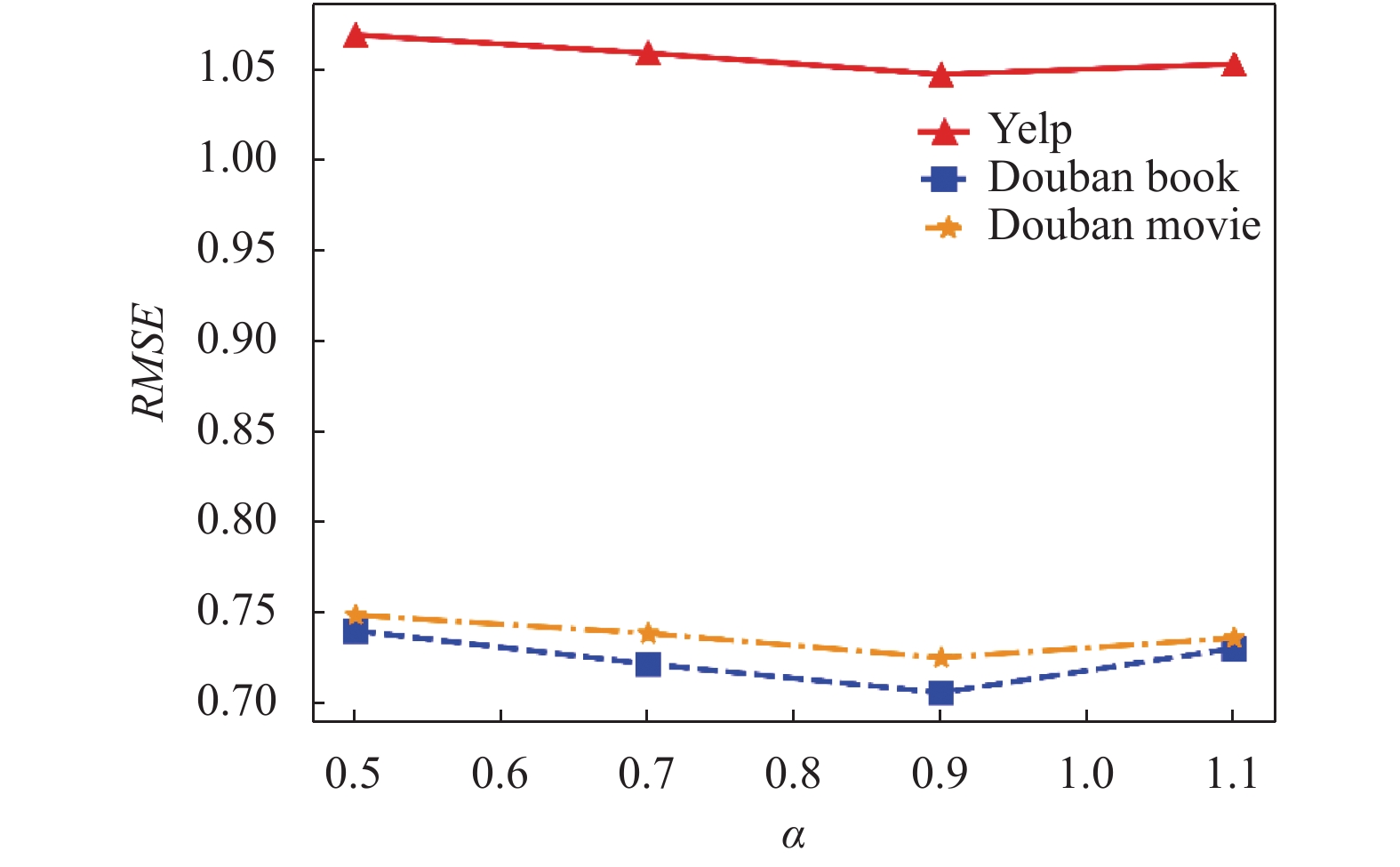
3.4.4 预测函数中的权重系数

我们通过调整预测函数中的权重参数 $\alpha $ , 研究这个权重参数时如何影响模型性能的. 选定参数 $\alpha $ 的值在集合{0.5,0.7,0.9,1.1}间调整. 实验结果如图3所示, 从图中可以看出RMSE的值随着 $\alpha $ 的增大先下降后上升, 在0.9时RMSE达到最小值.

3.4.5 实验结果与分析

3种数据集在不同模型上的实验结果如表5所示, 表中的数字代表实验结果RMSE的值. 由实验结果可知, 基于融合元路径的图神经网络协同过滤算法比传统的推荐算法有一定提高. 同时与表3中只考虑用户和商品的历史互动以及表4中只考虑异质信息网络中的潜在语义信息的结果相比, 融合元路径的图神经网络模型的RMSE值更小. 本模型通过图神经网络模型既考虑了用户和商品的历史互动, 又通过元路径考虑了异质信息网络中的语义信息, 并将两者有效的融合起来, RMSE值更小, 推荐效果更好.

4 结论与展望

本论文通过分析传统推荐算法的缺点, 提出了基于融合元路径的图神经网络协同过滤算法. 该算法既考虑了异质信息网络中的语义信息, 通过元路径获取潜在的信息, 并引入融合函数和权重对多条元路径的表征融合, 避免了冷启动及数据稀疏等问题. 同时又充分利用了用户和商品的历史互动, 通过二部图嵌入用户和商品的特征, 图神经网络的多层传播得到高阶向量. 本论文还与传统的推荐算法对比, 证明了模型的有效性. 在未来的工作中, 我们将进一步优化元路径的融合方式, 将注意力机制^[21]引入元路径中, 获取异质信息网络中更精准的语义信息.