爬壁机器人由于其可以在高空作业的特殊性广泛应用于船舶喷漆除锈、油罐检测等行业^[1,2]. 其中履带式磁吸附爬壁机器人作为一种较为常见的爬壁机器人, 是典型的非线性多输入多输出系统. 在壁面爬行过程中履带机器人容易受到重力及外部干扰等因素影响, 从而导致机器人实际位姿与理想位姿的误差. 为了解决这一问题, 文献[3,4]只从机器人运动学出发设计控制PID、反演控制等算法, 但这没有考虑机器人的动力特性, 在实际运用中其控制算法具有一定的局限性且对外部干扰的抑制效果较差. 因此, 很多学者结合运动学和动力学进行研究, 并利用模糊控制、神经网络控制、鲁棒自适应控制等算法进行轨迹跟踪控制^[5–8], 智能算法能呈现出较好的跟踪效果并抑制外界干扰, 但算法比较复杂, 实用性与实时性不高.

本文参考轮式机器人的研究及爬壁机器人运动的特点, 受文献[9]启发在研究爬壁机器人运动学与动力学的基础上对控制算法上进行改进. 本文将建模误差与外部干扰作为系统的总体扰动, 通过改进型非线性干扰观测器^[10]对该扰动进行观测作为前馈控制, 使扰动误差以指数形式收敛, 并采用反演控制作为运动学控制, 采用滑模反演控制作为动力学控制, 使动力学控制算法收敛速度快于运动学算法收敛速度, 避免造成闭环系统的不稳定. 最后使用Lyapunov方法验证了系统的稳定性. 仿真结果验证了该算法的有效性.

1 履带式爬壁机器人模型

根据爬壁机器人的机械结构及工作环境特点, 做出以下假设:

(1) 在平直二维壁面内工作;

(2) 爬壁机器人为刚体, 且质量分布均匀, 其重心与几何中心重合;

(3) 理想滚动条件, 爬壁机器人无滑移, 运动瞬时方向即机器人本体坐标系X'轴方向.

根据以上假设, 本文研究的履带式机器人运动模型可简化为图1所示.

1.1 运动学模型

履带式爬壁机器人实现转向运动主要有给予两轮相反速度和给予两轮方向相同但大小不同速度两种方法, 本文采用第二种方法. $\left( {X,Y} \right)$ 为爬壁机器人在全局坐标系XOY下的质心坐标; $\left( {X',Y'} \right)$ 为机器人本体坐标系X'O'Y'中的坐标; $\theta $ 为机器人运动方向与X轴的夹角, 其中 $\theta $ 的范围为 $ \left[0, 2\pi \right)$ ; $({\omega _L},{\omega _R})$ 为爬壁机器人的左右轮角速度, 即爬壁机器人的输入控制量; R为机器人车轮半径; L为车身宽度. 那么机器人位姿可用 $q = {\left[ {\begin{array}{*{20}{c}} X&Y&\theta \end{array}} \right]^{\rm{T}}}$ 来表示机器人的运动学方程表示为:

$ \begin{split} \dot q =& \left[ {\begin{array}{*{20}{c}} {\dot X} \\ {\dot Y} \\ {\dot \theta } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{v_x}} \\ {{v_y}} \\ \omega \end{array}} \right] \\ =& R*\left[ {\begin{array}{*{20}{c}} {\dfrac{{\cos \theta (t)}}{2}}&{\dfrac{{\cos \theta (t)}}{2}} \\ {\dfrac{{\sin \theta (t)}}{2}}&{\dfrac{{\sin \theta (t)}}{2}} \\ { - \dfrac{1}{L}}&{\dfrac{1}{L}} \end{array}} \right] * \left[ {\begin{array}{*{20}{c}} {{\omega _L}} \\ {{\omega _R}} \end{array}} \right] \\ \end{split} $

(1)

其中, ${v_x}$ 为机器人速度在X轴方向的分量, ${v_y}$ 为机器人速度在Y轴方向的分量.

又有:

$ \eta = \left[ {\begin{array}{*{20}{c}} v \\ \omega \end{array}} \right] = R*\left[ {\begin{array}{*{20}{c}} {\dfrac{1}{2}}&{\dfrac{1}{2}} \\ { - \dfrac{1}{L}}&{\dfrac{1}{L}} \end{array}} \right]*\left[ {\begin{array}{*{20}{c}} {{\omega _L}} \\ {{\omega _R}} \end{array}} \right] $

(2)

其中, $v$ 为质心速度, $\omega $ 为质心角速度. 为方便控制, 将式(2)代入式(1), 状态方程简化为:

$ \dot q = \left[ {\begin{array}{*{20}{c}} {\dot X} \\ {\dot Y} \\ {\dot \theta } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta (t)}&0 \\ {\sin \theta (t)}&0 \\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} v \\ \omega \end{array}} \right] = S(q)\eta $

(3)

此时控制量变为 $v$ 、 $\omega $ , 机器人满足非完整约束条件:

$ \dot X\sin \theta - \dot Y\cos \theta = 0 $

(4)

即系统约束向量 $A(q){\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\sin \theta }&{ - \cos \theta }&0 \end{array}} \right]$ .

1.2 动力学模型

针对履带爬壁机器人的瞬态动力学进行研究, 根据文献[11,12], 假设两侧履带受到的摩擦力相同, 将机器人模型简化如图2所示. 那么根据牛顿力学对机器人系统进行动力学分析, 当无外界干扰时, 对于机器人本体坐标系有:

$ \left\{ \begin{gathered} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! m\ddot X' = {F_L} + {F_R} - 2{F_{fx}} - {G_{x'}} \\ \;\;\; = {F_L} + {F_R} - 2{F_{fx}} - mg\sin \theta \\ m\ddot Y' = 2{F_{fy}} - {G_{y'}} = 2{F_{fy}} - mg\cos \theta \\ \!\!\!\!\!\!\!\!\!\!\!\!\! {I_c}\ddot \theta = ({F_R} - {F_L})*L/2 - 2{\rm{*}}{M_f} \\ \end{gathered} \right. $

(5)

其中, ${F_R} = {\tau _R}/r$ , ${F_L} = {\tau _L}/r$ , ${\tau _R}$ 、 ${\tau _L}$ 分别为左右电机驱动力矩, $r$ 为履带车轮半径; $m$ 为履带式爬壁机器人本体质量; ${I_c}$ 为机器人本体对质心的转动惯量; ${F_{fx}}$ 为单侧履带纵向摩擦力; ${F_{fy}}$ 为单侧履带横向摩擦力; ${M_f}$ 为单侧履带摩擦阻力矩.

将动力学方程从本体坐标系转化为全局坐标系可得:

$ \left\{ \begin{split} m\ddot X =& \left( {{F_L} + {F_R}} \right)\cos \theta \\ &-2({F_{fx}}\cos \theta + {F_{fy}}\sin \theta ) \\ m\ddot Y =& \left( {{F_L} + {F_R}} \right)\sin \theta \\ &-2({F_{fx}}\sin \theta - {F_{fy}}\cos \theta ) - G \\ {I_c}\ddot \theta =& ({F_R} - {F_L})L/2 - 2{M_f} \\ \end{split} \right. $

(6)

由以上公式可知, 当加入未知有界外部干扰时, 简化的爬壁机器人动力学方程用标准拉格朗日动力学模型可表示为:

$ M(q)\ddot q + V(q,\dot q)q + G(q) + {\tau _d} = B\tau + {A^{\rm{T}}}(q)\lambda $

(7)

其中, $M(q) = \left[ {\begin{array}{*{20}{c}} m&0&0 \\ 0&m&0 \\ 0&0&{{I_c}} \end{array}} \right]$ ; $V(q,\dot q) = {\left[ {\begin{array}{*{20}{c}} 0&0&0 \end{array}} \right]^{\rm{T}}}$ 为向心力和哥氏力矩阵; ${A^{\rm{T}}}(q)$ 为系统约束向量的转置; $G(q) = \left[ {\begin{array}{*{20}{c}} {2({F_{fx}}\cos \theta + {F_{fy}}\sin \theta )} \\ {2({F_{fx}}\sin \theta - {F_{fy}}\cos \theta ) + G} \\ {2{M_f}} \end{array}} \right]$ 为重力和摩擦力矩阵; $B = \dfrac{1}{r}\left[ {\begin{array}{*{20}{c}} {\cos \theta }&{\cos \theta } \\ {\sin \theta }&{\sin \theta } \\ { - \dfrac{L}{2}}&{\dfrac{L}{2}} \end{array}} \right]$ ; $\tau = {\left[ {\begin{array}{*{20}{c}} {{\tau _L}}&{{\tau _R}} \end{array}} \right]^{\rm{T}}}$ ; ${\tau _d}$ 为外部有界扰动.

观察式(7), 机器人的重力和摩擦力矩阵在实际应用中较难测得, 故将其与外界扰动视为系统总扰动. 又 ${S^{\rm{T}}}*{A^{\rm{T}}} = 0$ 故在式(7)两边同时左乘 ${S^{\rm{T}}}(q)$ 以去掉约束力. 同时对式(3)求导可得 $\ddot q = \dot S\eta + S\dot \eta $ , 将其也代入式(7), 则爬壁机器人动力学方程等效为:

$ \bar M\dot \eta + d = \bar B\tau $

(8)

其中, $\bar M = \left[ {\begin{array}{*{20}{c}} m&{} \\ {}&I \end{array}} \right]$ , $\bar B = \dfrac{1}{r}*\left[ {\begin{array}{*{20}{c}} 1&1 \\ { - \dfrac{L}{2}}&{\dfrac{L}{2}} \end{array}} \right]$ , $d = {S^{\rm{T}}}(G + {\tau _d})$ 为系统等效总扰动.

2 轨迹跟踪控制器设计

由上一部分内容可知, 本文中将动力学的重力、摩擦力作用及外部干扰视为系统总扰动, 系统建模存在误差, 故采用改进型非线性干扰观测器对该部分进行前馈补偿.

系统控制器(图3)设计首先对运动学模型采用反演控制算法得出爬壁机器人参考速度和角速度. 其次针对动力学模型设计基于改进型非线性干扰观测器的滑模控制算法, 使系统具有较强的鲁棒性.

2.1 运动学控制器

爬壁机器人在全局坐标系的位姿误差如图4所示, 则机器人在本体坐标系上的位姿误差可定义为:

$ \left[ {\begin{array}{*{20}{c}} {{x_e}} \\ {{y_e}} \\ {{\theta _e}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{e_1}} \\ {{e_2}} \\ {{e_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _d}}&{\sin {\theta _d}}&0 \\ { - \sin {\theta _d}}&{\cos {\theta _d}}&0 \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {X - {X_d}} \\ {Y - {Y_d}} \\ {\theta - {\theta _d}} \end{array}} \right] $

(9)

式中, ${\left[ {\begin{array}{*{20}{c}} X&Y&\theta \end{array}} \right]^{\rm{T}}}$ 为爬壁机器人全局坐标系中的实际位姿, ${\left[ {\begin{array}{*{20}{c}} {{X_d}}&{{Y_d}}&{{\theta _d}} \end{array}} \right]^{\rm{T}}}$ 为参考位姿.

参考文献[13], 得到机器人运动学控制律为:

$ {\eta _r} = \left[ {\begin{array}{*{20}{c}} {{v_r}} \\ {{\omega _r}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{v_d}\cos {\theta _e} + {k_x}{x_e}} \\ {{\omega _d} + {k_y}{v_d}{y_e} + {k_\theta }{v_d}\sin {\theta _e}} \end{array}} \right] $

(10)

其中, $ {v}_{d}$ 、 ${\omega }_{d}$ 为爬壁机器人设定轨迹的理想速度与角速度, $ {k}_{x}$ 、 ${k}_{y}$ 、 ${k}_{\theta }$ 均为正数. 此时定义Lyapunov函数为:

$ {V_1} = \frac{1}{2}{e_1}^2{\rm{ + }}\frac{1}{2}{e_2}^2 + \frac{{1 - \cos ({e_3})}}{{{k_y}}} $

(11)

其中, ${e_3} \in \left[ { - \pi ,\pi } \right]$ , 显然对于任意界限内 ${\left[ {\begin{array}{*{20}{c}} {{e_1}}&{{e_2}}&{{e_3}} \end{array}} \right]^{\rm{T}}} \ne 0$ , 有 ${V_1} > 0$ , ${V_1}$ 正定. 对 ${V_1}$ 求导得:

$ \begin{split} {{\dot V}_1} =& {e_1}{{\dot e}_1}{\rm{ + }}{e_2}{{\dot e}_2} + \frac{{\sin ({e_3}){{\dot e}_3}}}{{{k_y}}} \\ =& - {k_x}{e_1}^2 - \frac{{{v_r}{k_\theta }{{\sin }^2}({e_3})}}{{{k_y}}} \le 0 \\ \end{split} $

(12)

由于 $\sin ({e_3})$ 的存在, 存在 ${e_3} \ne 0$ 时 ${\dot V_1} = 0$ , 故 ${\dot V_1}$ 半负定, 且 ${\dot V_1}$ 不恒等于0, ${\left[ {\begin{array}{*{20}{c}} {{e_1}}&{{e_2}}&{{e_3}} \end{array}} \right]^{\rm{T}}} \to \infty $ 时 ${V_1} \to \infty $ . 故根据Lyapunov定理可得平衡状态是局部渐近稳定的.

2.2 改进型非线性干扰观测器

对于外界干扰, 普通非线性干扰观测器一般将扰动 $d$ 的导数近似成 $\dot d = 0$ , 而实际环境中一般 $\dot d$ 不为0, 故观测效果始终存在误差. 根据机器人系统动力学模型, 参考文献[14,15], 对于系统 $\dot x = f(x) + g(x)u + d$ , 设计改进型非线性干扰观测器如下所示:

$ \left\{ \begin{split} & {{\dot {\textit{z}}}_0} = f(x) + g(x)u + \hat d - {L_0}(x)({{\textit{z}}_0} - x) \\ & \hat d = {{\textit{z}}_1} + {p_1}(x) \\ & {{\dot {\textit{z}}}_1} = - {L_1}(x)(f(x) + g(x)u + \hat d) + {\hat {\dot d}} - ({{\textit{z}}_0} - x) \\ & {\hat {\dot d}} = {{\textit{z}}_2} + x \\ & {{\dot {\textit{z}}}_2} = - (f(x) + g(x)u + \hat d) + v \\ \end{split} \right. $

(13)

其中, $\hat d$ 为实际干扰 $d$ 的估计值; ${\hat {\dot d}}$ 为实际干扰导数 $\dot d$ 的估计值; ${L_i}(i = 0,1)$ 为观测器增益, ${L_1}{\rm{ = }}\dfrac{{\partial {p_1}(x)}}{{\partial x}}$ ; $v$ 为引入的虚拟控制函数.

设计控制律^[16]: $\left\{\!\!\begin{array}{l}s\!=\!\tilde{\dot{d}}\!=\!\ddot{\tilde{x}}\!+\!({L}_{0}+{L}_{1})\dot{\tilde{x}}+({L}_{0}{L}_{1}+1)\tilde{x}\\ v\!=\!-{k}_{1}sat(s)\end{array}\right.$ , $sat(s) = \left\{ {\begin{array}{*{20}{c}} 1,&{s > \Delta } \\ {{s / \Delta }},&{\left| s \right| \le \Delta } \\ { - 1},&{s < - \Delta } \end{array}} \right.$ . 相较于文献[14,15], 该观测器对 ${\dot {\textit{z}}_1}$ 、 ${\hat {\dot d}}$ 、 ${\dot {\textit{z}}_2}$ 的设计进行了改进, 对于 ${\dot {\textit{z}}_1}$ 在等式右边增加“ $ - ({{\textit{z}}_0} - x)$ ”, 修改 ${\hat {\dot d}} = {{\textit{z}}_2} + {L_2}x$ 为 ${\hat {\dot d}} = {{\textit{z}}_2} + x$ 从而设计的控制律更为简单. 该观测器相较于文献[14,15]需设计的参数更少, 并且采用了饱和函数替代符号函数, 削弱抖振.

在实际环境中影响爬壁机器人位姿的原因主要为磁吸附力不足, 并受重力影响从而造成爬壁机器人发生滑移. 故干扰主要为磁吸附力及重力, 其变化一般缓慢, 其 $n$ 阶导满足条件: $\left| {\dfrac{{{d^j}d(t)}}{{d{t^j}}}} \right| \le D,j = 0,1,2,\cdots,n$ , 即干扰及其任一阶导有界.

针对爬壁机器人系统, 取: ${p_i}(x) = - {L_i}(x)\bar M\eta = {L_i}x$ , $x = - \bar M\eta $ , $u = \tau $ , $g(x) = - \bar B$ , 有:

$ \left\{ \begin{split} & {{\dot {\textit{z}}}_0} = - \bar B\tau + \hat d - {L_0}(x)({{\textit{z}}_0} + \bar M\eta ) \\ & \hat d = {{\textit{z}}_1} - {L_1}(x)\bar M\eta \\ & {{\dot {\textit{z}}}_1} = - {L_1}(x)( - \bar B\tau + \hat d) + {\hat {\dot d}} - ({{\textit{z}}_0} + \bar M\eta ) \\ & {\hat {\dot d}} = {{\textit{z}}_2} - \bar M\eta \\ & {{\dot {\textit{z}}}_2} = - ( - \bar B\tau + \hat d) + v \\ \end{split} \right. $

(14)

定义改进型非线性干扰观测器的观测误差为:

$ \left[ {\begin{array}{*{20}{c}} {\tilde x} \\ {\tilde d} \\ {{\tilde {\dot d}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\textit{z}}_0} - x} \\ {\hat d - d} \\ {{\hat {\dot d}} - \dot d} \end{array}} \right] $

(15)

则,

$ \left( {\begin{array}{*{20}{c}} {\dot {\tilde x}} \\ {\dot {\tilde d}} \\ {\dot {\tilde {\dot d}}} \end{array}} \right) = \left\{ {\begin{array}{*{20}{l}} { - {L_0}\tilde x + \tilde d} \\ { - {L_1}\tilde d + {\tilde {\dot d}} - \tilde x} \\ { - \tilde d - \ddot d + v} \end{array}} \right. $

(16)

变换等式得:

$ \left\{ \begin{split} & \tilde d = {\dot {\tilde x}} + {L_0}\tilde x \\ & {\tilde {\dot d}} = {\ddot {\tilde x}} + {L_0}{\dot {\tilde x}} + {L_1}({\dot {\tilde x}} + {L_0}\tilde x) + \tilde x \\ &\;\;= {\ddot {\tilde x}} + ({L_0} + {L_1}){\dot {\tilde x}} + ({L_0}{L_1} + 1)\tilde x \\ \end{split} \right. $

(17)

令Lyapunov函数为:

$ {V_2} = \frac{1}{2}{\tilde x^2} + \frac{1}{2}{\tilde d^2}{\rm{ + }}\frac{1}{2}{{\tilde {\dot d}}^2} $

(18)

显然 ${V_2} \ge 0$ , 有且仅当 $ \tilde{x}$ 、 $\tilde{d}$ 、 $\tilde{\dot{d}}$ 等于零时, ${V_2}{\rm{ = }}0$ , ${V_2}$ 正定. 对 ${V_2}$ 求导得:

$ \begin{split} {{\dot V}_2} &= \tilde x{\dot {\tilde x}} + \tilde d{\dot {\tilde d}}{\rm{ + }}{\tilde {\dot d}}\dot {\tilde {\dot d}} \\ & = \tilde x( - {L_0}\tilde x + \tilde d) + \tilde d( - {L_1}\tilde d + {\tilde {\dot d}} - \tilde x) + {\tilde {\dot d}}( - \tilde d - \ddot d + v) \\ & = - {L_0}{{\tilde x}^2} - {L_1}{{\tilde d}^2} - {\tilde {\dot d}}(\ddot d - v) \\ & \le\ - {L_0}{{\tilde x}^2} - {L_1}{{\tilde d}^2} - \left| {{\tilde {\dot d}}} \right|({k_1} - D) \\ \end{split} $

(19)

为满足Lyapunov定理, 取 ${L_0} > 0$ , ${L_1} > 0$ , ${k_1} \ge D$ , 使得 ${\dot V_2} \le 0$ .

2.3 动力学控制器

通过设置增益将干扰观测器观测到的干扰转化为相应干扰输入控制量, 即:

$ {\tau _{{f}}} = \hat d $

(20)

取干扰输入量的增益为 ${\bar B^{ - 1}}$ , $\tau = {\tau _{BS}} + {\tau _f}$ , 则系统模型可转换为:

$ \begin{split} \dot \eta & = {{\bar M}^{ - 1}}(\bar B\tau - d) \\ &= {{\bar M}^{ - 1}}(\bar B({\tau _{BS}} + {{\bar B}^{ - 1}}{\tau _f}) - d) \\ & = {{\bar M}^{ - 1}}(\bar B{\tau _{BS}} + \tilde d) \\ \end{split} $

(21)

由上式可知, 采用相应干扰观测器后, 系统的干扰减少, 根据转变后的系统设计动力学控制器.

令 ${e_c}(t) = \left[ {\begin{array}{*{20}{c}} {{e_v}} \\ {{e_\omega }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{v_r} - v} \\ {{\omega _r} - \omega } \end{array}} \right] = {\eta _r} - \eta $ , 选择PI滑动面为:

$ s(t) = \left[ {\begin{array}{*{20}{c}} {{s_v}(t)} \\ {{s_\omega }(t)} \end{array}} \right] = {e_c}(t) + \beta \int {{e_c}(t){\rm{d}}t} $

(22)

其中, $\;\beta > 0$ . 对滑动面求导得:

$ \dot s(t) = {\dot e_c}(t) + \beta {e_c}(t) $

(23)

将式(21)代入式(23)得:

$ \dot s(t) = \left( {{{\dot \eta }_c} - {{\bar M}^{ - 1}}(\bar B{\tau _{BS}} + \tilde d)} \right) + \beta {e_c}(t) $

(24)

设计的滑模控制主要包括2个部分: 等效控制和切换控制, 即:

$ \begin{split} {\tau _{BS}}& = {\tau _{eq}} + {\tau _{sw}} \\ & = {{\bar B}^{ - 1}}(\bar M\left( {{{\dot \eta }_c} + \beta {e_c}(t)} \right){{ + }}{{{k}}_2}{{s + }}{{{k}}_3}{sgn} (s)) \\ \end{split} $

(25)

但为了削弱“抖振”现象, 引入变速函数^[17] $vs(S,\varepsilon ) = \left[ {\begin{array}{*{20}{c}} {{\varepsilon _1}\left\| {{e_v}} \right\|{sgn} ({s_v})} \\ {{\varepsilon _2}\left\| {{e_\omega }} \right\|{sgn} ({s_\omega })} \end{array}} \right]$ 代替符号函数 ${sgn} (s)$ .

令Lyapunov函数为:

$ {V_3} = \frac{1}{2}{s^{\rm{T}}}s \ge 0 $

(26)

则有式(27):

$ \begin{split} {{\dot V}_3} &= {s^{\rm{T}}}\dot s = {s^{\rm{T}}}({{\dot \eta }_c}(t) - \dot \eta (t) + \beta {e_c}(t)) = {s^{\rm{T}}}\left\{ - {{\bar M}^{ - 1}}\left\{ \left[ {\bar M({{\dot \eta }_c} + \beta {e_c}(t)) + {k_2}s + {k_3}vs(S,\varepsilon )} \right] + \tilde d \right\}{\rm{ + }} {{\dot \eta }_c}(t) + \beta {e_c}(t) \right\}\\ & = {s^{\rm{T}}}\left\{ \begin{array}{l} - {k_2}{{\bar M}^{ - 1}}s -{k_3}{{\bar M}^{ - 1}}vs(S,\varepsilon ) - \tilde d \end{array} \right\}= - {s^{\rm{T}}}{k_2}{{\bar M}^{ - 1}}s - {k_3}\left| {{s^{\rm{T}}}} \right|{{\bar M}^{ - 1}}\left[ \begin{array}{l} {\varepsilon _1}\left\| {{e_v}} \right\|\\ {\varepsilon _2}\left\| {{e_\omega }} \right\| \end{array} \right] - {s^{\rm{T}}}\tilde d \\ & \le - {s^{\rm{T}}}{k_2}{{\bar M}^{ - 1}}s -\left| {{s^{\rm{T}}}} \right|\left( {{k_3}{{\bar M}^{ - 1}}\left[ \begin{array}{l} {\varepsilon _1}\left\| {{e_v}} \right\|\\ {\varepsilon _2}\left\| {{e_\omega }} \right\| \end{array} \right] - \left| {\tilde d} \right|} \right) \end{split} $

(27)

要使系统稳定则 ${k_2}\!\! \ge \!\!0$ 且 ${k_3}\!\! \ge\!\! \max \left( {\dfrac{{\left| {{{\tilde d}_1}} \right|}}{{m{\varepsilon _1}\left\| {{e_v}} \right\|}}\!,\!\dfrac{{\left| {{{\tilde d}_2}} \right|}}{{I{\varepsilon _2}\left\| {{e_\omega }} \right\|}}} \right)$ , $\left| {\tilde d} \right| = \left[ \begin{gathered} \left| {{{\tilde d}_1}} \right| \\ \left| {{{\tilde d}_2}} \right| \\ \end{gathered} \right]$ , 此时 ${\dot V_3} \le 0$ .

综上所述, 对于整个闭环系统, 考虑Lyapunov函数: $V = {V_1} + {V_2} + {V_3} \ge 0$ ; $\dot V = {\dot V_1} + {\dot V_2} + {\dot V_3} \le 0$ , 根据Lyapunov定律可知整个闭环系统是渐近稳定的.

3 Matlab仿真验证

以履带式机器人为研究对象, 机器人参数为: $m $ =10 kg, $ I$ =5 kg·m², $r $ =0.05 m, $L $ =1 m.

为了验证该控制律的有效性, 本文根据爬壁机器人一般在壁面上的爬行路径, 设计了“S”形路径, 公式如式(28)所示.

$\! \begin{gathered} x = \left\{ {\begin{array}{*{20}{l}} {0.25t},&{0 \le t < 30} \\ {7.5 + 2.5\sin\left( {0.1t - 3} \right)},&{30 \le t \le 30 + 10\pi} \\ {7.5 - 0.25\left( {t - 30 - 10\pi} \right)},&{30 + 10\pi < t < 50 + 10\pi} \\ {2.5 + 2.5\sin\left( {0.1t - 5} \right)},&{50 + 10\pi \le t \le 50 + 20\pi} \\ {2.5 + 0.25\left( {t - 50 - 20\pi} \right)},&{50 + 20\pi < t < 70 + 20\pi} \\ {7.5 + 2.5\sin\left( {0.1t - 7} \right)},&{70 + 20\pi \le t < 70 + 30\pi} \\ {7.5 - 0.25\left( {t - 70 - 30\pi} \right)},&{70 + 30\pi < t < 90 + 30\pi} \\ {2.5 + 2.5\sin\left( {0.1t - 9} \right)},&{90 + 30\pi \le t \le 90 + 40\pi} \end{array}} \right. \!, y = \left\{ {\begin{array}{*{20}{l}} 1,&{0 \le t < 30} \\ {{{3.5 - 2.5\cos(0.1t - 3)}}},&{30 \le t \le 30 + 10\pi} \\ 6,&{30 + 10\pi < t < 50 + 10\pi} \\ {{{8.5 + 2.5\cos(0.1t - 5)}}},&{50 + 10\pi \le t \le 50 + 20\pi} \\ {11},&{50 + 20\pi < t < 70 + 20\pi} \\ {{{13.5 - 2.5\cos(0.1t - 7)}}},&{70 + 20\pi \le t < 70 + 30\pi} \\ {16},&{70 + 30\pi < t < 90 + 30\pi} \\ {{{18.5 + 2.5\cos(0.1t - 9)}}},&{90 + 30\pi \le t \le 90 + 40\pi} \end{array}} \right. \\ \end{gathered} $

(28)

该路径包括匀速直线运动, 顺时针匀速圆周运动及逆时针匀速圆周运动, 初始姿态为 ${\left[ {\begin{array}{*{20}{c}} 0&0&0 \end{array}} \right]^{\rm{T}}}$ . 假设外界干扰为 $d = 5{\sin ^3}(t) + {e^{ - t}} - \cos (t)$ , 控制参数设计为: ${k_x} = 0.1$ , ${k_y} = 3$ , ${k_\theta } = 1$ , ${L_0} = 1$ , ${L_1} = 10$ , ${\varepsilon _1} = {\varepsilon _2} = 1$ , $\;\beta = 5$ , $\Delta = 5$ , ${k_1} = 85$ , ${k_2} = 50$ , ${k_3} = 1$ . 仿真结果如图5所示.

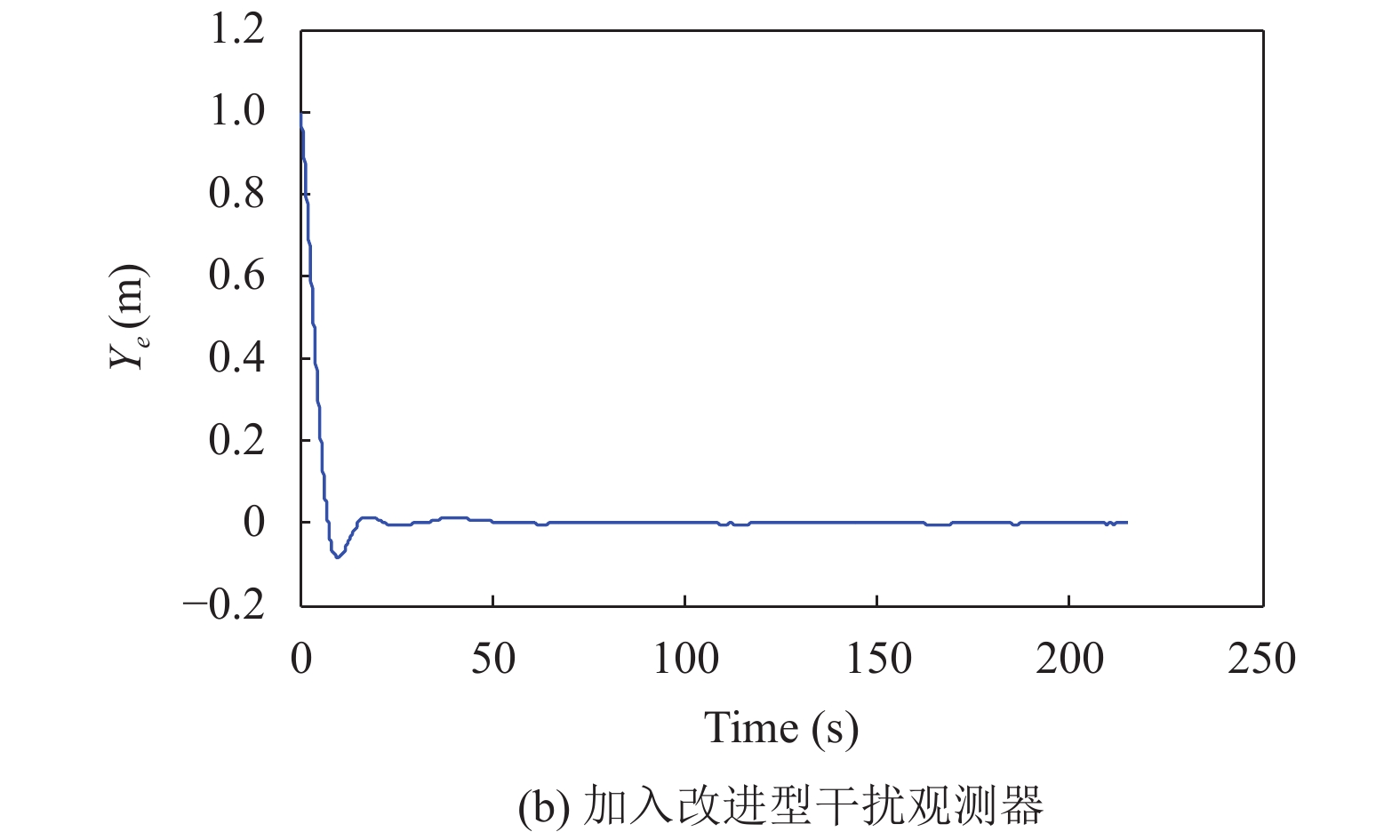
由图5–图7所示, 可以观察到虽然常规滑模控制也可以得到比较好的跟踪效果, 但常规滑模控制的误差存在抖振, 位置误差为5 cm左右, 姿态角误差也在 $ - 0.05^\circ \sim 0.05^\circ $ 内振荡. 相较而言, 加入改进型干扰观测器后的控制律位姿误差趋近于0, 鲁棒性能更优, 抗干扰效果也更好, 跟踪效果如图8所示.

而由图9及图10可知, 改进型干扰观测器基本可以拟合外界干扰, 且与文献[14]的干扰观测器相比误差的振荡范围更小, 观测效果更佳.

4 结论

本文为了解决存在建模误差和扰动未知的爬壁机器人轨迹跟踪问题设计控制器, 首先建立了爬壁机器人的运动学及动力学模型, 其次引入干扰观测器对系统建模误差及外部干扰进行观测, 设计出一种基于改进型干扰观测器的反演滑模控制方法. Lyapunov函数证明了系统的稳定性, 仿真结果表明了控制方案的有效性.