1 引言

随着我国的城市化、工业化的高速发展, 我国产生的污水量也随之增加, 对我国的水环境治理造成了巨大的压力, 因此, 在我国水环境治理的新阶段中, 污水处理是保证我国水资源可持续利用与发展的重要部分^[1]. 至2017年底, 我国共建成5000多座城市污水处理厂^[2]. 在污水处理设施覆盖率不断增长的背景下, 污水处理后的水质不达标与成本高等等问题日益明显, 高成本导致部分污水处理厂出现了“养不起”的难题^[3], 因此对污水工艺流程进行优化, 降低污水处理成本迫在眉睫.

与此同时, 城市污水处理过程包括多种水质变量和操作变量, 需要同时满足出水达标排放与高安全性等条件, 因此对污水工艺流程进行优化目标是在保证出水水质的前提下, 降低整体污水处理的工艺成本^[4], 也就是在满足过程约束、处理指标与设定值的条件下, 设计出排放水质符合要求且运行成本最低的解决方案. 但污水处理工艺过程具有指标多、污水成分复杂、考虑因素复杂等特点, 如何在水质达标、成本最低的条件下寻找到最优的处理过程从而实现提质增效, 是如今亟需解决的问题^[5].

为了实现污水处理工艺方案的最优化, 很多学者对此进行了广泛的研究. 刘载文等^[6]给出污水处理过程中多变量最优控制的数学模型, 采用遗传算法求解污水处理过程的优化控制问题, 解决了采用传统算法处理的局部最优问题; 卢薇等^[7]提出一种动态惯性权重的多目标粒子群优化算法, 获得了最优的溶解氧和硝态氮的优化设定值; 赵小强等^[8]利用改进多目标布谷鸟算法同时对污水处理的能耗与出水水质模型进行优化, 并通过利用PID控制器实现对优化设定值的跟踪控制, 使得能够在保证水质的前提下降低了能耗; 赵杨等^[9]采用多策略融合变异和排序优选方法, 将自适应更新交叉率与PID控制器相结合, 实现对溶解氧和硝态氮浓度设定值的动态寻优和跟踪控制. 上述的研究工作均取得了不错的效果.

然而, 以上寻优策略均是在污水处理工艺技术流程长度固定的情况下对环保设备工艺流程进行优化排序或具体设定工艺参数值, 并没有考虑到工艺序列长度可变的性质, 缺少了调度的灵活性, 难以用于全流程优化运行.

针对以上问题, 本文首先建立了污水处理工艺知识库. 其次, 在建立工艺知识库的基础上, 采用messy遗传算法对工艺流程进行寻优, 并根据污水处理的指标要求对算法的适应度函数以及选择策略进行了改进, 给出了基因长度不定的种群所特有的进化方式, 以实现不定长污水处理工艺流程的优化. 最后, 通过实验验证, messy遗传算法能够在工艺序列长度变化的情况下实现方案的高效准确的推荐.

2 污水处理工艺知识库

污水处理工艺知识库的建立是工艺优化系统实现的基础, 污水处理工艺流程的经济技术指标一般包含下列内容: 处理单位水量投资、缩减单位污染物投资、处理单位水量电耗和成本、缩减单位污染物电耗和成本、占地面积、运行性能可靠性、管理维护难易程度、总体环境效益等. 另外, 每一种处理技术都应该提供设计参数、处理成本计算公式以及处理效率或处理量计算公式, 以便进行正向或反向的计算.

单一的处理方式往往无法将含有多种污染物的污水彻底处理到污染物的期望指标以下, 需要根据给定的原污水水质, 水量, 期望处理程度, 成本上限等来将多个处理模块组装起来, 以保证通过该组合后的工程处理后的污水在给定的指标范围之内.

和一般的调度问题不同, 污水处理工程并不要求每一步的污水处理模块不同, 而工程本身也不限制其长度. 这就意味着遗传算法必须针对多个基因长度不同的种群进行并行计算, 并且还要将每个种群中最优的个体进行汇总比较, 以生成最优的工程安排. 但每一步的可重复性使得遗传算法中基因本身的变化方式变得简单, 每个种群内部个体的基因中的每一小段均对应多种工艺库里的模块以及对应的处理效率, 其中处理效率随机指定, 或者通过工程师的设计历史挑选. 本文中提到的污水处理工艺优化系统设计了技术的使用记录, 当工程师用户通过本系统进行工艺流程安排时, 所使用过的模块以及对应效率会被作为工艺历史记录以供参考.

整个知识库由多个工艺库和工艺历史记录组成, 每个工艺库中包含多个工艺处理模块. 在本文中, 整个污水处理过程分为3个单元: 预处理单元、生物处理单元、尾处理单元.

其具体含义为:

(1)预处理单元由格栅、沉砂池、沉淀池组成;

(2)生物处理单元包含多个步骤的工艺处理模块, 这些模块来自于多个工艺库和工艺历史. 生物处理单元中还包括深度处理单元, 用来处理经过工艺流程处理后的污水; 与前文一致, 此处的工艺处理效率特指处理后污染物质的占有百分比)

(3)尾处理单元包括沉砂池、沉淀池.

参考城市污水处理工艺的设计^[10], 给出概念图如图1所示.

该污水处理知识库的数据主要来源于以下方面: (1)本文中提到的污水处理工艺优化系统的技术使用记录; (2)对各类公开标准及成熟污水方案中的工艺模块数据的收集. 其所收集的数据主要包含以下指标: 工艺基本信息(包含工艺名称、工艺内容等), 处理单位水量成本及其计算方式, 缩减单位污染物成本及其计算方式等信息.

如何设定生物处理单元中工艺技术的先后顺序和长度, 以及各工艺技术的处理效率, 以最少的成本使污水的各项指标达标, 是本文所要解决的问题.

3 Messy遗传算法的应用与改进

针对污水处理应用场景下, 工艺技术流程的调度问题以及其长度可变的性质, 本文采用了messy遗传算法. 本节对污水处理工艺流程问题进行定义, 并且介绍messy遗传算法在本场景的设计、改进与应用.

3.1 污水处理工艺流程问题的数学描述

一般来讲, 污水中的污染物不仅包含一种, 而本文将讨论如何以数学形式对问题进行定位并解决, 分析给定多种污染物的初始量和处理指标的条件下如何使用算法进行处理流程的优化.

令生物处理单元中的工艺总体流程为集合 ${\cal{A}}$ , 工艺知识库

$ {\cal E} = \left\{ {{{\cal T}_1},{{\cal T}_2}, \cdots ,{{\cal T}_n},{\cal H}} \right\} $

(1)

其中, ${{\cal T}_i}$ 为工艺库, ${\cal H}$ 为工艺历史记录, 每个工艺库和工艺历史记录的元素表示如下:

$ {{\cal T}_i} = \left\{ {{t_1},{t_2}, \cdots ,{t_m}} \right\} $

(2)

$ {\cal H} = \left\{ {{h_1},{h_2},\cdots,{h_k}} \right\} $

(3)

${t_i}$ 和 ${h_i}$ 均表示具体的工艺技术模块, 而每个 ${t_i}$ 和 ${h_i}$ 均可表示如下:

$ r = \left( {{e_1},{e_2}, \cdots ,{e_v}} \right) $

(4)

$ {t_i} = \left( {r,p\left( r \right),c\left( r \right)} \right) $

(5)

$ {h_i} = \left( {r,p\left( r \right),c\left( r \right)} \right) $

(6)

其中,r为该工艺技术处理污水的效率, ${e_i}$ 表示该技术处理污水中某种物质的效率, $p\left( r \right)$ 为工艺参数, $c\left( r \right)$ 为处理成本, $p\left( r \right)$ 和 $c\left( r \right)$ 因不同处理工艺而异, 其作用是能够将指定的处理效率作为输入, 反推出该工艺技术模块的设定参数和预计成本.

所以本文主要研究的问题是: 如何根据给定的待处理污染物含量 ${l_{\rm start}} = \left( {{l_1},{l_2}, \cdots ,{l_v}} \right)$ 以及指标要求 ${l_{\rm require}} = \left( {{l_1},{l_2}, \cdots ,{l_v}} \right)$ , 通过工艺知识库 ${\cal E}$ 给定的数据, 计算出低成本高效的处理流程 ${\cal A}$ , 其中工艺模块可重复数量(即 ${\cal A}$ 中元素可重复的个数)为b, 初始工艺长度(即 ${\cal A}$ 中元素的总个数)为 ${n_{\rm init}}$ :

$ {\cal A} = \{ {g_1},{g_2}, \cdots ,{g_v}|{g_i} \in {{\cal T}_1} \cup {{\cal T}_2} \cup \cdots \cup {{\cal T}_n} \cup {\cal H}\} $

(7)

其中, 处理流程 ${\cal A}$ 满足:

$ {l_{\rm end}} = {l_{\rm start}}\mathop \prod \nolimits_{i = 1}^{m \times n + k} \left( {1 - {r_i}} \right),\;\;{l_{\rm end}} < {l_{\rm require}} $

(8)

每一个工艺模块 ${g_i}$ 与每一步的处理效率 ${r_i}$ 相对应, 因此 $1 - {r_i}$ 表示经过工艺模块 ${g_i}$ 处理后污水内对应污染物的剩余百分比, 如果相乘的结果小于规定的指标或者剩余百分比则处理流程 ${\cal A}$ 为满足条件的工艺序列.

另外, 工艺序列的优化目标为:

$ \min \mathop \sum \nolimits_{i = 1}^{m \times n + k} {c_i}\left( r \right) $

(9)

每一个工艺模块 ${g_i}$ 与每一步的成本计算公式(或成本值) ${c_i}$ 相对应, 每一步的成本总和即处理流程 ${\cal A}$ 的总成本, 对于本文所提出的污水工艺优化问题而言, 最主要的优化目标是处理流程总成本的最小化.

3.2 遗传算法的设计

遗传算法是一种解决最优化问题的方法, 其模拟了自然界物种的遗传、交叉和变异的现象. 遗传算法的每个个体可以视为最优化问题的一个解, 并根据待求解问题的目标函数对每个个体进行评估, 给出每个个体的适应度. 当遗传算法开始迭代时, 最初会随机产生一定数量的个体, 并进行遗传、交叉和变异产生新个体, 再根据个体适应度, 保留适应度高的个体, 淘汰适应度低的个体, 因此新个体遗传了上一代的优良性状, 使得算法向问题更优解的方向进行进化, 最终求出最优解. 由于遗传算法能够解决全局最优化问题, 对污水工艺优化问题进行求解, 也不需要复杂计算, 且messy遗传算法能够适应污水处理工艺序列长度变化的情况, 因此本文使用messy遗传算法对污水处理工艺流程进行优化.

由于污水处理领域内的计算机智能流程方案优化推荐案例较少, 本文仅以有限的计算机知识与对环保领域的了解, 针对问题进行了遗传算法的初步设计:

编码: 在本文中采用了基于工序的表示方法, 该方法将工艺知识库的工艺技术编码为序列, 并根据它们在染色体中出现的顺序加以解释.

初始群体选取: 初始群体是从随机生成的一定数目的个体中选择最优个体组成的. 选取最优个体的过程迭代, 直到初始群体中个体数达到了预先确定的规模. 对于本文所研究的问题, 个体的工艺技术顺序不受限制, 并且每个工艺技术从工艺库中进行挑选.

总体衍变策略: 采取了交叉和变异概率随迭代周期发生变化的自适应性遗传算法, 个体选择概率按照基于排序的适应度分配, 为保证迭代周期中适应度的稳步上升, 采用锦标赛选择法.

由于污水处理工艺编排是长度不固定的, 因此使用了messy遗传算法, 但由于messy遗传算法并非传统的种群基因定长的遗传算法, 所以其对应的交叉策略以切断算子和拼接算子来代替, 切断算子与拼接算子的定义在下一部分会详细讲解. 由于种群内每个个体的基因长度不尽相同, 为了保证变异的均匀性, 对于每次发生变异的个体, 其变异位的数量取决于基因长度乘以固定的比例.

以该初步设计为基础, 本文在下一部分会根据污水处理的指标要求对算法的适应度函数以及选择策略进行进一步的修改.

3.3 确定进化策略

对于遗传算法, 其选择、交叉、变异的概率设定和具体函数方法将直接影响算法在最优解方向上的收敛性. 采用自适应遗传算法的思想, 群体在不同的适应度分布情况下交叉和变异的概率会随之变化: 当群体中每个个体的适应度收敛于少数几个值时交叉和变异概率会增加, 反之若个体的适应度分布比较分散时, 交叉和变异概率会减少.

Messy遗传算法考虑到种群基因长度变化的特性, 以切断算子和拼接算子代替了原本的交叉操作, 从而保证了进化过程中基因长度的调整, 使个体的适应度值趋近于最优的同时其它指标也贴近问题的要求, 即能够解决污水处理工艺流程中水质达标、成本最低且不过度处理污染物的要求. 由于工艺模块之间无严格的顺序描述, 在种群中的个体经过拼接操作和变异操作后, 会对每个个体所对应基因的基因座按照工艺模块在知识库中的id进行升序排序, 以便操作和观察. 而本节主要讲述messy遗传算法的详细设计.

适应度函数的重新设计: 在实际的应用当中, 工艺模块成本一般来讲是比较大的数. 本次实验所采用的数据当中, 每个工艺模块的成本的取值区间为[1000,5000], 因此取得倒数后的值将会处于极小的区间范围之内, 此时的适应度对比优势不明显, 从而使个体适应度差异变小, 继续优化的潜能降低, 可能获得某个局部最优解.

为了防止种群进化过程中的局部收敛, 本文对适应度函数进行了重新设计:

$ fitness\left( I \right) = \frac{{one\_module\_cost \times {n_{init}}}}{{total\_cost}} $

(10)

其中, $one\_module\_cost$ 表示单个模组的成本, 一般取候选工艺库中所有工艺模块的平均成本或最大成本, ${n_{\rm init}}$ 表示算法运行初期种群内所有个体基因长度(工艺序列长度)的初始值, $total\_cost$ 为当前个体的基因所对应的工艺序列的总成本. 将成本值取倒数之后, 根据实际工艺候选项情况与初始基因长度, 使其乘以一个合适的常数, 作为个体的适应度. 与原来的适应度函数相比, 新的适应度函数放大了适应度的变化区间, 使个体适应度的对比更加明显, 有效缓解算法过早收敛和局部收敛的问题.

选择: 首先, 根据污水处理优化问题的要求, 对种群内的所有个体进行是否能够满足污水处理要求的判断, 将工艺流程不能将污水处理达标所代表的个体从种群中去除. 其次, 判断种群中是否仍有满足条件的个体: 如果没有满足条件的个体, 则算法结束, 无法根据给定的条件找出严格符合的个体, 即所有个体所表的工艺流程无法将污水处理达标; 如果有满足条件的个体, 则将种群内的空缺位置以符合条件的个体进行随机填补, 直到种群内个体的数量达到预设的种群规模.

对于经过第一步条件筛选后的种群, 使用锦标赛选择策略选择适应度较高的个体进入下一代. 该策略保证了种群的收敛性, 使较高适应度的个体能够稳定遗传至下一代.

经过两步选择, 种群在符合给定条件的情况下, 能够往高适应度方向进化.

切断算子与拼接算子: 由于messy遗传算法的特殊性, 以切断算子和拼接算子代替原有的交叉操作.

切断算子: 以预设的概率在个体所对应的基因中随机挑选一个位置, 在此处将基因一分为二, 形成两个新的个体. 在此过程中种群的规模将会扩大.

拼接算子: 以预设的概率挑选两个个体, 将两个个体的基因组合, 形成一个个体的基因型. 在经过切断算子过程的种群中进行若干轮随机筛选, 每次随机两个个体进行拼接, 形成的个体加入到新的种群, 直至种群规模达到预设规模. 其中, 两个个体之间可能有重复的基因座(工艺模块), 根据预设的工艺模块可重复值b, 若拼接后该工艺模块的重复数量大于b, 则不将该重复模块加入新个体.

变异: 在messy算法中, 基因的长度是不断变化的, 为了保证变异的均匀性, 每次的变异按照预设的变异比例使基因中的若干个基因座进行变异, 若变异后的基因座与原基因中的其他基因座有重复项, 则根据预设的可重复值b, 若变异后该基因座的重复数量大于b, 则去除该基因座.

概率设定: 切断算子与拼接算子取代了原有的交叉操作, 所以两个操作的触发概率均设定如下, 使用余弦函数, 对概率曲线进行处理^[11]:

$ {P_c} = 0.4 \times \cos \left( {\frac{T}{K} \times \frac{\pi }{2}} \right) + 0.2 $

(11)

其中, T是当前进化代数, K是总进化代数. 切断和拼接的概率随着遗传代数的增长逐渐减小, 目的是进化前期注重交叉运算, 全局搜索能力强.

类似于上述公式, 变异概率设定如下:

$ {P_m} = 0.045 \times \sin \left( {\frac{T}{K}\times \frac{\pi }{2}} \right) + 0.005 $

(12)

其中, T是当前进化代数, K是总进化代数. 变异概率随着遗传代数的增长逐渐增加, 目的是进化后期注重变异运算, 局部搜索能力强.

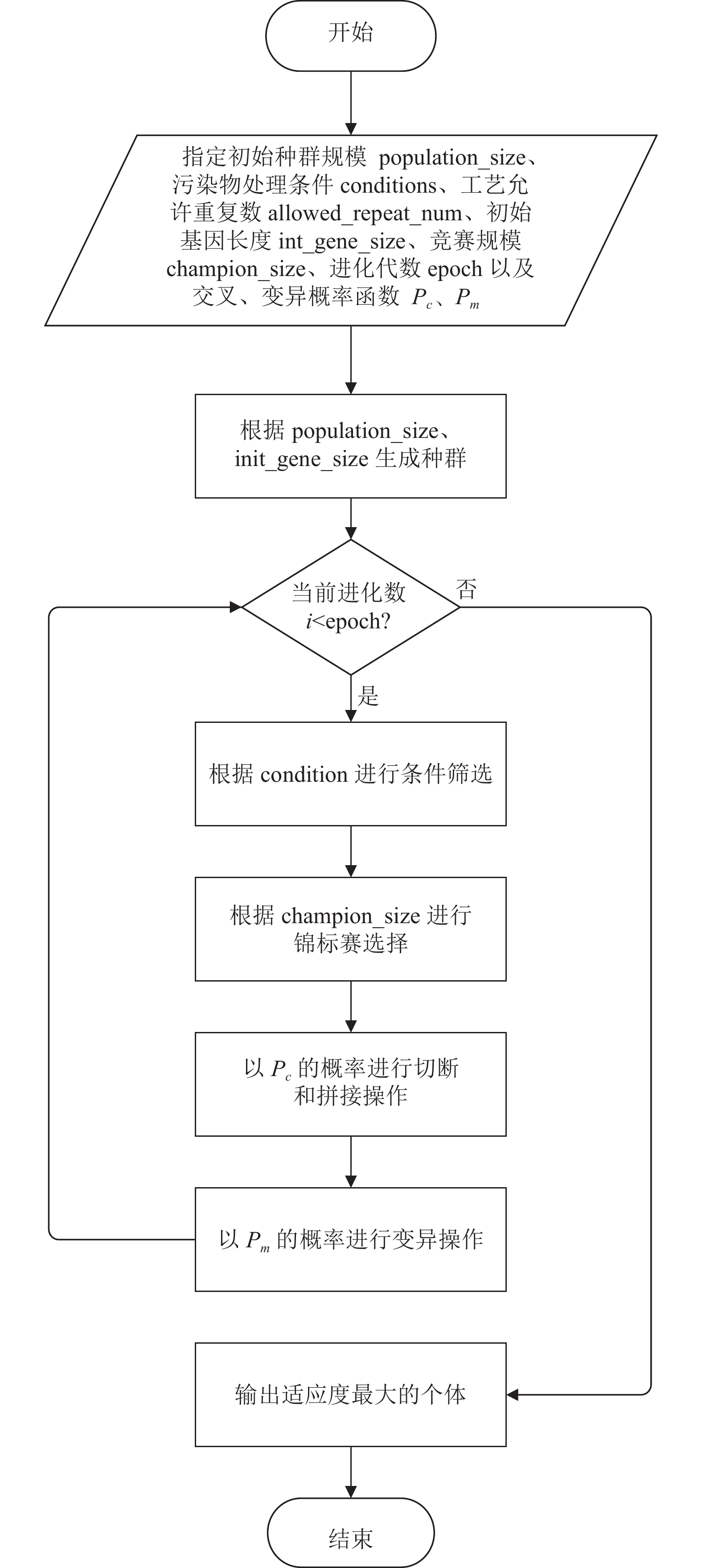
为使messy算法的进化策略清晰易懂, 下面给出该算法的流程图, 如图2所示.

4 实验

以包含14个工艺模块的工艺库, 需要处理3种污染物的优化问题为例, 以上述的遗传算法对污水处理工艺流程优化问题进行求解. 实验硬件环境为处理器为Intel(R) Core(TM) i7-7700 CPU @ 3.60 GHz, GPU为GeForce GTX 1080 Ti, 内存为8 GB 的服务器, 软件环境为Python 3.6.0, Pandas 1.2.4, Numpy 1.20.2. 用于候选工艺模块的工艺库数据如表1, 为系统随机生成, 用于测试.

表1中工艺技术共有14种, 污染物有3种, 工艺初始长度为7.

实验的初始要求: 给定上述数据, 对污水处理工艺进行优化推荐, 所推荐的工艺序列能够使处理后的污水满足给定的污染物百分比含量指标, 每种指标的百分比含量要求分别为0.6, 0.9, 0.6以下, 且该工艺序列为成本最低的序列. 另外, 工艺模块的允许重复数量为1(即没有重复的工艺模块).

本文在messy遗传算法的概率设定方面做了对比实验, 包括固定变异和交叉概率的条件下以及变异和交叉概率随进化代数变化的情况下算法的进化过程. 并且实验对每一轮进化所产生的最大适应度个体相对于给定条件所产生的条件误差进行了测量, 条件误差的大小反映了工艺序列是否“刚好满足条件”, 如果误差过大则说明该工艺序列“用力过度”, 处理的污染物比指标要求多很多, 以下是对条件误差的定义:

$ condition\_error = \frac{{\displaystyle\mathop \sum \nolimits_{i = 1}^v \left( {{l_{{\rm{require}}\;i}} - {l_{{\rm{individual}}\;i}}} \right)}}{{count\left( {{l_{\rm require}}} \right)}} $

(13)

其中, ${l_{{\rm{require}}\;i}}$ 表示第i项的指标要求, ${l_{{\rm{individual}}\;i}}$ 表示个体在第i项的指标下的实际值. 将每一项的指标要求与个体的每一项指标下的实际值作差, 并且将所有差值相加后按指标数量求平均值, 最终所得结果即为条件误差. 条件误差反映了工艺序列的拟合程度.

在两种情况下的实验中, 所取工艺库和进化策略相同, 除了变异和交叉概率不同, 并且进化代数均设为500代, 初始种群规模为200, 每次选择竞赛的规模为3, 工艺模块的允许重复数量为1 (即没有重复的工艺模块).

首先是在固定变异或交叉概率的条件下, messy遗传算法的实验结果, 在本次实验中固定变异和交叉概率分别取值为0.6和0.05, 在固定变异或交叉概率的条件下最大适应度随进化代数的变化趋势如图3(a)所示, 在固定变异或交叉概率的条件下条件误差随进化代数的变化趋势如图3(b)所示.

其次是变异或交叉概率随进化代数变化的条件下的实验结果, 在变异或交叉概率随进化代数变化的条件下最大适应度随进化代数的变化趋势如图3(c)所示, 在变异或交叉概率随进化代数变化的条件下条件误差随进化代数的变化趋势如图3(d)所示.

图3中最大适应度表示当前迭代下种群个体的最大适应度, 适应度越大表示当前种群最优个体对问题的解更优, 其详细定义叙述在第3.2节. 条件误差表示了工艺序列的拟合程度, 即当前最优个体的工艺编排刚好满足污染物处理要求的程度, 越低表示越能够刚好污染物处理满足要求.

由图3(a)和图3(c)可以看出, 变异和交叉概率固定与变异和交叉概率不固定两种情况下messy算法均取得了最优解. 从图3(b)和图3(d)可以看出, 两种条件下条件误差最终保持在0.08到0.1之间, 说明拟合的效果较好. 并且在变异或交叉概率随进化代数变化的情况下, messy算法不会发生过早的收敛, 能够及时跳出局部最优解.

5 结束语

在此工作中, 我们通过将工艺流程调度优化问题进行数学化分析, 从而确定并设计了messy遗传算法的进化策略, 将messy遗传算法应用于污水处理工艺流程调度优化问题. 通过实验验证messy遗传算法在污水处理工艺流程调度优化问题是可行且有效的. 在实际生产应用中, 可通过使用messy遗传算法对污水处理工艺流程调度进行寻优, 设计出能够满足污水处理能力的情况下成本最低的污水工艺流程优化方案, 对污水处理厂实现提质增效具有重要意义.