大数据时代下, 互联网为我们提供方便的同时, 也给我们带来了困扰, 网络中的信息呈爆炸式增长, 从海量的信息中挖掘出对我们需要的信息非常重要^[1]. 随着网络上电影数量的增加, 用户不得不花费大量精力来挑选自己感兴趣的电影. 此时, 个性化推荐系统的出现在一定程度上解决了信息过载问题^[2], 它可以通过分析用户的历史行为特征和有关的数据信息, 为用户推荐可能感兴趣的项目, 起到了信息筛选的作用.

现有的个性化电影推荐算法主要有协同过滤算法、基于内容的推荐算法和混合推荐算法等, 其中, 传统的协同过滤算法(collaborative filtering)应用最为广泛^[3]. 它具有算法复杂性较低、对原始数据的数据内容要求较低的优势. 该算法通过分析用户对于电影的历史评分, 进而找到相似用户, 并根据相似用户的电影评价记录为目标用户推荐电影.

但是协同过滤算法在实际应用中也存在很多缺陷, 比如冷启动、数据稀疏性问题. 基于此, 国内外学者做了大量实验研究. Lokhande等^[4]提出了一种融合层次聚类和主成分分析的混合推荐算法模型, 降低了用户-评分矩阵的稀疏性, 提高了传统协同过滤算法的推荐精度. 杨秀梅等^[5]根据已有用户对不同新闻的浏览历史记录提取其上下文信息, 解决了新闻推荐系统中的新用户冷启动问题, 提高了用户满意度. 但是以上研究基本上是依据用户的评分数据进行分析的, 并没有考虑用户间的信任度关系, 对于电影推荐系统中的用户来说, 其信任朋友的推荐的影片可能会更值得信赖, 推荐效果更能使用户感兴趣. 基于此, 俞美华^[6]提出一种融合用户兴趣度的电影推荐算法, 通过改进用户相似度的计算方法, 提供个性化推荐. Sasmita等^[7]提出了用户相似性和加权信任传播相结合的信任矩阵度量方法, 通过使用反向传播、深度神经网络来进行电影推荐. 但是上述算法没有充分挖掘用户之间的隐式信任关系, 没有建立相对完整的信任机制, 会出现信任关系不完整的问题.

另一方面, 目前电影推荐算法大多数都是基于用户之间的相似度或者物品之间的相似度, 主要关注推荐的准确率, 推荐热门物品给用户, 而忽略了非热门物品的推荐机会, 从整体推荐结果上来看, 推荐种类多样性较低、用户容易产生审美疲劳. 针对用户的个性化需求, 为用户推荐他们感兴趣但难以发现的商品, 即将长尾商品准确地推荐给需要它的用户是个亟待解决的问题^[8-10]. Zhou等^[11]使用传导的方法将热门项目的权重传递给长尾项目, 提高长尾项目的推荐度, 提高了系统的推荐多样性, 但是系统准确率较低. Adamopoulos等^[12]针对物品的概率分布计算相似度, 提高了系统的多样性和准确度, 但是作者只分析了显性评分. 因此, 在保证准确率的前提下提升推荐算法的多样性具有一定的研究意义.

综上所述, 本文对传统的协同过滤算法进行改进, 针对于推荐准确性和多样性, 提出了一种融合信任因子的多样化电影推荐算法. 本算法首先挖掘用户的属性特征和用户之间的信任度关系, 将其和传统的相似度计算方法结合, 保证了每位用户推荐的可靠度和可信度. 然后使用改进类簇中心确认方法的K-means聚类方法, 将拥有相同兴趣爱好的用户聚集在同一个社群中. 最后在用户推荐阶段使用重排序方法, 通过加入惩罚因子来计算电影推荐度, 提高了电影推荐算法的整体多样性, 同时能够在一定程度上解决冷启动和数据稀疏性问题

1 融合信任因子的相似度算法

信任关系是指用户对于邻居用户的推荐可靠性的认可程度, 认可度越高, 推荐越符合用户兴趣^[13]. 而信任关系受到诸多因素的影响, 比如用户自身属性、社会信任度关系等, 这些因素通常被统称为信任因子^[14]. 本文将信任因子与传统相似度计算方法相融合, 旨在充分挖掘用户信息特征.

1.1 社会信任度关系 1.1.1 传统直接信任度模型

传统的信任关系模型大多数是通过简单计算用户间的交互次数来建立的^{[15, 16]}. 文献[17]提出了一种计算用户直接信任度的方法, 通过最初信任度与用户间成功交互次数的乘积计算得到用户直接信任度, 如式(1)所示. 其中Init(u, v)为初始信任度, 计算方法如式(2)所示, ${I_{{u}}} \cap {I_v}\;$ 为用户u和用户v交互的次数, d为设置的阈值, 表示两个用户成功建立信任关系最少的交互次数, 文献实验证明, d取值为80效果最佳. ${{cou}}n{t_t}\;$ 表示两用户交互的总次数, ${{c}}oun{t_s}\;$ 表示用户交互成功的次数, 此处交互成功的标准为两用户对于同一项目的评分小于2分.

$T(u, v) = Init(u, v)\frac{{coun{t_s}}}{{coun{t_t}}}\;$

(1)

$I{{ni}}t(u, v) = \frac{{\min ({I_u} \cap {I_v}, d)}}{d}$

(2)

1.1.2 改进的直接信任度模型

传统的信任关系模型能够有效地表示用户的信任关系, 但是式(1)中成功交互的计算方法忽略了用户之间对于非感兴趣电影的信任度. 如果两个用户对于某部电影的评分都为1.5分, 根据传统信任度计算方法, 由于两个用户都看过同一电影并且对于电影的评分相同, 系统会认定两用户间有较高的相似度. 但是这个分数只能够说明两个用户对于这部电影不喜爱, 并不能代表用户间喜爱的项目相似. 因此, 针对此问题, 本文在传统信任度模型中引入感兴趣因子, 定义如下:

$I{{n}}terestT(u, v){{ = }}\frac{{{{|}}{{{I}}_{uv}}{{ > D|}}}}{{{{c}}oun{t_t}}}\;$

(3)

其中, $|{I_{{u}}}_v > D|\;$ 表示用户u和用户v共同评分的电影分数大于D的数量, ${{cou}}n{t_t}\;$ 表示两个用户交互的总次数. 如果用户u和用户v对于同一部电影的评分都大于阈值D, 则说明两用户的兴趣比较相似. 基于电影的评分分值区间为1–5, 因此设定阈值D为3.5.

综合得到用户直接信任度模型, 定义如下:

$Trus{t_1}(u, v) = T(u, v) \times InterestT(u, v)$

(4)

1.1.3 间接信任度模型

由于用户-评分矩阵本身比较稀疏, 可能会出现用户u和用户v没有直接信任关系, 但是他们有共同朋友k, 根据信任关系的传递性特征, 用户能够信任自己的直接朋友, 也会在一定程度上信任朋友的朋友. 故本文引入间接信任度, 用ITrust(u, v)表示. 但是随着信任链的长度增加, 信任度会逐渐减弱. 在保证时间复杂度和保留有效用户的前提下, 根据文献[18]对于间接信任的关系研究, 本文只考虑目标用户的两级信任关系.

假设用户v是用户u的二级信任用户, 两用户之间至少存在一条路径, 每条路径表示为 $Path({u_i}, {v_i}) = $ $ (\;{u_i}, k, {v_i})$ , 每条路径的信任度计算方法如下:

$IT{{r}}us{t_i}({u_i}, {v_i}) = Trus{t_1}({u_i}, k) \times Trus{t_1}(k, {v_i})$

(5)

用户的间接信任模型通过计算路径信任度的均值得到, 如式(6), 其中n表示从用户u到用户v的路径数目之和.

$IT{{ru}}st(u, v) = \frac{{\displaystyle\sum\limits_{i \in n} {ITrus{t_i}({u_i}, {v_i})} }}{n}$

(6)

得到用户间接信任度矩阵后, 将其填充到直接信任度矩阵 $Trust_1$ 中, 构建社会信任度关系矩阵Trust(u, v).

1.2 用户属性信息

充分挖掘用户的属性信息是获得用户特征的重要方法, 通过数据挖掘, 我们可以对用户进行更全面而深入的了解, 从而能够更加准确地预测、并推荐适合的电影给用户. 较早尝试将属性信息与推荐算法融合的典型代表有Kazienko等^[19]开发的电商推荐系统, 他通过挖掘用户注册的信息进行推荐, 对于新用户来说, 利用属性特征的推荐算法的点击率达到了89%, 相比于随机推荐提高了62%. 属性信息从某种程度上反映了用户的喜好度, 因此本文对用户的年龄、性别、职业信息进行挖掘.

本文参考文献[20]中的计算方法, 对于用户年龄, 将其划分为7个年龄段, 分别用数值1–7表示(年龄段为: 小于18、18~24、25~34、35~44、45~49、50~55、大于56). 对于用户性别, 用1表示男(M), 0表示女(F). 对于用户职业, 将其分为七大类, 分别用数值1–7表示(包含企事业负责人、专业技术人员、服务业人员、文娱从事人员、教育行业、家政以及其他7类). 组合的属性信息相似度如式(7), 其中S(u, v)代表性别相似度, A(u, v)代表年龄相似度, O(u, v)代表职业相似度.

${{s}}i{m_f}(u, v) = 0.6S(u, v) + 0.1A(u, v) + 0.3O(u, v)$

(7)

1.3 融合信任因子模型

融合信任因子模型综合考虑了信任关系的潜在因素和用户个体差异, 主要包含社会信任度关系和属性特征相似度. 用户u和用户v的信任因子模型如式(8), 其中, $\alpha $ 为权重因子, $\alpha \in 0, 1$ .

${{s}}i{m_{{t}}}(u, v) = \alpha Trust(u, v) + (1 - \alpha ){{s}}i{m_f}(u, v)$

(8)

1.4 改进的相似度计算

用户之间的相似度可以使用余弦相似度来计算, 但是不同用户评分可能会有不同的评分标准, 有的用户习惯性打高分, 而有的用户习惯性打低分, 考虑到不同用户的评分偏好问题, 本文使用修正的余弦相似度作为传统相似度计算方法. 其中 $\mathop {{r_u}}\limits^{\rm{ - }} $ , $\mathop {{r_{{v}}}}\limits^{\rm{ - }} \;$ 表示用户u, v对于所有评分电影的均值, ${{{r}}_{uv}}$ 表示两个用户共同的评分集合, ${{{r}}_{u, i}}$ , ${{{r}}_{{{v}}, i}}$ 分别表示用户u, v对于电影i的评分, 修正的余弦相似度计算如下:

${{si}}{{{m}}_c}(u, v) = \frac{{\displaystyle\sum\limits_{i \in {r_{uv}}} {({r_{u, i}} - \mathop {{r_u}}\limits^ - ) \times ({r_{v, i}} - \mathop {{r_v}}\limits^ - )} }}{{\sqrt {\displaystyle\sum\limits_{i \in {r_u}} {{{({r_{u, i}} - \mathop {{r_u}}\limits^ - )}^2}} } \times \sqrt {\displaystyle\sum\limits_{i \in {r_v}} {{{({r_{v, i}} - \mathop {{r_v}}\limits^ - )}^2}} } }}$

(9)

结合本节所述, 将信任因子和修正的余弦相似度融合得到用户综合相似度sim(u, v), $\;\beta $ 为调整综合相似度的系数, $\;\beta \in (0, 1)$ , 用户相似度计算如下:

${{s}}im(u, v) = \beta {{s}}i{m_{{t}}}(u, v) + (1 - \beta ){{s}}i{m_c}(u, v)$

(10)

2 重排序多样化推荐 2.1 聚类

K-means算法是基于划分的无监督聚类算法^{[21, 22]}, 用途广泛且收敛速度快. 通过K-means聚类算法对用户进行划分, 能够将用户分为k个用户社群, 社群内用户的相似度较高, 社群间用户的相似度较低. 但是K-means算法容易受到初始聚类中心的影响^[23], 对初始聚类中心具有较高的敏感性, 而且合适的初始聚类中心的选择能够减少聚类迭代的次数, 加快收敛速度, 因此, 选择合适的初始聚类中心至关重要. 本文对K-means进行一些改进, 在选取初始类簇中心时保证其各中心之间的距离尽可能大, 然后进行聚类并不断更新类簇中心, 用户-评分矩阵聚类的步骤如算法1.

算法1. 用户-评分矩阵聚类算法

输入: 用户-评分矩阵 $\scriptstyle {R_{m \times n}}$ , 聚类的类簇个数k

输出: k个用户社群 $\scriptstyle C = \{ {C_1}, {C_2}, \cdots, {C_{{k}}}\} $

1) 随意选取一个用户作为初始聚类的中心 $\scriptstyle {C_1}$ .

2) 首先计算每个用户与当前存在的类簇中心之间最小相似度, 用D(x)表示, 则每个用户被选为下一个聚类中心的概率为 $\scriptstyle D{(x)^2}/{\sum {D(x)} ^2}$ , 按照轮盘概率法选择下一个聚类中心.

3) 重复2), 直到选出k个聚类中心 $\scriptstyle {C'} = \{ {C_1}', {C_2}', \cdots, {C_{{k}}}'\} $ .

4) 对于矩阵中每个用户u, 计算它到k个聚类中心的相似度并将其划分到最近的聚类中心所对应的簇中.

5) 针对每个类簇, 重新计算它的聚类中心 $\scriptstyle {C_i}$ .

6) 重复步骤4)和步骤5), 直到聚类中心的位置不再变化.

2.2 多样化推荐

用户的推荐列表是根据相似用户的电影评分和相似度计算得到的预测评分来推荐的. 以得到用户u的推荐列表为例, 首先需要计算目标用户u与所有聚类中心的距离, 找到距离最近的类簇. 然后计算用户u与该类簇中所有用户的相似度, 选取最近的k个邻居, 记作 ${U_{{u}}}$ , 则用户u对于电影m的预测评分计算如下:

${R_{u, i}} = \mathop {{R_u}}\limits^ - + \frac{{\displaystyle\sum\nolimits_{v \in {U_u}} {sim(u, v) \times ({R_{v, i}} - \mathop {{R_v}}\limits^ - )} }}{{\displaystyle\sum\nolimits_{v \in {U_u}} {sim(u, v)} }}$

(11)

其中, $\mathop {{R_u}}\limits^{\rm{ - }} \;$ , $\mathop {{R_v}}\limits^{\rm{ - }} \;$ 分别表示用户u, v的电影评分均分, ${R_{{{v}}, i}}$ 表示用户v对电影i的评分.

但是在计算预测评分时, 推荐算法的多样性容易受到用户活跃度的影响^[24], 如果用户比较活跃, 那么他的感兴趣范围更广, 更容易和其他用户有共同的评价电影, 但是这不能表示活跃用户的兴趣特征, 推荐的电影参考价值不大, 因此本文使用重排序技术, 通过引入惩罚因子, 使非活跃用户的推荐权重增大, 活跃用户的推荐权重减小. 重排序技术不会改变电影推荐的候选集, 只是在排序过程中改变电影的推荐概率, 把一些新物品移到推荐列表前面. 本文引入惩罚因子修正电影的推荐度, 改进后的电影预测评分计算如下:

${R_{u, i}} = \mathop {{R_u}}\limits^ - + \frac{{\displaystyle\sum\nolimits_{v \in {U_u}} {sim(u, v) \times ({R_{v, i}} - \mathop {{R_v}}\limits^ - )} }}{{\ln( 1 + |N(v)|) \times \displaystyle\sum\nolimits_{v \in {U_u}} {sim(u, v)} }}$

(12)

其中, $|N({{v}})|$ 表示邻居v的评分电影数. 用户越活跃, 其评价的电影数量就越多, 那么惩罚因子就越大, 该用户的推荐度参考性就相对更低一些.

2.3 推荐算法模型

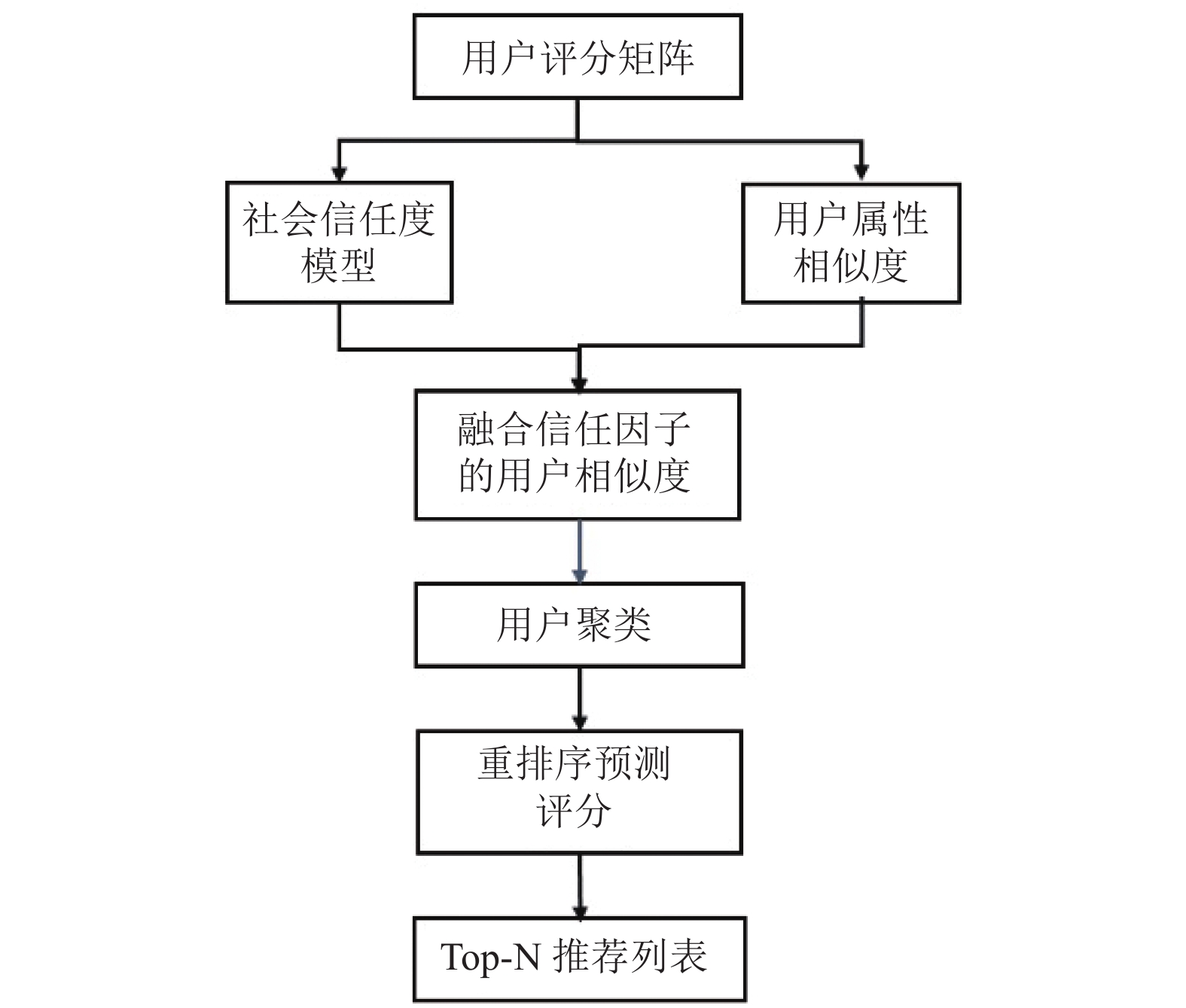
结合上文所述, 融合信任因子的多样化电影推荐算法整体的流程如图1所示.

3 实验结果与分析 3.1 实验数据集及评价指标

本实验使用美国明尼苏达大学GroupLens实验组创建的开源电影数据集Movielens-100K. 此数据集包含了943名用户对1682部电影的100 000条评分记录, 每位用户至少评分20部电影, 评分值区间为1~5, 评分越高表明用户对于电影的喜爱度越高. 同时数据集中还包含用户信息表、职业列表等, 能够对用户数据进行挖掘. 为避免偶然性, 实验采用五折交叉验证法, 将数据均分为5份, 其中1份作为测试数据集, 另外4份作为训练数据集. 重复进行实验5次, 5次实验结果的平均值为实验最终结果.

实验软件环境为Windows10 x64、PyCharm x64, 硬件环境为Intel(R) Core(TM) I5-10210U CPU @ 1.60 GHz 8核.

本文采用平均绝对误差MAE (Mean Absolute Error)^[25], 整体多样性^[26]作为算法度量标准. MAE能够衡量预测评分和真实评分的差距, 其值越小, 误差越小, 推荐准确度就越高. 其定义为:

$MAE = \frac{{\displaystyle\sum\limits_{i \in {{te}}st} {|{q_i} - {p_i}|} }}{n}$

(13)

其中, ${p_i}$ 表示目标用户u对于电影i的预测评分, ${q_{{i}}}$ 表示目标用户u对电影i的真实评分. n表示推荐的电影数量.

多样性指标^[25]显示了推荐列表中电影的多种类、非相似性, 能够覆盖到用户不同的兴趣和爱好, 推荐系统中用户u的推荐列表的多样性定义如下:

$iDiversity(R(u)) = 1 - \frac{{2 \times \displaystyle\sum\nolimits_{i, j \in R(u), i \ne j} {sim({{i}}, j)} }}{{|R(u)|(|R(u)| - 1)}}$

(14)

其中, |R(u)|表示用户u的推荐列表数目, sim(i, j)表示推荐列表中的电影i和j之间的相似度.

用户的个体推荐结果多样性越高, 系统整体的多样性越高, |U|表示用户个数, 系统整体多样性定义如下:

$D{{iversity = }}\frac{1}{{|U|}}\sum\nolimits_{u \in U} {iDiversity(R(u))} $

(15)

3.2 实验结果分析与对比

实验1. 聚类个数k, 相似度计算方法的选择.

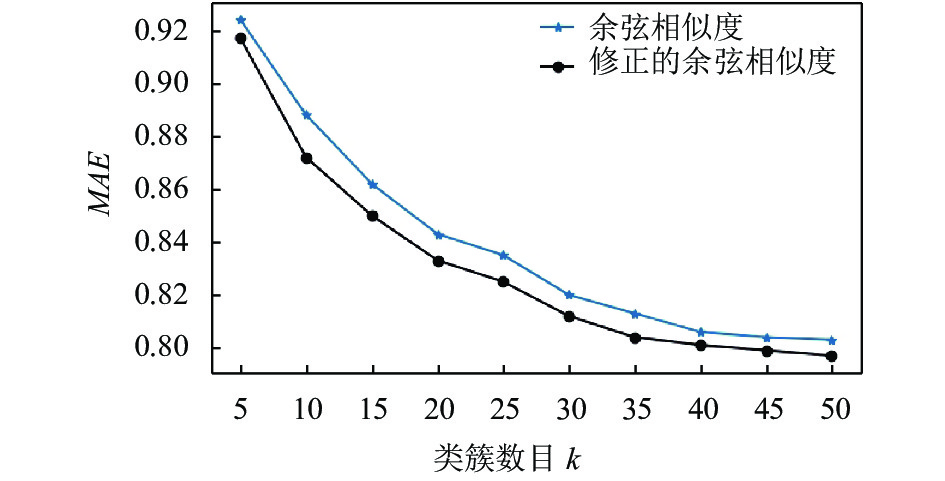
为了达到更好的推荐效果, 使用聚类算法时要确定一个合适的类簇数目k. 此处先采用传统的协同过滤方法进行实验, 相似度计算方法使用余弦相似度和修正的余弦相似度方法进行对比实验, 设置类簇的取值范围为[5, 50], 增量为5, 然后计算MAE值, 实验结果如图2.

根据实验可得出结论, 修正后的余弦相似度计算方法比余弦相似度方法得到的结果整体误差要小一些, 随着类簇数量的增多, 两种方法的MAE值减小的速度逐渐变慢趋于收敛, 故本文采用修正的余弦相似度方法作为相似度的计算方法.

在基于修正的余弦相似度方法中, 当类簇数目达到35之后, MAE值趋于平稳, 考虑到算法的计算效率, 因此选取类簇数目k为35进行实验.

实验2. 信任因子模型权重.

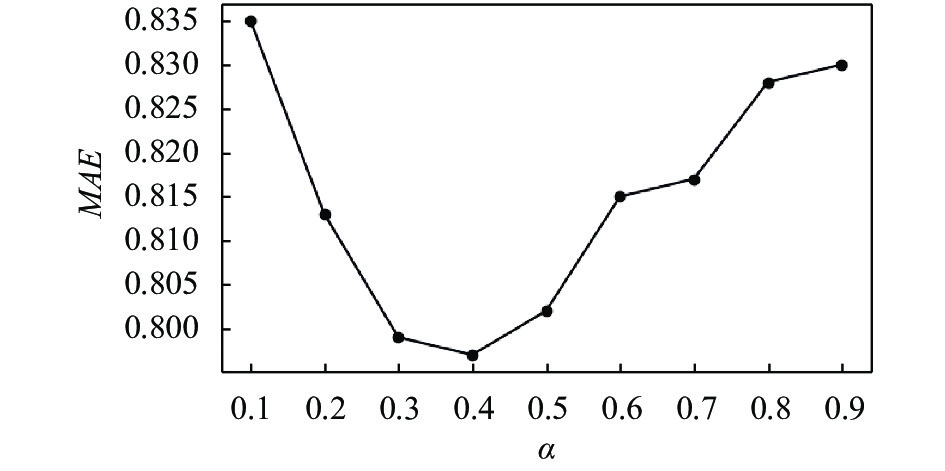
将用户的社会信任度和属性特征相似度相融合得到信任因子模型 ${{s}}i{m_t}(u, v)$ , 设置权重系数 $\alpha \in 0, 1$ , 增量为0.1, 计算不同权重下的MAE值, 结果如图3.

根据实验可知, 当 $\alpha $ 为0.4时, MAE值较小, 因此取0.4为权重系数.

实验3. 用户相似度参数选择.

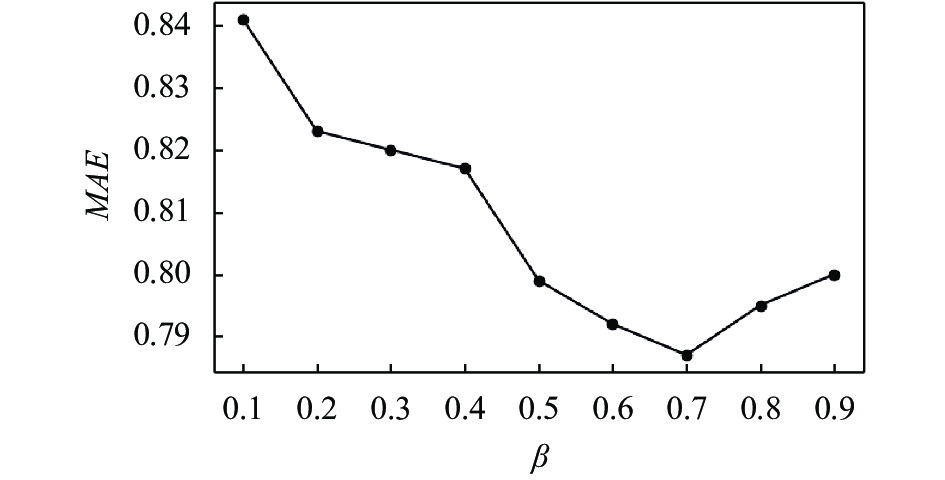
将用户的信任因子模型和修正的余弦相似度相融合得到用户相似度sim(u, v), 设置参数 $\;\beta \in (0, 1)$ , 增量为0.1, 计算不同参数下的MAE值, 结果如图4.

根据实验可知, 当 $\;\beta $ 为0.7时, MAE值较小, 因此取0.7为权重系数.

实验4. 本文算法与其他算法性能对比.

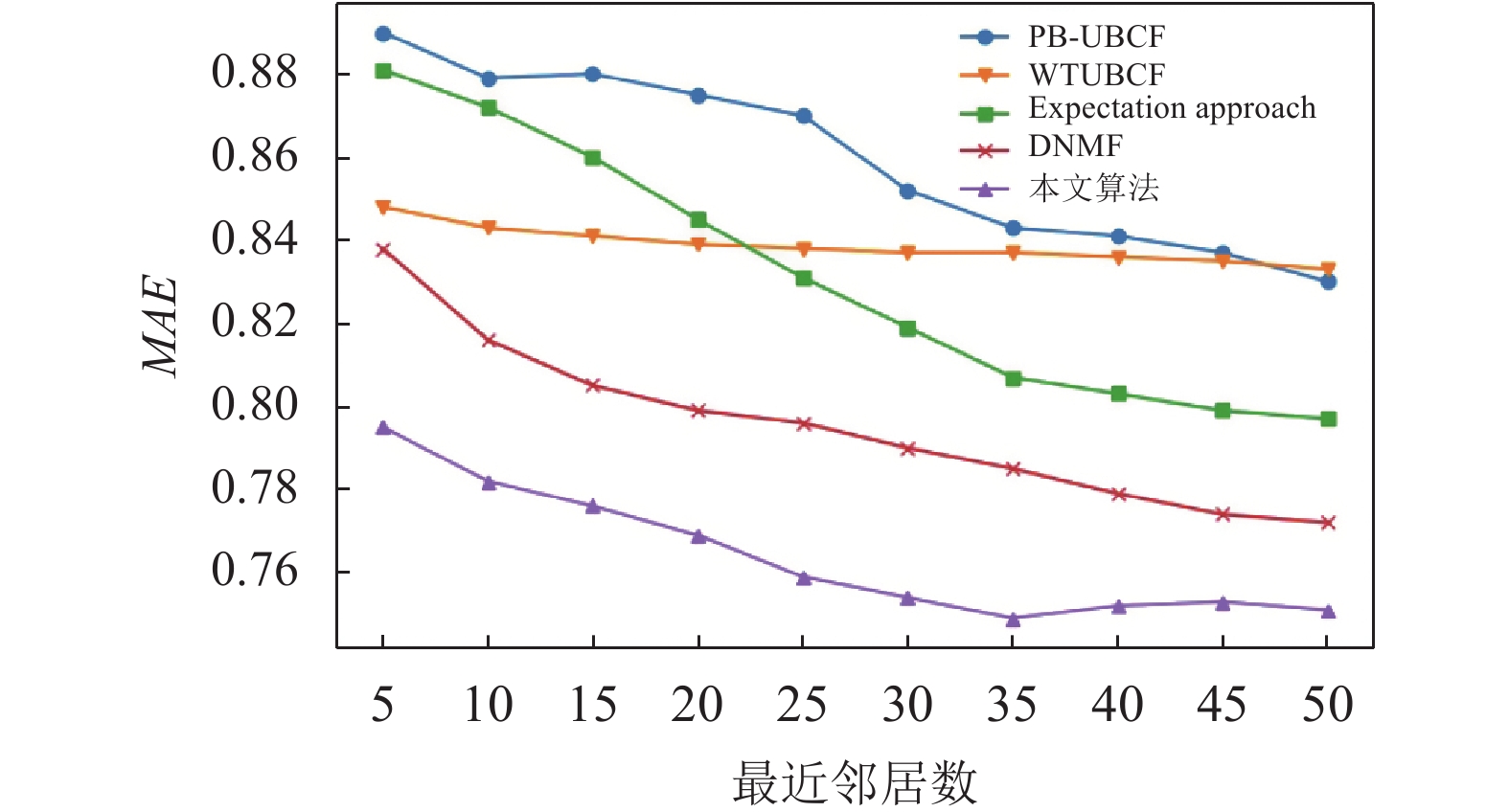
本实验选取基于皮尔逊相似性的协同过滤算法(PB-UCF), 文献[17]提出的融入用户喜好度到信任关系中的协同过滤算法(WTUBCF), 文献[27]提出的topN推荐算法Expectation approach, 文献[28]提出的DNMF算法和本文提出的算法做对比, 5种算法的最近邻居用户区间取值为[5, 50], 增量为5, 比较MAE和多样性指标.

从图5中可以看出, 本文提出的算法在最近邻居数达到35能够取得较好的推荐效果. 4种算法随着最近邻居数目的增多MAE值逐渐下降, 本文算法的MAE值明显低于其他4种算法, 说明本文提出的算法能够提高算法推荐的准确度.

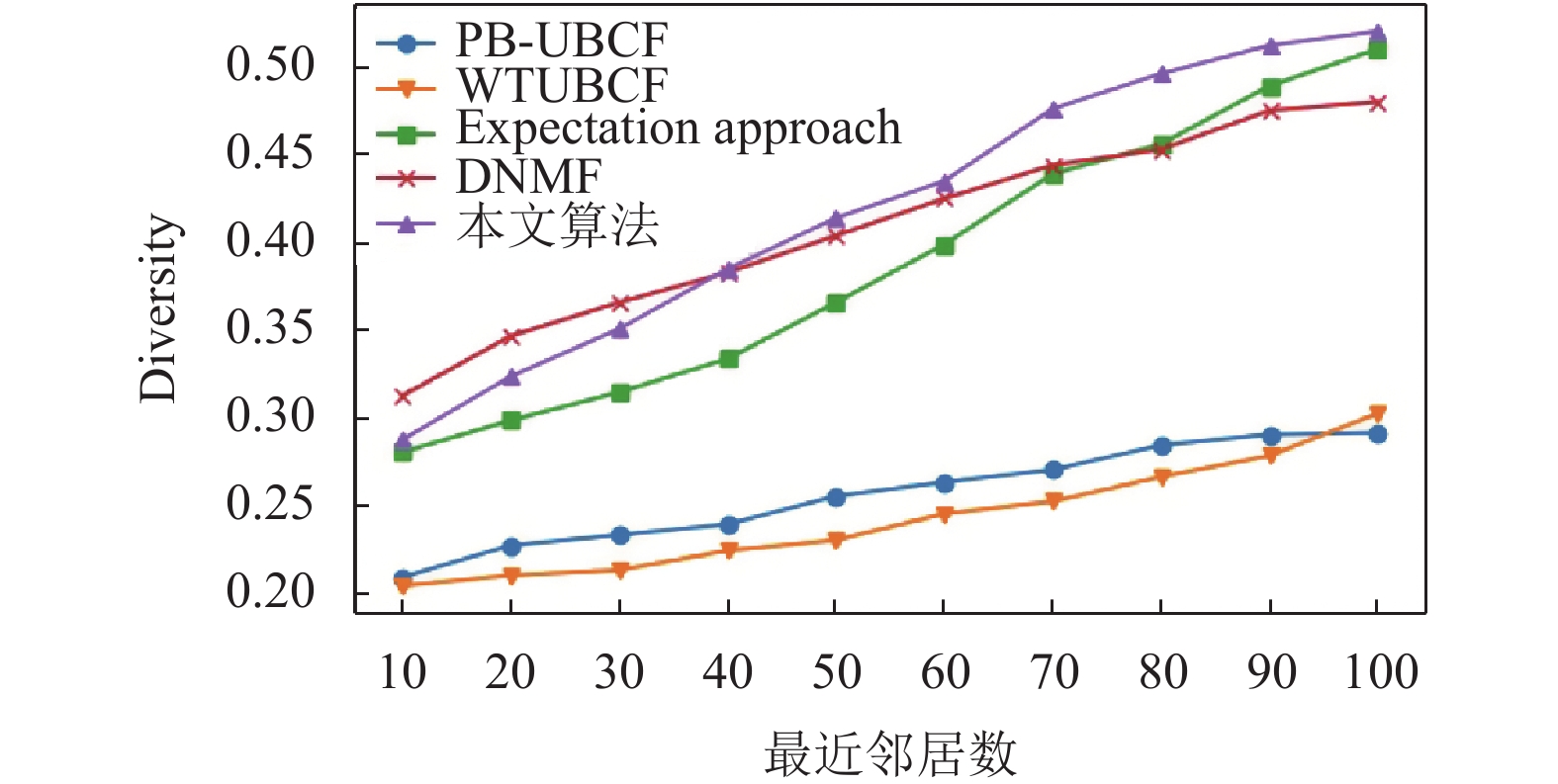
从图6中可以看出, 随着推荐物品的数量增多, 系统的多样性逐步增加. PB-UCF和WTUBCF两种算法由于没有对多样性问题进行改进, 所以算法多样性相对较低. 和Expectation approach相比, 随着最近邻居数的增加, 本文提出的算法在多样性指标中相对较高些. 在最近邻居数小于40时, DNMF算法的多样性较其他算法高一些, 在邻居数大于40后, 本文提出的算法的多样性相对较高, 可见随着推荐电影的数目的增多, 本文提出的算法能够更好地分析用户属性特征并为其提供个性化的推荐. 因此本文提出的算法在保证准确度的情况下, 能够在一定程度上提升电影推荐系统的多样性.

4 结论与展望

本文提出的融合信任因子的多样化电影推荐算法, 通过分析社会性信任度关系和用户特征信息, 充分挖掘了用户的特征信息. 另外通过引入惩罚因子, 结合用户活跃度实现了电影多样化推荐. 通过实验分析, 证明了本文提出的算法有效, 相对于之前的电影推荐算法来说, 算法平均绝对误差更小, 同时推荐算法的多样性有了相对地提升. 另外, 本文提出的算法具有一定的通用性, 除了可以用于电影推荐系统之外, 还能应用于电商推荐系统、新闻推荐系统等.

但是对于实际推荐系统, 隐式反馈对于推荐算法也起着至关重要的作用. 在接下来的工作中将会对隐式反馈进行研究, 使推荐算法更迎合用户的偏好.