2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing, 100049, China
癌细胞的基因组携带体细胞突变(somatic mutation). 体细胞突变指发生在除生殖细胞之外的人体细胞中的DNA结构上碱基对的改变, 其过程贯穿个体的整个生命周期. 体细胞突变的诱因主要有物理因素(如射线)、化学因素(如抗生素、烟草)以及生物因素(如细菌或病毒基因的融合)[1]. 如图1所示, 从受精卵第一次分裂开始, 细胞受到某种致癌因子的刺激而发生突变. 突变过程可能会引起DNA损伤和修复, 并产生单核苷酸替换(single nucleotide substitutions)、短插入和删除(short insertions and deletions)、结构变异(structure variants)和染色体拷贝数变化(copy number variation)等[2]. 各致癌因子之间相互独立, 在体细胞基因组上留下独特的记号, 随着个体生命的延续, 体细胞突变不断叠加累积, 最终使细胞脱离控制, 形成生长增殖不受限制的癌细胞. 生物医学研究中普遍认为, 细胞在正常生长分裂过程中产生的突变在基因组上是随机分布的, 而由特定致癌因子导致的突变则具有一定的模式. 这种模式能够反映细胞癌变过程中曾暴露于哪些致癌因子以及在其中的暴露程度. 研究中将基因组中由致癌因子引起的这种特有突变模式叫做突变印迹(mutational signature)[3].
早在DNA双螺旋结构被发现之前, 已有临床研究发现连续的紫外线辐射会加速细胞增殖的相对速度, 从而明确了紫外线的过量辐射是皮肤癌的一大诱因[4]. 测序技术的出现尤其是下一代测序技术(Next Generation Sequencing, NGS)的蓬勃发展, 迅速推动了分子生物学和生物信息学的研究进展[5]. 研究显示, 人的基因组序列中存在大约400万个突变位点, 全外显子组序列中可以检测到大约6万–8万个突变位点[6]. 大多数癌症中的体细胞突变属于“乘客”突变(passenger mutations), 即不导致细胞癌变, 在癌症发展的过程中也不会被正向选择. 仅有少数的突变是“驱动”突变(driver mutations), 即赋予细胞生长优势并且帮助癌细胞增殖[7].
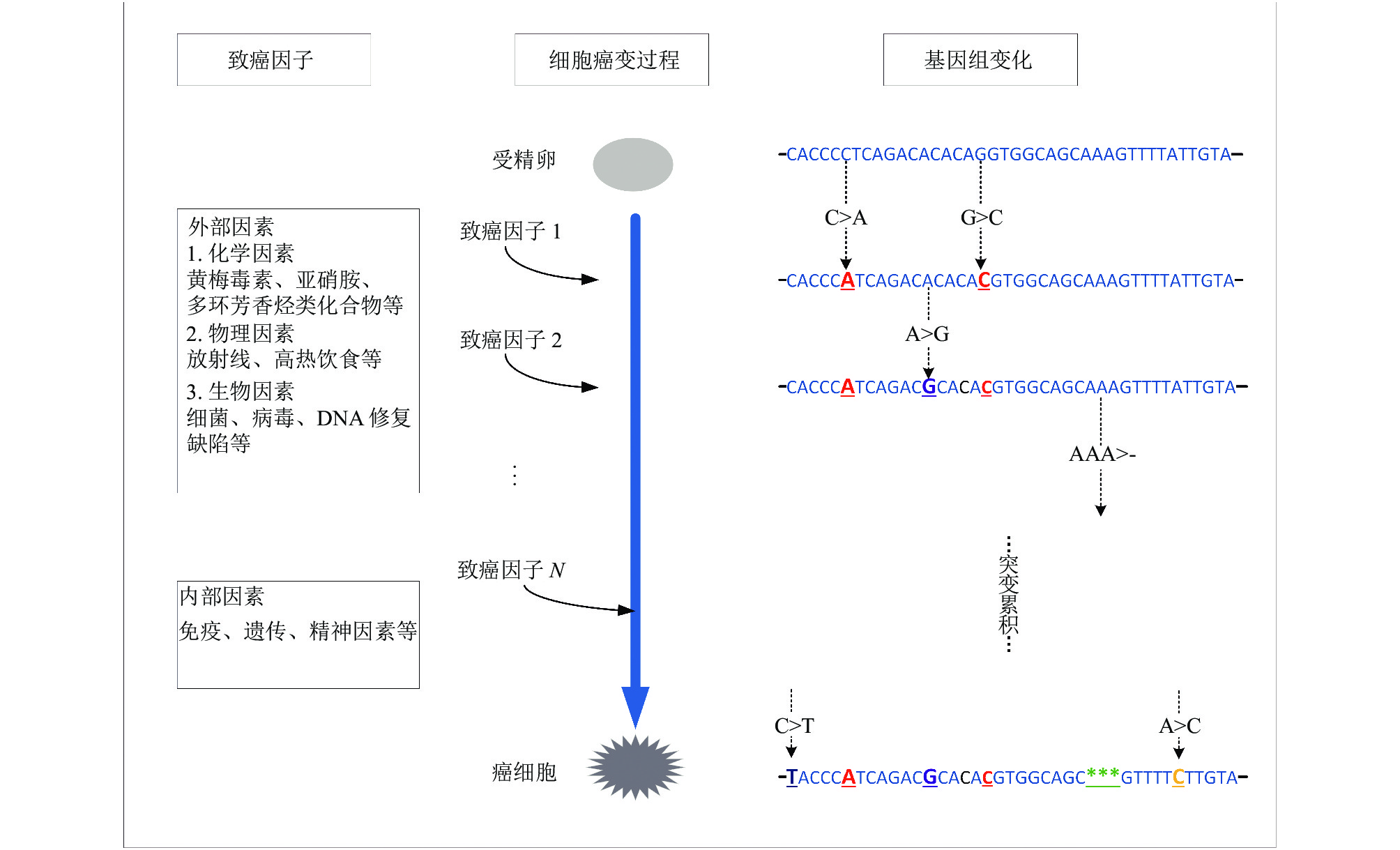
|
图 1 突变过程在癌症基因组中留下的特征性印记 |
长久以来, 对体细胞突变的研究方向局限在驱动基因(driver genes)上, 如TP53
突变印迹的概念由Alexandrov等人提出的[3], 他们在21个乳腺癌的全基因组单碱基替换突变类型中计算并提取了5个特殊的突变模式, 这些单基因替换突变并未进行“驱动”和“乘客”的区别, 而是将他们全部作为分析对象. 研究中还尝试解释了其生物学机制, 如以TpCpX三核苷酸处的C>T, C>G和C>A替换为主要特征的突变印迹是由5-甲基胞嘧啶作用自发的内源性突变过程导致的, 是癌症样本中绝大多数的突变类型, 并且以这种显性的突变形式存在于约10%的雌激素受体(Estrogen Receptor, ER)阳性乳腺癌患者中[2]. 虽然当时并未对计算出的5个印迹进行完全的生物学解释, 但该研究已经对潜在的突变机制形成了一些见解并提供了研究的思路. 2013年, Alexandrov等人又开展了一项涉及30个癌种, 7042个样本的研究, 在4938362个单碱基替换中解析出21个经过生物学验证的突变印迹[3]. 2018年, 该研究团队将研究数据集继续扩大到23829个癌症样本的4729690个体细胞突变集合上, 同时纳入了更多的突变类型: 单碱基替换, 双碱基替换, 短插入删除和结构变异. 更大规模的数据集中发现了新的突变印迹: 49种单碱基替换印迹, 11种双碱基替换印迹, 17个短插入删除印迹以及11个结构变异的聚类[9]. 这些印迹既验证了紫外线、烟草、酒精等与癌症发生相关联的外部因素, 一些新的印迹也被证实与独特的临床特征相关, 这说明突变印迹的分析很可能成为靶向治疗中新的潜在生物标志物[10].
虽然一些突变印迹反映的致癌因子(如紫外线照射、烟草)可以通过跟踪调查和统计来识别, 但是一种正式的数学方法可以提取人类难以察觉的更微妙的元素和较弱的信号, 同时还需要评估该元素或信号在癌变过程中的比例. 并且随着基因组计划的完成, 大规模的基因组测序数据也对突变印迹问题的求解提出了考验. 目前, 已有多个基于NGS的识别突变印迹的算法和软件, 但对该问题的求解在参数设置等方面尚未达成共识. 据调研, 目前缺乏关于体细胞突变印迹分析算法和软件的比较, 并且随着更多癌症突变位点的检出, 突变印迹分析将获得很大的挖掘空间. 因此, 开展该领域的相关研究, 清晰详细地介绍和讨论是十分必要的.
总体来讲, 本文的主要研究内容包括:
(1) 突变印迹问题及其数学模型阐述.
(2) 突变印迹提取算法及评价.
(3) 突变印迹提取软件的其他功能介绍.
(4) 比较总结实验结果并提出新的解决方案.
1 突变印迹的数据模型突变印迹问题可以描述为: 从复杂的体细胞突变信号中寻找独立致癌因子使基因组发生的特有的改变模式. 癌细胞基因组的改变可能是多个致癌因子引发突变的累积, 原始致癌因子使基因组发生改变的程度也不相同. 因此, 可将突变印迹问题抽象为盲源分离问题(Blind Source Separation, BSB)[11].
盲源分离问题是研究在系统的传递函数、源信号的混合系数及概率分布未知的情况下, 利用源信号之间相互独立这一微弱的已知条件, 如何从一组复杂的混合信号中分离出独立的不可观测的源信号. 盲源分离作为阵列信号处理的一种新技术, 允许有意义地学习对象的不同部分, 近几年来受到广泛关注.
盲源分离问题在突变印迹分析中的应用可以表述为算法1.
算法1. 突变印迹分离算法
1. 计算体细胞突变信号中的最优突变印迹的组合, 以表示在癌症的发展过程中每个独立突变过程的累积;
2. 计算每个印迹在每个独立癌症基因组的体细胞突变中的比例, 表示印迹对应的致癌因子对癌变过程的贡献度.
算法中原始体细胞突变信号常采用结合上下文的三碱基结构表示. 基因组是由腺嘌呤(A)、胸腺嘧啶(T)、鸟嘌呤(G)、胞嘧啶(C)组成的序列. 由于基因组正负链上的碱基以互补配对原则, 即A与T配对, G与C配对形成碱基对, 则基因组上可能出现的单核苷酸替换情况有
(1) C>A: 代表C>A和G>T两种单核苷酸替换方式;
(2) C>G: 代表C>G和G>C两种单核苷酸替换方式;
(3) C>T: 代表C>T和G>A两种单核苷酸替换方式;
(4) T>A: 代表T>A和A>T两种单核苷酸替换方式;
(5) T>C: 代表T>C和A>G两种单核苷酸替换方式;
(6) T>G: 代表T>G和A>C两种单核苷酸替换方式.
将这6种替换方式表示为如式(1)所示的单碱基替换字典V:
| $ V=\left\{\rm{[C>A],[C>G],[C>T],[T>A],[T>C],[T>G]}\right\} $ | (1) |
然后, 将其上游(5'端)、下游(3'端)各一个碱基作为其上下文(如图2中标识), 三碱基结构表示为式(2):
| $ T=\left\{5^{\prime}-X v Y-3^{\prime} \mid X, Y \in\{\rm{A, C, G, T}\}, v \in V\right\} $ | (2) |
显然, 单碱基上下文结构的表示方法有
| $ T_{n}=\left[T_{1 n}, T_{2 n}, T_{3 n },\cdots, T_{k n}\right]^{\rm T},\;\; 1 \leq k \leq 96 $ | (3) |
其中, Tkn表示与Tn关联的突变过程(第n个致癌因子)引起的第k个突变符号的频率. 因此:
| $ \sum\limits_{k=1}^{96} T_{k n}=1 ; \;0 \leq T_{k n} \leq 1,1 \leq k \leq 96 $ | (4) |
将一个癌症队列中每个患者的体细胞突变表示为如式(3)所示向量, 则该队列的突变目录即可表示为:
| $ M_{g}=\left[m_{1 g}, m_{2 g}, \cdots, m_{kg}\right] $ | (5) |
其中, 突变目录的每个元素可以近似地认为是使正常细胞发展为肿瘤细胞的潜在突变过程的特征的线性叠加, 且每个特征通过在相应过程中的暴露程度来加权, 如式(6):
| $ m_{{kg}}=\sum\limits_{n=1}^{N} s_{k n} \times e_{n g} $ | (6) |
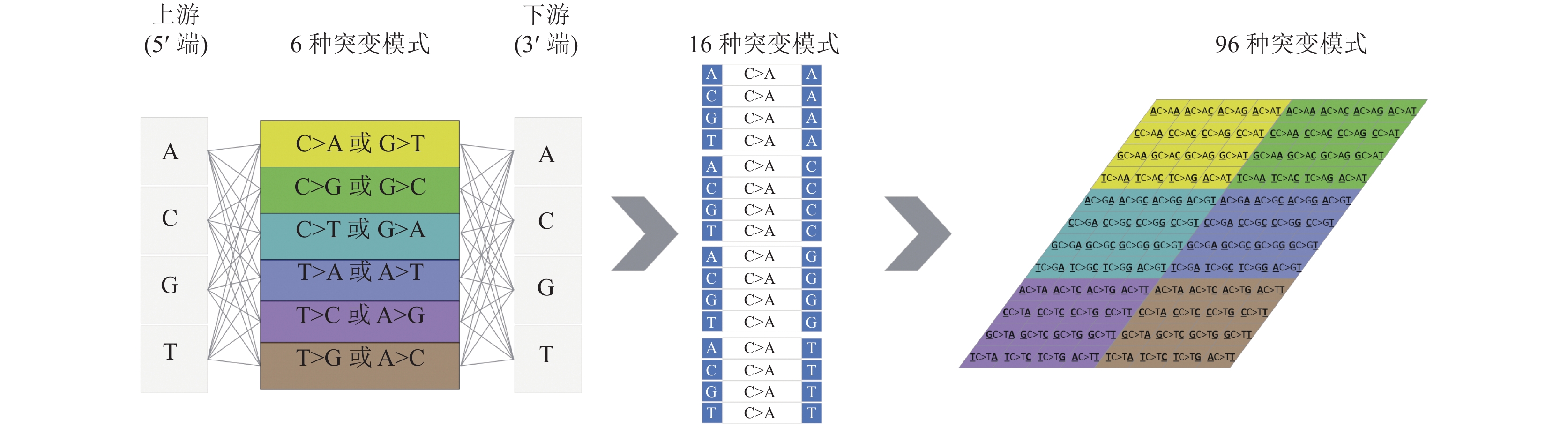
|
图 2 从体细胞突变列表中构建96种突变模式 |
因此突变印迹可通过将M 表示为两个较小的矩阵实现. 即:
| $ M\approx SE $ | (7) |
其中, M是研究队列中g个基因组的96个突变类型的突变频率:
| $ M_{k \times g}=\left[\begin{array}{c} m_{11},\; m_{12},\; \cdots,\; m_{1 g} \\ m_{21},\; m_{22},\; \cdots,\; m_{2 g} \\ \vdots \\ m_{k 1,}\; m_{k 2},\; \cdots,\; m_{k g} \end{array}\right] $ | (8) |
而Sk×n是该队列基因组由n个致癌因子导致的特定的突变模式:
| $ S_{k \times n}=\left[\begin{array}{c} S_{11},\; S_{12},\; \cdots,\; S_{1 n} \\ S_{21},\; S_{22},\; \cdots,\; S_{2 n} \\ \vdots \\ S_{k 1},\; S_{k 2},\;\cdots,\; S_{kn} \end{array}\right] $ | (9) |
En×g表示g个基因组在n个致癌因子中的暴露程度:
| $ E_{n \times g}=\left[\begin{array}{c} e_{11},\; e_{12},\; \cdots,\; e_{1 g} \\ e_{21,}\; e_{22},\; \cdots,\; e_{2 g} \\ \vdots \\ e_{n 1},\; e_{n 2},\; \cdots,\; e_{n g} \end{array}\right] $ | (10) |
此外, 突变印迹因其代表的自然意义而具有两个特征: (1)研究对象的非负性. 一个癌症队列中所有基因组体细胞突变目录M表示的是每个样本的每种突变类型的突变频率, 分解矩阵S表示突变过程的特征, 系数矩阵E表示突变过程在基因组上的强度; (2)研究目标是期望从体细胞突变目录中提取具有生物学意义的特征, 即致癌因子在基因组上留下的特殊记号.
2 算法分类和比较根据对式(7)的求解方法, 可以将突变印迹问题分为3类: 一是非负矩阵分解(Nonnegative Matrix Factorization, NMF)的方法; 二是期望最大化(Expectation Maximization, EM)方法; 三是线性回归(Linear Regression, LR)方法. 按照是否能够发现新印迹可以将突变印迹问题分为允许新印迹发现的“提取”方法和对已知印迹的“拟合”方法.
2.1 求解方法的比较 2.1.1 NMF方法NMF算法是由Lee和Seung于1999年提出的一种矩阵分解方法, 它使分解后的所有分量均为非负值,并且同时实现非线性的维数约减[12]. NMF作为从各种类型的高维生物数据中提取有意义成分的一种强大技术屡次脱颖而出. 此外在其他领域也有NMF方法的成功应用, 如“鸡尾酒会”问题, 人脸识别问题等[13]. 由于上述数学模型中矩阵的内在非负性, 使得NMF特别适合于突变特征推断问题. NMF也是第一个用来尝试分析突变印迹问题的算法. 如表1所示, 目前已有如SigProfiler、SomaticSignatures、sigfit和MutationalPatterns等多个软件基于NMF算法来解决印迹分解问题.
SigProfiler方法通过找到矩阵S和E来准确地提取N个突变印迹, 同时解决由式(7)导出的非凸优化问题. 该方法选择矩阵范数作为Frobenius重构误差:
| $ \min\limits_{S \geq 0, E \geq 0}\|M-\textit{SE}\|_{F}^{2} $ | (11) |
| 表 1 突变印迹分析软件汇总 |
以SigProfiler为代表的NMF算法具体步骤如算法2.
算法2. 以SigProfiler为代表的NMF算法
1. 初始化随机非负矩阵S, E;
2. 将初始突变目录矩阵降维, 将所有突变类型中占比≤1%的突变类型删除, 得到矩阵M′;
3. 迭代:
(1)对矩阵M′进行蒙特卡洛自举重采样(Monte Carlo bootstrap resampling), 得到矩阵M";
(2)乘法更新算法应用于M", 得到使式(11)中的Frobenius范数最小的S和E;
4. 对S划分聚类, 得到N个簇;
5. 将每个簇中的s归一化, 得到S的N个向量;
6. 求暴露矩阵E.
基于NMF方法提取突变印迹的软件需要指定分解个数N作为程序输入, SigProfiler根据大量实验给出的建议值是:
| $ N \in(1 \sim \min \{K, G\}-1) $ | (12) |
在实际操作中, SigProfiler根据每个N值计算模型的总体再现性和Frobenius范数误差. 最终需要人工干预选择N值, 使得分解的印迹矩阵S具有高度的再现性同时显示出低的总体重建误差.
2.1.2 EM 方法Fischer等人基于NMF方法从基因组内在特性出发, 应用概率模型解决突变印迹问题[14]. 基因组的内在的特性(如CpG双核苷酸的不均一分布, 拷贝数变化)会影响三碱基序列结构发生突变的可能性, 继而使模型在推断的突变模式上产生偏倚. 理论上, 使用概率模型可在求解过程中充分考虑突变发生的可能性, 能够更准确地分离出真实突变过程的印迹.
将三碱基序列结构的突变可能性表示为非0的k元组, 其中Okg表示基因组g上第k个突变类型发生突变的可能性:
| $ O_{g}=[O_{1 g}, O_{2 g}, O_{3 g}, \cdots, O_{k g}] ;\; 1 \leq k \leq 96 $ | (13) |
EM算法的目标是使包含隐变量的数据集的后验概率或似然函数最大化, 进而得到最优的参数估计. 文献[14]将突变印迹分解问题重构为一个如式(14)所示的概率模型. 其中突变目录矩阵(M)分布为独立的泊松随机变量, 其元素由印迹矩阵(S)与暴露矩阵(E)乘积确定, 通过期望最大化算法对S和E进行估计.
| $ P\left(M_{g} \mid E_{g}, O_{g}, S\right) \equiv \prod\limits_{k=1}^{K} P o i s\left(m_{k} \mid O_{k} \sum\limits_{j=1}^{x} s_{k} v_{n g}\right) $ | (14) |
算法的具体执行过程如算法3.
算法3. 以EMu为代表的EM算法
1. 猜想模型参数S(0);
2. 迭代
(1)给定当前猜测参数S(k), 得到曝光估计值
(2)使用
(3)当P(M|S)收敛到极大值时, 迭代结束;
3. 比较不同N下的数据可能性, 确定突变过程数量.
值得注意的是, 虽然EMu是建立在对NMF的有效替代解释的基础上, 该解释将NMF视为对特定问题的EM应用, 但EMu的新概念和优点并不是固有的EM范例特性, 也可以通过其他方法进行同化的显式增强. 另一方面, EMu对初始条件的敏感度与常规NMF相同. 尽管如此, EMu成功地利用了突变印迹推断的概率形式来解决以前未曾探索过的方向, 即结合了基因组的内在特性和肿瘤特定的突变可能性并确定了突变印迹的个数.
2.1.3 LR方法线性回归(Linear Regression, LR)指通过对大量的观测数据进行处理, 从而得到比较符合事物内部规律的数学表达式[15]. 在NMF方法发现了一些可解释的突变印迹的基础上, 印迹提取问题可扩展为新的描述: 对某个癌症队列的研究不再需要发现新的印迹, 而重点在于得到肿瘤中存在的、可解释的印迹以及其对癌症发展的作用程度. 因此, 突变印迹提取转变为对已知突变印迹分布的拟合, 即对线性方程(15)的求解.
| $ M=\textit{SE}+R $ | (15) |
由于线性回归方法对先验知识的依赖, 尤其依赖对已知突变印迹的个数选择和组合, 导致其在实际应用中十分受限, 如目前已知的突变印迹集尚不能完全地解释癌变过程, 个别突变印迹没有得到完备的生物学解释等. 同时研究中也指出该方法的准确性偏低, Maura等人在2019年的研究中发现, 使用同样的突变目录(M)情况下, 非负矩阵分解算法提取的突变印迹大部分能够被验证其所代表的生物学意义, 而使用线性回归方法拟合的突变印迹大多为“无特征”或“平坦”印迹, 即6种突变模式的频率分布相对均匀, 无明显差异[16].
2.2 “提取”算法和“拟合”算法表1中的软件和算法分别从不同角度出发来解决印迹问题, 根据算法特征及必需的输入数据, 可将其分为印迹“提取”算法和“拟合”算法. 基于NMF的“提取”算法以突变目录矩阵M和分解个数N为输入, 求解印迹和暴露矩阵, 因此分解出的印迹矩阵S中可能会出现新的印迹. 与提取方法不同, 拟合方法以目录矩阵M和已知的印迹矩阵S为输入, 将M中潜在的印迹拟合为S的线性表达.
“提取”的方法的优势是不依赖先验知识(已知的突变印迹), 同时允许提取出新的突变印迹. 该算法也存在局限性. 首先, 同时发生的多个独立的突变印迹可能会被合并为一个印迹. 其次, 对于非常复杂的印迹可能会因其较小的贡献度而拆分为两个或多个印迹.
反之, “拟合”的方法依赖大量先验知识, 如分析的癌种有哪些致癌因子, 这些致癌因子的突变印迹分别是什么等. 现有公开发布的突变印迹总计有81种, 且50%尚未得到生物学解释, 突变目录矩阵本身的大小以及疾病类型乃至分型都会对印迹个数和组合的选择产生影响. 由于其对已知突变印迹的依赖, 因而不能发现新的印迹. 此外, 当主观性较强的先验知识被输入时, 很可能导致过拟合现象, 即夸大某个印迹在该癌种发生发展中的权重. 反之, 抛弃先验知识的限制, 将全部已知的突变印迹作为输入, 则会导致特异性突变印迹的渗透, 即少量样本的突变印迹分配至整个队列的样本中或拟合到并未在癌种的发生发展中起作用的印迹上.
同时, 两类算法也存在共性问题, 当不同的突变印迹的组合可解释同一个突变目录矩阵时, 印迹提取就会变得不明确; 当队列中存在少量异质性较高样本时, 其突变印迹因贡献度不高而被过滤掉, 从而掩盖队列的异质性.
3 突变印迹分析软件的其他功能在实际应用中, 除了对式(7)的求解外, 突变目录矩阵的构建、突变印迹及暴露矩阵的可视化、运行环境等问题在生物信息学领域也是广受关注的需求.
获取突变上下文是构建突变目录矩阵的关键. 基于NGS的突变识别软件如VarScan2[17]、Strelka2[18]、SomaticSniper[19]等给出的突变并不包含上下文信息. 有些软件如VarDict[20]在INFO列使用“LSEQ”和“RSEQ”分别给出突变上下文, 但大多数的软件不能提供此信息, 需要重新计算. 可解决的方案是利用突变位置从参考基因组中获取上下文. 但是人类的参考基因组有超过30亿个碱基, 分别计算一个基因组中上百万个突变位点的上下文需要一定的时间消耗. 此外, 通过突变注释软件(如Oncotator[21])能够获得上下文碱基序列, 然而这就需要在计算突变印迹前先对突变列表进行注释, 增加了构建突变印迹分析流程的复杂性. 因此很多软件在内部增加了计算上下文的过程, Pedersen等人开发了对VCF快速处理的Python程序Cyvcf2, 可实现快速的VCF文件处理[22].
突变印迹和暴露矩阵可视化也是基因组数据挖掘的重要内容. 除了EMu外, 目前用于计算突变印迹的软件都提供了模块化的可视化方法. 这些可视化方法都直接使用各自的分析结果作为输入, 在实际操作中无需分析人员具备专业的绘图知识.
最后, 基因组数据挖掘软件大多依赖Linux环境, 需要操作人员具备在Linux环境下编译、安装和运行软件的能力. 因此, 除了发布软件包, 多个软件如PMSignature、MutaGene等提供了门户网站的计算方式, 这在很大程度上方便了缺少计算机知识的生物医学研究人员, 同时这也是整个生物信息学领域软件的发展趋势.
4 实验分析 4.1 数据说明本文选择了21个宫颈癌的全基因组测序数据, 分别使用基于非负矩阵分解算法的软件SigProfiler[3]和基于线性回归方法的软件Mutalisk[23]分析突变印迹. 由于基于期望最大化的方法需要关键的先验知识(基因组序列的复杂性), 本文实验中不包括对EM算法的实验.
4.2 实验过程SigProfiler的实验过程如下:
(1) 构建体细胞突变目录矩阵;
(2) 将最大提取印迹数设置为10, 即N的最大取值为10;
(3) 运行SigProfiler;
(4) 选择结果稳定性高且残差相对较小的突变印迹的个数的最大值N′;
(5) 提取N'个突变印迹, 构成集合S;
(6) 计算S中每个印迹与公开发表印迹的相似性.
Mutalisk的实验过程如下:
(1) 合并21个基因组的突变识别格式文件;
(2) 选择COSMIC的30个突变印迹作为先验输入S;
(3) 运行Mutalisk;
(4) 选择文献中记载的与宫颈癌相关的印迹作为先验输入S′;
(5) 再次运行Mutalisk.
4.3 实验结果图3表示了对21个癌症患者的体细胞突变目录矩阵进行NMF分解时, 不同的突变印个数对应的突变印迹稳定性(左)和原始突变目录矩阵的重建误差(右).
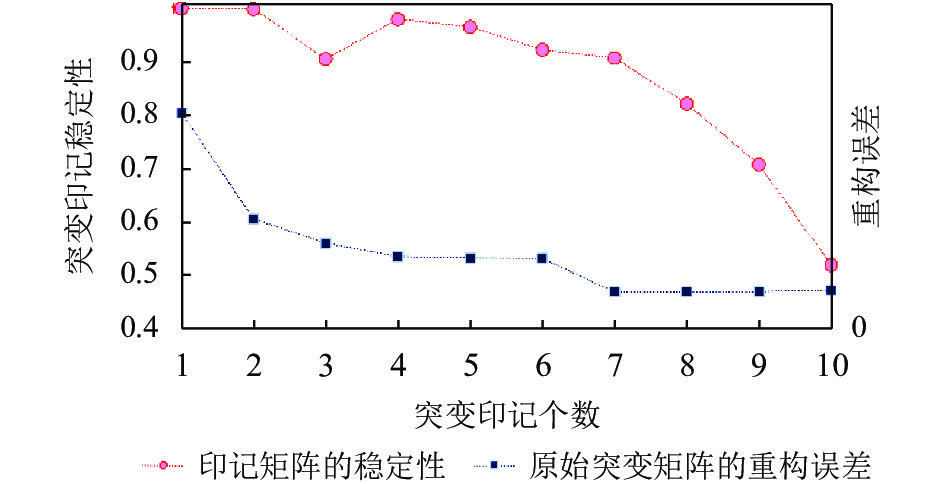
|
图 3 突变印迹数对应的突变印迹稳定性和重建误差 |
实验中, 将分解印迹数N设置为[1,10], 对每个N的取值分别计算两个指标, 最终选择再现性高且重建误差小的印迹个数. 通过图3可以看出, 当突变印迹数N<7时, 随着N的增大, 再现性逐渐降低(N=3)除外, 重构误差逐渐降低, 而在N>7时, 再现性显著降低, 重构误差稳定. 因此, 为了同时保证印迹矩阵的稳定性高和原始矩阵的重构误差低, 选择印迹个数为7.图4表示了具体7个突变印迹.
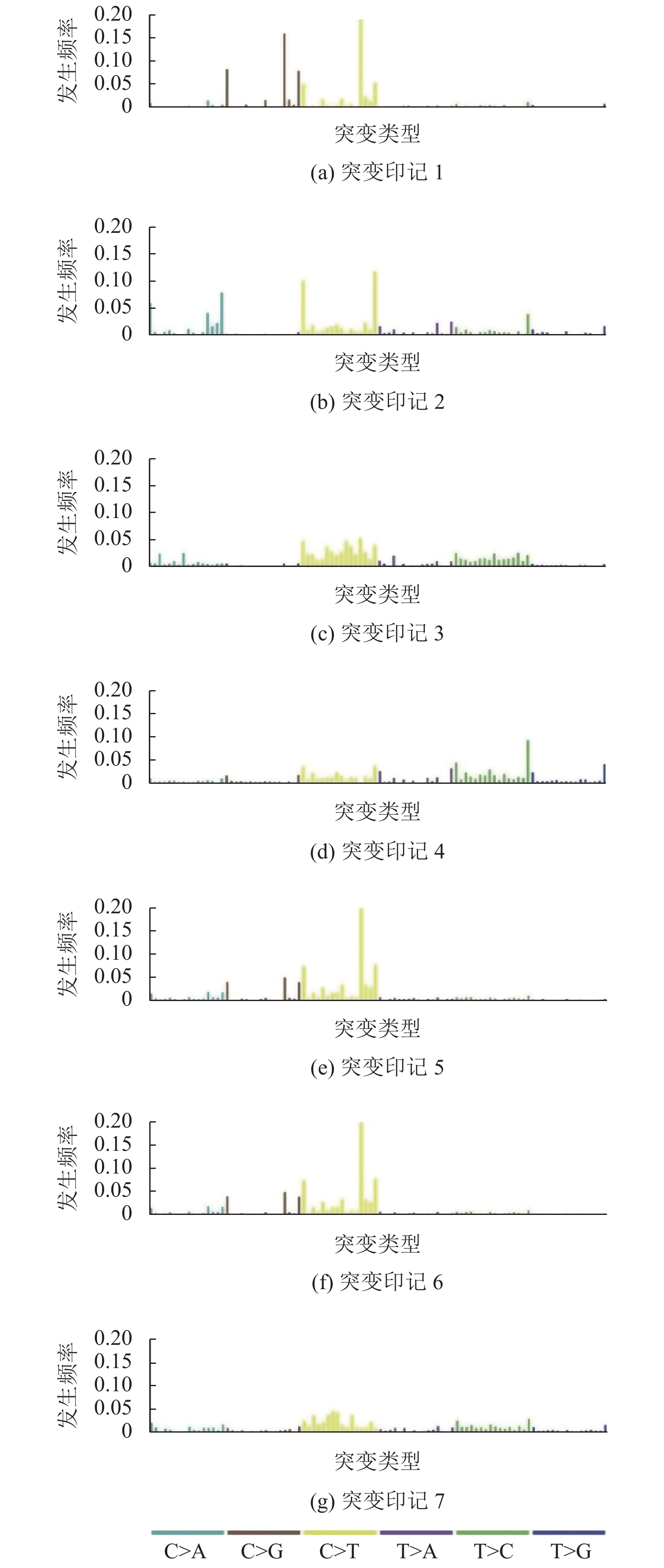
|
图 4 21个癌症基因组中提取的7个突变印记 |
为了说明提取的7个印迹与该癌种发病之间的关系, 计算了7个突变印迹与国际公开数据库COSMIC(Catalogue Of Somatic Mutations In Cancer)中2017年收录的已知30种突变印迹的余弦相似性以及可能的生物学解释(表2).
表3是Mutalisk采用30个COSMIC[24]的印迹为输入时的结果, 其将21个宫颈癌基因组的突变目录拟合到S5, S2, S13, S8, S1, S28六个已知印迹中.
当选择已知相关印迹(S1, S2, S5, S6, S8, S10, S13, S26)为先验知识时, Mutalisk给出5种拟合结果. 其中选择贝叶斯信息准则(Bayesian Information Criterion, BIC)最小的拟合结果, 即S5, S2, S13, S1, S6 (表4).
| 表 2 SigProfiler提取突变印迹与已知印迹相似性 |
| 表 3 Mutalisk 与已知30种拟合印迹情况及相似性 |
| 表 4 Mutalisk与已知6种印迹拟合情况及相似性 |
4.4 实验总结
通过对比表2至表4中的余弦相似性可知, 基于非负矩阵分解的软件SigProfiler发现的印迹与国际研究公开的印迹相似性均高于基于线性回归的拟合方法. 虽然SigProfiler提取的2, 6, 7并未得到相应的生物学解释, 但其余4个印迹分别与APOBEC基因家族和吸烟有关. 既往研究显示, APOBEC基因家族的突变印迹存在于乳腺癌、宫颈癌、肺癌等多个癌种, 其在慢性炎症条件下的异常表达可能误伤人类本身的基因组[25].
此外, 基于线性回归的拟合方法虽然也拟合到了APOBEC基因家族, 但其相似性极低. 当使用先验知识干预时, 相似性有微弱的提升, 但并不具有统计效力. 同时, 先验知识的加入使得拟合结果中过滤掉了印迹8和28, 出现了印迹6, 而印迹6是一个“平坦”印迹, 所以先验知识的加入也没有使得拟合出现可接受的结果. 最后, 该实验验证了在印迹分析问题中, NMF方法比LR方法适用性更强.
5 结束语本文全面详尽地探讨了体细胞突变印迹分析的相关概念和模型, 并对算法进行了说明, 分类和比较; 阐述了基因组测序数据进行突变印迹提取的注意事项和缺陷. 此外, 使用真实的基因组数据全面而详细地示范了如何在癌症基因组的研究中应用突变印迹分析.
本文介绍的分析框架使用了一些重要的限制和假设来描述基因组上的突变. 因此, 目前已经提取到的突变印迹仍然是数学近似值, 其轮廓可能受到所用数学方法的影响. 从概念和使用的简单性出发, 研究中假设一个印迹与某个致癌因子引起的特定突变过程相关联, 并以均一化的形式来表示. 然而, 不同的数学方法可以发现具有相似性和差异性的印迹, 并且这些印迹已通过多种方式得到证实. 随着突变数量的增加和不同类型突变之间的数量级差异, 单一数学方法可能无法实现准确的印迹分离, 因此结合充分的先验知识, 进一步研究破译和鉴定突变印迹的方法是避免产生在生物学上不可信或难以解释结果的有效手段.
突变印迹的研究已经发现了一些诱导癌症发生发展的原因, 人类癌症中自然发生的突变特征很可能有相当一部分已经被描述出来. 然而, 一些罕见的或者由治疗导致的突变印迹可能还没有被捕捉到, 需要进行彻底的探索. 目前许多最新发现的印迹背后的机制尚未明确, 还有待进一步地实验和理解. 未来, 突变印迹的提取还应该包含更多的突变类型, 无论是致病型还是继发型, 同时也包括由遗传导致的癌症易感基因中的种系突变. 这些印迹背后的诱因对于癌症预防和公共卫生具有重要意义.
| [1] |
冯娟. 癌症病因新进展: 更多体细胞突变基因被鉴定. 生理科学进展, 2007, 38(2): 173-173. DOI:CNKI:SUN:SLKZ.0.2007-02-024 |
| [2] |
Nik-Zainal S, Alexandrov LB, Wedge DC, et al. Mutational processes molding the genomes of 21 breast cancers. Cell, 2012, 149(5): 979-993. DOI:10.1016/j.cell.2012.04.024 |
| [3] |
Alexandrov LB, Nik-Zainal S, Wedge D, et al. Deciphering signatures of mutational processes operative in human cancer. Cell Reports, 2013, 3(1): 246-259. DOI:10.1016/j.celrep.2012.12.008 |
| [4] |
Rusch HP, Baumann CA. Tumor production in mice with ultraviolet radiation. The American Journal of Cancer, 1939, 35(1): 55-62. DOI:10.1158/ajc.1939.55 |
| [5] |
Reis-Filho JS. Next-generation sequencing. Breast Cancer Research, 2009, 11(3): S12. DOI:10.1186/bcr2431 |
| [6] |
Dewey FE, Grove ME, Pan CP, et al. Clinical interpretation and implications of whole-genome sequencing. JAMA, 2014, 311(10): 1035-1045. DOI:10.1001/jama.2014.1717 |
| [7] |
Bozic I, Antal T, Ohtsuki H, et al. Accumulation of driver and passenger mutations during tumor progression. Proceedings of the National Academy of Sciences of the United States of America, 2010, 107(43): 18545-18550. DOI:10.1073/pnas.1010978107 |
| [8] |
Olivier M, Hollstein M, Hainaut P. TP53 mutations in human cancers: Origins, consequences, and clinical use. Cold Spring Harbor Perspectives in Biology, 2010, 2(1): a001008. DOI:10.1101/cshperspect.a001008 |
| [9] |
Bailey MH, Tokheim C, Porta-Pardo E, et al. Comprehensive characterization of cancer driver genes and mutations. Cell, 2018, 173(2): 371-385. DOI:10.1016/j.cell.2018.02.060 |
| [10] |
Pittet JF, Mackersie RC, Martin TR, et al. Biological markers of acute lung injury: Prognostic and pathogenetic significance. American Journal of Respiratory and Critical Care Medicine, 1997, 155(4): 1187-1205. DOI:10.1164/ajrccm.155.4.9105054 |
| [11] |
Cao XR, Liu RW. General approach to blind source separation. IEEE Transactions on Signal Processing, 1996, 44(3): 562-571. DOI:10.1109/78.489029 |
| [12] |
Lee DD, Seung HS. Learning the parts of objects by non-negative matrix factorization. Nature, 1999, 401(6755): 788-791. DOI:10.1038/44565 |
| [13] |
Wang YX, Zhang YJ. Nonnegative matrix factorization: A comprehensive review. IEEE Transactions on Knowledge and Data Engineering, 2012, 25(6): 1336-1353. DOI:10.1109/TKDE.2012.51 |
| [14] |
Fischer A, Illingworth CJR, Campbell PJ, et al. EMu: Probabilistic inference of mutational processes and their localization in the cancer genome. Genome Biology, 2013, 14(4): 1-10. DOI:10.1186/gb-2013-14-4-r39 |
| [15] |
Cohen J, Cohen P, West SG, et al. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences. New York: Routledge, 2013.
|
| [16] |
Maura F, Degasperi A, Nadeu F, et al. A practical guide for mutational signature analysis in hematological malignancies. Nature Communications, 2019, 10(1): 2969. DOI:10.1038/s41467-019-11037-8 |
| [17] |
Koboldt DC, Zhang Q, Larson DE, et al. VarScan 2: Somatic mutation and copy number alteration discovery in cancer by exome sequencing. Genome Research, 2012, 22(3): 568-576. DOI:10.1101/gr.129684.111 |
| [18] |
Saunders CT, Wong WSW, Swamy S, et al. Strelka: Accurate somatic small-variant calling from sequenced tumor-normal sample pairs. Bioinformatics, 2012, 28(14): 1811-1817. DOI:10.1093/bioinformatics/bts271 |
| [19] |
Larson DE, Harris CC, Chen K, et al. SomaticSniper: Identification of somatic point mutations in whole genome sequencing data. Bioinformatics, 2012, 28(3): 311-317. DOI:10.1093/bioinformatics/btr665 |
| [20] |
Lai ZW, Markovets A, Ahdesmaki M, et al. VarDict: A novel and versatile variant caller for next-generation sequencing in cancer research. Nucleic Acids Research, 2016, 44(11): e108. DOI:10.1093/nar/gkw227 |
| [21] |
Ramos AH, Lichtenstein L, Gupta M, et al. Oncotator: Cancer variant annotation tool. Human mutation, 2015, 36(4): E2423-E2429. DOI:10.1002/humu.22771 |
| [22] |
Pedersen BS, Quinlan AR. Cyvcf2: Fast, flexible variant analysis with Python. Bioinformatics, 2017, 33(12): 1867-1869. DOI:10.1093/bioinformatics/btx057 |
| [23] |
Lee J, Lee A, Lee JK, et al. Mutalisk: A Web-based somatic MUTation AnaLyIS toolKit for genomic, transcriptional and epigenomic signatures. Nucleic Acids Research, 2018, 46(W1): W102-W108. DOI:10.1093/nar/gky406 |
| [24] |
Bamford S, Dawson E, Forbes S, et al. The COSMIC (Catalogue Of Somatic Mutations In Cancer) database and website. British Journal of Cancer, 2004, 91(2): 355-358. DOI:10.1038/sj.bjc.6601894 |
| [25] |
Roberts SA, Lawrence MS, Klimczak LJ, et al. An APOBEC cytidine deaminase mutagenesis pattern is widespread in human cancers. Nature Genetics, 2013, 45(9): 970-976. DOI:10.1038/ng.2702 |
 2021, Vol. 30
2021, Vol. 30


