随着工业制造智能化的快速发展, AGV小车在智能制造车间得到越来越多的应用. AGV在车间中负责物流任务的转运, 目前, 购买的AGV已具有安全避障、路径规划等功能. 但是, 不同AGV小车物流任务的选择和每个小车运输物流任务的顺序会得到不同的总运输路程和物流任务等待被转运的时间, 进而影响车间的生产效率和经济效益.

物流调度优化技术的关键是实现车间生产高效率、高灵活性和物流运输成本最低. 即一方面降低工位等待运输物流任务的时间, 保证物流任务运输的及时性, 以可以充分利用车间的生产设备和保证生产车间高效平稳的工作. 另一方面优化物流任务配送路径, 使得转运设备行驶最少的路程来满足工位物流任务的运输需求. 因此, 如何有效地使用调度优化算法, 以提高工位的满意度, 并达到最低生产成本, 最大化运输资源利用率, 是提高企业生产效率和经济效益的重要方法.

制造车间物流调度通常会涉及多个优化目标, 如最小化单个物流任务配送成本^[1]、最小化物流任务配送延迟时间^[2]、最小化总能源消耗^{[3, 4]}等, 多个目标之间通常会存在竞争关系, 无法使多个目标同时达到最优, 即一个目标函数值的增加可能会导致其它目标函数值的降低. 对多目标问题进行优化时, 通常有两种方式, 一是通过给每个目标函数设置一定的权值进行加权求和转换为单目标问题, 二是求得Pareto最优解集^[5]. 由于在优化过程中无法确定各目标函数的权值, 所以本文采用第二种方法进行多目标优化问题的研究.

近年来, 关于制造车间含AGV多目标调度优化已有大量的研究. 杨智飞等^[6]基于遗传算法, 融合差分进化算法同时优化完工时间、AGV数量和惩罚成本. 宋存利^[7]提出了一种改进的NSGA-II算法实现了混合流水车间最小化能耗和最小化最大完工时间的求解. Mousavi等^[8]设计了模糊混合遗传粒子群算法, 以最小化最大完工时间和最小化AGV数量为目标函数构建模型, 对柔性制造系统(Flexible Manufacturing System, FMS)中的多目标AGV调度模型进行优化. Zhang等^[9]提出一种基于实时多源制造数据的车间物料搬运动态优化方法, 设计开发了基于AGV小车、实时信息交换和物料搬运任务优化的动态优化模型, 根据小车的实时状态, 将最优物流任务分配给最优小车. Zhang等^[10]设计了基于变邻域局部搜索策略的混合遗传算法, 实现了包含最小化总加权拖期和最小化总能源消耗的作业车间调度问题求解. 张连超等^[11]通过使用灰色理论来预测物料的需求时间, 并使用时间窗构建多模型交互机制以避免小车行驶过程中的碰撞问题. Umar等^[12]设计了动态混合多目标进化算法, 研究FMS中作业和AGV的综合调度, 制定作业调度计划和确定AGV的行驶路径. Lu等^[13]提出一种混合多目标回溯搜索算法(Hybrid Multi-Objective Backtracking Search Algorithm, HMOBSA)实现置换流水车间最小化完工时间和最小化能耗的求解. 魏永来等^[14]提出一种混合禁忌蝙蝠算法, 求解以AGV总行驶路程、总运输时间和总配送成本为目标的多AGV作业车间调度优化问题. 刘二辉等^[15]提出一种改进的花授粉算法实现车间最小化工件的最大完工时间和最大化AGV利用率的求解.

综上所述, 制造车间中含AGV多目标调度优化已有大量研究, 但是已有研究中缺少对车间中一些实际因素的考虑, 建立的模型没有同时考虑AGV的能耗、物流任务的优先级、物流任务间的物流成本和工位物流任务的满意度对物流调度的影响, 与制造车间生产物流的实际情况不符. 此外, 目前混合变邻域遗传算法在车间物流调度优化问题方面的应用研究较少.

遗传算法是一种基于自然进化和选择机制的智能优化算法, 具有全局优化能力强、速度快、易于实现等优点, 但是其存在易早熟、早收敛等缺陷. 变邻域搜索算法是基于邻域结构集而非单个邻域的局部搜索算法, 其基本思想是在搜索过程中系统地改变邻域结构集来拓展搜索能力, 以提高算法局部搜索能力, 避免算法陷入局部最优, 比传统的固定邻域搜索的搜索能力更强^[16], 已用于很多优化问题的求解.

因此, 本文结合遗传算法全局搜索能力强的特点和变邻域搜索算法局部搜索能力强的特点, 并添加保优记忆库对精英个体进行保护, 设计了混合变邻域搜索的改进遗传算法VNSGA-II. 以最小化物流任务时间惩罚成本和最小化运载小车的总行驶距离为优化目标, 构建离散化车间多目标物流调度优化模型. 由于初始种群的生成方式对算法的搜索效率和解质量有较大的影响, 本文改进了初始种群的生成方式, 以物流任务优先级从高至低排序和随机生成相结合的方式生成初始种群. 在迭代过程中, 通过使用NSGA-II的虚拟适应度评估方法, 对种群中的个体进行非支配分层以及计算各层内个体间的拥挤距离, 以此评估个体的优劣. 并针对本文所构建模型的特点, 设计6个随机搜索邻域结构可有效提高解的质量, 促使种群快速跳出局部最优. 由于在变邻域搜索时会花费较多时间, 所以本文在种群最优解质量经过规定的迭代次数后没有改进时, 才对当代最优解进行变邻域搜索. 为了进一步降低物流成本和工位的满意度, 提出了基于关键AGV小车的插入邻域和基于关键物流任务的交换邻域的调整策略以进一步优化模型.

1 问题描述与数学建模 1.1 问题描述

本文研究含多AGV的离散化车间物流调度优化问题, AGV在车间中负责物流任务的运输. 某加工车间有 $k$ 个工位, 根据生产作业排程结果和工件加工工艺的要求, 每个工件加工时间、加工刀具、工装和所需物料已给定. 由于制造车间生产过程存在不确定性, 在物流配送环节, 随着时间的推移, 各个工位的物流任务会发生变化.

每个工位有进料位和出料位, 车间中还额外设置一个公共缓冲区, 该公共缓冲区服务于所有加工工位. 每个工位的进料位容量为 $c{i_k}$ , 出料位容量为 $c{o_k}$ , 当前一道工序的加工工位出料位容量达到上限, 需要将出料位的工件运走, 如果此时下一个工位的入料位已被占用, 则需要将工件运送到缓冲区. 当下一道工序的加工工位进料位有空闲时, 将工件从缓冲区运输到下一个加工工位的进料位.

物料是装在空载具中运输的, 小车每次运输一个载具的物料, 设有 $u$ 种载具, ${n_{uy}}$ 表示载具 $u$ 能装 $n$ 个物料 $y$ . 本文的物流配送任务分为两类: 主动物料配送是系统通过工位的生产加工实时数据, 计算工位原材料的消耗量, 进而得出加工工位进料位的剩余容量, 主动进行原材料的配送, 保证工位有合适数量的原材料, 又不会造成原材料到达工位没有地方存放的死锁情况, 确保了生产过程的正常运行; 准时化物料配送是根据工位的实时呼叫信息进行物料的配送, 包含了工件、刀具、工装、成品和空载具. 物流调度目标为采用 $i$ 辆小车根据需求将物料从物流起点运输到物流终点, 使整个配送成本最低(由小车的行驶距离决定)和物流任务等待配送时间最短. 调度优化建模时做如下假设:

(1) 当小车被指派多个物流任务时, 小车完成一个任务后直接执行下一个任务.

(2) 车间中各站点之间的距离已知.

(3) 一个小车在同一时刻只能承担一个物流任务.

(4) 小车一次只能运输一个载具的物料.

(5) 一个载具只能装载一个工位的物料.

(6) AGV行驶速度恒定, 其配送成本只和运行距离有关.

1.2 数学建模

为了贴近生产物流实际情况, 模型参数变量定义如表1所示.

1.2.1 物流任务计算

由于一个工位加工任务对应多个工件, 根据物流能力需要转换为 ${j_k}$ 个物流任务. 式(1)是所有加工工位所需原材料载具的计算公式, $\displaystyle\sum\limits_m {\displaystyle\sum\limits_y {{w_{kmy}}} } $ 是计算工位 $k$ 需要的所有原材料数, 然后根据物料载具关系, 计算出该工位需要的原材料载具数 ${j_k}$ . 小车每次运输一个载具, 一个载具是一个物流任务. 式(2)为待运输的物流任务集合, 是需要转运的原材料和实时呼叫的物流任务的集合.

$ J = {\left( {{j_k} = \displaystyle\sum\limits_u {\frac{{\displaystyle\sum\limits_m {\displaystyle\sum\limits_y {{w_{kmy}}} } }}{{{n_{uy}}}}} } \right),\;\;k \in 1, \cdots ,n} $

(1)

$ {{X}} = H \cup J $

(2)

1.2.2 目标函数

为了实现制造车间生产效率的最大化, 并更好地控制配送成本. 车间物流调度需要满足以下要求: ① 原材料按时配送, 使原材料的到达时间和需求时间之差最小. ② 实时呼叫的物流任务及时配送, 使物流任务等待运输时间最小. ③ 运载小车的利用率高, 即运载小车行驶最少的路程满足物流配送的需求. 基于此, 本文的目标函数由两部分组成, 分别是最小化时间惩罚成本和最小化运载小车的总行驶距离.

(1) 时间惩罚成本

为避免加工设备出现停机等待物料这种情况, 通常要求物料的运输时间早于或等于最迟运输时间. 若物流任务的开始运输时间早于或等于最迟运输时间, 则满意度最高, 惩罚值为0. 若物流任务的开始运输时间迟于最迟运输时间, 则用延迟的时间和优先级的平方相乘, 得到时间惩罚成本. 因为, 优先级高的物流任务相较于优先级低的在实际生产中会带来更大的损失. 设小车运行速度为15 m/min, 根据该速度计算物流任务的运输时间.

$ \min f1 = \sum\limits_p {(e{t_p} - s{t_p}) \times a_p^2},\; \;\;\forall p \in X $

(3)

(2) 运载小车的总行驶距离

小车的总行驶距离由运输物流任务的距离和完成上一个物流任务再去运输下一个物流任务所需的距离所组成.

$ \min f2=\sum\limits_{i}{\sum\limits_{p=1,q=2}{{{s}_{ipq}}+\sum\limits_{i}{\sum\limits_{p}{{{b}_{ip}},\;\;\forall i\in I,\forall p,q\in X}}}} $

(4)

1.2.3 约束条件

根据物流调度优化的实际需求, 设定如下约束条件:

(1) 任意时刻小车使用数量不超过小车总数量.

$ {\rm{ }}\sum\limits_i {{r_{id}} \le I,\;\;\forall i \in I,\forall d \in D} $

(5)

(2) 每个工位的出料位和进料位容量大于等于1.

$ {\rm{ }}\sum\limits_k {{c_{ik}} + } {c_{ok}} \ge 1,\;\;\forall k \in K $

(6)

(3) 载具装载的物料不大于载具的容量.

$ \sum\limits_m {\sum\limits_y {{w_{kmy}}} \times \frac{1}{{{n_{uy}}}} \le 1,\;\;\forall k \in K,\forall m \in M,\forall u \in U} $

(7)

(4) 进料位容量限制, 工位进料位的实时存储物料不超过其最大存储量限制.

$ c{i_{kd}} \le c{i_k} $

(8)

2 求解算法设计

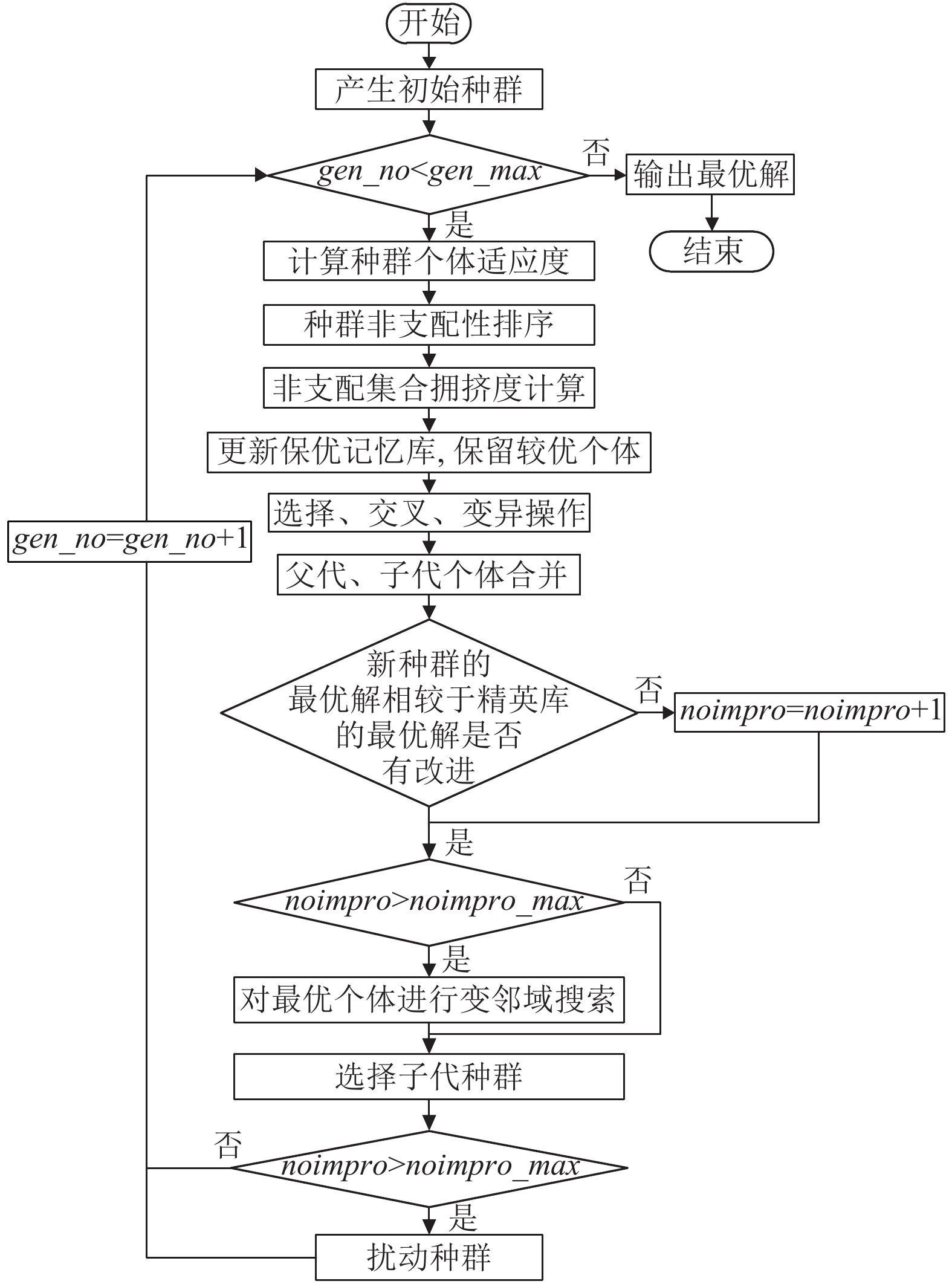
针对制造车间物流调度问题, 设计的混合变邻域搜索的改进遗传算法伪代码如算法1所示, 算法流程图如图1所示.

2.1 编码设计

常见的染色体编码方式有二进制编码、自然数编码、矩阵编码和交叉编码等. 由于本文研究问题为运输小车任务的指派, 以及运输小车任务的排序, 因此采用自然数编码和交叉编码相结合的方式. 染色体基因总数为偶数, 奇数位为小车编号, 偶数位为待运输的物流任务, 每两个基因组成一个基因片段, 每个基因片段表示小车i负责物流任务p的运输. 例如: 待运输的物流任务编号为{2, 9, 3, 5, 7, 8}, 可供使用的AGV小车编号为{1, 2}, 则一个可能的染色体为: {2, 2, 1, 9, 1, 3, 2, 5, 1, 7, 2, 8}. 表示2, 9, 3, 5, 7, 8物流任务分别由2, 1, 1, 2, 1, 2运输. 即小车1按顺序运输载具9, 3, 7, 小车2按顺序运输载具2, 5, 8, 如图2所示.

2.2 解码方法和适应度函数设计

按照2.1节编码设计规则对种群中每个染色体进行解码, 解码时根据物流任务编号找到其在车间所处对应的位置、优先级等相关信息.

以小车的总行驶距离、时间惩罚成本为优化目标建立的目标函数. 本文所优化问题为最小问题, 根据遗传算法原理, 适应度函数值越高的个体越容易存活, 在迭代过程中适应度函数值低的染色体会被淘汰, 适应度函数值高的染色体被保留, 因此, 经过多次迭代, 染色体质量会越来越好. 因此, 适应度值采取目标函数值的倒数, 即目标函数值越小, 适应度值越大, 适应度函数与目标函数的关系表达式如式(9)所示:

$ fi{t_i} = \frac{1}{{Y{}_i}},\;\;i = 1,2, \cdots,pop\_si{\textit{z}}e $

(9)

式中, $fi{t_i}$ 表示群体中第i个体的适应度值, ${Y_i}$ 表示第i个体的目标函数值, $pop\_si{\textit{z}}e$ 表示种群规模数.

算法 1. 混合变邻域搜索的改进遗传算法

输入: AGV小车信息 $\scriptstyle agv$ , 待运输物流任务信息 $\scriptstyle x$ , 车间中任意两个位置之间的距离 $\scriptstyle distance$ .

输出: 每个AGV小车运输的物流任务及顺序 $\scriptstyle solution$ .

参数: $\scriptstyle agv\_speed$ 为小车行驶速度.

变量: $\scriptstyle gen\_no$ 初始为0.

函数: 种群初始化 $\scriptstyle initiali{\textit{z}}ation()$ , 适应度值1 $\scriptstyle function1()$ , 适应度值2 $\scriptstyle function2()$ , 种群非支配排序 $\scriptstyle fast\_sort()$ , 拥挤度计算 $\scriptstyle crowding\_polution()$ , 精英个体保留 $\scriptstyle save\_elite()$ , 选择操作 $\scriptstyle bi\_cham()$ , 交叉操作 $\scriptstyle cross\_over()$ , 变异操作 $\scriptstyle mutation()$ , 两个染色体优劣比较 $\scriptstyle compare\_two\_gen()$ , 变邻域搜索 $\scriptstyle \operatorname{var} \_nei\_sear()$ , $\scriptstyle select\_chil()$ 选择子代个体.

$\scriptstyle solution$ = $\scriptstyle initiali{\textit{z}}ation(agv,{\rm{ }}x,{\rm{ }}pop\_si{\textit{z}}e)$ //产生初始种群

while   $\scriptstyle gen\_no$ < $\scriptstyle max\_gen$ do

    for $\scriptstyle i = 0$ to $\scriptstyle pop\_si{\textit{z}}e$

         $\scriptstyle {f_{\rm{1}}}$ $\scriptstyle \leftarrow $ $\scriptstyle function1(solutio{n_i},{\rm{ }}x,{\rm{ }}distance,{\rm{ }}agv\_speed)$ //计算种群个体适应度值1

         $\scriptstyle {f_{\rm{2}}}$ $\scriptstyle \leftarrow $ $\scriptstyle function2(solutio{n_i},{\rm{ }}x,{\rm{ }}agv)$ //计算种群个体适应度值2

    end for

     $\scriptstyle non\_dominated\_sort$ = $\scriptstyle fast\_sort({f_1},{\rm{ }}{f_2})$ //种群之间进行快速非支配性排序, 得到非支配性排序集合

    for $\scriptstyle j$ in $\scriptstyle non\_dominated\_sort$ do

         $\scriptstyle crowd\_distance$ $\scriptstyle \leftarrow $ $\scriptstyle crowding\_polution({f_1},{\rm{ }}{f_2},{\rm{ }}non\_dominated\_sor{t_j})$ //计算非支配集合中每个个体的拥挤度

    end for

     $\scriptstyle elite\_indivi = save\_elite(elite\_si{\textit{z}}e)$ //保留精英个体

     $\scriptstyle selected\_solutioin = bi\_cham(solution)$ //选择操作

    for $\scriptstyle selected\_solutioin$ 的每两个元素 do

         $\scriptstyle cross\_solution$ $\scriptstyle \leftarrow $ $\scriptstyle cross\_over(solutio{n_1},{\rm{ }}solutio{n_2})$ //交叉操作

    end for

    for $\scriptstyle n$ in $\scriptstyle cross\_solution$ do

         $\scriptstyle mutation\_solution$ $\scriptstyle \leftarrow $ $\scriptstyle mutation(cross\_solutio{n_i})$ //变异操作

    end for

     $\scriptstyle solution$ $\scriptstyle \leftarrow $ $\scriptstyle mutation\_solution$ //父代、子代个体合并

    if not $\scriptstyle compare\_two\_gen(solutio{n_0},{\rm{ }}elite\_indiv{i_0})$ then //新种群的最优解相较于精英库的最优解是否有改进

         $\scriptstyle noimpro + = 1$

    end if

    if $\scriptstyle noimpro > noimpro\_\max $ then //种群最优解已有 $\scriptstyle noimpro\_\max $ 代没有改进

             $\scriptstyle \operatorname{var} \_nei\_sear(solutio{n_0})$ //对最优个体执行变邻域搜索

    end if

     $\scriptstyle solution = select\_chil(solution,{\rm{ }}elite\_indivi)$ //通过帕累托等级和拥挤距离选择子代种群

    if $\scriptstyle noimpro > noimpro\_\max $ then //种群最优解已有 $\scriptstyle noimpro\_\max $ 代没有改进

　 $\scriptstyle solution = solution[0,pop\_si{\textit{z}}e/2]$ + $\scriptstyle initiali{\textit{z}}ation(agv,{\rm{ }}x{\rm{, }}pop\_si{\textit{z}}e/2)$

//对种群进行扰动, 保证迭代过程中个体的多样性, 生成大小为 $\scriptstyle 1/2\times (pop\_si{\textit{z} }e)$ 的个体替换子代适应度较低的个体

    end if

     $\scriptstyle gen\_no{\rm{ }} + = {\rm{ }}1$

end while

循环最优解 $\scriptstyle solutio{n_0}$ , 得到每个小车的物流任务及顺序

2.3 初始种群的生成

初始种群以物流任务优先级从高至低排序和随机生成相结合的方式生成.

以随机生成方式产生初始种群的具体步骤如下:

步骤 1.  根据可调用的小车编号, 确定小车的集合I.

步骤 2.  用生成随机数的方法从指定集合I中对染色体的每个基因产生随机数 ${x_i} \in I$ , 染色体基因个数等于待运输物流任务数X.

步骤 3.  在生成的染色体每一位基因后面随机插入一位新的基因, 表示物流任务编号, 染色体长度扩展为2P, 染色体扩展方法如图3所示.

步骤 4.  重复以上步骤, 产生大小为 $pop\_si{\textit{z}}e$ 的初始种群.

以物流任务优先级从高至低排序产生初始种群的具体步骤如下:

步骤 1. 将所有物流任务按照优先级进行降序排序(优先级最高为4).

步骤 2. 随机打乱小车编号的顺序.

步骤 3.  循环小车编号列表和物流任务编号列表, 当循环至最后一个小车编号时, 改变索引至第一个小车, 直至遍历完所有的物流任务, 每一次取出小车编号和物流任务编号, 小车编号后面跟着物流任务编号.

步骤 4.  染色体的大小为2倍物流任务长度. 重复执行上述操作 $pop\_si{\textit{z}}e$ 遍, 生成规模为 $pop\_si{\textit{z}}e$ 的初始种群.

2.4 交叉算子

选择操作采用二元锦标赛选择的方法按照概率选择适应度值较高的染色体参与遗传操作. 为了产生不同小车物流任务的分配方案, 通过交叉操作来增大物流任务分配解空间的搜索范围. 首先从种群中选出两个染色体, 对于偶数位, 将染色体的某一个位置切断, 将交叉位置前的染色体片段加到对方染色体个体前面, 并删除对方染色体中偶数位与交叉位置前染色体片段偶数位相同的值及对应前一位的奇数位. 对奇数位, 为每个奇数位生成一个随机数, 根据随机数的大小决定哪个父染色体贡献哪些奇数位的基因, 即随机数大的贡献给子染色体1, 随机数小的贡献给子染色体2, 如图4所示.

2.5 变异算子

为了维持种群的多样性以防止算法过早收敛, 采用变异操作提高算法的局部搜索能力. 传统的变异算子是选择若干个基因位, 然后随机修改基因的值, 变异后会出现非法解. 本文采用改进的变异算子, 如图5所示. 改进的变异算子是对偶数位进行变异操作, 获取染色体奇数位的基因值, 记为 $a$ , 寻找基因值与 $a$ 相等的奇数位基因, 将该奇数位基因后一位与变异基因交换, 并将已变异的基因标记, 以不再进行第二次变异. 这一操作是改变同一个小车执行物流任务的顺序.

2.6 精英保留策略

传统遗传算法中交叉、变异算子的作用个体均来自于子代种群, 该方法有一个明显缺点: 种群进化中优秀的个体得不到保护以致在下一轮迭代中易破坏. 因此, 通过使用保优记忆库更新策略来解决这一问题, 在每一代迭代结束后, 将保优记忆库中的精英个体合并到当代得到的新种群中, 合并的规则是若保优记忆库中的解和新种群的解两个目标函数均相同, 则只选择一个. 然后通过精英选择策略选择规模为 $elite\_si{\textit{z}}e$ 的个体加入库中进行保护, 精英选择策略是首先进行帕累托分层得到每个个体的帕累托等级并计算每层个体之间的拥挤距离, 优先选择帕累托等级低的个体, 若多个个体帕累托等级相同, 则选择拥挤距离较大的个体.

2.7 变邻域搜索算法

由于遗传算法求解过程中容易陷入局部最优解, 因此采用变邻域搜索策略来解决这一问题. 其思想是首先从最小邻域开始搜索解空间得到一个局部最优解. 然后通过系统地改变邻域结构, 基于该局部最优解, 重新从最小邻域开始搜索得到下一个局部最优解. 变邻域搜索算法是基于邻域结构集而非单一邻域结构, 因此, 比固定邻域结构的算法搜索能力更强. 变邻域搜索算法伪代码如算法2所示, 流程如图6所示.

针对本文模型特点, 设计6个随机邻域结构搜索机制, 具体如下:

(1) 3种同一小车内搜索策略, 即通过一定的规则改变同一个小车运输物流任务的顺序.

① swap算子

任意交换同一个小车的物流任务, 对同一个小车, 随机选取两个节点, 交换两个节点. 如图7(a)所示.

算法 2. 变邻域搜索算法

输入: 初始解ori_gen

输出: 变邻域搜索后的解 $\scriptstyle vns\_gen$

变量: $\scriptstyle k,\;m$ ,初始值为1

函数: 比较新解和初始解的目标函是否相等 $\scriptstyle compare()$

while   $\scriptstyle k \le k\_\max$ do

       $\scriptstyle vns\_gen = select\_vns(ori\_gen,{\rm{ }}m)$ //按照邻域结构 $\scriptstyle {V_m}$ 对解 $\scriptstyle ori\_gen$ 进行变邻域搜索, 随机产生新解 $\scriptstyle vns\_gen$

      if $\scriptstyle compare(ori\_gen,vns\_gen)$ //若 $\scriptstyle ori\_gen$ 的目标函数1和目标函数2均小于 $\scriptstyle vns\_gen$

           $\scriptstyle ori\_gen = vns\_gen$ //替换解

           $\scriptstyle m = 1$ //基于当前局部最优解重新从最小邻域开始搜索找到下一局部最优解

      else

          if $\scriptstyle m < m\_\max $ //若 $\scriptstyle m$ 未达到最大邻域结构数

                 $\scriptstyle m{\rm{ }} + = {\rm{ }}1$

          else

                  $\scriptstyle m = 1$

          end if

      end if

end while

② 2-opt算子

对某一个小车, 随机选取两个不相邻的节点, 然后翻转两个节点之间的节点, 得到新染色体, 如图7(b)所示.

③ or-opt算子

将同一个小车相邻的两个物流任务一起移动到其他位置. 即随机选取同一个小车的两个相邻的位置, 随机选择该小车的一个物流任务作为一个插入节点, 并在移动后保持相邻, 如图7(c).

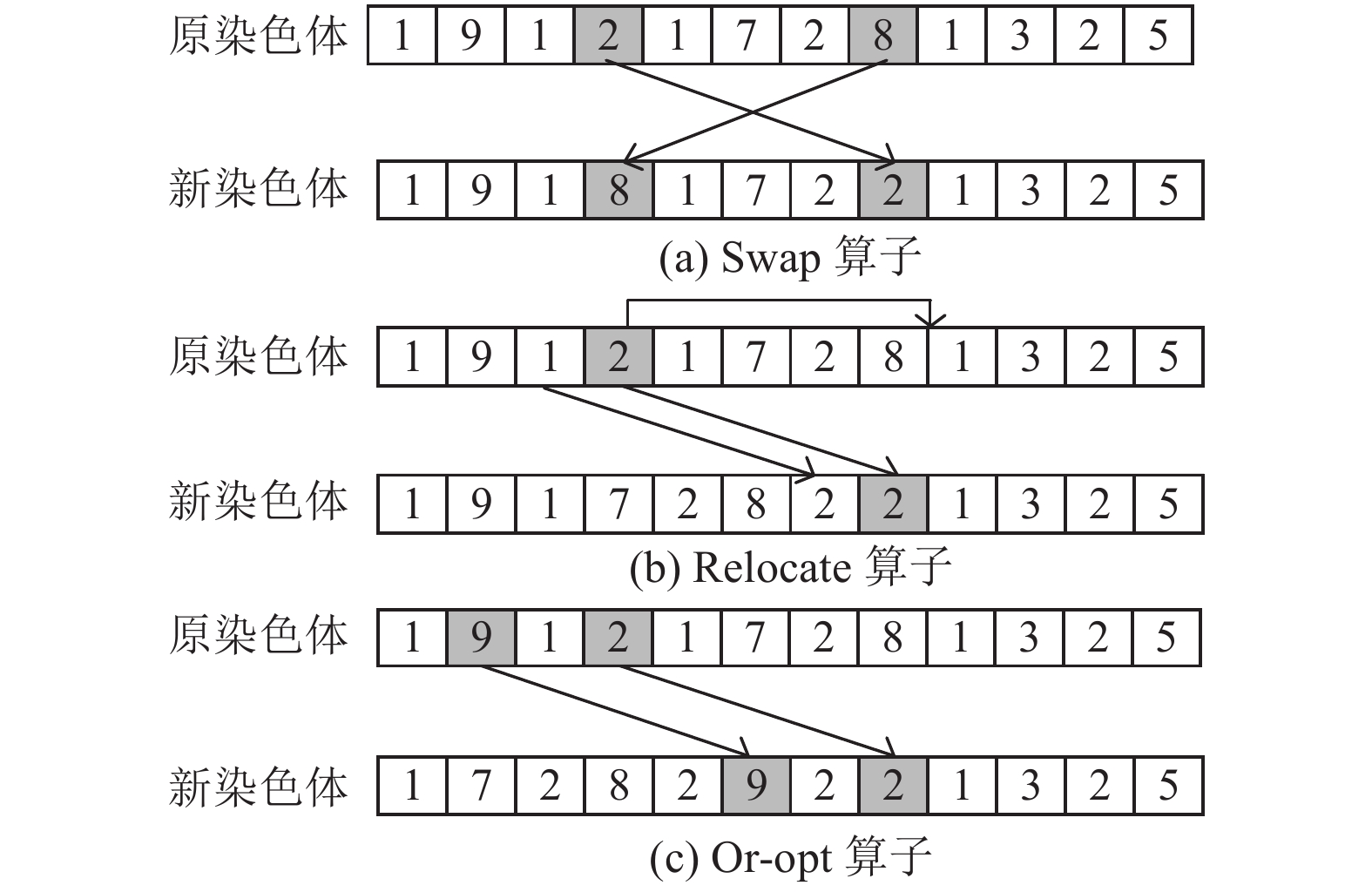
(2) 3种不同小车间搜索策略, 即通过一定的规则改变两个小车的物流任务.

① swap算子

随机选择两个小车, 在小车1和小车2分别随机选取两个小车的一个物流任务, 交换这两个节点, 如图8(a)所示.

② relocate算子

随机选取两个小车, 随机选取小车1的一个物流任务m, 随机选取小车2的一个物流任务n, 将小车1的物流任务m移动到小车2物流任务n后的位置, 如图8(b)所示.

③ or-opt算子

将其中一个小车的相邻两个物流任务移动到另一个小车, 如图8(c)所示.

为了进一步降低物流成本和提高工位满意度, 设计基于关键AGV小车的插入邻域、基于关键物流任务的交换邻域的调整策略, 具体如下:

(1) 基于关键AGV小车的插入邻域

将总行驶距离最大的AGV定义为关键AGV小车, 表示为 ${I_{\rm main}}$ , 最大距离记为L. 通过将 ${I_{\rm main}}$ 的物流任务分配给其它AGV, 可以均衡每辆AGV的任务量, 同时会降低运输所有物流任务的最大完成时间. 该邻域结构具体描述为: 遍历选择 ${I_{\rm main}}$ 中的物流任务插入到其它AGV的物流任务序列中, 若插入后L和两个目标函数值均降低了, 则接受该物流任务移动, 否则重新选择 ${I_{\rm main}}$ 中的物流任务插入序列, 直到选择 ${I_{\rm main}}$ 中的所有物流任务.

(2) 基于关键物流任务的交换邻域

将小车i运输完物流任务p再去运输物流任务q的空载行驶距离 ${s_{ipq}}$ 最大的物流任务定义为关键物流任务, 表示为 ${Q_{\rm main}}$ . 通过将 ${Q_{\rm main}}$ 和其它物流任务进行交换, 可降低AGV的空载行驶距离, 使AGV的利用率最大. 该邻域结构具体描述为: 将 ${Q_{\rm main}}$ 与其它物流任务依次交换, 若所有AGV的总空载距离和两个目标函数值均降低了, 则接受该物流任务的交换, 否则重新选择其它物流任务, 直到选择了所有的物流任务.

3 数值实验与分析 3.1 实验相关数据

(1) 案例设计

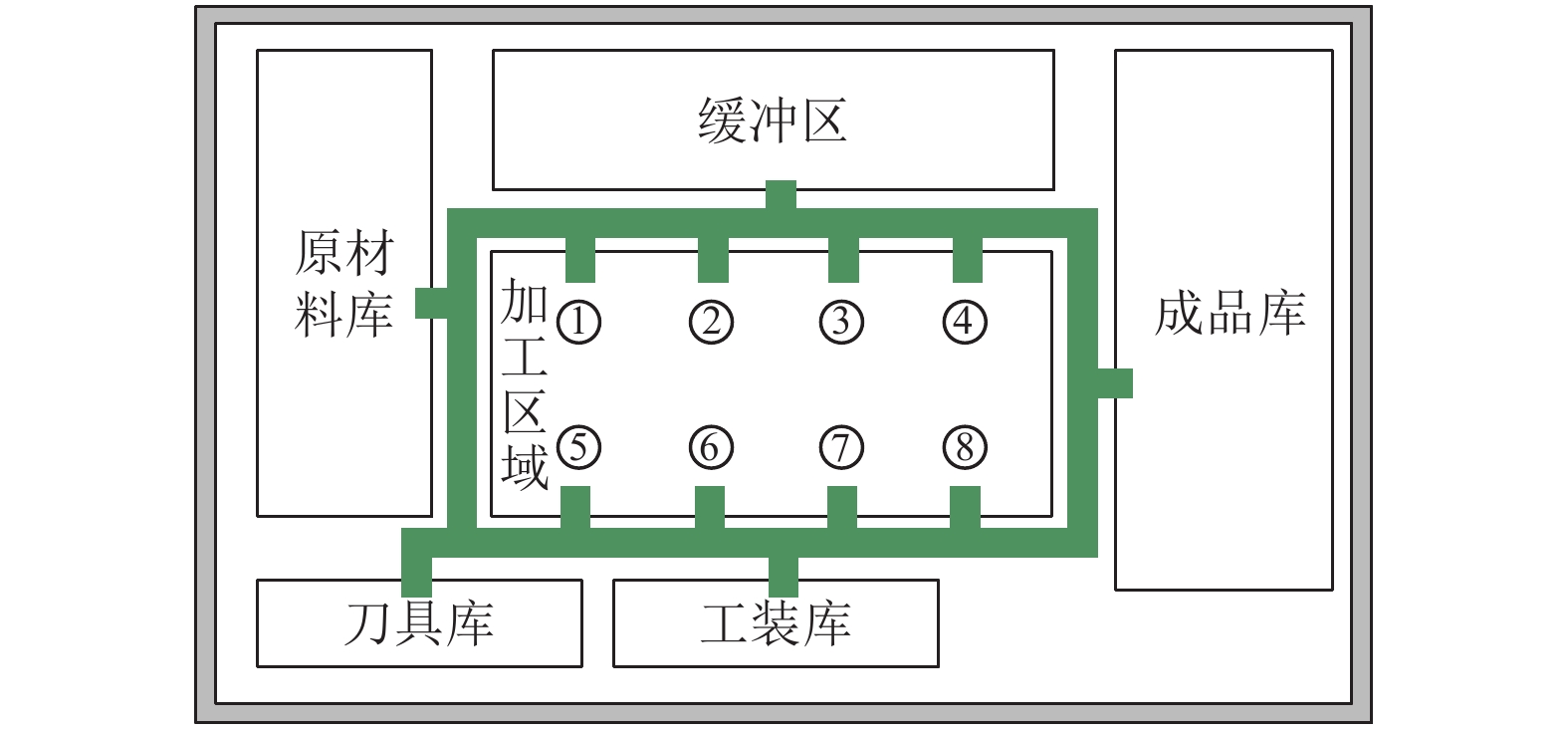
本文以某离散车间为例验证算法的有效性. 车间中任意两个位置之间的距离值如表2所示, 车间布局如图9所示, AGV小车的物流路径在图中已用实线标明, 每条路径同时可有两辆AGV小车通行, 其中共有8个加工工位、1个原材料库、1个缓冲区、1个成品库、1个刀具库和1个工装库, 在程序中依次从左向右转换为0至12的编号. 物流任务在车间中的流转均由AGV小车运输.

(2) 算法相关参数设置如表3所示.

(3) 物流任务的实时信息模型

为了更好地进行管理和数据交换, 模型的输入一共包含两部分. 第一部分是运载小车的信息, 分别是可调用小车编号和小车完成当前正在执行任务后的位置. 第二部分是待物流任务的信息, 每个物流任务的信息包括: 任务 $id$ 、任务起始位置、任务终止位置、任务优先级、任务最晚运输时间. X个任务的信息存储在矩阵X中, 如式(10)所示, 其中 $i{d_p}$ 表示物流任务的编号, ${f_p}$ 表示物流任务的起始位置, ${e_p}$ 表示物流任务的终止位置, ${a_p}$ 表示任务的优先级, $s{t_p}$ 表示任务的最晚运输时间.

$X = \left[ {\begin{array}{*{20}{c}} {i{d_1}}&{{f_1}}&{{e_1}}&{{a_1}}&{s{t_1}} \\ {i{d_2}}&{{f_2}}&{{e_2}}&{{a_2}}&{s{t_2}} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {i{d_p}}&{{f_p}}&{{e_p}}&{{a_p}}&{s{t_p}} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {i{d_x}}&{{f_x}}&{{e_x}}&{{a_x}}&{s{t_x}} \end{array}} \right]$

(10)

在优先级的定义中, 1 代表“普通任务”, 2 代表“重要任务”, 3代表“紧急任务”, 4代表“更紧急任务”.

为了验证本文模型和算法的有效性, 随机构造一个实验案例, 如表4和表5. 最晚运输时间在区间[0, 60]中随机产生.

3.2 实验结果分析

与单目标优化算法不同, 多目标优化结果通常不是单个最优解, 而是一个Pareto最优解集. 根据本文车间物流调度需求, 算法需要确定每个AGV小车运输的物流任务, 及运输每个物流任务的顺序. 本文是从最优解集中根据两个目标函数的和选取最优解.

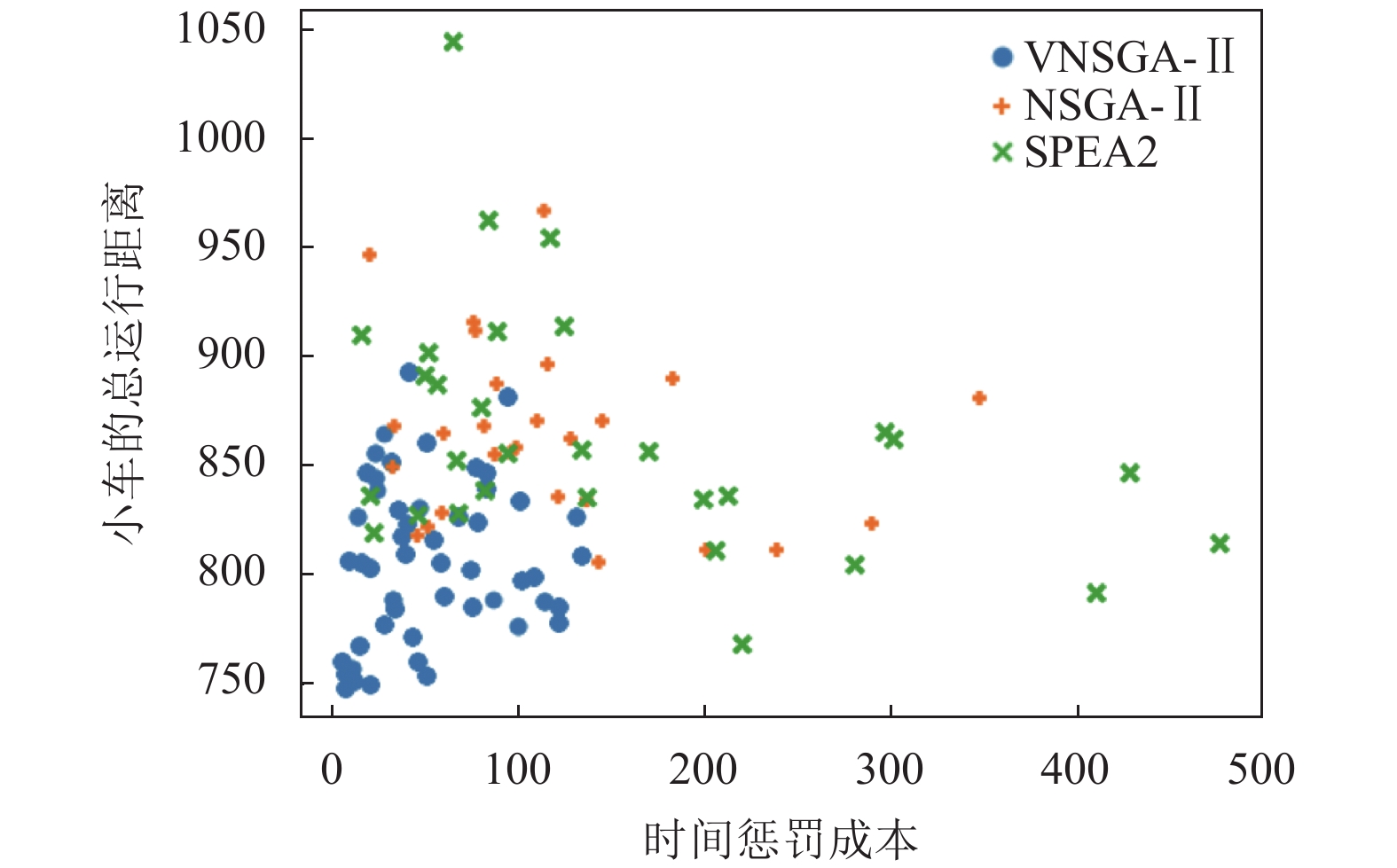
为了验证本文设计的VNSGA-II算法求解的有效性, 在本文设计的案例条件下与两种经典的多目标优化算法NSGA-II, SPEA2的优化结果进行实验分析. 3种算法实验条件及参数相同, 采用Python语言完成上述算法的编程, 3种算法分别运行20次, 生成的Pareto最优解集如图10所示, 算法优化结果分析如表6和表7所示, 其中在表6中 ${f_1}$ 和 ${f_2}$ 分别表示时间惩罚成本和运载小车的总行驶距离.

由表6可知, VNSGA-II的优化结果在两个目标函数: 时间惩罚成本和运载小车的总行驶距离上在最优解和平均解上均优于NSGA-II和SPEA2. 因本文研究的问题是最小问题, 即两个目标函数值越小越好, 由图10可以看出, 本文设计的VNSGA-II算法得到的Pareto最优解更多, 在解的质量上总体比NSGA-II和SPEA2更好. 表7是3个算法运行的最优解AGV的物流任务分配情况及转运顺序和每个行驶小车的总空载距离. 因此, 从以上实验可以看出本文设计的算法在保持运输物流任务延迟时间较低的情况下, 有效降低了运载小车的总行驶距离和空载距离, 既缩短了物流任务的搬运时间又节省了车间的物流成本.

4 结束语

本文以制造车间物流调度为实际背景, 建立多目标优化模型, 针对该问题设计了求解多目标的VNSGA-II算法, 该算法包含遗传算法的基本操作, 并对最优解集进行变邻域搜索. 通过实验, 结果表明:

(1) 模型考虑物流任务的时间惩罚成本和AGV小车的总行驶距离两个方面, 有效地平衡了车间的生产效率和车间的生产成本, 具有较强的实用性.

(2) 与两种多目标经典优化算法NSGA-II和SPEA2的实验结果对比表明, VNSGA-II算法在求解质量上均优于NSGA-II和SPEA2.