2. 贵州大学 公共大数据国家重点实验室, 贵阳 550025;
3. 贵州大学 密码学与数据安全研究所, 贵阳 550025
2. State Key Laboratory of Public Big Data, Guizhou University, Guiyang 550025, China;
3. Institute of Cryptography and Data Security, Guizhou University, Guiyang 550025, China
信任作为一个抽象的概念, 却在不同领域之中都显得十分重要[1], 在职场领域有调查指出, 职场失信的重灾区集中在招聘环节, 个人履历造假情况超过了半数以上. 在传统的履历存证方法中, 通常需要委托第三方机构进行候选人背景调查, 然后再由第三方机构出具相关的调查报告, 比如A企业需要核实候选人B的履历信息, 就需要第三方机构在收到委托与授权后充当中心角色向C企业进行核实并返回调查报告[2]. 此过程涉及到多方的参与, 且对于最终履历数据的管理呈现为以第三方机构为核心的中心化结构, 这对候选人的履历信息管理、真实性鉴别带来了十分巨大的困难. 同时, 随着云计算技术的崛起, 使用云存储技术进行数据存储是大势所趋, 而云服务器通常被认为是半诚实且好奇的[3], 这意味着它将诚实地执行算法,但会尝试学习尽可能多的私有信息. 因此, 如何安全的将真实可靠的履历数据存放在云服务器中, 如何安全正确的将履历数据进行共享, 仍旧是一个不小的难题. 区块链[4]作为一种去中心化的存储结构, 存储在链上的数据具有不可篡改、公开透明、可溯源性等特征, 这些特性天然的适合需要保证数据可信度以及公开透明的应用场景, 因此基于区块链网络进行信息共享是解决传统信息共享中心化的途径. 目前基于区块链技术对人才履历存证的相关研究较匮乏, 但在其他方面比如数字版权存证[5]、金融行业[6,7]、电子病历共享[8]等方面均取得了巨大的进展. 上述研究与区块链技术在人才履历存证中的应用需要考虑的因素基本相同, 即如何保证数据的真实性与安全性、如何保证用户收到数据的正确性.
Song等人[9]为了节省本地存储空间与保护数据安全, 首次提出了一种基于单关键字的可搜索加密(Searchable Encryption, SE)方案, 方案将所有文件加密后上传到服务器进行存储, 在需要对文件进行检索时使用加密后的关键字与所存储文件进行一一比较, 以发现是否存在所需文件, 但在数据较大时会限制检索的效率. 基于此项研究, Cao等人[10]首次提出了基于多关键字的SE方案, 方案引入“坐标匹配”相似性度量以提升搜索效率并且实现在不同威胁模型下的系统安全性. Sun等人[11]最早开始研究有效搜索结果验证问题, 并提出了相应的可验证SE方案, 他们的方案使得用户能够进行安全的联合关键词搜索, 更新外包文件集并有效地验证搜索结果的真实性. Naveed等人[12]提出了动态SE方案, 方案允许用户使用服务器存储加密文档的动态集合, 然后在对这些加密文档进行快速搜索的同时, 向服务器显示最少的信息. Chen等人[8]基于区块链提出了一种可验证最终结果的SE数据共享方案, 方案基于布尔表达式对链上数据进行搜索, 相比文献[9]方案提升了文件搜索效率, 但一旦第三方获取了数据索引的内容可能会导致数据的泄露. Hu等人[13]结合区块链技术首次提出了无需验证最终结果正确性的SE数据共享方案, 方案引入押金机制, 确保了数据共享过程中的参与方在无需验证结果的情况下收到正确的执行结果, 实现了参与者之间的公平性与隐私保护.
本文结合区块链与可搜索加密技术提出了一种基于区块链的可搜索加密人才履历共享方案, 去除传统第三方机构, 解决了传统人才履历存证中数据管理中心化、履历造假等问题. 所提方案首先基于区块链不可篡改的特性, 结合云存储技术对履历数据实现链上链下协同存储, 保证了履历数据的真实性. 其次, 在履历数据共享过程中, 利用区块链去中心化的特性取代传统第三方机构, 结合可搜索加密技术实现了参与方之间的公平性与数据存储、更新时的隐私保护. 最后基于Hyperledger[14]联盟链实现方案并对安全性和性能进行分析, 保证方案的正确性以及实际的可行性.
2 相关技术 2.1 联盟链区块链技术发展至今, 演化出了许多分支. 按照网络结构去中心化程度的不同可以分为:
公有链: 全网公开, 无用户授权机制的区块链, 节点可以自由出入网络, 以文献[4]为代表;
联盟链: 允许授权的节点加入网络, 可根据权限查看信息, 往往被用于机构间的区块链, 也称为行业链, 代表有文献[14];
私有链: 所有网络中的节点都掌握在单独的个人或实体手中, 链上的数据不被其他任何人所知晓.
由于访问联盟链需要许可的特性, 现在已被广泛应用于银行、保险、证券、商业协会等[15]. 联盟链的记账节点是提前在内部预选的多个节点作为记账节点, 新块的产生由预选记账节点决定, 其他节点只参与交易过程, 但不过问记账细节, 因此联盟链不需要通过工作量证明算法(Proof Of Work, POW)共识, 转而更倾向于实用拜占庭算法(Practical Byzantine Fault Tolerance, PBFT)或委托权益证明(Delegated Proof Of Stake, DPOS)[16]共识算法来保证数据的正确性. 由于共识机制的更改, 联盟链通常还具有更高的系统吞吐量, 更低的资源消耗, 还允许拥有权限的第三方通过开放的API查询指定的数据, 这些特性极大拓宽了区块链的应用领域.
2.2 智能合约智能合约[17]定义为“一套以数字形式定义的承诺, 包括合约参与方可以在上面执行这些承诺的协议”. 在比特币以前, 智能合约由于缺少可信的运行环境, 并没有在实际生产中实现和运用. 但是在区块链系统中, 智能合约在共识和网络的封装之上, 可在不涉及第三方的情况下促进交易的可靠执行, 并且所有交易都是可追踪且不可逆的, 隐藏了区块链网络中各节点的复杂行为, 同时提供了区块链应用层的接口. 这意味着智能合约可提供优于传统合约法的安全性, 并降低与合约相关的交易成本, 这些特性与区块链的结合同样增加了区块链的应用场景.
2.3 可搜索加密可搜索加密问题最早源于文献[9]: 假设用户试图将文件存放在诚实但好奇的服务器中, 以节约本地资源, 同时为保护文件隐私, 须采用某种加密方式将文件加密后存储. 可搜索加密主要由4个算法组成[18]:
(1)加密: 用户使用密钥对明文进行加密并将所得密文上传服务器.
(2)陷门生成: 用户使用密钥生成待查询关键词的陷门, 要求陷门不能泄露关键词的任何信息.
(3)检索: 服务器以陷门为输入, 执行检索算法, 返回所有包含该陷门对应关键词的密文文件, 要求服务器除了能知道密文文件是否包含某个特定关键词外, 无法获得更多信息.
(4)解密: 用户使用密钥解密服务器返回的密文文件, 获得明文结果.
从密码构造角度可搜索加密现可划分为两大类, 即对称可搜索加密与非对称可搜索加密. 其中, 对称可搜索加密的构造通常基于伪随机函数, 具有计算开销小、算法简单、速度快的特点, 除了加解密过程采用相同的密钥外, 其陷门生成也需密钥的参与. 相比于非对称加密, 对称加密的计算量小, 加密速度快, 当加密大量数据时其实现效率要比非对称加密高6–10倍, 但密钥的分发缺乏安全, 算法的安全性在很大程度上依赖于密钥[19]. 非对称可搜索加密使用两种密钥: 公钥用于明文信息的加密和目标密文的检索, 私钥用于解密密文信息和生成关键词陷门. 非对称加密算法通常较为复杂, 加解密速度较慢, 然而其公私钥相互分离的特点, 避免了在发送者与接收者之间建立安全通道: 发送者使用接收者的公钥加密文件和关键词, 检索时, 接收者使用私钥生成待检索关键词陷门, 服务器根据陷门执行检索算法后返回目标密文, 具有较高的实用性.
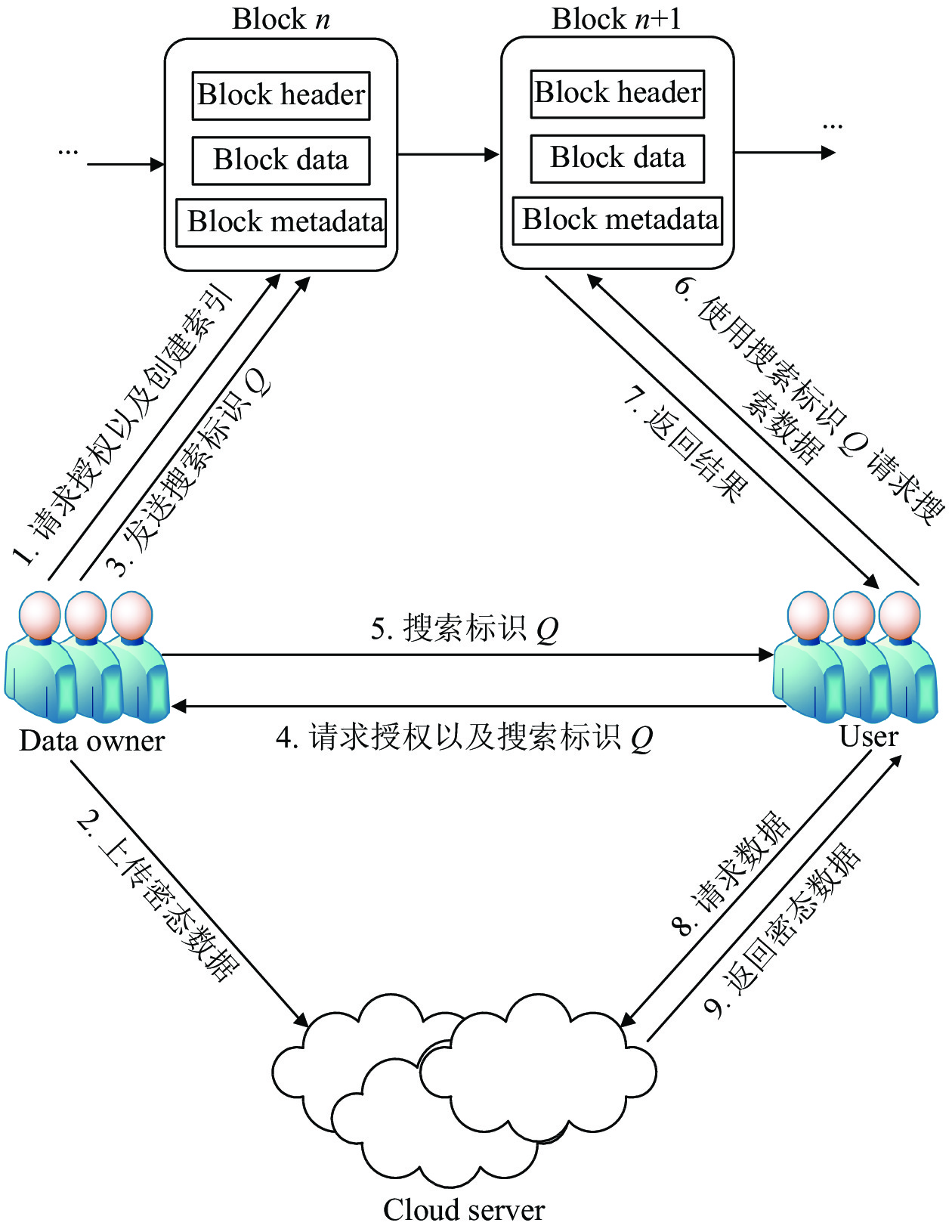
3 系统模型通过对传统人才履历存证流程的分析, 本文提出了一个基于区块链的可搜索加密人才履历共享方案, 方案模型如图1所示.
|
图 1 系统模型 |
模型共包含4个实体, 分别是数据拥有者、用户、云服务器以及区块链, 表示为四元组(Cs,B,D,U). 其中Cs代表云服务器; B代表区块链网络; D代表数据拥有者集合, 由负责生成人才履历信息并将数据上链的用户组成, 即:
| $ D = \left\{ {{D_1},{D_2}, \cdot \cdot \cdot ,{D_n}} \right\} $ | (1) |
U代表用户集合, 由需要从链上获取数据的参与方组成, 即:
| $U = \left\{ {{U_1},{U_2}, \cdot \cdot \cdot ,{U_n}} \right\}$ | (2) |
模型改进了传统履历存证完全依靠人工方式的缺点, 去除了传统履历存证中的第三方机构, 进而减少了履历造假的可能性. 并且模型对参与方进行了严格的身份权限控制: 数据拥有者需要通过身份认证才能获得区块链的准入权限, 而用户在对数据进行搜索之前同样需要获得数据拥有者授权以获得数据索引才能进行数据的搜索工作, 这样的设计从源头上解决了可能的数据造假问题, 相比传统的履历存证提升了效率与数据真实性. 完整的系统过程描述如下:
(1) 数据拥有者Di申请区块链准入权限以加入集合D, 之后Di对已有数据运行第4节中算法以获得加密后的密文C与数据索引I.
(2) 数据拥有者Di上传密文C至云服务器Cs.
(3) 数据拥有者Di上传索引I至区块链网络B.
(4) 用户Uj向Di申请授权以获得搜索标识Q.
(5) Di分别将搜索标识Q发往区块链B及用户Uj.
(6) Uj用标识Q向区块链网络B发起搜索请求.
(7) B执行搜索算法之后返回数据索引给Uj.
(8) Uj使用数据索引向云服务器请求密文Cm.
(9) 云服务器返回对应密文Cm给Uj.
在上述过程中, 搜索标识Q包含当次查询所需的数据索引信息以及双方的身份信息, 并且分别由数据拥有者以及用户发往区块链进行存储备份, 再由智能合约调用搜索算法对Q进行相关数据搜索, 并假设最终结果将通过一个安全的通道传输给用户.
4 方案设计在本节中, 将给出所提方案的具体构造. 方案基于区块链与可搜索加密技术, 不仅可以保证履历数据的真实性, 实现数据的隐私保护, 还具有公平性和健壮性. 方案一共由3个多项式时间算法组成: 初始化, 查询, 更新. 我们定义了如下两个伪随机函数, 其中λ是系统安全性参数, *代表长度可为任意值. 假设所有数据存放在非关系型数据库CouchDB中, 且涉及到的其他符号定义如表1所示.
| $F:{\left\{ {0,1} \right\}^\lambda } \times {\left\{ {0,1} \right\}^\lambda } \to {\left\{ {0,1} \right\}^\lambda }$ | (3) |
| $G:{\left\{ {0,1} \right\}^\lambda } \times {\left\{ {0,1} \right\}^\lambda } \to {\left\{ {0,1} \right\}^ * }$ | (4) |
| 表 1 符号定义 |
在初始化阶段, 数据拥有者首先将随机生成两个长度为λ的mk、sk以作为后续生成中间参数以及进行数据加密的密钥. 然后对于已有的每份数据, 将mk、sk以及整份数据作为算法的输入, 输出是数据的索引以及加密后的密文. 在对所有数据进行上述操作之后, 将输出的数据索引集合I发送到智能合约, 由智能合约进行索引的存储, 将输出的密文集合C存储至云端. 详细的算法步骤见算法1.
算法1. Setup
输入: mk, sk, R
输出: I, C
1. the data owner init list L
2. for r∈R
3. K1←F(mk, 1|| rid); K2←F(mk, 2||r)
4. g
5. add tuple (l, d||g)) to L
6. encrypt r with sk;
7. end for
8. the data owner send L to the smart contract
9. the smart contract init listγ, γD and γU
10. for tuple (l, d||g) ∈ L
11. add (l, d||g) to γ;
12. end for
13. end
在查询阶段, 用户首先向数据拥有者发送申请授权请求以获得特定数据的搜索标识Q. 数据拥有者先将Q发送至区块链进行记录, 然后再发送给用户. 用户在获得Q之后将其发往区块链进行数据查询, 由智能合约调用搜索算法执行当次数据搜索, 并判断搜索结果的有效性, 同时将Q再次记录到区块链中. 在所有操作执行完成之后由智能合约将数据索引返回给用户. 详细的算法步骤见算法2.
算法2. Search
输入: Q
输出: Dataindex
1. the data owner sends Q to the smart contract and the user;
2. the smart contract add Q to γD;
3. the user sends Q to the smart contract to get data index;
4. the smart contract:
5. add Q to γU;
6. l←F(K1, 1); d,g←Get(γ, l);
7. if d=⊥ && g=⊥
8. return false;
9. else
11. id←d⊕G(K2
10. return id;
11. end if
12. end
在更新阶段中包含了在新区块中新增履历数据和更新已有数据两个操作. 算法以mk、sk以及待操作的数据作为输入, 首先按照初始化阶段算法的思路对数据生成索引以及密文C, 然后再从操作集合O(新增add和更新update)中选取当次更新是做什么操作. 对所有数据进行上述操作之后, 将得到的索引以及密文集合分别发送至区块链以及文件存储系统, 再由智能合约根据每条数据对应的操作进行数据处理: 如果是新增操作, 则再插入一条数据, 否则就对已有数据进行更新操作. 详细的算法步骤见算法3.
算法3. Upgrade
输入: mk, sk, R
输出: I, C
1. the data owner init list LA;
2. for r∈R
3. K1←F(mk, 1|| rid); K2←F(mk, 2||r);
4. g
5. choose an operation o from list O;
6. add tuple (l, d, g, o) toLA;
7. encrypt r with sk;
8. end for
9. the data owner send LA to the smart contract;
10. the smart contract:
11. for tuple (l, d, g, o) ∈ LA
12. if o= add
13. add (l, d||g) to γ;
14. else
15. d', g'←Get(γ, l);
16. set d'=d, g'=g;
17. update γ with tuple (l, d'||g');
18. end if
19. end for
20. end
本文所提出的方案主要关注查询结果的准确性与公平性, 而没有考虑访问每条履历信息更细粒度的权限控制问题, 这可以使用现有的方案来实现, 例如使用ABE (Attribute-Based Encryption)算法来实现更细粒度的访问控制[20,21].
5 安全分析与实验仿真 5.1 安全分析上述方案通过引入区块链与可搜索加密技术以保证人才履历信息的真实性, 并且对于履历数据的存储与共享目标和文献[8,13]所提出的目标类似, 我们实现了履历数据在存储过程中的保密性、数据共享时的公正性和方案的健壮性.
真实性: 履历数据仅来自于上述模型中的数据拥有者, 由个人或企业直接向相应的验证方发起认证并获得履历数据. 由于在进行履历验证的各环节中均需要进行身份认证, 并且数据一旦生成就会在区块链中记录下来, 减少了全过程的参与方, 实现了履历数据存储的去中心化, 降低了履历造假的可能性, 提升了履历信息的真实性.
健全性: 显然在Hyperledger联盟区块链安全性保证的前提下, 本文所提方案实现了健全性. 因为智能合约代码直接由Hyperledger联盟区块链执行, 不受任何第三方的干扰, 同时区块链的共识机制可以确保每个操作的正确执行, 并且执行后的结果会被永久的存储在链上, 链上的所有节点都可以验证数据的有效性.
公平性: 在此前的多方参与数据共享方案中存在的问题是: 如何保证数据拥有者给出正确的数据索引, 以及如何确保用户无法抵赖称自己没有收到索引. 针对这两个问题, 在所提方案中, 当数据拥有者给出数据搜索标识Q时, 需先将其记录在链上集合γD中; 用户在进行数据搜索之前, 也需要将Q记录在链上集合γU中, 即:
| $D\xrightarrow{Q}{\gamma ^D},U\xrightarrow{Q}{\gamma ^U}$ | (5) |
当其中一方试图抵赖自己之前的操作时, 另一方可以选择发起请求验证交易并由智能合约执行以下算法判断撒谎者, 算法以验证交易作为输入, 首先判断请求者身份:
若交易发起者是数据拥有者, 判断集合γU中是否存在关于QD的数据, 若存在, 则返回1表示用户Uj撒谎, 否则返回null表示交易正常.
若交易发起者是用户, 则判断集合γD中是否存在关于QU的数据, 若存在, 与QU进行比较, 数据不一致则返回0表示Di撒谎, 否则返回null表示交易正常; 若不存在, 则返回0表示Di撒谎.
算法4. Sentence
输入: verify request
输出: 0|1|null
1. if requester ∈D
2. if find QD in γU
3. return 1
4. else
5. return null
6. end if
7. else
8. if find Qu in γD
9. if Qu≠Qu
10. return 0
11. else
12. return null
13. end if
14. else
15. return 0
16. end if
17. end
由于整个算法是由智能合约执行, 由系统的健壮性可知, 链上所记录的数据都是完全正确的, 因此无论是数据拥有者还是用户, 任何一方提供的错误信息都将被发现.
保密性: 为了证明方案的保密性, 我们使用一个在模拟者S和对手A之间的real-ideal模拟游戏来进行证明. 在此之前给出如下3个关于本文方案的状态泄露函数
给定初始化输入R, SL1
| $ S{L_1}\left( R \right) = \left( {\sum\nolimits_i^m {{R_i}} ,m} \right) $ | (6) |
同时它初始化一个空集合L, 一个密文集C, 并将他们进行存储.
给定一个搜索输入r, SL2被定义为:
| $ S{L_2}\left( r \right) = \left( {sp\left( {r,L} \right),Q} \right) $ | (7) |
其中, sp(r, L)表示搜索模式. 给定待搜索文档r, 它将输出搜索模式sp以及搜索标识Q.
给定一个更新输入(id, r), SL3被定义为:
| $ S{L_3}\left( {id,r} \right) = \left( {sp\left( {r,L} \right),ap\left( {i,d,L} \right),up\left( {i,d,L} \right)} \right) $ | (8) |
其中, ap(i, d, L)表示r关于L的新增模式; up(i, d, L)表示r关于L的更新模式.
定理1. 如果 F和G是伪随机的, 那么本文所提方案针对非自适应攻击是安全的.
证明: 我们假设S是多项式时间的模拟者, 那么对于任意同样是多项式时间的对手来说, 真实执行RealA(λ)的输出和模拟执行的IdealA, S(λ)的输出在计算上是难以区分的. 模拟器通过给定的泄漏函数SL模仿真实协议来模拟对手的视角. 例如, 为了模拟初始化阶段, S首先为每个搜索随机的选择k1, k2由搜索模式指定重复的次数. 对于所有的文件, S按真实的初始化阶段计算出l, d, g并将每一个键值对(l, d||g)加入到集合L中, 再随机的添加m个键值对到L中, 并最终创建出一个字典γ'. 类似的, S可以通过泄露函数SL模拟出搜索和更新请求. 因此, 由于F和G的伪随机性, 我们的定理成立. 特别的, 方案可以通过使用随机预言机以达到对自适应攻击的安全性[13,22].
5.2 实验仿真为了验证本文所提方法的安全性及性能, 我们使用了5台搭载Intel(R) Xeon(R) Gold 6278C CPU, 8 GB RAM, 操作系统为 CentOS 7.6的云服务器作为实验基础, 基于开源区块链网络Hyperledger Fabric 1.4.0, 构建了一个包含3个order节点, 4个peer节点, 使用CouchDB作为WorldState数据库, 智能合约由Java编写的区块链网络作为基础实验环境, 使用了搭载Intel core i5-7500 CPU,16 GB RAM, Windows10 (64 bit)的本地主机模拟数据拥有者以及用户进行所提方案的实验仿真, 同时忽略出块时间对实验结果的影响.
由于没有足够的履历信息数据集支撑, 因此本次实验选择了由Rajkovic等人[23]建立的Nursery数据集进行实验. 这是一个包含了12960条纯文本记录的数据集, 为了满足方案的条件, 我们为每条数据添加了文件id作为CouchDB数据库的_id字段, 并且将每条文本下含的8个属性进行调整以满足履历信息的数据格式. 实验共从3方面进行, 包含了系统的安全性、搜索以及数据更新的性能. 整个方案的初始化阶段可视作为更新操作的变体, 因此所需时间的多少可由初始化时具体的数据量估算, 此处没有进行实验.
针对方案的安全性, 我们设计了2组测试场景, 并分别对每种测试场景进行了系统安全性测试. 2组测试场景内容如下:
场景1. 未取得授权时数据拥有者以及用户对区块链的操作.
预期结果: 所有操作均被拒绝.
场景2. 取得区块链系统授权时数据拥有者以及用户抵赖的情况.
预期结果: 双方的抵赖操作均被发现.
通过对场景1和场景2各进行100次实验, 实验结果表明, 参与者在未取得授权的情况下, 在系统模型的健全性以及Hyperledger Fabric网络本身安全性的保证下, 所有的异常数据操作都被拒绝. 同时, 当取得授权的双方在对区块链做数据查询时, 在系统公平性的保证下, 如果是数据拥有者提供错误的数据索引给用户, 在出现异常时通过对链上存储的数据索引进行检验即可发现错误的数据索引项; 如果用户收到正确的数据索引却意图抵赖, 此时存在两种情况: 一是用户不进行数据查询操作, 那么即使他获得了数据索引也无法获得任何的原始数据信息. 二是用户进行数据查询, 除非使用正确的数据索引进行搜索, 否则仍旧无法获得任何信息, 而一旦使用正确的信息进行搜索, 此过程将被区块链系统记录下来, 即用户无法对此过程进行抵赖.
下面对本文所提方案的性能进行评估. 本文所提方案的时间开销主要分为两种类型: 搜索和更新操作的时间开销. 其中搜索的时间开销主要包含两部分, 即实际数据搜索时间以及将数据标识Q上链备份的时间, 如图2中曲线x所示, 当用户首次向服务器发起查询数据请求时, 由于用户需要与区块链网络之间建立连接, 因此需要花费更多的时间. 更新操作所需时间仅包含在新块中更新账本状态的时间, 因此整体消耗时间比数据搜索操作更低一些, 如图2中曲线y所示.

|
图 2 方案时间开销 |
根据上述实验表明, 本文提出的基于区块链的可搜索加密人才履历共享方案, 在数据搜索方面和文献[8,13]所提方案的搜索性能相比, 由于方案具备更加严格的搜索控制, 因而增加了部分开销. 但在数据更新方面, 由于本方案在数据更新时不需要做额外的状态判断, 因此数据更新性能要优于文献[13], 提升了对数据的更新效率.
下面将本文提出的方案与现有方案进行比较. 表2将从方案的查询模式、查询内容、是否支持对数据的动态更新等方面与其他方案进行对比.
Chen等人[8]提出的方案主要是针对电子病历共享. 方案采用范围查询对位于链上的病历数据进行搜索, 因而在数据量较少时拥有最快的搜索效率, 但是方案却不支持对数据的动态更新, 导致方案的通用性较差.
Hu等人[13]提出的信息共享方案支持对通用数据的信息共享. 方案对链上数据进行单关键字搜索, 因此在搜索文本的数量较多时搜索性能会趋近于一个稳定值; 同时方案还支持对数据的动态更新, 但是更新操作的开销远大于搜索操作开销, 并且在多方参与时需进行额外调整以满足多方之间的搜索公平性.
| 表 2 本方案与其他方案对比 |
本文提出的信息共享方案主要是针对履历信息进行共享, 方案通过对具体数据的搜索以实现查询特定履历数据的目的. 方案满足在履历数据发生变更时的数据动态更新操作, 并取缔了数据更新时在区块链上判断的过程, 提升了数据更新效率. 同时, 利用智能合约执行结果的正确性保证了在数据分享过程中双方之间的公平性与结果正确性.
6 总结本文基于区块链与可搜索加密技术对传统人才履历存证中存在的数据管理中心化、履历造假等问题提出了一个新的解决方案. 方案利用区块链取代传统第三方机构, 结合链上链下协同存储机制保证了履历数据的真实性, 并基于可搜索加密技术实现了参与方之间的公平性与数据存储、更新时的隐私保护. 通过对方案的安全性及性能进行分析与实验, 表明方案在支持人才履历共享的同时也满足隐私需求以及拥有足够的系统性能, 但同时对于恶意参与者的惩罚细节还有待进一步完善.
| [1] |
Mcknight DH, Chervany NL. What trust means in E-commerce customer relationships: An interdisciplinary conceptual typology. International Journal of Electronic Commerce, 2001, 6(2): 35-59. DOI:10.1080/10864415.2001.11044235 |
| [2] |
罗菁. 揭开职场上神秘“背调”的面纱. 劳动保障世界, 2019(34): 30. DOI:10.3969/j.issn.1007-7243.2019.34.018 |
| [3] |
田有亮, 骆琴. 基于改进Merkle-Tree认证方法的可验证多关键词搜索方案. 通信学报, 2020, 41(9): 118-129. |
| [4] |
Nakamoto S. Bitcoin: A peer-to-peer electronic cash system. http://www.bitcoin.org/bitcoin.pdf. (2009-01-03).
|
| [5] |
翟社平, 陈思吉, 汪一景. 基于区块链的数字版权存证系统模型研究. 计算机工程与应用, 2020, 56(19): 13-21. |
| [6] |
Mohamed K, Aziz A, Mohamed B, et al. Blockchain for tracking serial numbers in money exchanges. Intelligent Systems in Accounting, Finance and Management, 2019, 26(4): 193-201. DOI:10.1002/isaf.1462 |
| [7] |
Guo Y, Liang C. Blockchain application and outlook in the banking industry. Financial Innovation, 2016, 2(1): 24. DOI:10.1186/s40854-016-0034-9 |
| [8] |
Chen LX, Lee WK, Chang CC, et al. Blockchain based searchable encryption for electronic health record sharing. Future Generation Computer Systems, 2019, 95: 420-429. DOI:10.1016/j.future.2019.01.018 |
| [9] |
Song DX, Wagner D, Perrig A. Practical techniques for searches on encrypted data. Proceedings of 2000 IEEE Symposium on Security and Privacy. Berkeley: IEEE, 2000. 44–55.
|
| [10] |
Cao N, Wang C, Li M, et al. Privacy-preserving multi-keyword ranked search over encrypted cloud data. IEEE Transactions on Parallel and Distributed Systems, 2014, 25(1): 222-233. DOI:10.1109/TPDS.2013.45 |
| [11] |
Sun WH, Liu XF, Lou WJ, et al. Catch you if you lie to me: Efficient verifiable conjunctive keyword search over large dynamic encrypted cloud data. Proceedings of 2015 IEEE Conference on Computer Communications. Hong Kong: IEEE, 2015. 2110–2118.
|
| [12] |
Naveed M, Prabhakaran M, Gunter CA. Dynamic searchable encryption via blind storage. Proceedings of 2014 IEEE Symposium on Security and Privacy. Berkeley: IEEE, 2014. 639–654.
|
| [13] |
Hu SS, Cai CJ, Wang Q, et al. Searching an encrypted cloud meets blockchain: A decentralized, reliable and fair realization. IEEE Conference on Computer Communications (IEEE INFOCOM 2018). Honolulu: IEEE, 2018. 792–800.
|
| [14] |
Androulaki E, Barger A, Bortnikov V, et al. Hyperledger fabric: A distributed operating system for permissioned blockchains. Proceedings of the 13th EuroSys Conference. New York: ACM, 2018. 30.
|
| [15] |
Miau S, Yang JM. Bibliometrics-based evaluation of the Blockchain research trend: 2008 - March 2017. Technology Analysis & Strategic Management, 2018, 30(9): 1029-1045. |
| [16] |
张亮, 刘百祥, 张如意, 等. 区块链技术综述. 计算机工程, 2019, 45(5): 1-12. |
| [17] |
范吉立, 李晓华, 聂铁铮, 等. 区块链系统中智能合约技术综述. 计算机科学, 2019, 46(11): 1-10. DOI:10.11896/jsjkx.190300013 |
| [18] |
李经纬, 贾春福, 刘哲理, 等. 可搜索加密技术研究综述. 软件学报, 2015, 26(1): 109-128. DOI:10.13328/j.cnki.jos.004700 |
| [19] |
黄穗, 陈丽炜, 范冰冰. 基于CP-ABE和区块链的数据安全共享方法. 计算机系统应用, 2019, 28(11): 79-86. DOI:10.15888/j.cnki.csa.007144 |
| [20] |
Xhafa F, Wang JF, Chen XF, et al. An efficient PHR service system supporting fuzzy keyword search and fine-grained access control. Soft Computing, 2014, 18(9): 1795-1802. DOI:10.1007/s00500-013-1202-8 |
| [21] |
Liu ZL, Li T, Li P, et al. Verifiable searchable encryption with aggregate keys for data sharing system. Future Generation Computer Systems, 2018, 78: 778-788. DOI:10.1016/j.future.2017.02.024 |
| [22] |
Cash D, Jaeger J, Jarecki S, et al. Dynamic searchable encryption in very-large databases: Data structures and implementation. Proceedings of the Network and Distributed System Security Symposium. 2014. 23–26.
|
| [23] |
Rajkovic V. UCI machine learning repository. http://archive.ics.uci.edu/ml/datasets/Nursery. (1997-06-01).
|
 2021, Vol. 30
2021, Vol. 30


