随着信息技术的飞速发展以及互联网技术在生活中的普及, 传统媒体的内容形式逐渐向数字转变, 数字技术使得图像、音频、视频和文本等一些多媒体数据储存和传播变得非常的方便^[1], 版权侵犯、内容篡改等违法行为变得更加容易, 数字作品的版权、完整性和有效性得不到保障, 使得严重损害了作品所有者的利益, 因此解决版权保护和信息安全问题变得尤为重要^[2].

数字水印^{[3, 4]}是信息安全领域的研究热门问题, 可逆水印隐藏不仅能从载密图像中提取出秘密信息, 还能将载体图像无损还原. 现有的加密图像可逆水印隐藏方法分为以下几类: (1)加密前对图像不做处理, 通过修改加密后数据以嵌入水印信息^[5-8]; (2)加密后通过压缩密文数据腾出空间以嵌入水印信息^[9-11]; (3)加密前对载体图像先进行预处理, 预留出空间进行水印信息嵌入^[12-14]; (4)加密数据阶段使用公钥机制, 水印嵌入阶段利用加密技术的同态性^[15]. 除此之外, 在水印提取和图像恢复阶段, 根据水印提取和图像恢复是否可以独立操作, 算法分为可分离加密域可逆水印算法和不可分离加密域可逆水印算法, 其中不可分离的算法可以利用图像像素的平滑度来实现可逆性^[16], 但是这种方法的提取水印和恢复图像的质量与分块的大小有关; 可分离算法^[16-18]可以解决当嵌入率比较高时无法准确提出水印的问题. 文献[18]利用压缩技术保证了信息的完全提取, 同时还提高了嵌入率, 文献[17, 18]中的算法嵌入率和恢复图像质量都有了提高. 文献[19]提出将直方图平移随机化, 增强了算法的安全性, 并通过多层级嵌入增加嵌入容量. 文献[20]中的算法通过直方图平移的方法嵌入秘密信息, 具体方法是将图像进行分块, 然后将块内像素分组, 最后建立差值直方图. 文献[21]利用不同的加密方法对原始图像加密, 利用同态加法、差值扩展方法分别在高、低位平面嵌入水印信息.

文献[17]中提出的可分离加密域可逆数据隐藏算法将水印信息隐藏到高位上并且结合预测算法实现了可逆性, 由于水印信息嵌到高位导致直接解密图像质量不高, 针对这个问题, 本文在嵌入水印信息之前对图像进行标记, 通过图像标记将水印信息有选择的嵌在第7或8位, 在相邻像素相关性基础上通过一种自适应差值算法实现水印提取和图像恢复, 既能保证无失真地恢复图像又能提高解密的图像质量.

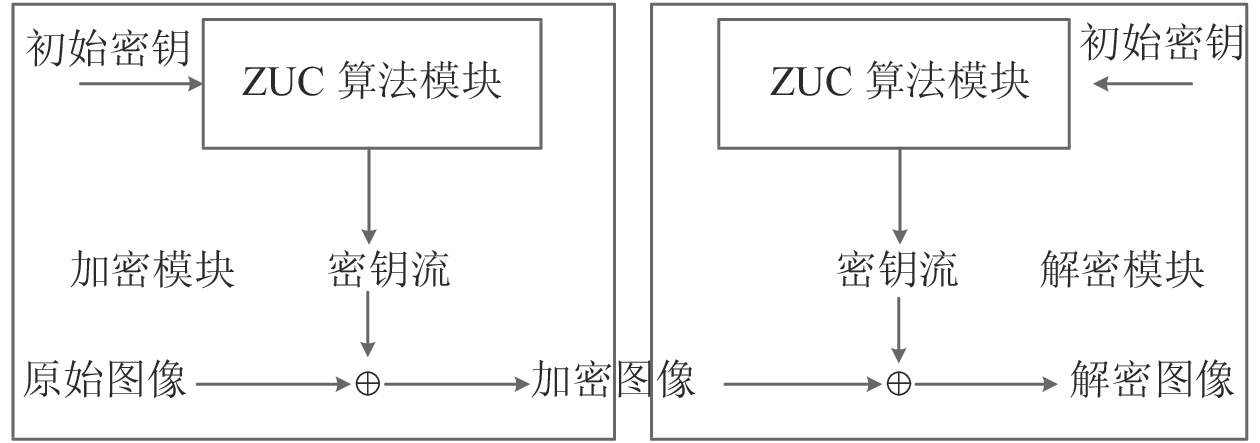
1 相关知识 1.1 祖冲之算法

祖冲之算法(ZUC)是一种流密码算法. 其加密过程为, 将ZUC算法产生的密钥和输入的明文按位进行异或运算; 解密过程为, 使用加密密钥和密文按位进行异或运算, 过程如图1所示.

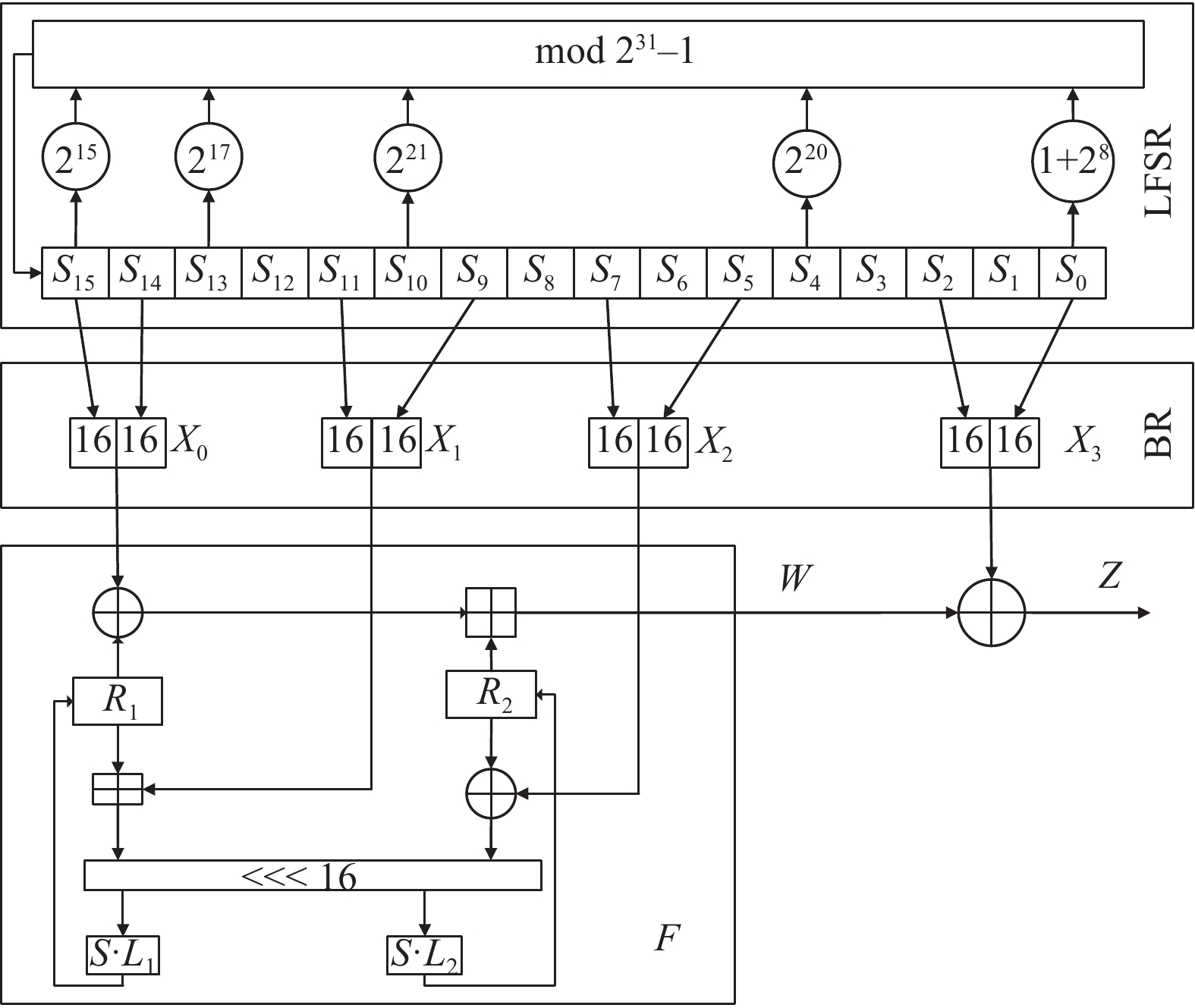
ZUC算法结构设计^[22]如图2所示, 分别包括LFSR线性反馈移位寄存器、BR比特重组以及非线性函数F. LSFR的每一个寄存器都是31 bit, BR实现LFSR数据单元到非线性函数F和密钥输出Z的数据转换.

1.2 加密域可逆水印技术

加密域可逆水印不仅加密域嵌入的水印信息可以完整提取, 而且水印经提取后原始载体也可以无损地恢复. 文献[16]利用自然图像的空间相关性实现了可逆性; 文献[17]提出的算法在恢复阶段使用图像预测的方法实现了算法的可逆性. 该技术一般用于多媒体作品的完整性认证, 广泛适用于一些保密强、安全密级高以及精度要求高的领域, 如医学领域、军事领域、电子发票、法律文书图片等.

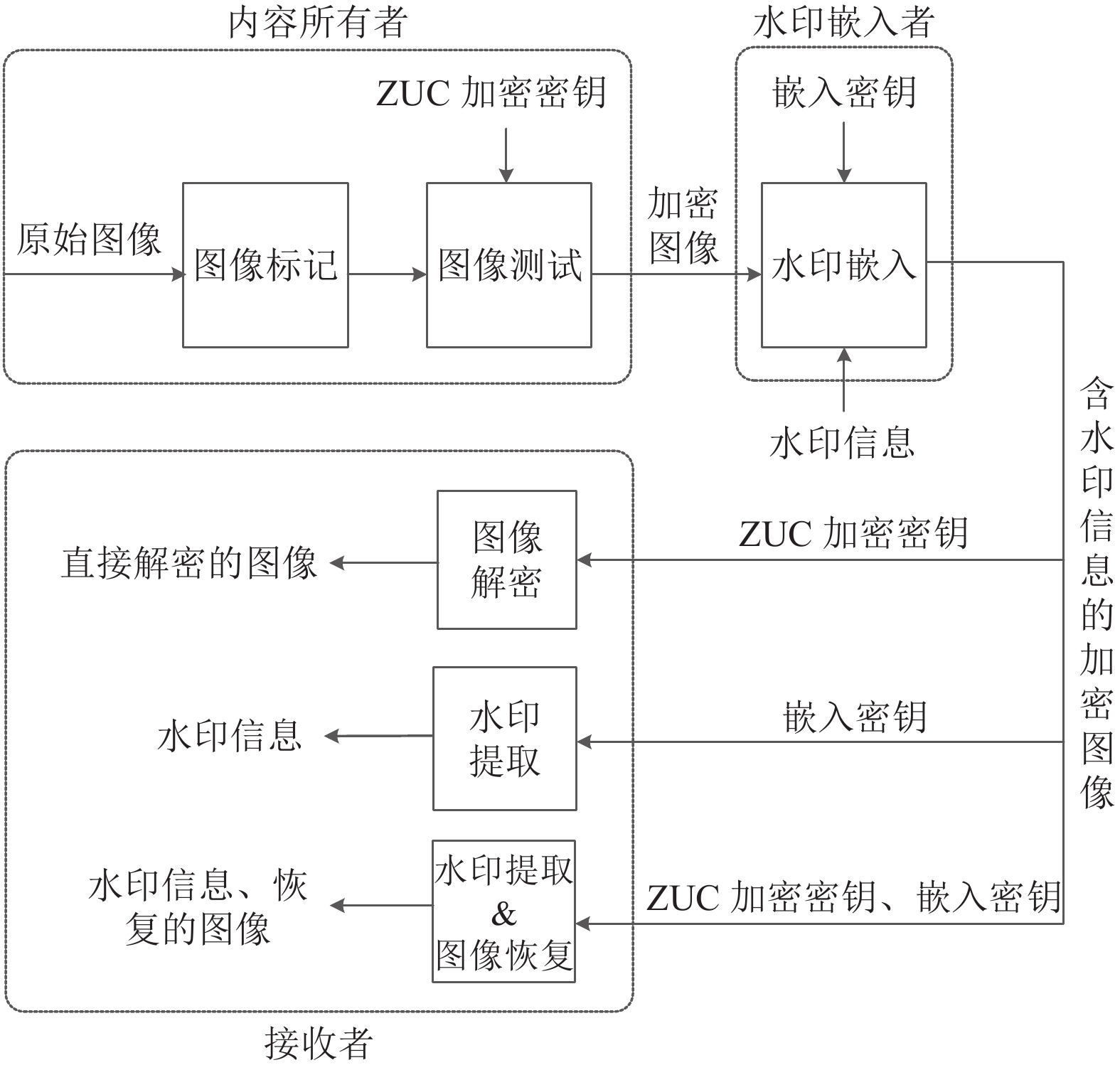
2 基于ZUC算法可分离加密图像可逆水印算法设计

算法流程图如图3所示. 首先内容所有者先对载体图像进行图像标记并生成位置图, 然后利用ZUC算法对原始载体图像加密得到加密图像, 其次水印嵌入者得到加密图像后根据位置图将水印信息嵌入到加密图像中, 得到含水印信息的加密图像. 最后, 接收者利用嵌入密钥提取出水印信息. 接收者使用加密密钥得到直接解密的图像. 接收者使用嵌入密钥和加密密钥进行出水印信息提取以及恢复原始图像.

2.1 图像标记

在嵌入水印信息之前对图像进行标记, 通过标记判断嵌入的位置, 能保证恢复图像和直接解密图像具有较高的质量. 图像标记示意图如图4 所示, 加密前的选中像素用 b(d)表示, 解密后含有水印信息的像素用D(d)表示, 其中d = 1, 2, …, L, L为水印信息的长度. 水印信息嵌入第7位且正确恢复b(d)有两种情况: 第一种情况是b(d)的第7位为0, 在恢复阶段, 将D(d)的第7位置1得到D₀(d), 置0得到 D₁(d). 这时D₁(d) 为该像素的真实值, 即D₁(d)=b(d). 因此, 在判决阶段使D_out(d)= D₁(d)就能正确恢复该像素. 由式(15)可知, 当预测值D_est(d)与 D₁(d) 更接近时才能使D_out(d) =D₁(d). 因为D₀(d) − D₁(d) = 2, 由此可以得出在第一种情况下满足条件D_est(d) < b(d) + 1, 可以正确恢复原始像素. 第二种情况是b(d)的第7位为1, 同理可得正确恢复的条件为D_est(d)≥b(d) −1.

内容所有者对每个像素测试并将测试结果标记在位置图上. 若该像素的第7位是0且满足D_est(d) < b(d)+1, 或第7位是1且满足D_est(d)≥b(d) −1, 则记为0; 否则记为1. 水印嵌入者在得到加密图像和位置图后使用嵌入密钥进行水印嵌入, 如果选中像素在位置图上的标记为0, 则水印信息嵌在第7位. 如果选中像素在位置图上的标记为1则嵌在第8位.

2.2 图像加密

首先内容所有者使用ZUC算法对图像进行加密. 对于一个大小为M×N的灰度图像, 灰度值I_i,j的取值范围为[0, 255], (i,j)表示像素的位置( $1 \le i \le M,1 \le j \le N$ ), I_i,j可表示为8位二进制 ${b_{i,j,1}},{b_{i,j,2}},\cdots,{b_{i,j,8}}$ 则:

$ {b_{i,j,k}} = \left\lfloor {\frac{{{I_{i,j,k}}}}{{{2^{k - 1}}}}} \right\rfloor \mod 2,\; k=1, 2,\cdots,8 $

(1)

其中, $\left\lfloor \cdot \right\rfloor $ 表示向下取整, 内容所有者利用ZUC算法产生密钥流 ${r_{i,j,k}}$ , 与图像像素各比特位 ${b_{i,j,k}}$ 进行异或运算.

$ {e_{i,j,k}} = {b_{i,j,k}} \oplus {r_{i,j,k}},\;k=1, 2,\cdots,8 $

(2)

所得到的 ${e_{i,j,k}}$ 即加密后的结果.

由式(3)得到加密图像:

$ {E_{i,j}} = \sum\limits_{k = 1}^8 {{e_{i,j,k}}} \times {2^{k - 1}}, \; k=1, 2,\cdots,8 $

(3)

2.3 水印信息嵌入

内容所有者将加密图像和位置图传送给水印嵌入者, 假设L为水印信息是长度S(1), S(2), …, S(L). 首先, 水印嵌入者将加密图像的像素分为用来存放嵌入信息和存放没有嵌入信息两个集合, 其中用来存放嵌入信息集合用Q_emb表示, 存放没有嵌入信息的集合用Q_ban表示. 在初始阶段令Q_emb初始值为空集, Q_ban初始值为加密图像的上下左右4个像素即Q_ban= $\left\{ (i,j)|i = 1 \vee \right. $ $ \left. j = 1 \vee i = M \vee j = N \right\}$ . 然后, 水印嵌入者使用嵌入密钥随机选取与水印信息长度相同的L个像素, 保证选取的像素不属于Q_ban, 将选取的像素放入用来存放嵌入信息集合Q_emb中, 并将该选中像素相邻的上下左右4个像素放入Q_ban中, 如图5所示, t₁, t₂, t₃, t₄表示4个相邻像素. 这样对于每个用来嵌入的像素, 与它相邻的4个像素均不能用来嵌入水印信息, 所以这4个像素的值在嵌入前后保持不变. 最后, 水印嵌入者结合位置图利用式(4)将选中像素B(d)的第T位数值b替换成秘密信息S(d), 从而完成水印的嵌入.

标记的位置图决定了水印嵌入的位置, 如果该像素在位置图上的标记为0, 说明水印嵌在第7位该像素可以完全恢复, 为了得到更高质量的直接解密的图像, 将水印信息嵌在第7位. 若该像素在位置图上的标记为1, 说明嵌在第8位该像素可以完全恢复, 为了得到更高质量的恢复载体图像, 将水印信息嵌在第8位.

$ b = \left\lfloor {\dfrac{{B(d)}}{{{2^{(8 - T)}}}}} \right\rfloor \boldsymbolod 2,\;d=1,2,\cdots,L $

(4)

$ B'(d) = B{\rm{(}}d) - b \times {2^{(8 - T)}} + S(d) \times {2^{(8 - T)}},\;d=1,2,\cdots,L $

(5)

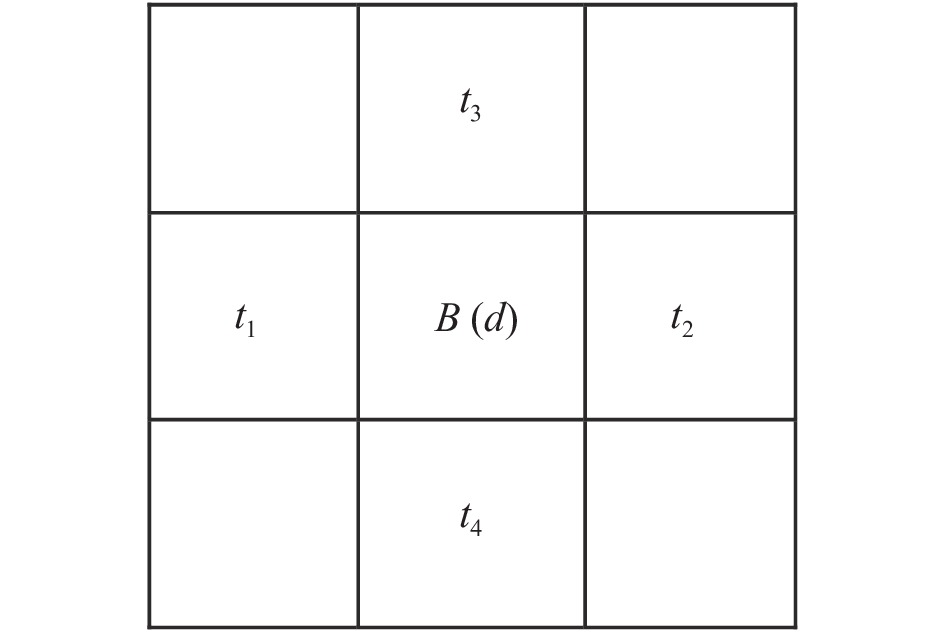
式中, b表示选中像素第T位的值, $B'(d)$ 是含有水印信息的加密像素.

2.4 水印信息提取及图像恢复

接收者利用加密密钥解密得到含水印信息的解密图像. 接收者利用ZUC算法产生密钥流r_i,j,k, 并与 ${e'_{i,j,k}}$ 逐位进行异或运算.

$ {b'_{i,j,k}} = {e'_{i,j,k}} \oplus {r_{i,j,k}},\; k=1,2,\cdots,8 $

(6)

所得到的 ${b'_{i,j,k}}$ 为直接解密的结果, ${e'_{i,j,k}}$ 为含有水印信息的加密数据.

接收者使用嵌入密钥提取水印信息, 首先根据嵌入密钥得到含有水印信息的L个像素 $B'(1),B'(2),\cdots,B'(L)$ ; 再根据式(7)和位置图提取出水印信息S(d), 式中T的值由该像素在位置图上的标记决定, 若标记为0, 则T=7; 若标记为1则T=8.

$ S(d) = \left\lfloor {\frac{{B'(d)}}{{{2^{(8 - T)}}}}} \right\rfloor \boldsymbolod 2,\;d=1,2,\cdots,L $

(7)

接收者同时使用加密密钥和嵌入密钥, 既可以提取水印, 也可以恢复原始载体图像. 首先, 利用加密密钥对图像进行解密得到直接解密图像, 然后根据嵌入密钥得到含有水印信息的解密像素 $D(1),D(2),\cdots,D(L)$ , 最后通过自适应差值算法得到嵌入像素的预测值. 取出每个含有水印信息的像素D(d)的4个相邻像素t₁, t₂, t₃, t₄, 将t₁, t₂, t₃, t₄代入式(8)计算出斜率g, 然后对照表1得到相应的类型t, 再对照表2得到对应的预测系数 ${\alpha _1},{\alpha _2},{\alpha _3},{\alpha _4}$ , 最后将预测系数代入式(9)计算出预测值D_est(d).

$g = \left| {{t_1} - {t_2}} \right| - \left| {{t_3} - {t_4}} \right|$

(8)

${D_{\rm est}} = {\alpha _1}{t_1} + {\alpha _2}{t_3} + {\alpha _3}{t_2} + {\alpha _4}{t_4}$

(9)

计算出预测误差后利用式(10)–式(12)将该像素的第T位置1得到D₀(d), 置0得到D₁(d), 如果该像素在位置图标记为0, 则T=7; 如果该像素在位置图标记为1, 则T=8.

$ b' = \left\lfloor {\frac{{D(d)}}{{{2^{(8 - T)}}}}} \right\rfloor \boldsymbolod 2,\; d=1,2,\cdots,L $

(10)

$ {D_0}(d) = D{\rm{(}}d) - b' \times {2^{(8 - T)}} + 1 \times {2^{(8 - T)}},\;d=1,2,\cdots,L $

(11)

$ {D_1}(d) = D{\rm{(}}d) - b' \times {2^{(8 - T)}}, \;d=1,2,\cdots,L $

(12)

其中, b′为D(d)第T位的值.

然后由式(13), 式(14)计算出预测误差R₀(d), R₁(d).

$ {R_0}(d) = \left| {{D_0}(d) - {D_{\rm est}}(d)} \right| $

(13)

$ {R_1}(d) = \left| {{D_1}(d) - {D_{\rm est}}(d)} \right| $

(14)

最后比较预测误差R₀(d), R₁(d)的大小, 误差较小的像素值作为恢复的像素值.

${D_{{\mathop{\rm out}\nolimits} }}(d) = \left\{ \begin{array}{l} {D_0}(d),\;{R_0}(d) \le {R_1}(d)\\ {D_1}(d),\;{R_0}(d) > {R_1}(d) \end{array} \right.$

(15)

式中, D_out(d)即为恢复的像素值.

3 实验结果分析

实验选取载体图像为6个大小为512×512像素的灰度图像, 以大小为64×64像素的图像作为水印图像进行实验. 如图6所示, 它们包括Lena, Peppers, Baboon, Boat, Lake, Plane以及水印图像“BIGC”.

3.1 算法完整性测试

以图6(a)作为原始载体图像, 图6(g)作为待嵌入的大小为64×64像素的水印为例, 共嵌入4096位水印信息, 嵌入率为0.15625; 图7(b)为使用ZUC算法加密后得到的加密图像; 包含水印信息的加密图如图7(c)所示. 接收者接收到含有水印信息的加密图后先利用加密密钥解密图像得到含有水印信息的解密图如图7(d)所示; 再利用嵌入密钥从解密后的图像中成功地提取出嵌入的水印, 完整地恢复出原始图像. 提取水印和恢复图像如图7(e), 图7(f)所示.

3.2 算法安全性分析

通过计算图像熵来分析加密图像安全性. 图像中平均信息量用信息熵表示. 信息熵计算如下:

$H(X) = - \sum\limits_{i = 0}^{255} {p({X_i})} {\log _2}p({X_i})$

(16)

其中, p(X_i)°表示图像中灰度值为X_i的像素所占的比例, H(X) 的最大理论值为8, 通常, 熵越高, 图像越安全. 图8为6个测试图像的加密图, 表3显示了原始图像和加密图像的熵值; 由表3可知, 加密图像的所有熵值都非常接近最大理论值8, 而原始图像的熵值却远离最大理论值, 这说明使用ZUC加密可以保证算法的安全性.

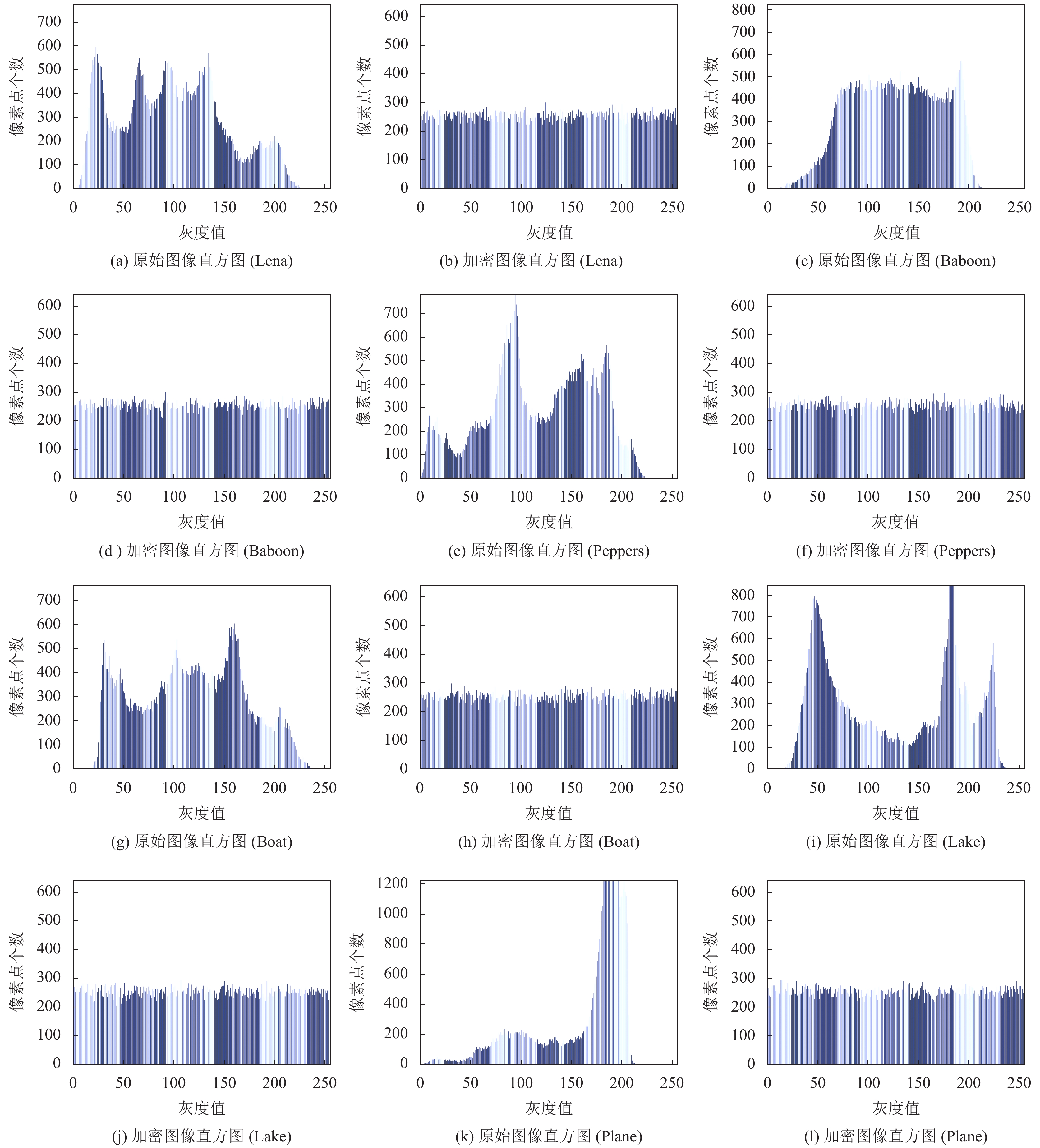
通过实验得到6组图像的原始图像和加密图像的直方图如图9所示. 图9(a)、图9(c)、图9(e)、图9(g)、图9(i)、图9(k)为原始图像的直方图. 图9(b)、图9(d)、图9(f)、图9(h)、图9(j)、图9(l)是加密后的直方图, 通过对比可以明显看出较为平滑, 像素的比例较为均匀, 说明加密后的图像安全性更高.

3.3 算法嵌入能力测试

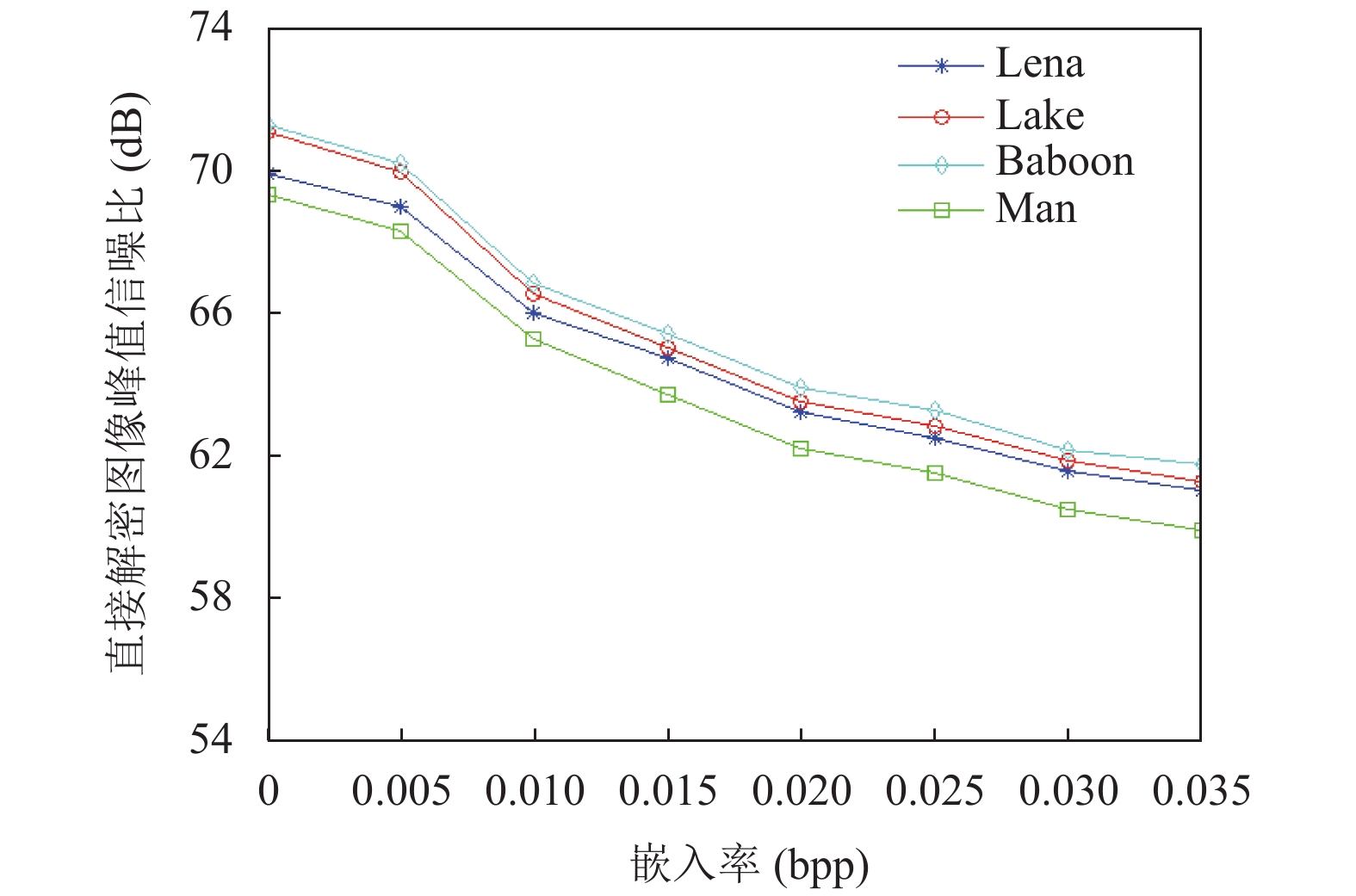
图10展示了对于图像 Lena, Lake, Baboon, Man嵌入量与解密图像峰值信噪比的关系. 可以看出随着嵌入率的增加, 含水印的解密图像仍拥有较高的PSNR值.

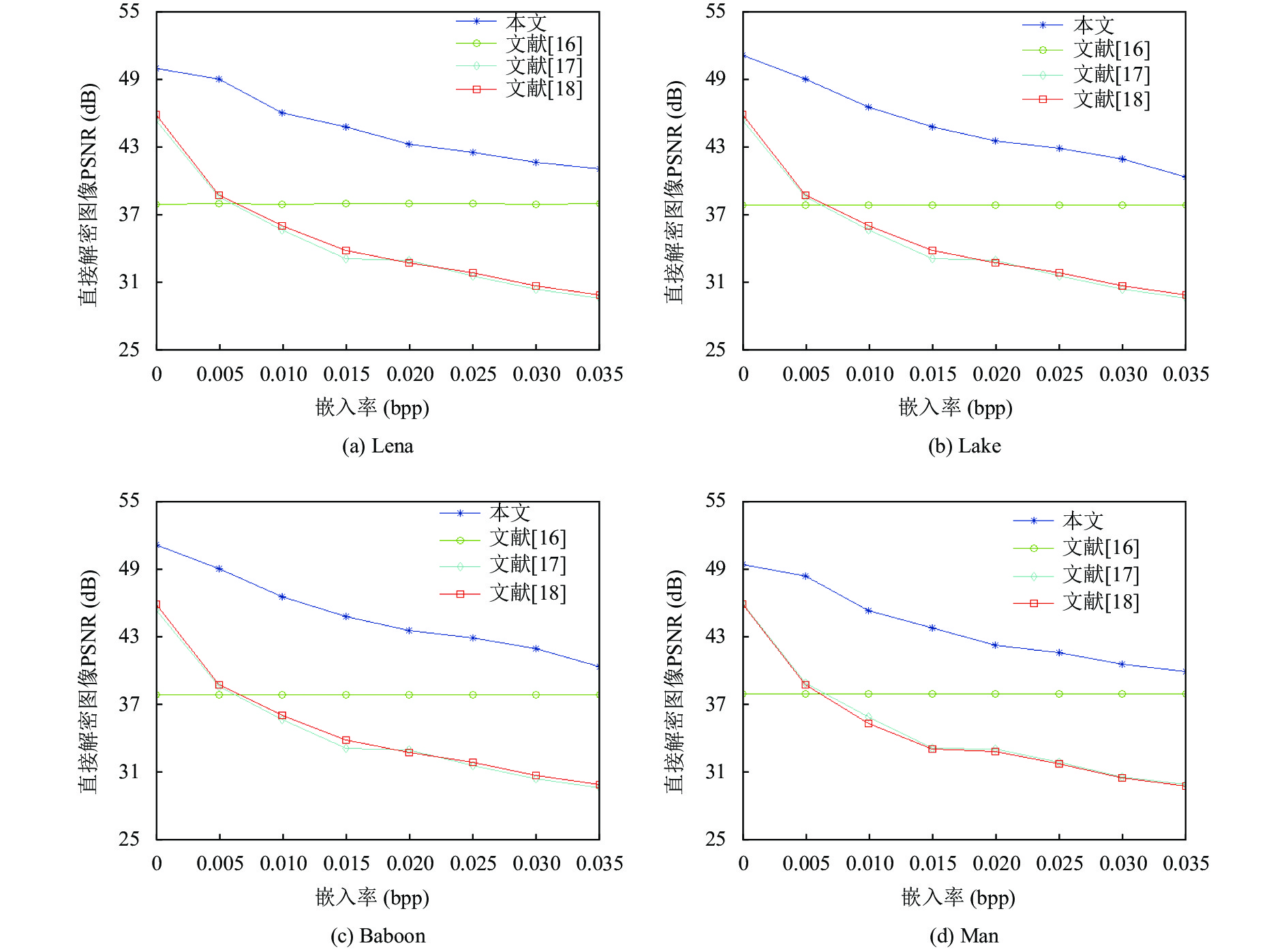
本文算法与文献[16–18]的算法嵌入量与PSNR对比情况如图11所示.

从图11可以看出, 本文算法直接解密图像的PSNR大于文献[17, 18], 因此本文提出的方案具有更好的整体性能.

表4–表7列出了不同嵌入率本文算法与文献[17,18]算法PSNR值的对比. 通过表格对比可以看出本文算法的直接解密和恢复图像的PSNR值最高, 说明该算法优于文献[17,18].

4 结论

本文提出了一种可分离加密图像可逆水印算法, 与其他算法不同的是该算法在用ZUC算法加解密图像, 具有较高的安全性; 算法在嵌入水印信息前进行图像测试并标记, 保证了嵌入水印信息的像素在接收方能够完全恢复, 同时提高了恢复图像和直接解密图像的质量; 水印嵌入者用水印信息替换选中像素的第T(T=7或8)位完成水印信息的嵌入; 接收者根据嵌入密钥和加密密钥可以提取水印和恢复出原始载体图像. 通过实验对比分析了原始图像和加密图像的熵以及原始图像和加密图像的直方图, 证明了使用ZUC算法加密图像具有较高的安全性. 通过实验计算直接解密图像和恢复图像的PSNR值和NC值, 证明了本文算法的性能优于文献[18]的算法.

本文算法具有较高的安全性和性能, 但是由于嵌入水印时将图像分成了嵌入水印集合和非嵌入水印集合, 这使得水印的嵌入量有了一定的影响, 接下来的研究工作将从如何提高算法的嵌入量入手.