2. 深圳市网联安瑞网络科技有限公司, 深圳 518038;
3. 中电科新型智慧城市研究院有限公司, 深圳 518026
2. Shenzhen CyberArey Network Technology Co. Ltd., Shenzhen 518038, China;
3. CETC New Smart City Research Institute Co. Ltd., Shenzhen 518026, China
大数据[1]的发展, 带动了各种分布式计算、存储框架的发展. 其中Spark、Flink等作为开源主流的分布式计算框架, HBase、MemSQL、Elasticsearch等作为开源主流的分布式存储框架. 但是计算存储框架都存在分区不合理引发数据倾斜[2, 3]而导致的集群负载不均衡现象, 大大降低了应用的分析性能. 因此, 为了提高集群数据分析性能, 有必要对数据分区策略进行研究, 最终提高数据分析的响应速度, 快速为企业提供决策, 增加效益.
分布式存储框架Elasticsearch[4]采用主从结构, 使用路由 Hash[5]作为存储方式, 以数据分区Shards作为物理分区, 底层依托Lucene倒排索引结构, 并且支持文本分词, 非常适合关键词搜索分析. Spark 同样采用主从结构, Master 节点(主节点)管理整个集群的资源, Worker 节点(从节点)管理各计算节点的资源, 定期向 Master 节点汇报节点资源情况, 并启动 Executor 进行计算.
Spark-Elasticsearch[6]集成的应用场景, 采用local方式读取数据分析的方式, 通过Elasticsearch Spark Connect组件将二者集成, Spark中Master与Elasticsearch中主节点连接起来, 然后Spark的Worker节点可以通过Master节点获取到Elasticsearch中主节点的元数据信息, 其元数据信息包括数据有哪些分区及各分区存储在哪些节点上, 从而实现程序进行数据分析过程中, Spark的Worker节点利用esRDD接口本地化并行地从Elasticsearch存储节点进行数据读写、计算分析, 如图1所示. Elasticsearch中最小物理分区是Shard, 目前每个节点默认分配相同的Shard数, 这会因为集群节点资源的异构性[7]导致节点处理能力的不同而引发节点之间数据倾斜问题. 由于此框架中Spark采用local分析数据的方式, 即数据在哪个节点上面, 就在相应节点上进行分析处理, Elasticsearch中的Shard数目直接反映 Spark 中的 RDD task 数目, 即任务量与分区数呈正相关关系, 如果采用默认分区方式会导致严重负载不均衡现象, 如很多分区块分布在负载高的数据节点上进行处理分析, 那么会拖慢整个作业完成效率, 因为 Spark 任务调度结束是所有task都完成的时刻. 现实应用中, 数据倾斜问题普遍存在, 由其引起的处理节点负载不均衡是 Spark-Elasticsearch集成框架应用不可避免的问题.

|
图 1 Spark读Elasticsearch中数据机制图 |
有关动态分区解决负载均衡性的相关研究中, 李想等人[8]提出一种改进的遗传算法的数据分配策略, 采用自适应交叉和变异算子策略. 王晓燕等人[9]采用Nash-Pareto优化均衡策略协同自动数据分布. 王新友等人[7]设计一种基于时间序列模型二次指数平滑法对引航事故进行预测, 减少引航事故的发生. 杨华芬[10]提出一种基于优化FA模型的动态迁移算法, 首先构建动态迁移框架, 确定数据中心和网络节点的拓扑结构, 然后利用FA仿生群智能算法在数据中心区域范围内更新个体的位置并寻找最优解, 最后引入适应度函数和自适应惯性权重优化算法并扩大寻优范围, 实现大数据迁移成本最小化. 刘琨[11]采用一次平滑预测算法+客观熵值法权重模型, 通过确定节点负载情况来进行虚拟机资源迁移达到负载均衡效果. 陈涛等人[12]提出一种数据分布算法CCHDP, 将聚类算法和一致性Hash方法结合, 根据设备可用资源权重自适应调节分配数据. 宋怀明等人[13]设计了自适应散列和直方图相结合的数据分布策略, 动态调整节点负载均衡性. 王晶等人[14]设计了一种基于动态阈值的迁移时机判决算法与基于负载类型感知的选择算法相结合的虚拟机动态迁移策略, 最终根据虚拟机与目的节点的资源匹配度与迁移代价选择目的节点, 对高负载与低负载节点的虚拟机动态调整, 从而优化节点资源配置问题.
针对Spark-Elasticsearch集成框架进行数据分析的应用场景, 需要提出Elasticsearch分区策略来改善负载均衡性, 提高应用的响应速度. 因此本文提出一种基于节点负载的数据动态分区机制和策略. 基于节点负载的数据动态分区机制包括负载监测采集、预测、数据预分区、数据迁移等模块; 基于节点负载的数据分区策略采用二次平滑法预测节点负载, 结合了 AHP 和熵值指标权重法, 能够根据不同的数据分析应用得到相应的分区策略, 动态地调整系统的负载均衡性, 提高应用的响应速度.
2 基于节点负载的数据动态分区机制和策略针对Spark-Elasticsearch集成框架的应用场景, 即采用local方式读取数据分析的方式, 需要有效地将数据进行分布来提高系统的负载均衡性, 通过提高并行度来降低应用的响应时间. Spark的Worker节点local方式并行地从Elasticsearch存储节点进行数据读写、计算分析, 如图2所示. Elasticsearch中最小的物理单元是Shard, 而Elasticsearch中的Shards数目直接反映Spark中的RDD task数目.

|
图 2 Spark-Elasticsearch集成框架图 |
因为Spark并行访问Elasticsearch中的每个分区中的数据, 并将每个分区中的数据转化成自身的一个RDD分区, 由于Spark中的一个RDD分区对应一个task, 而task需要CPU来处理, 为了减少CPU资源的上下文切换, 充分利用CPU资源, 则Elasticsearch中的Shards数目的设置要适中, 不能过小或过大, 经相关技术人员进行长时间的研究测试, 一般选择可用CPU核数的2–3倍; 同时每个Shards中的数据需近似相等, 来提高task的并行度.
在数据预分区阶段, Elasticsearch的数据分布默认是每个节点的分区数目相同, 而这样会因为集群中每个节点资源的异构性导致节点处理能力的不同而引起节点之间的数据倾斜现象, 引发集群负载不均衡的问题. 集群节点偶然会出现负载瞬时高低峰值的情况而影响数据分区决策的拟定; 同时由于任务类型的不同, 如计算型、内存性、网络传输等任务类型会导致每种指标的权重不同, 需要确定每种指标权重来拟定数据分区策略; 如果数据已经分配完, 但集群在应用过程中可能会因为负载不均衡问题导致任务执行阻塞, 也可能因为节点的增删操作引发负载不均衡等问题, 在现实应用中都可能遇到.
因此, 为了解决上述问题, 需要设计相应的数据动态分区机制和策略来改善系统的负载均衡性来提高应用的响应速度.
2.1 数据动态分区机制为了动态调整集群负载均衡性来提高应用的响应速度, 提出了基于节点负载的数据动态分区机制, 如图3所示, 该机制包括集群节点资源的监测、采集, 数据的预分区、迁移等模块. 整个Spark-Elasticsearch集成集群一直处于应用使用中, 监测模块定时读取从节点中各个指标的负载信息, 动态地显示CPU、内存和带宽的利用率等信息; 然后通过资源采集模块将负载信息缓存起来, 并定期持久化到MySQL中, 为负载预测提供指标实时负载信息; 接着如果有大量数据进行导入时, 需要对每个节点的每种指标进行预测, 再通过指标权重判定方法获得每种指标的权重, 接着再依据负载预测后的指标信息与每种指标的权重值来获得每个节点的处理能力, 最后根据每个节点的处理能力进行数据分布, 完成数据的预分区; 如果集群在实际应用中出现严重的负载不均衡问题, 如达到了设定负载阈值, 则将高低负载节点加入到源、目标机队列中, 并结合迁移策略进行分区块的迁移.
2.2 数据动态分区策略本文基于节点负载来进行数据有效地分布, 要解决如下问题:
(1)初始情况下, 面对大量数据的导入, 数据预分区根据什么原则进行数据分布.
(2)可能因为某些应用执行完或者预分区不合理情况导致集群负载不均衡现象, 通过数据迁移调整负载.
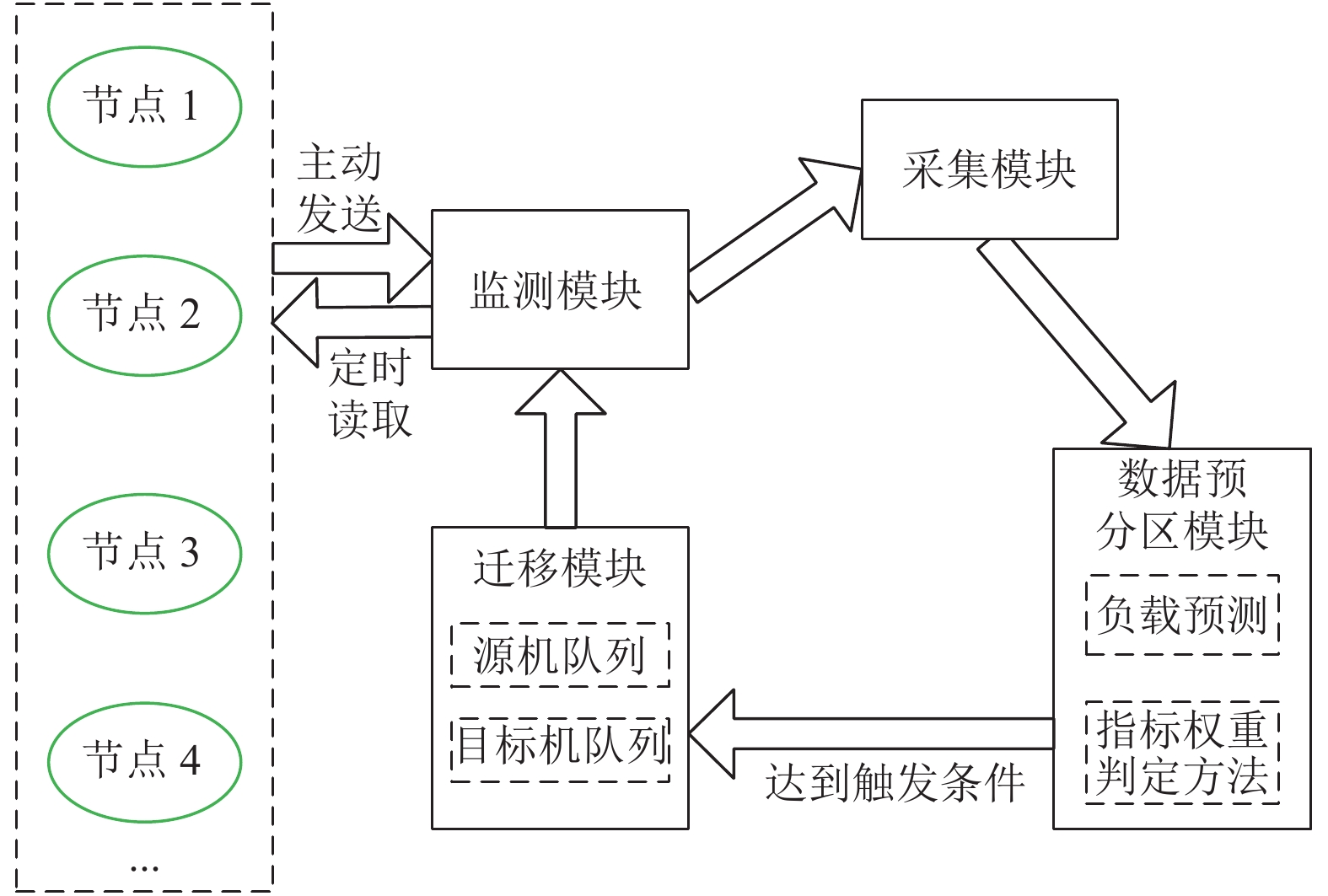
|
图 3 基于节点负载的数据动态分区机制流程图 |
本节通过动态分区策略来改善系统负载均衡性, 提高应用的响应速度. 采用二次平滑法预测节点负载, 结合了 AHP 和熵值指标权重法, 能够根据不同的数据分析应用得到相应的分区策略, 动态地调整系统的负载均衡性, 提高应用的响应速度.
2.2.1 数据预分区策略(1)负载预测
因数据预分区不合理、节点的宕机删除节点、增加节点进行水平扩展及出现负载极其不均衡问题等, 都需要进行分区块的迁移来平衡负载量, 采用二次指数平滑法负载预测模块来决定迁移量.
其中, n代表取的周期数, j代表第j个周期. 预测机制的流程如图4所示, 通过调整平滑系数α值来计算偏方差S, 取S最小时对应的平滑系数α值. n、d的值由用户设定.

|
图 4 预测机制流程图 |
(2)指标权重判定方法
因为Spark-Elasticsearch集成框架环境下的应用场景, 内存变化波动较小, 带宽和CPU变化波动较大, 如果只考虑客观熵值法则会影响内存的权重判定, 如果只考虑主观AHP权重法会忽略某些指标的重要性. 因此, 本文通过基于二次平滑负载预测法+主客观AHP与熵值指标权重集成法结合的指标权重判定方法算出每个节点的整体负载值, 最终再根据整体负载值来分配相应的数据分区数.
1) AHP
AHP由决策者对所有评价指标进行两两比较, 得到判断矩阵U=(Aij)n×n. 本论文取CPU利用率、内存利用率和带宽利用率作为负载的评价指标, 判断矩阵如下:
| $M = \left[ {\begin{array}{*{20}{c}} {CUR_1}&{MUR_1}&{BUR_1} \\ {CUR_2}&{MUR_2}&{BUR_2} \\ {\cdots}&{\cdots}&{\cdots} \\ {CUR_n}&{MUR_n}&{BUR_n} \end{array}} \right]$ |
其中, A1, A2, A3分别代表CPU利用率、内存利用率和带宽利用率对节点整体负载影响的权重值. 对每列进行归一化求取特征向量, 再对每行进行归一操作求取特征向量, 最后得到各指标的权重配比, 同时对判断矩阵A进行一致性检验, 证明判断矩阵的合理性, 最终可得到CPU、内存和带宽的主观权重分别为WS1, WS2, WS3, 并且WS1+WS2+WS3=1.
2) 熵值法
熵值法通过判断指标变化的离散度来反映该指标影响程度, 能够通过指标变异度客观地确定指标权重. 具体步骤如下:
① 通过测试过程得到各指标负载来构建负载信息决策矩阵M
| $M = \left[ {\begin{array}{*{20}{c}} {CUR_{1}}&{MUR_1}&{BUR_1} \\ {CUR_2}&{MUR_2}&{BUR_2} \\ {\cdots}&{\cdots}&{\cdots} \\ {CUR_n}&{MUR_n}&{BUR_n} \end{array}} \right]$ |
其中, n代表周期数, CUR、MUR和BUR分别代表CPU、内存和带宽的利用率.
② 对决策矩阵M每列做归一化处理得到矩阵R
| $R = \left[ {\begin{array}{*{20}{c}} {R_{11}}&{R_{12}}&{R_{13}} \\ {R_{21}}&{R_{22}}&{R_{23}} \\ {\cdots}&{\cdots}&{\cdots} \\ {R_{n1}}&{R_{n2}}&{R_{n3}} \end{array}} \right]$ |
其中,
③ 利用熵公式计算指标不确定度
用E表示某种指标的熵, 公式如下:
| $E_{j} = - K\sum\limits_{j = 1}^n R_{ij}\ln (R_{ij})$ |
其中, Ej代表指标的熵值, 常数K=1/ln(n), 这样能保证0≤E≤1, 即E最大为1. 当某个属性下各值的贡献度趋于一致时, E趋于1, 可看出属性列值差异性大小可影响权系数大小, 因此可定义Dj为某个指标的贡献度, Dj = 1−Ej.
④ 计算每种指标的客观权重值, 公式如下:
| $A = \left[ {\begin{array}{*{20}{c}} A&{A_{1}}&{A_{2}}&{A_{3}} \\ {A_{1}}&{A_{1}/A_{1}}&{A_{1}/A_{2}}&{A_{1}/A_{3}} \\ {A_{2}}&{A_{2}/A_{1}}&{A_{2}/A_{2}}&{A_{2}/A_{3}} \\ {A_{3}}&{A_{3}/A_{1}}&{A_{3}/A_{2}}&{A_{3}/A_{3}} \end{array}} \right]$ |
WO1, WO2, WO3代表内存、CPU和带宽对于节点负载影响的客观权重值, 并且WO1+WO2+WO3=1. 先通过输入每种指标不同周期负载值矩阵, 再计算每种指标客观权重值, 最后通过熵值法计算得到每种指标的客观权重值.
3) 主客观AHP和熵值法权重集成法
真实情况可能出现主、客观指标权重设计的弊端问题, 为了减少弊端影响性. 因此本发明设计主客观集成的方法来解决此类问题, 平衡两者的权重偏差. 集成权重公式如下:
| $w_{i} = \beta \times WS_{i} + (1 - \beta ) \times WO_{i}$ |
其中, β为主客观权重调整系数, wi为最终节点负载的权重, 其中i=1,2,3, 并且w1+w2+w3=1. 输入每种指标的主客观权重值, 再通过主客观权重集成法得到每种指标的集成权重值.
4) 节点的数据分布
首先, 由前面模块得到了内存、CPU、带宽3种指标在负载中所占的主客观集成权重大小后, 分别为w1, w2, w3.
然后, 通过每种指标权重计算得到每个节点的处理能力, 公式如下:
| $ CA_{i} = w_1 \times (1 - CAU_i) + w_2 \times (1 - MAU_i) + w_3 \times (1 - BAU_i) $ |
其中, CAUi, MAUi, BAUi分别代表指标预测后的CPU、内存、带宽利用率, i代表第i节点.
最后, 得出每个节点要分配的数据量的占比, 公式如下:
| ${{DP_i = }}\frac{{{{CA_i}}}}{{\displaystyle\sum\limits_{{{i}} = {{1}}}^{{m}} {{{CA_i}}} }}$ |
其中, DPi代表第i节点应分配的数据量占比, 有m个节点.
通过以上步骤后可知给集群中每个节点分配的数据量, 即相应的分区数.
2.2.2 数据迁移策略通过设置高低负载阈值来作为触发数据迁移的条件, 构造出源机和目标机的选择队列. 在数据预分区之后出现负载不均衡问题或者增删节点的情况, 需要选择源机和目标机来进行数据迁移, 源机作为待迁移数据的节点, 目标机作为接受迁移数据的节点, 并获得应迁移的分区数.
(1)源机选择
首先, 从负载缓存数组中读取内存利用率、CPU利用率和带宽利用率负载信息采用二次平滑法进行预测, 预测T个周期后的每种指标平均负载值.
然后, 将每种指标的负载利用率预测值与主客观权重集成方法得到每种指标权重值相结合, 进而得到每个节点的整体负载值Loadi. 负载值公式如下:
| $ Load_i = w_1 \times CUR_i + w_2 \times MUR_i + w_3 \times BUR_i $ |
其中, CURi, MURi, BURi和w1, w2, w3分别为预测后的CPU利用率、内存利用率、带宽的利用率和权重值.
接着, 比较每个节点的负载值Loadi和设置的阈值Hth, 如果某个节点的负载值超过阈值Hth, 则将该节点加入到高负载节点队列中.
然后, 按照Loadi值由大到小构成源机选择队列 S源={s1, s2, …, sm}.
最后, 从S源队列中选取源机. 对S源队列中的Load值按降序排列, 按Loadi值从大到小的顺序进行源机的选择.
(2)目标机选择
首先, 从负载缓存数组中读取内存利用率、CPU利用率和带宽利用率负载信息进行预测, 分别预测每种指标T个周期后的平均负载值.
然后, 将每种指标的负载利用率预测值与主客观权重集成方法得到每种指标的负载权重值结合, 代入主客观集成法计算, 进而得到每个节点的整体负载值Loadi.
接着, 将每个节点的负载值Loadi与设置的阈值Lth进行比较, 如果某个节点的负载值低于阈值Lth, 则将该节点加入到低负载节点队列中.
然后, 按照Loadi值构建由小到大目标机选择队列D目={d1, d2, …, dm}.
最后, 从D目队列中选取目标机. 对D目队列中的Load值按升序进行排列, 按Loadi从小到大的顺序进行目标机的选择.
(3)迁移的分区数
1)如果高低负载队列节点数相同, 即S源=D目. 则分别将高低负载节点队列的数据按照顺序进行匹配并行迁移, 迁移的分区数公式如下:
| $N_{\text{迁}} = \left| {\frac{{N_{\text{源}}{\rm{ - }}N_{\text{目}}}}{2}} \right|$ |
其中, N迁, N源, N目分别代表迁移的分区数, 源机中的分区数, 目标机中的分区数.
2)如果高负载队列节点数大于低负载节点数目, 即S源>D目. 则适当调整低负载阈值, 使低负载节点队列节点数目等于或近大于高负载节点队列节点数目, 接着按照上述迁移公式设定迁移的分区数.
3)如果高负载队列节点数目远小于低负载节点数目, 即S源<D目. 则适当调整高负载阈值, 使高负载节点队列节点数目等于或近小于低负载节点队列节点数目, 接着按照上述迁移公式设定迁移的分区数.
4)得到匹配的源机和目标机队列, 并知道了每组中源机应迁移的分区数, 采用并行进行迁移, 减少迁移开销.
通过以上步骤, 系统可实现负载均衡. 对于增删节点的突发情况, 同样可以采用此种迁移策略.
3 实验与分析本文针对Spark-Elasticsearch集成框架的应用场景, 在局域网下部署Spark-Elasticsearch集成集群环境, 集群中每个节点都是虚拟机, 本部分实验4个节点, 相关配置参数如表1所示, 设定的总分区数为32个分区, 利用某制造企业中的数据集, 验证基于负载预测和AHP、熵值集成权重法结合的数据动态分区策略的有效性.
| 表 1 Spark-MemSql集成框架机器参数 |
3.1 实验环境 3.2 实验数据
实验采用某制造业表product作为测试数据集, 如图5所示, 大约有5000万行数据. 每条数据主要包括产品长度、产品拉伸长度、产品重量等. 其中weight和length两列作为关联分析应用测试集, weight、drawlength、length三列可作为K-means应用测试集, 不同的应用利用不同的数据集做测试.
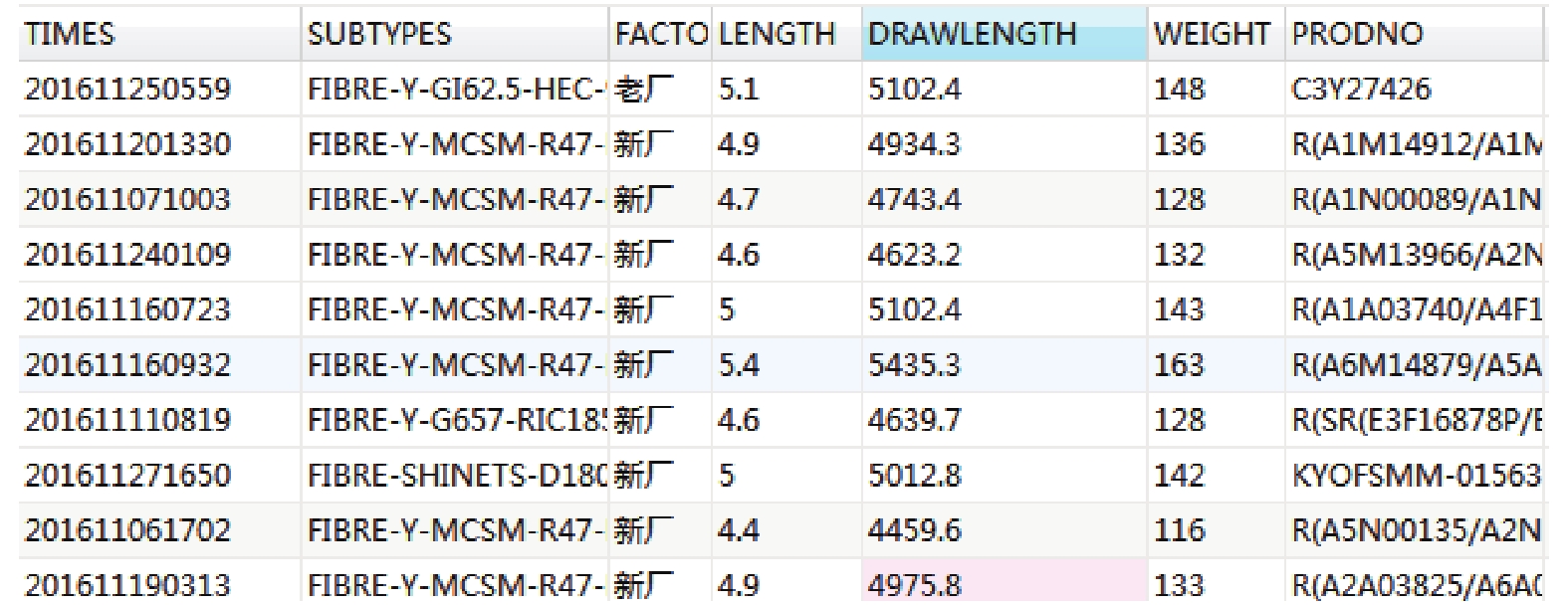
|
图 5 分区策略性能对比测试数据集 |
3.3 基于节点负载的动态分区策略实验分析
(1)对不同预分区策略进行性能对比测试. 本实验对weight和length两列做关联分析, 分析产品长度和重量之间的关联性; 对weight、drawlength、length三列做K-means聚类分析, 通过聚类分析分类. 通过比较默认预分区策略、负载预测+AHP权重法、负载预测+AHP与熵值集成权重法的3种不同预分区策略, 然后分别统计执行相同应用的时间, 验证方案的有效性.
(2)在Spark-Elasticsearch框架中如果出现集群负载不均衡现象, 结合迁移策略对源机和目标机的数据分区块进行迁移, 重复运行应用程序, 对迁移前后做性能对比, 验证方案的有效性.
3.3.1 预分区策略对比测试通过不同的预分区策略进行分区, 实验重复运行应用程序, 第1组实验进行关联分析的应用; 第2组实验进行K-means聚类分析的应用. 对执行时间进行对比, 验证不同分区方案的有效性.
(1)不同应用中不同指标平滑系数α
采用二次平滑预测算法最终获得不同应用场景下的不同指标的平滑系数α, 如表2和表3所示.
| 表 2 关联分析应用中不同指标的平滑系数α |
| 表 3 K-means聚类分析应用中不同指标的平滑系数α |
(2)利用AHP得出每种指标的权重
首先, 输入指标决策矩阵A:
| $A = \left[ {\begin{array}{*{20}{c}} A&{A_1}&{A_2}&{A_3} \\ {A_1}&1&2&9 \\ {A_2}&{\dfrac{1}{2}}&1&5 \\ {A_3}&{\dfrac{1}{9}}&{\dfrac{1}{5}}&1 \end{array}} \right]$ |
评判采用列与行进行两两比较, 其中A1, A2, A3分别代表CPU、内存、带宽; 然后, 计算随机一致性比率C.R.=C.I./R.I.=0.001<0.1, 说明决策矩阵设计合理; 接着, 利用AHP获得每种指标的权重值; 最后通过多次实验调整设置权重系数β为0.7, 得到集成权重值, 不同的应用场景结果分别如表4和表5所示.
| 表 4 关联分析应用中不同负载指标权重值对应表(%) |
| 表 5 K-means聚类分析应用中不同负载指标权重值对应表(%) |
(3)根据应用中预测的每种指标负载值和不同权重方法, 获得不同分区策略下每个节点的处理能力, 得出每个节点分区数的分区数, 如表6所示.
通过图6、图7所示, 分别执行关联分析和K-means聚类应用. 从整体上看默认分区策略效果最差, 本文设计的预测+AHP与熵值权重集成法分区策略最好, 并且随着数据量的增加, 效果越显著. AHP权重法是主观权重法, 没有根据实际应用场景进行权重配比, 有失客观性; Spark-Elasticsearch框架的数据计算是在内存中进行的, 因此内存使用较稳定, 而带宽使用变化程度较大, 但利用率很低, 如果只采用客观法会导致内存权重小、带宽权重较大的错误结果. 因此集成主客观权重会带来更好的结果. 执行不同的应用取得了同样的效果, 说明本文研究的预分区策略在处理相对独立任务的应用上具有推广性.
| 表 6 不同分区策略推荐的每个节点的分区数 |
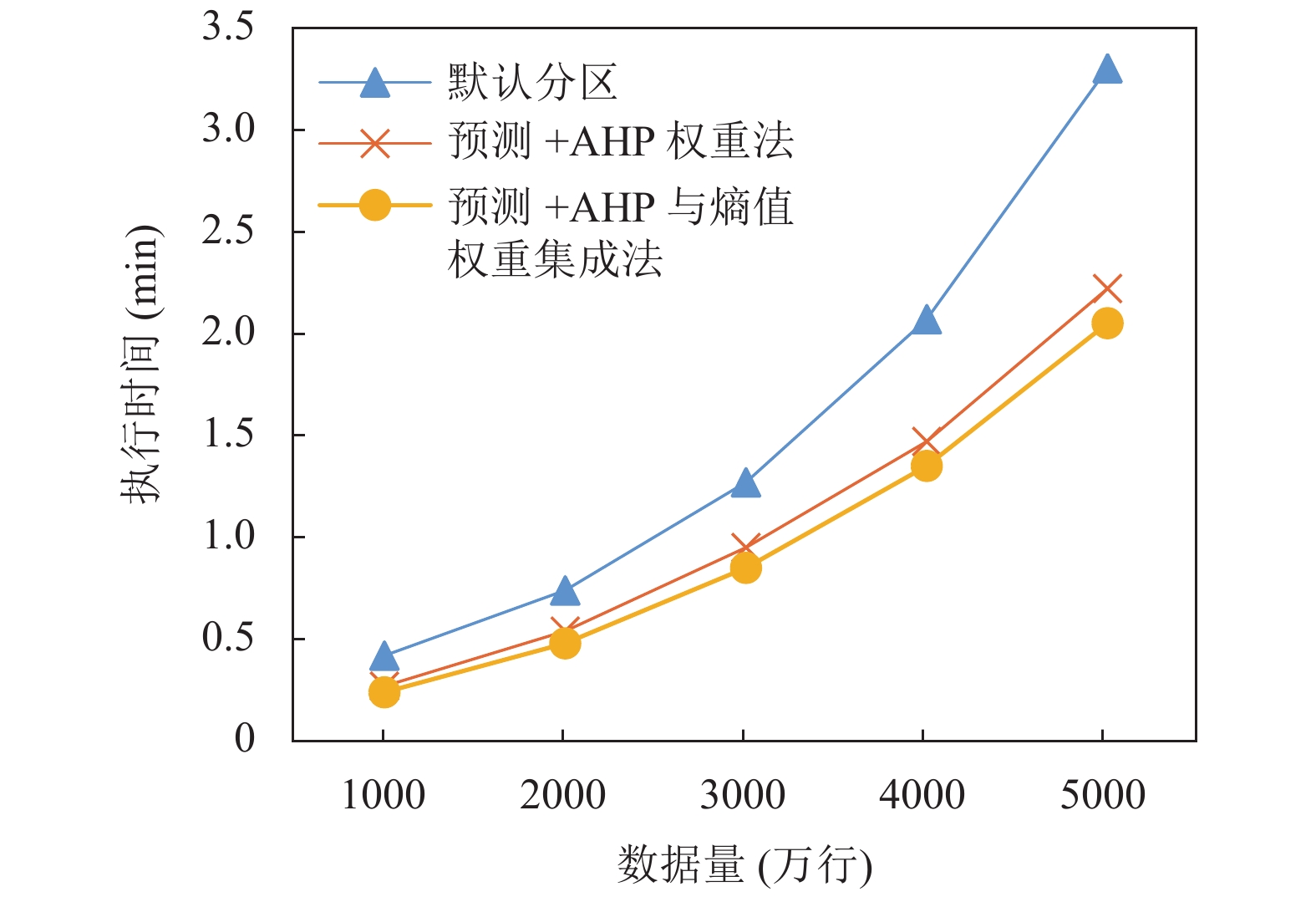
|
图 6 关联分析应用预分区策略性能对比图 |
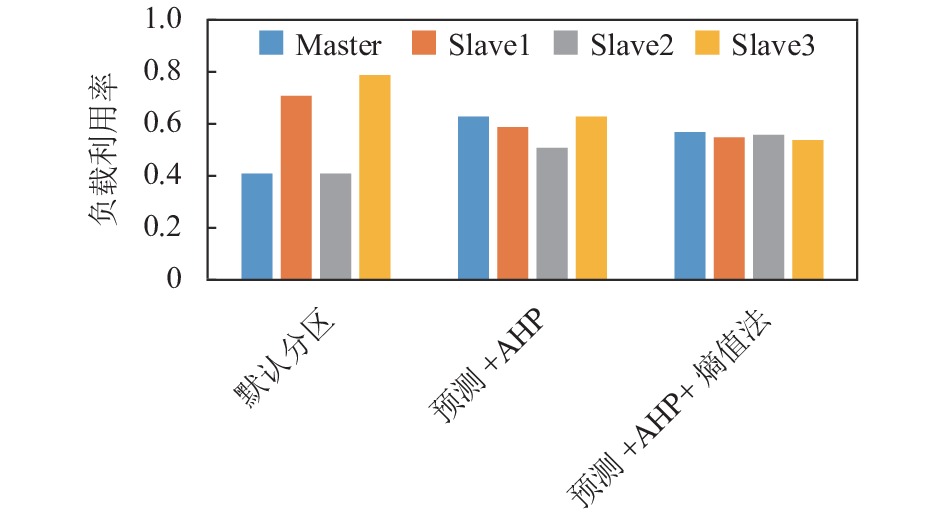
如图8、图9所示, 针对不同预分区策略执行相同的应用, 计算整个应用过程中每个节点平均负载利用率. 从整体上看默认分区策略出现严重的负载不均衡现象, 预测+AHP、预测+AHP+熵值权重集成法结合的预分区策略都能较好地解决集群负载问题, 实现集群负载的均衡性.
3.3.2 数据迁移对比测试在Spark-Elasticsearch框架中遇到负载不均衡现象, 通过数据迁移策略, 对迁移前后的执行时间进行对比, 并考虑迁移时间开销, 验证方案有效性.
利用迁移策略构造高低负载队列, 获得不同节点应发送或接收的分区块数, 执行迁移操作后, 每个节点的分区数如表7所示.
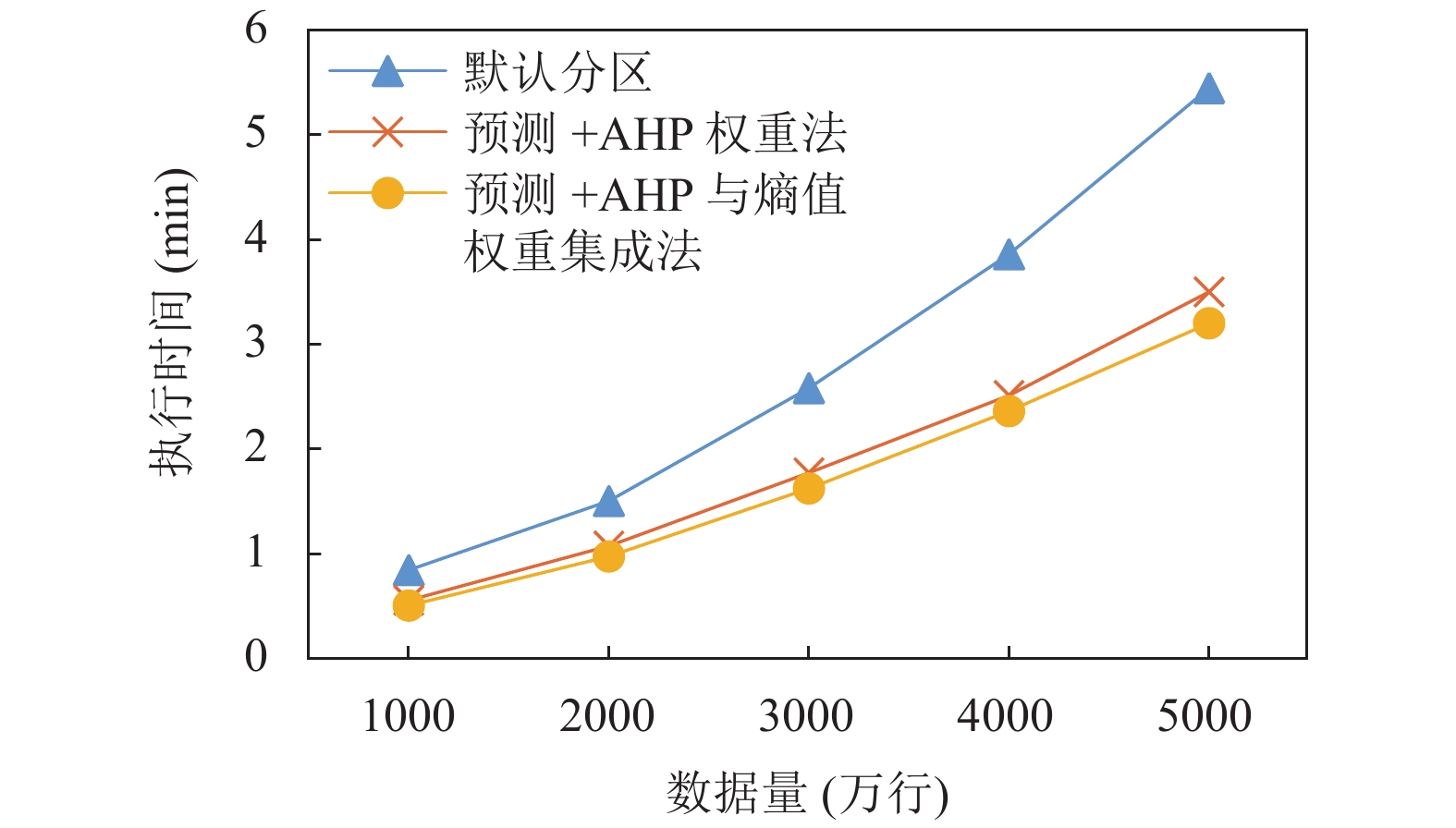
|
图 7 K-means聚类分析应用预分区策略性能对比图 |
|
图 8 关联分析应用不同预分区策略节点负载利用率对比图 |
|
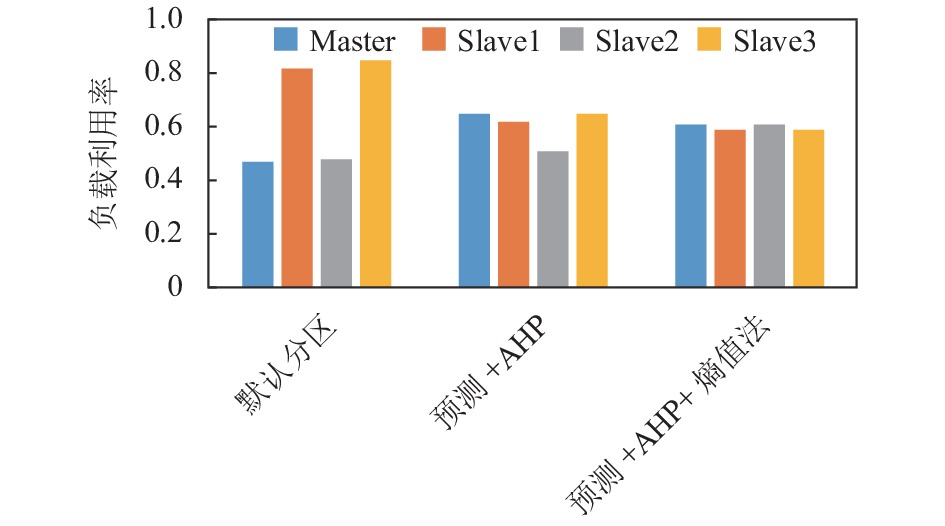
图 9 K-means聚类分析应用的不同预分区策略节点负载利用率对比图 |
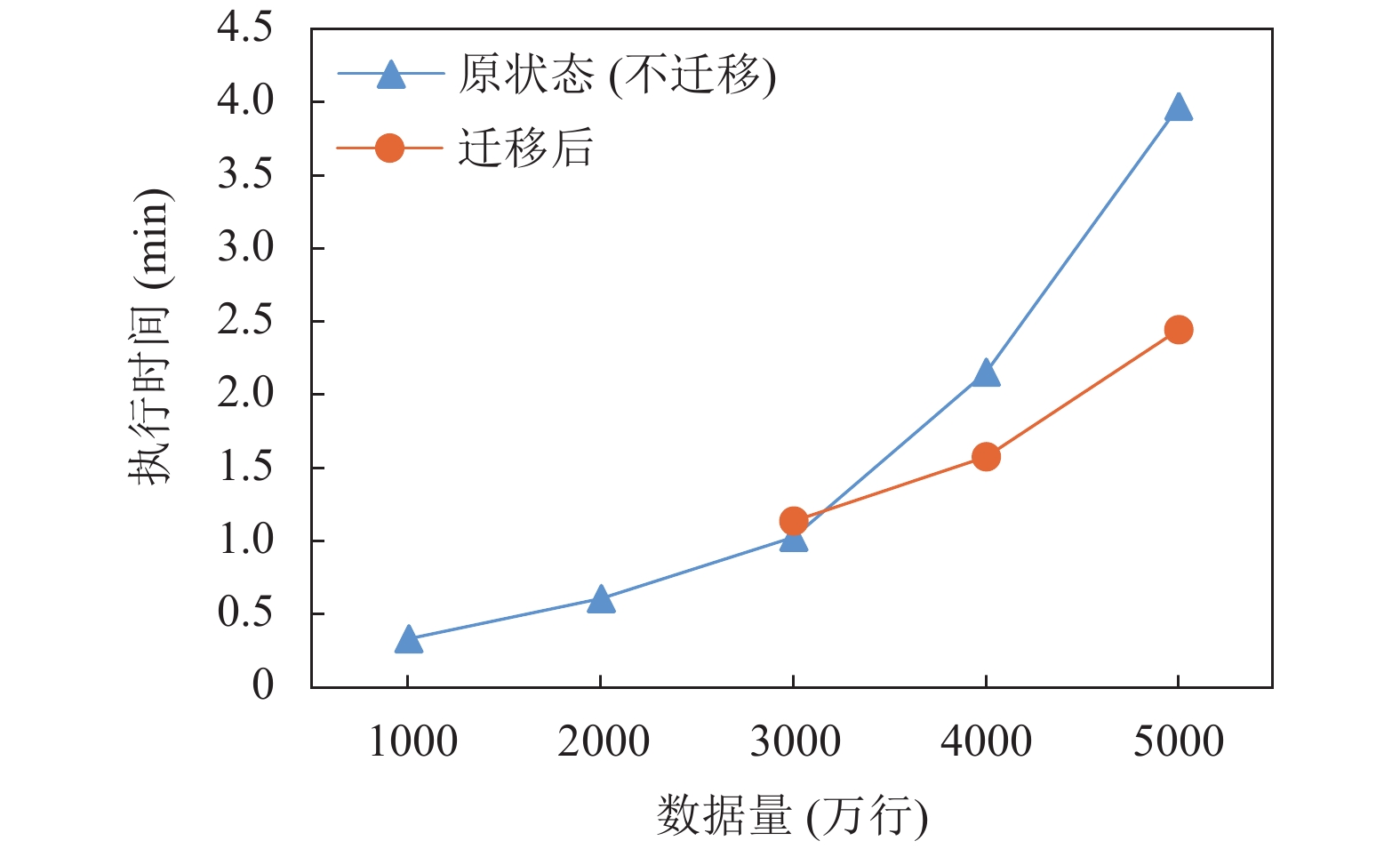
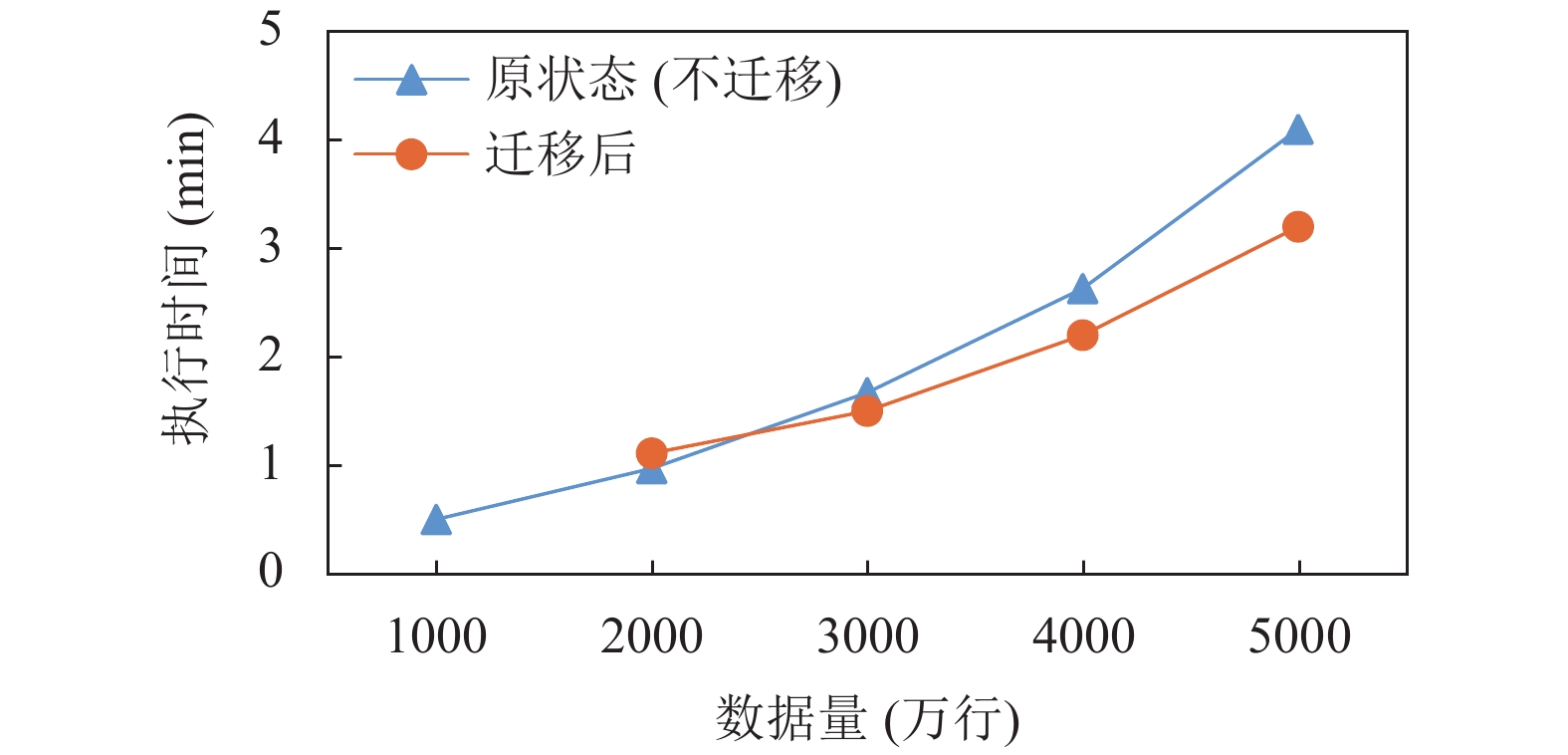
通过图10、图11所示, 表明了迁移策略的有效性, 可以改善集群的负载均衡性, 一定程度上提高了应用的响应速度. 数据量较少时, 关联分析数据量小于3000万时和K-means分析数据量小于2000万时负载没到设定的阈值, 不触发迁移, 但是当数据量相对较大时, 即关联分析数据量达到3000万和K-means分析数据量达到2000万时负载超过阈值, 触发迁移. 虽然改善了集群的负载均衡, 但是迁移需要消耗时间, 导致总时间较长, 当数据量扩大时, 负载不均衡性加剧, 导致迁移成本相对较小, 提升了应用的响应速度.
| 表 7 迁移前后的节点分区数对应表 |
|
图 10 关联分析迁移策略性能对比图 |
|
图 11 K-means聚类分析迁移策略性能对比图 |
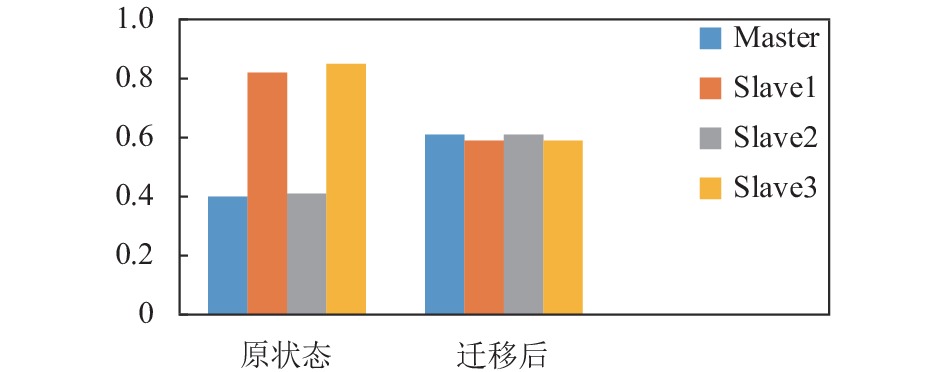
通过图12、图13所示, 对不同应用进行迁移, 比较迁移前后整个应用过程中每个节点平均负载利用率, 结果展示通过迁移能改善集群负载均衡性.

|
图 12 关联分析数据迁移前后节点负载利用率平均值对比图 |
|
图 13 K-means聚类分析数据迁移前后节点负载利用率平均值对比图 |
4 总结
本文虽然改善了集群负载均衡性, 提高了数据分析应用的响应速度, 但是依然存在一些不足之处. 日后的工作应该围绕以下几个方面进行研究:
(1)指标权重的获得
针对不同的应用难以找到最佳指标权重值, 本文采用主客观权重集成法, 能较好地避免主客观引起的偏差, 但不能得到指标权重配比最优解, 指标权重需做进一步研究及大量实验验证.
(2)数据迁移开销的理论研究
本文虽然通过数据迁移策略改善了集群负载均衡性, 但没从理论上考虑数据迁移过程中成本问题, 只是实验中包括了迁移时间.
| [1] |
Vanhove T, van Seghbroeck G, Wauters T, et al. Managing the synchronization in the Lambda architecture for optimized big data analysis. IEICE Transactions on Communications, 2016, E99-B(2): 297-306. DOI:10.1587/transcom.2015ITI0001 |
| [2] |
He ZY, Huang QL, Li ZF, et al. Handling data skew for aggregation in Spark SQL using task stealing. International Journal of Parallel Programming, 2020, 48(6): 941-956. DOI:10.1007/s10766-020-00657-z |
| [3] |
张占峰, 王文礼, 耿珊珊, 等. Spark数据倾斜问题研究. 河北省科学院学报, 2020, 37(1): 1-7. |
| [4] |
Dhulavvagol PM, Bhajantri VH, Totad SG. Performance analysis of distributed processing system using shard selection techniques on Elasticsearch. Procedia Computer Science, 2020, 167: 1626-1635. DOI:10.1016/j.procs.2020.03.373 |
| [5] |
黄秋兰, 程耀东, 陈刚. 分布式存储系统的哈希算法研究. 计算机工程与应用, 2014, 50(1): 1-4, 77. DOI:10.3778/j.issn.1002-8331.1306-0307 |
| [6] |
Li Y, Jiang YY, Gu J, et al. A cloud-based framework for large-scale log mining through Apache Spark and Elasticsearch. Applied Sciences, 2019, 9(6): 1114. DOI:10.3390/app9061114 |
| [7] |
王新友, 杨昆瓒. 基于二次平滑指数的引航事故预测研究. 中国水运, 2017, 38(9): 56-57. |
| [8] |
李想. 分布式数据库数据分配策略研究[硕士学位论文]. 大连: 大连理工大学, 2009. 5–7.
|
| [9] |
王晓燕, 陈晋川, 郭小燕, 等. 基于Nash-Pareto策略的自动数据分布方法及支持工具. 计算机研究与发展, 2015, 52(9): 1965-1975. DOI:10.7544/issn1000-1239.2015.20140832 |
| [10] |
杨华芬. 云存储环境下大数据实时动态迁移算法研究. 机械设计与制造工程, 2021, 50(2): 117-122. DOI:10.3969/j.issn.2095-509X.2021.02.025 |
| [11] |
刘琨. 云计算负载均衡策略的研究[博士学位论文]. 长春: 吉林大学, 2016. 85–110.
|
| [12] |
陈涛, 肖侬, 刘芳, 等. 基于聚类和一致Hash的数据布局算法. 软件学报, 2010, 21(12): 3175-3185. |
| [13] |
宋怀明, 安明远, 王洋, 等. 大规模数据密集型系统中的去重查询优化. 计算机研究与发展, 2010, 47(4): 581-588. |
| [14] |
王晶, 何利力. 基于虚拟机动态迁移的负载均衡策略. 计算机系统应用, 2020, 29(5): 167-174. DOI:10.3969/j.issn.1003-3254.2020.05.024 |
 2021, Vol. 30
2021, Vol. 30


